一种基于微分代数的任意阶空间目标轨道传播方法及其分析*

高 凯，潘金波，贾世伟，张宇琛，沈俊逸

(上海机电工程研究所·上海·201109)

0 引 言

弹道导弹飞行的中段将释放弹头、干扰机和诱饵；在再入段，弹头和诱饵将高速再入。雷达探测弹头时，经过多目标关联识别和干扰机对抗，真实弹头回波依然可能会淹没在噪声下。这时需要对弱信号进行长时间积累，以期达到早发现的目的。弱信号的长时间积累依赖精确的目标动力学模型及其运动状态外推。动力学模型通常用非线性微分方程来表示。而目标运动状态外推由于动力学模型的复杂性一般都没有解析解，故外推通常采用数值积分方法。随着现代计算机的发展，数值积分方法精确求解高阶非线性微分方程变得工程可行。

数值积分方法通常分为单步方法和多步方法。单步方法利用初始状态求解不同时刻不同运动状态下微分方程的值，组合这些值即可获得单步目标轨道传播，典型的方法为龙格-库塔(Runge-Kutta，RK)方法。多步方法通过组合目标的多个后向状态(即除了初始状态，还需要初始状态时刻之前时刻的状态)实现目标轨道传播，常用方法有亚当斯-巴什福斯-莫尔顿(Adams-Bashforth-Moulton) 方法和尚平-戈登(Shampine-Gordon)方法。单步方法相比多步方法不需要目标状态的后向值。多步方法通常采用单步方法来起步，但要注意阶次的匹配。很多情况下，四阶龙格-库塔方法(RK4)的精度是足够的，但在需要高阶多摄动模型时，则需要更高阶的数值积分方法，以保证积分的精度、削弱步进选择带来的精度和计算时间复杂度的影响。高阶龙格-库塔方法需要求解复杂的条件方程以获得参数表，使其在需要高阶场景下的应用变得复杂。

微分代数(Differential Algebra，DA)提供了一种使用现代计算机求解函数导数的方法。最早涉足微分代数方法的是Joseph Liouville，他将函数积分和有限项微分方程组联系在一起。之后Joseph Fels Ritt给出了求微分方程组解的完整代数理论，使微分代数方法获得了显著的进步。Ellis Robert Kolchin和Robert Henry Risch在算法方面推进了微分代数方法的发展。当前另外两种计算机求导方法分别是有限差分方法和符号计算方法。有限差分方法的缺点主要是差分间隔很难取得合适和存在无法准确获得导数值的固有缺陷。在高维空间和高阶偏导求解时，有限差分方法的时间复杂度非常高。符号计算求导方法可以和微分代数方法一样获得准确的导数值，但是该方法在处理复杂表达式求导时会难以化简表达式，导致计算机内存紧张，并且时间复杂度变得极高。这两种方法的固有特点使得它们难以在大规模复杂表达式求导过程中应用。本文将重点关注微分代数技术在求解微分方程和偏微分方程中的应用，特别是初始条件已知时流微分方程的泰勒展开。

本文给出了一种基于微分代数的任意阶空间目标轨道传播方法。该方法不需要改变外推算法的计算过程，并避免了求解复杂条件方程。文中仿真分析采用空间目标的二体运动模型(该模型可求解析解，方便分析比较)，对轨道传播方法进行分析。本文分析了步进时间和阶次对空间轨道传播精度的影响，并对高阶微分代数方法和龙格-库塔方法的精度进行了比较。

1 理论基础

微分代数通过将实数代数变量替换为微分代数变量，使函数最终计算获得的微分代数变量值包含函数对自变量的各阶微分。微分代数支持所有实数代数的运算。对如下函数关系

()=((),)

(1)

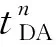
(2)

(,)+(,)=(+,+)

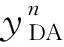
(3)

×(,)=(×,×)

(4)

(,)·(,)=(·,·+·)

(5)

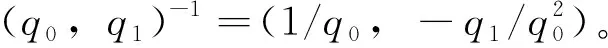
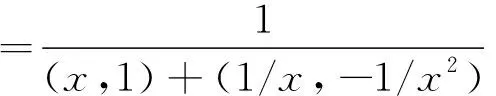
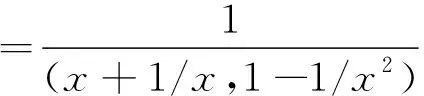
(6)

式(6)通过微分代数完成了导数的求解。当在一开始代入值计算时，可避免符号计算方法中复杂符号式子的存储、化简和计算。高阶和多变量微分代数可通过扩展上述一元一阶截断泰勒展开表达式微分代数(式(3)～式(6))来获得。

微分代数的详细计算机代码实现主要有源代码转换方法、操作符重载方法和表达式模板方法。源代码转换方法首先使用计算机代码实现目标函数，然后用预处理器按照微分法则生成新的求函数导数的代码。源代码转换方法仅能利用在代码编译时已知的信息，难以处理像循环、C++ 模板和其他面向对象特性。操作符重载的核心思想是引入新的类对象，表达微分链式法则上的微分中间量，其缺点是难以完整地表示中间变量。而类模板方法则可以解决这一问题。类模板可以返回表达式模板，在编译阶段直接通过编译器获得计算导数链式法则层次结构，并对中间变量自动形成合适的类对象。

2 空间目标轨道任意阶导数求解

2.1 空间目标动力学模型

空间目标轨道传播数值积分方法通常采用空间目标动力学方程的考埃尔形式，这是由于该形式可以很容易地添加任意摄动加速度模型。考埃尔形式如下

(7)

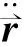
2.2 任意阶导数求解

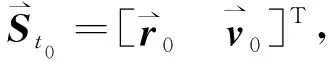
(8)

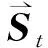
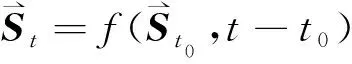
(9)

(10)

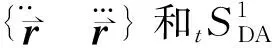
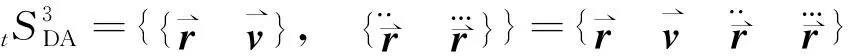
(11)

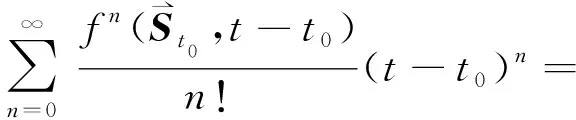
(12)

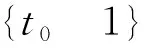
(13)

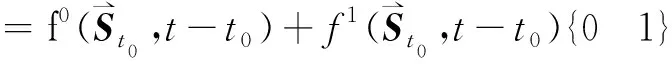
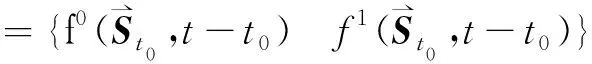
(14)

3 仿真分析

采用数值积分方法和二体运动解析解比较的方法进行仿真。将二体运动解析解作为空间目标二体运动的精确解，便于向数值积分方法提供精度参考。仿真采用的空间目标在地心惯性系(Earth-Centered Inertial，ECI)中的初始状态如表 1所示。采用精度衰减因子(Position Dilution of Precision，PDOP)来量化和比较数值积分方法的解和二体运动解析解之间的差异。

(15)

式中，(=,,)为时刻数值积分方法获得位置矢量与二体运动解析解位置矢量在方向上的差值。

表1 空间目标在地心惯性系下的状态

首先,运用微分代数方法对空间目标初始状态进行外推，外推时间为100.0s。仿真时依次获得更高阶导数，求积分后获得外推状态，之后与二体运动解析解进行比较。图1给出了随微分代数阶次的变化情况，可以看出,随微分代数阶次近似以指数形式衰减，这符合从泰勒展开式中获得的预期结果。图1中，以分贝形式给出(=10×log())。需要指出的是，在求解高阶导数时,需要采用高精度数据类型,以应对函数导数大的动态范围。

图1 σPDOP随微分代数阶次的变化Fig.1 σPDOP changes with the order of differential algebra

图2给出了满足<1时的最大轨道外推时间随微分代数阶次的变化情况。首先，通过仿真求解最大轨道外推时间对应阶次的导数，然后将上一阶次求得的最大轨道外推时间乘以2(为迭代次数)，直至≥1，记录此时的和-1对应的时刻，在和-1对应的时刻间隔内用二分法查找=1的值。由图2可以看出，满足<1的最大轨道外推时间随微分代数阶次近似以指数形式增长，这符合从泰勒展开式中获得的预期结果。图3给出了分别用龙格-库塔方法和本文所提的微分代数方法对二体运动数值积分与其解析解的比较曲线，可以看出，高阶方法在大时间步进时可有效提高外推精度。

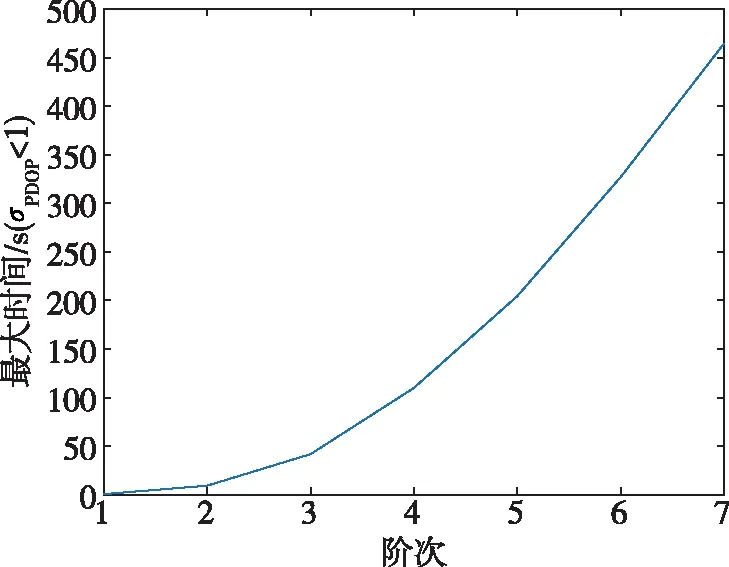
图2 满足σPDOP<1的最大轨道外推时间随微分代数阶次的变化Fig.2 Changes of the maximum orbit propagation time that satisfies σPDOP<1 with the order of differential algebra

图3 微分代数方法与龙格-库塔方法的比较Fig.3 Comparison of differential algebraic method and Runge-Kutta method

4 结 论

本文给出了一种基于微分代数的解决轨道传播问题的单步数值积分方法。该方法可在摄动力模型解析区间内给出空间目标状态对时间的任意阶导数，进而利用泰勒展开式进行轨道传播。本文在二体模型下进行仿真分析，给出了随微分代数阶次的变化情况和满足<1时的最大轨道外推时间随微分代数阶次的变化情况，并验证了方法的有效性。本文还给出了龙格-库塔方法和微分代数方法的外推精度比较，初步讨论了算法性能。