教师教学能力对学生学业成就增值的影响机制
——基于我国东西部两省调研数据的实证分析
王碧梅
一、问题提出
教师教学能力是衡量教育质量高低的核心指标,也是提高教育质量的关键要素。评判教师教学能力高低最为直接的观测指标便是学生的学业成就。通过学生学业成就的高低能够间接地对教师的教学能力做出较为客观的评价。但是,学生学业成就的影响因素有很多,比如家庭经济状况、父母受教育水平、父母职业、学生所处的学校、学生的人格特质、学习风格等。因此,仅以学生学业成就高低来评价教师的教学能力水平有失偏颇。针对这一不足,近几年新兴的一种教师评价方法——增值性评价,能够用于评价教师教学能力高低与学生学业成就的增长情况。增值性评价主要用于确定教师的贡献率和学生学业成绩增长的关系[1]。该方法不同于以往的评价方法,它采用可计算的、多因素的、复杂的增值模型,将影响教师教学效果的变量和影响学生学业成就的变量联系起来,通过建立多元线性增值模型排除影响学生学业成就的无关变量,进而推导计算出教师的教学对学生学业成就增值的“净效应值”,以此对教师的教学能力做出相对客观、公正、科学、严谨的评价。可知,增值性评价能够用于评价教师教学能力对学生学业成就的贡献率。
科学素养是中国学生发展核心素养的关键要素,也是国家综合竞争力提升的关键指标。科学素养提升的途径很多,学校科学学科教育是最为主要的途径,但科学学科在基础教育阶段存在发展不均衡的现象,尤其在东部和西部地区差异较大,进而会影响到两个地区学生的科学素养。科学素养是学生核心素养的必备素养,目前关于科学素养的测评主要以国际上三大测评项目(PISA、TIMSS和NAEP)为主,而在学校日常教学中,较为常用的测评方式是学生的学业成就测试。学生的学业成就测试能够直接反映学生的科学素养水平,具有很好的本土参考性。前期关于科学学业成就影响因素的大量研究都只在教师和学生层面上展开探讨,忽略了地区、学校的差异。因而,从地区、学校层级方面入手,分析教师教学能力对学生学业成就增值的影响十分必要。基于此,研究采用增值性评价方式,将东西部两个地区部分学生的科学学业成就水平作为因变量,将学生上一学期科学期末成绩作为协变量,建立多元线性模型,分析教师的特征变量对学生学业成就的增值情况,并探讨教师教学能力对学生学业成就增值的影响。
二、研究方法
(一)研究样本
研究主要探讨教师教学能力对学生学业成就增值的影响,因而在研究样本的选取上,采用固定抽样的方式,选取东部Z省HZ市15所学校的33位五年级科学教师和西部S省XA市18所学校的31位五年级科学教师以及这64位教师任教班级的2 827位学生作为研究样本,其中HZ市的学生人数为1 320人,XA市的学生人数为1 507人。学生的平均年龄约为11岁。
(二)研究方法
研究采用增值性评价的方法,将自变量和协变量链接起来,建立一个两水平(教师水平和学生水平)模型,严格控制始评价(前测值)时的学生水平变量与协变量以及教师水平变量的影响,以此分析不同变量对学生终评价(后测值)时学业成就增长的解释程度。在两水平模型分析的基础上,依次增加各种变量,建立多水平线性模型,通过分析结果,筛选出相关的变量建立最终增值模型,进一步分析教师变量对学生学业成就的增值情况。
(三)数据来源及分析
数据来源于:学业成就测验成绩、期末成绩、教师课堂观察量表和学生评教量表中教师变量和学生变量。其中学业成就测验量表、教师课堂观察量表、学生评教量表使用王碧梅博士在《小学科学教师课堂教学能力评价》一文中编制的量表。三个量表的信度值分别为0.883、0.900、0.901,且结构效度、内容效度良好,能用于相关内容的测评。学生的期末成绩选用评价前上一学期的成绩,成绩由学校教务处统一提供。
数据处理使用Mplus7和SPSS16.0软件进行。具体处理方式如下:
1.建立数据库
通过分数转换、垂直等值的方式将学生两次成绩相链接,并建立起教师特征变量、学生特征变量和学业成绩的数据库。
2.多水平线性模型建立
模型一:建立零模型。首先需要以学生的科学学业成就测试成绩作为模型的因变量,以学生为第一水平,以教师为第二水平,建立一个两水平零模型。在零模型中,没有自变量,旨在考查学生水平和教师水平在学生学业成就差异上的变异情况。模型为:
第一层:Yij= βij+ eij
第二层:β0j= γ00+ μ0j
模型二:建立基础增值模型。该模型在零模型的基础上加入一个解释变量,旨在考查教师水平的变异情况。通过模型建立能够初步判断出对学生学业成就测试有显著性影响的变量,也能够判断出学生水平上的自变量在教师水平上是否有显著性差异。
第一层:Yij= β0j+ β1jXij+ eij
第二层:β0j= γ00+ μ0j
β1j= γ10
模型三:建立随机效应协方差分析模型。该模型需要在基础增值模型的学生水平层面上加入解释变量,旨在分析学生的变量对其学业成就的影响。
第一层:Yij= β0j+ β1jXij+ β2jZij+ eij
第二层:β0j= γ00+ μ0j
β1j= γ10
β2j= γ20
模型四:建立随机系数模型。该模型需要在基础增值模型的教师层面上加入教师的解释变量,旨在分析教师变量对学生学业成就的影响。并将有显著性效应的变量加入到模型三中,旨在分析教师水平变量与学生水平变量的交互作用对学生学业成就的影响。
第一层:Yij= β0j+ β1jXij+ eij
第二层:β0j= γ00+ μ0j
β1j= γ10+ μ1j
模型五:建立最终完整增值模型。该模型需要在模型二的基础上,加入教师水平变量、学生水平变量以及交互作用的变量,旨在考查影响学生学业成就的最终因素。
第一层:Yij= β0j+ β1jXij+ β2jZij+ eij
第二层:β0j+ γ00+ γ01W01j+ μ0j
β1j= γ10+ γ11W11j
β2j= γ20+ γ21W21j
3.修正得分
根据增值情况和部分质性材料的分析修正最终得分。
三、结果分析
(一)学生科学学业成就增长情况分析
为了更好地计算学生学业成就的增长情况,研究需要对学生的两次学业成绩得分进行等值换算。由于两次测试的班级是固定的,班级人数也是固定的,班级平均分大致相似,使用的测试卷也属于平行试卷,测验的难度、区分度相似,测验所得分数X和Y的信度相等,所以可以使用线性等值的方式对原始分数进行处理。
(二)学生水平变量对学业成就的影响因素分析
学生的性别、年龄、家庭经济情况、所处学校层级等因素都能够影响学业成就的增长情况。为了更好地确定出教师教学能力对学业成就增值的“净效应值”,研究需要对这些因素进行排除。需要建立一个以学生水平为第一层,以教师水平为第二层的两水平模型,以此初步判断出两个水平在学业成就测验上的变异程度,结果如表1。

表1.第一个模型分析结果
在两水平的模型中,学生的学业成就变异在教师间(Z = 3.091,p = 0.001)和教师内(Z = 53.982,p = 0.000)存在显著性差异。说明不同的教师对学生的学业成就存在显著性影响;教师的个体特征变量也对学生的学业成就有显著性差异。通过计算得出跨级相关系数为18.81%,说明在学生的学业成绩总变异中由教师层所引起的变异是18.81%。因此,需要建立第二个模型。
为了能够分析学业成就差异受哪些变量的影响,研究在零模型的基础上,增加了一个解释变量,学生的期末成就,以此去检验教师水平对学生学业成就的变异情况。模型分析结果如表2。
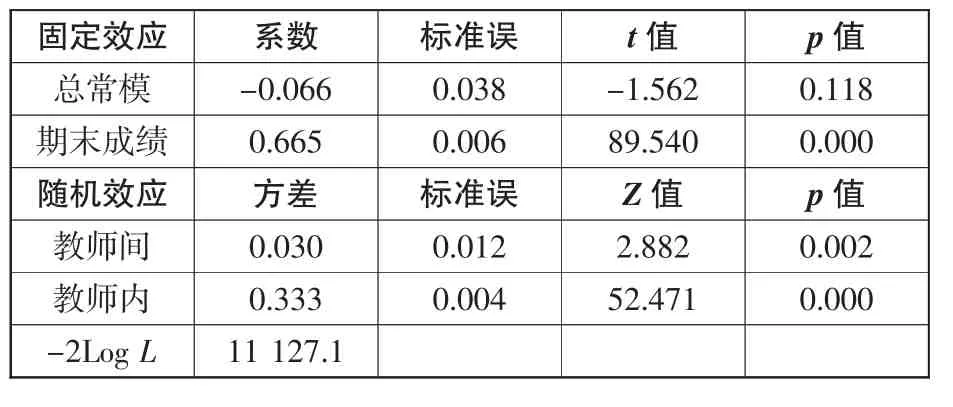
表2.第二个模型分析结果
以学生期末成绩为解释变量加入模型中,发现教师间和教师内的变异情况相对于零模型的变异情况有所下降,教师间变异下降了48.75%,教师内变异下降了45.68%,但是教师间和教师内仍存在显著性差异。为弄清教师水平变量对学生学业成就变异的影响,排除学生自身变量带来的差异,研究在学生水平层面上增加了一个解释变量,以此去分析学生的哪些变量影响了其自身的学业成就增值情况。增加的解释变量为学生水平的特征变量,加入规则是依次加入,分析结果如表3。

表3.学生水平增值模型分析结果
表3可知,学生的特征变量性别(b = 0.071,p =0.000)、家庭经济情况(b = -1.040,p = 0.047)、父母职业(b = -0.511,p = 0.045)三个变量有显著性效应,而年龄(b = 1.131,p = 0.175)无显著性差异。为厘清内部差异,研究采用回归方程系数进行检验,结果显示:在性别变量上,男生的增值优于女生;在家庭经济变量上,家庭经济殷实的学生增值比经济略微单薄的学生增值快;在父母职业上,事业单位、公务员、商人等家庭子女比工人、小商贩、无业等的家庭子女增值要明显。但这三种特征变量在教师水平变量上是否存在随机变异情况,就需要建立模型检验。通过建立随机系数模型可知,学生学业成就在教师变量和学生性别变量上是随机变异的,在家庭经济情况、父母职业两个变量上的变异情况是固定的。也就是说,学生的家庭经济情况、父母职业对学生学业成就的影响是一致的,与教师变量无关。然而,学生的性别对学业成就的影响就与教师变量有关。
(三)教师水平变量对学业成就的影响因素分析
为了检验教师的哪些变量影响了学生的学业成就,研究需要在教师层面上依次加入教师的解释变量,建立增值模型。分析结果如表4所示。
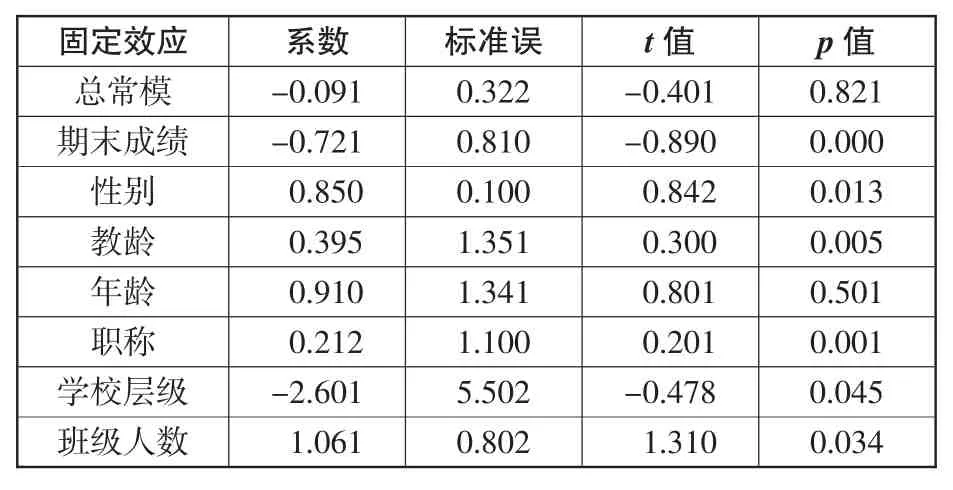
表4.教师水平增值模型分析结果
结果显示:教师的性别(b = 0.850,p = 0.013)、教龄(b=0.395,p=0.005)、职称(b=0.212,p=0.001)、所处学校层级(b = -2.601,p = 0.045)、任教班级人数(b = 1.061,p = 0.034)均对学生的科学学业成就测试成绩具有显著效应,但教师的年龄(b = 0.910,p = 0.501)无显著效应。通过回归方程系数分析发现:性别维度上,男性教师的增值优于女性教师;教龄维度上,6-10年教龄段教师的增值比其他三个阶段的教师增值好;职称维度上,高级职称教师的增值比初级职称教师的增值要好;学校层级维度上,重点学校教师的增值优于一般学校的教师;班级人数维度上,班级人数较少的任课教师的增值优于班级人数较多的任课教师的增值。
(四)两类水平变量的交互作用对学业成就的影响因素分析
为探寻学生学业成就增长中教师变量和学生变量之间的交互作用,研究建立了两水平交互作用模型,将教师变量中的性别、教龄、职称、所处学校层级、任教班级人数加入到学生变量的随机效应协方差分析模型中检验,结果如表5所示。
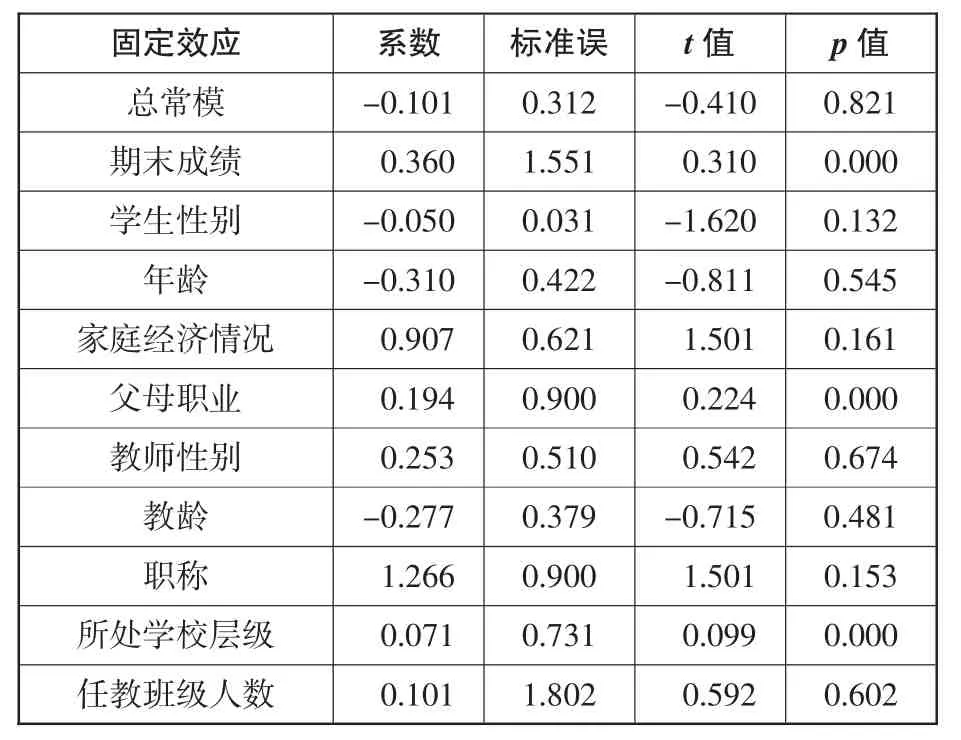
表5.两类水平变量的交互作用模型分析结果
从交互作用模型结果中可知,教师变量与学生变量中只有学生父母职业和学生所处层级之间有交互作用,其余均无交互作用。也就是说,父母职业和学生所处学校层级之间的交互作用对学生的学业成就也会存在影响。故在完整模型的建立中,需要将这个交互作用考虑在内。
(五)完整模型的因素分析
通过上述多个水平模型的建立,研究将无显著效应的变量进行删除,仅将有显著性效应的变量放入完整模型中检验,结果如表6。

表6.完整模型分析结果
在完整模型中,对学生的学业成就有显著性效应的变量有:教师的性别、教龄、职称、所处学校层级、任教班级人数。其余的无显著效应。此外,完整模型相对于第一个模型而言,教师任教班级之间学生学业成绩的变异下降了60.12%。
为求出学生增值的“净效应”值,研究采用残差计算教师效应的大小。通过完整模型的残差计算得到64位科学教师效应的大小,如图1所示。
从残差图可知,在调查的64位教师中28位教师对学生的学业成就是负增值,17位教师对学生的学业成就是正增值。其余教师的增值效应无统计学上的意义。
四、结果讨论
(一)教师个人特征对学生学业成就的影响:学科特质的作用
教师的个人特征在研究中主要指教师的性别因素。性别作为人口学变量的特征之一,常被引用到教育问题的探讨中,尤其在特定学科的教学质量中。大量的研究指出,“女性教师和男性教师有不同的学术产出,尤其对女学生在数学和科学领域上的表现。”[2][3][4][5]进一步说,“女性教师的教学不利于女学生科学学业成就的提高,会使女学生的科学成绩比男学生差[6][7]。该观点在本研究中也得到了确认。增值模型的数据显示,教师性别对学生学业成就也有着显著差异。探究差异的根源,需要回到学科本身的性别特质讨论该问题。
科学是一门注重逻辑推理的学科,该学科有着极强的男性特质。它旨在通过各类核心概念的理解、大概念的整合,通过实验探究、动手操作、推理论证等培养学生的科学核心素养。该门课程的知识以逻辑推理为主,极为强调数据的重要性、实验研究的可重复性、实验数据的可验证性等。这种知识体系和学科培养目的都与社会建构起来的男性特质相似,并且在“教育教学实践”中被反复确认和认证。如通过对课堂教学观察分析发现,男性教师更关注实验的过程和数据的精准性,实验设计的合理性;女性教师更关注在实验中培养学生的情感、态度,如热爱自然、团结合作等。而科学学科的知识特性和学科目的是以培养学生的实验设计、实验操作、推理论证等核心素养为主。男性教师和女性教师在教学过程中的差异,必然会影响教学目标设定的差异,并因此影响到学生习得内容的差异,进而影响学生的学业成就。
(二)教师的职称和教龄对学生学业成就的影响:符号资本的映射作用
在中小学校,教师的“职称评定直接与教师的教学质量和经验挂钩,职称较高的教师往往具有丰富的教学经验,职称较低的教师往往是较为年轻的教师,缺乏一定的经验”[8]。经验、教学质量就成为教师能力显现的符号资本,进而运作于教师的教育教学实践过程中,成为教师的职称评定与能力甄别的分类原则。在学校场域内,教师的资本类型主要表现为文化资本,具体可分为文化能力、文化产品、文化制度三种形式。
文化能力是教师必备的资本类型之一,每位教师都具备,但并不等同。新手教师和专家教师其文化能力会有很大差异,这种差异体现在教学过程中,以“师定知识”为主,并最终影响到学生的学业成就。而这种能力的积累需要以教学经验的不断丰富为必要条件,故教师的教龄会影响到其文化能力的状态,进而影响到学生的学业成就。文化产品是教师在教学实践中不断积累起来的一种资本类型,它是一种“客观的状态,以文化商品的形式”存在,如教师的教学风格、教学模式、教学理念等。这些风格、模式、理念在长期的教育教学实践之中被提升、验证,不仅能作用于教师自身的教学,也被群体内的教师所认可和接受,并有可能成为“引领示范”的“模范”。这种资本并非每位教师都具备,它不仅需要教师丰富的教学经验,还需要教师具备相应的能力、理念、风格等,且上述要素还需要在各种教学大赛、公开课、观摩课等与教学相关的活动中彰显,以使资本外化为一种客观的形式。客观化的形式会再制约教师的教学实践,进而影响学生的学业成就。文化制度是一种“体制的状态,其赋予文化资本一种完全是原始性的财产”[9]。作为体制状态存在的资本,在科学教学领域内具有绝对的话语权,而它的积累不仅需要丰富的教学经验,还需要职称系列的“顶端性”,因为职称在教师系列中是一种符号资本,具有象征权力。在其象征权力中,最为直接的便是教师的教学能力差异。而在本次调查的对象中,为了满足样本的多样性,且验证教师职称对学生学业成就的影响,研究选取了不同教龄段的教师,通过线性模型分析可知,在学生的学业成就增值中,教师的教龄和职称也起着显著性的作用。教龄和职称在教师特征中,是以不同的文化资本类型和数量来区分教师的教学能力,并在教学实践中影响到学生学业成就。
(三)学生就读学校层级对其学业成就的影响:资源与规则的互构
学校层级的差异除去师生的差异外,主要体现在资源和规则的差异上。学校的资源有两种类型[10]98:配置性资源和权威性资源。这两类资源都是学校场域内行动者实践的逻辑体系。具体表现为:在每个相对独立的学校场域内,行动者所生产出来的“符号产品”,都可以从自己所拥有的资本类型和数量上占据场域内的位置,并建构相关的社会结构关系。在功能性构成要素上,由于资本类型与数量的差异,重点学校的资源比一般学校的资源更为丰富。虽然学校场域内主要以文化资本为主,但是文化产品和文化制度主要集中于重点学校,且在数量上占有优势。由此,在特定场域内被认可和追随的教学模式、教育理念等大多都源于重点学校。以一种制度性或者官方化的存在隐匿于科学教育教学场域内,不仅影响着该场域内行动者的实践逻辑,也影响着其他相似场域内行动者的实践逻辑。正是在资本的运作中,学校通过资本建构场域内的位置关系,又通过自身所处的位置关系再次建构资本的类型和数量,以此实现地位的再生产。
学校中所指涉的规则有表意性规则、合法化规则和支配性规则。表意性规则主要表现在解释和沟通上,合法化规则主要表现在规范和约束上,支配性规则主要表现在手段和权力上。规则的表现形式对应着行动者的实践逻辑,这种实践逻辑又与资源密切相关。重点学校在支配性规则上拥有至高的话语权,他们能够充分利用规则获取资源,也能够利用资源获得规则的把控权,进而决定着场域内行动者的实践逻辑。规则和资源二者是相互交织的。资源能够再制规则,规则也能够再制资源。在学校这个特殊的场域内,只有将资源和规则耦合在一起,才能更好地理解行动者的实践逻辑。如在职称评定中,重点学校凭借自身的资源,能够较多地参与规则的制定,规则制定的行动者多数从自身权力和权利的权衡进行行动,以此为“自己”服务。在学校场域内,重点学校处于支配地位,“其在特定的社会情境中所能掌控规则和利用资源的程度始终是较高的”[10]99。也就是说,学校层级结构决定了资源的占有和规则的掌控,规则的掌控和资源的占有又决定了学校的层级结构。学校是资源和规则再制的系统。而学校的资源和规则差异,会作用于师资力量和生源结构的差异,进而成为学生学业成就的影响因素。
五、总结
学生学业成就增值受多方面因素的影响,其中教师的性别、教龄、职称、学生就读学校的层级是外在因素。在本研究中,社会分工规约了男性和女性的职业就业取向,型塑了他们的社会性别意识。型塑的方式便是课程内容与教学实践。科学是一门极具男性色彩的学科,其学科属性、学科思维都与男性特质相似,故男性教师和女性教师在科学学科的产出上会有所差异,进而会影响到学生的学业成就。学校的资本类型以文化资本为主,文化资本以教学能力的形式外显于教师的教育教学实践,并作为分类原则影响到教师的职称定级。不同的文化资本占有者,其资本类型和数量上是有差异的。这种差异源于教师的教学经验、教学能力,作用于教师的职称定级。社会结构建构着学校层级结构,学校层级结构又再制着社会结构。这种互构的机制便是资源和规则的分配原则。资源和规则是学校组织制度的两项核心指标,但是由于资源和规则的分配不均,致使学校层级存在差异,由此影响了学校的层级结构和学生生源的阶层差异,进而影响到学生的学业成就。

