人的寿命与居住地GDP、海拔高度和森林覆盖率的伴随关系分析
温宇光, 孙红英, 朱景林, 魏宪举, 王 欢
(1. 四平市林业科学研究院, 吉林 四平 136000; 2. 四平市国有林总场, 吉林 四平 136002)
自2018年以来,全国各网站持续在发布着《2018年中国各省人均寿命》的排名表,而由此引发人们紧跟热评的文字:“从前5名和后5名看,国人平均寿命怎么是哪发达、哪医疗条件好、哪工资高,哪的人寿命就长?青藏高原天天蓝天白云,却寿命最短,说明还是与医疗条件、吃的好、喝的好有关”。针对热评中提到的吃喝重要性若延展推及,人们吸入空气中的氧气、雾霾、树木向空气中散发的精气都属于“吃喝”范畴,寿命与这些因素也应该有相关关系。本文以我国31个省(自治区、直辖市)人均寿命为因变量,以各省与医疗和饮食直接关联的人均GDP、与单位体积空气含氧量直接关联的海拔高度、与空气中树木精气含量直接关联的森林覆盖率为自变量,统计分析因变量与各个自变量的相关性。
1 数据收集
2018年各省(自治区、直辖市)人均GDP数据从国家统计局获得;森林覆盖率数据从第九次全国森林资源清查资料中获得;各地海拔高度从“百度地图”APP上查出,各省(自治区)海拔高度取各省地级市平均海拔高度。以上3个因素与对应31个省(自治区、直辖市)的人均寿命统计情况见表1。
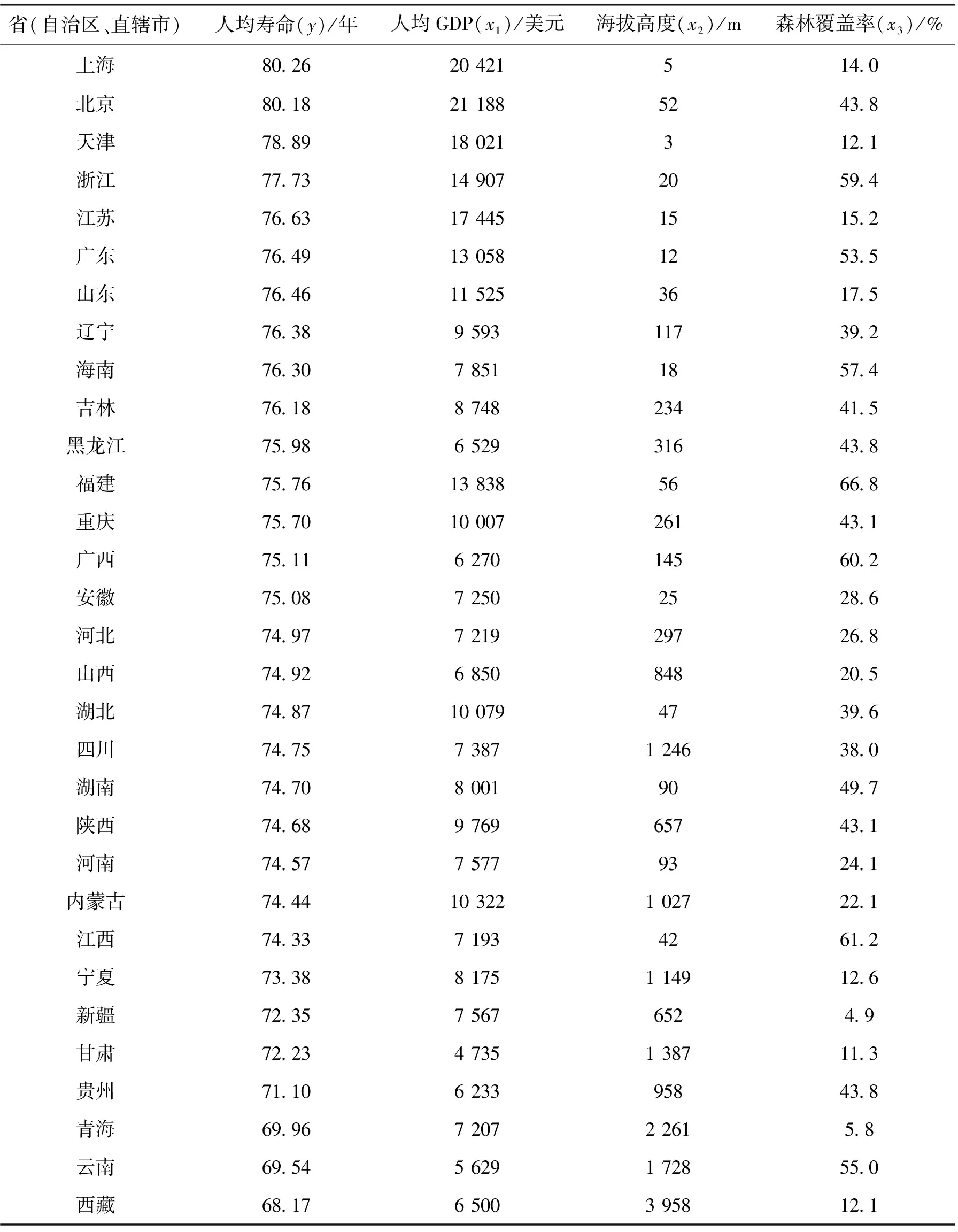
表1 2018年各省(自治区、直辖市)人均寿命、人均GDP、海拔高度及森林覆盖率
2 分析方法
以表1中我国31个省(自治区、直辖市)人均寿命为因变量,以人均GDP、海拔高度、森林覆盖率为自变量,进行多元非线性回归分析。
3 结果与分析
3.1 建立回归方程
一般来讲,上述因变量和各自变量遵循公式(1)所示的多元非线性回归方程:
(1)
将公式(1)两边取常用对数,得方程(2):
(2)

(3)
式中:A为方程(3)常数项参数;a为方程(1)常数项参数;x1为人均GDP;x2为海拔高度;x3为森林覆盖率;b1、b2、b3分别为X1、X2、X3的样本偏回归系数。
根据最小二乘法,上述参数和偏回归系数可通过如下方程组求得。

上面方程组中n=31,为省(自治区、直辖市)数量,即每个变量的样本个数。解方程组得:
A=1.697 852 184,b1=0.044 185 684,
b2=-0.010 730 403,b3=0.017 052 131。
线性方程(3)即为:

(4)
并由A=1.697 852 184得出a=10A=101.697852184=49.871 5,则非线性回归方程(1)即为:
(5)
3.2 因变量与自变量整体上相关显著性检验
公式(5)中:a=49.871 5为正数、b1=0.044 185 684为正数,说明人均寿命(y)与人均GDP(x1)成正相关;b2=-0.010 730 403为负数,说明人均寿命(y)与海拔高度(x2)成负相关;b3=0.017 052 131为正数,说明人均寿命(y)与森林覆盖率(x3)成正相关。但人均寿命与人均GDP、海拔高度、森林覆盖率的相关程度在整体上是否存在显著性,需用复相关系数检验。
根据下面公式计算得出(4)式因变量和自变量在整体上的复相关系数:
(6)
式中:rY.1,2,3为(4)式因变量与各个自变量在总体上的相关程度值,即复相关系数;Yi=logyi,yi为各省(自治区、直辖市)人均寿命;n为各省(自治区、直辖市)的数量。
通过公式(6)检验复相关系数的临界值为:
相关极显著复相关系数临界值r0.01(n-m-1)=r0.01(31-3-1)=r0.01(27)=0.471 6,其中m为自变量数。
相关极大显著复相关系数临界值r0.001(27)=0.580 1。
复相关系数与临界值比较进行显著性检验:
|rY.1,2,3|=0.936 9 > r0.01(27)=0.471 6,证明达到了极显著相关关系水平。
|rY.1,2,3|=0.936 9 > r0.001(27)=0.580 1,证明达到了极大显著相关关系水平。
从复相关系数与临界值的大小比较检验证明,一般因变量和自变量达到显著相关水平(危险率0.05),就证明回归方程精准;现在相关性超过显著水平,达到极显著水平(危险率0.01)和极大显著水平(危险率0.001),证明线性回归方程(4)高度精准,也就是方程(5)高度精准。即(5)式因变量人均寿命与人均GDP、海拔高度、森林覆盖率3个自变量整体上相关关系达到了极大显著相关水平。
3.3 因变量与各自变量的相关显著性检验
对回归方程(4)每个自变量在排除另外2个自变量的情况下,单独与因变量寿命是否存在相关显著性,需用偏相关系数检验。偏相关系数公式为:
r0j.1,2,…j-1,j+1,…m=
通过公式(7)计算得出:
人均寿命与人均GDP的偏相关系数r01.2,3=0.634 0,人均寿命与海拔高度的偏相关系数r02.1,3=-0.715 4,人均寿命与森林覆盖率的偏相关系数r03.1,2=0.601 5。
而检验偏相关系数的临界值为:
相关极显著偏相关系数临界值r0.01(n-2)=r0.01(31-2)=r0.01(29)=0.456 3,相关极大显著复相关系数临界值r0.001(29)=0.562 8。
偏相关系数与临界值比较,进行显著性检验:
人均寿命和人均GDP的偏相关系数与临界值比较,|r01.2,3|=0.634 0 > r0.01(29)=0.456 3,证明达到了极显著相关关系水平;|r01.2,3|=0.634 0 > r0.001(29)=0.562 8,证明达到了极大显著相关关系水平。
人均寿命和海拔高度的偏相关系数与临界值比较,|r02.1,3|=0.715 4 > r0.01(29)=0.456 3,证明达到了极显著相关关系水平;|r02.1,3|=0.715 4 > r0.001(29)=0.562 8,证明达到了极大显著相关关系水平。
人均寿命和森林覆盖率的偏相关系数与临界值比较,|r03.1,2|=0.601 5 > r0.01(29)=0.456 3,证明达到了极显著相关关系水平;|r03.1,2|=0.601 5 > r0.001(29)=0.562 8,证明达到了极大显著相关关系水平。
从偏相关系数与临界值的比较检验证明,因变量人均寿命与每个自变量人均GDP、海拔高度、森林覆盖率都单独具有极大的显著相关性。
4 讨论
人均寿命与人居所在地人均GDP的关系,从回归方程(5)可以看出a值为正数,人均GDP值x1的指数b1为正数;或人均寿命与人均GDP的偏相关系数r01.2,3为正数,都证明了人均寿命与人均GDP成正相关,即人均GDP越高人均寿命越长。这个规律很明显,从各省之间经济差异上可看得出;而且从时间跨度上也能直观地看出,现代人的寿命比古人普遍长,缘于与优越经济条件直接关联带来的优质饮食、舒适的居住环境、良好的医疗保障等。
同理,人均寿命与人居所在地海拔高度的关系,回归方程(5)海拔值x2的指数b2为负数;或人均寿命与海拔高度的偏相关系数r02.1,3为负数,都证明了人均寿命与海拔高度成负相关,即海拔越高人均寿命越短。因为海拔越高气压越低,造成人的吸氧量不足。以色列“高压氧疗法”就是氧气重要性的例证之一,对老年人每周5次、每次90 min身处略高于一个大气压的纯氧气舱内进行输氧试验,3个月后,生理指标发生时光倒流性的明显年轻化,延缓了衰老[1]。
人均寿命与人居所在地森林覆盖率的关系,回归方程(5)森林覆盖率x3的指数b3为正数;或人均寿命与森林覆盖率的偏相关系数r03.1,2为正数,都证明了人均寿命与森林覆盖率成正相关,即森林覆盖率越高人均寿命越长。树木对人体健康的影响在不断得到研究证明,树木的新陈代谢包括次生代谢会释放出种类繁多的对环境和人体健康有益的挥发性物质。例如松脂、丁香酸、柠檬油、树木香精油、肉桂油、单萜烯、倍半萜烯、双萜烯、负氧离子等,大多具有杀菌、抗菌、抗炎、抗癌、抗微生物、增强免疫力和减少情绪焦虑的作用,这些物质被统称为植物精气[2]。例如,人体先天形成的NK细胞(natural killer cell,即天然追杀细胞)是淋巴细胞不同类型的一种,占10 %左右,有抗病毒抗肿瘤的作用,在体内流动,通过分泌穿孔素使细胞膜破裂而摧毁病细胞。而树木会向空气中散发芬多精,吸入芬多精可使人体内NK细胞含量提高50 %左右,在树林中活动可获得极好的保健作用。瑞典科学家研究表明,居民距离绿地远近与人的健康关系密切[2]。所以,森林对保障人体健康、延长寿命的作用是直接的。在现实中,森林密布的地方居住人口往往很少,人口密集的地方却缺少森林。而林草部门森林覆盖率的计算不包括经济林、灌木林、郁闭度不超过0.2的疏林以及城乡绿化树、庭院绿化树,如果将这些树木也纳入数据分析对人口密集度做进一步分析,树木对增长寿命的正相关性会体现得更强。近年来,在国家森林城市建设标准里出现了“林木覆盖率”的概念[3],这个数据对分析与寿命的相关性最准确,但目前各地还缺少这方面数据。现在仅从森林覆盖率的数据就已经分析出了森林对人增寿的正向促进作用。仅森林对人类的巨大保健作用就说明了“绿水青山就是金山银山”重要理念的深刻性[4],也说明人居环境绿化使人更能贴近树木,对保健更为重要[5]。
基于森林对人的生理和心理双重保健作用较大,20世纪70年代发达国家开始兴起城市林业建设,现在已得到世界各地广泛认同[2]。而人们居住地的经济需要从整体上逐步发展,居住地海拔人为不能改变,唯在居住地栽树不仅容易做到,而且人人都能平等受益。因此,大力发展城市林业,建设城市森林,大力开展村屯绿化,房前屋后绿化,室内养花(木本释放的精气种类更全[2]),尽可能增加绿量,意义重大。绿化已不是简单的美化问题,而是与人的生命安全紧密相关的大问题[2]。可以看出,寿命不只是单纯与“医疗条件好、吃好、喝好”有直接关联的GDP相关,海拔、森林的作用也处于同等不可忽视的地位。
5 结论
人均寿命长短与其居住地人均GDP成正相关,与海拔高度成负相关,与森林覆盖率成正相关。但GDP需随社会经济整体逐渐增长,海拔高度难以改变,而多栽树容易做到,会紧密人与树木的共栖关系。本次研究主要是从数据角度分析相关性,不是主要研究人体与GDP、海拔高度、森林覆盖率的直接生理关联关系,所得出的寿命与各因素的相关关系,如果更严谨地表述,也可称为观察性分析、队列分析或伴随关系分析。

