基于改进Gardner算法的水下无线光OQPSK系统性能分析
杨 祎,刘 雯,阴亚芳,贺锋涛,张建磊
(西安邮电大学电子工程学院,陕西 西安 710121)
0 引言
水下无线光通信具有无电磁辐射、速率快、可移动性强、安全性好、带宽高和绿色环保等优点[1-3],所以UWOC技术在商业、政治和军事等方面都有着非常重要的作用。相较于大气光通信[4],水下光通信的光束脉冲受海水介质中吸收和散射的影响,使光信号在水下衰减严重,导致系统误码率(BER)急剧增大,最终限制了光信号在水下的传输距离[5]。
因此,探究抗干扰性能更好的调制方式对水下无线光通信系统具有十分重要的价值和意义。目前蓝绿光外调制技术实现具有一定的困难,所以强度调制-直接检测技术(IM/DD)一直是UWOC系统所采用的主要技术。其中OOK调制接收端的判断阈值设置较难,脉冲位置(PPM)调制方式易于实现,但带宽利用率不高[6]。Wang等[7]采用基于16PPM调制的UWOC系统,实现了传输距离为6 m且速率约为0.98 Mb/s的无失真传输。而采用基于正交频分复用(OFDM)的光强调制技术可充分利用光信道的带宽资源。文献[8]采用16QAM-OFDM调制实现了传输速率高达12.4 Gb/s、距离仅为1.7 m的水下无线光通信系统。但这种调制格式的系统对信道环境的理想性要求很高[8-10],而且传输距离和传输容量也存在冲突,对于长距离传输,传输能力会减少。因此,为了较好地均衡传输距离和容量,实现水下信道的传输,可采用基于MPSK/MQAM调制的直接调制技术[11,12]。其中QAM、QDPSK和OQPSK调制都是具有四相位的调制方案,相比于二相位的调制方式,可更充分地利用光信道带宽,又比更高阶的调制易于实现。因此,对比它们对水下无线光通信系统误码率性能的影响,目前OQPSK调制在自由空间光通信、光纤通信和卫星通信中都有良好的表现。Gong[13]研究了基于正交相移键控(QPSK)/OQPSK调制的自由空间光通信系统,发现采用OQPSK调制比采用QPSK调制的系统更适合长距离通信。El-Nahal等[14]研究了基于OQPSK和DPSK调制的双向光纤无线电(ROF)系统,当传输距离为50 km时,发现OQPSK调制在上行链路中的系统误码率性能优于DPSK调制。文献[15]对比了QPSK调制和OQPSK调制在现代长距离卫星通信系统中的频谱特性,发现OQPSK调制可有效缓解频谱再生长,当数据传输速率到达Gb/s时,系统误码率性能良好。然而,在水下信道条件下,还未有报道OQPSK调制对UWOC系统误码率性能影响的相关文章。
另一方面,由于UWOC系统发送端和接收端的时钟源互相独立,导致最终到达接收端的信号与本地电解调模块的时钟源相位不同步,因此,需要定时误差估计算法来实现位同步。目前,Gardner定时同步算法[16]的应用最广泛,具有同步性能不受载波相位干扰,不需要判决反馈等优点。但在高速率的水下无线光OQPSK系统中采用Gardner定时算法实现位同步时,易产生定时抖动[17],影响系统误码率性能[18]。
本文在高斯光束通过水下信道传播的假设下,研究了OQPSK调制、传输距离和各种水质衰减参数对水下无线光通信系统误码率性能的影响,提出一种基于OQPSK调制的改进Gardner误差估计算法,可以有效地提高同步性能,明显降低误码率。
1 水下信道调制的理论分析
1.1 水下光信道模型
由于光在水下独特的物理特性,在传播时吸收和散射是影响信道损耗的两个主要因素。吸收和散射系数取决于水的类型,文献[3]研究了不同海水类型的衰减系数,如表1所示。
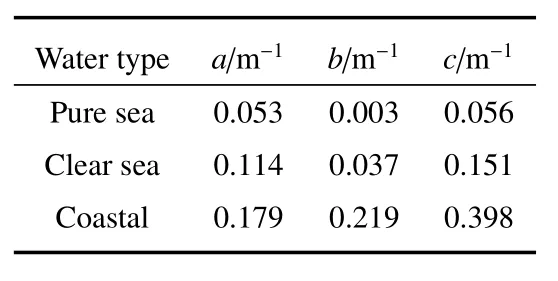
表1 不同水质的典型衰减系数[3]Table 1 Typical attenuation coefficients for different types of water[3]
在UWOC中,水质的总衰减系数可描述为[3]

式中:a(λ)和b(λ)分别是吸收和散射的衰减系数,总衰减系数c(λ)的单位为m-1。
另外,无线光在水下传输时,光束扩展引起的几何衰减对系统性能的影响较大。因此,水下光信道模型可表示为[19]
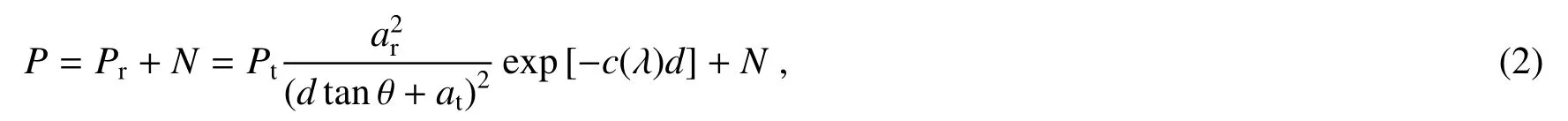
式中:θ为光源发散半角,单位为mrad;at为发射器的孔径半径,单位为mm;ar为光学接收天线的孔径半径,单位为mm;d为光在水下传输的距离,单位为m;Pt是发射信号光功率,单位为mW;Pr是接收信号光功率,单位为mW。背景噪声近似为高斯白噪声N,P为光信号通过水下信道传输后的光功率。
1.2 OQPSK调制解调原理
相比QPSK调制,所采用的OQPSK调制受系统非线性影响小,在带宽受限的水下无线光通信链路,OQPSK信号可以携带更多的频谱,因此频谱利用率和功率利用率高。OQPSK信号的调制解调原理框图如图1所示。
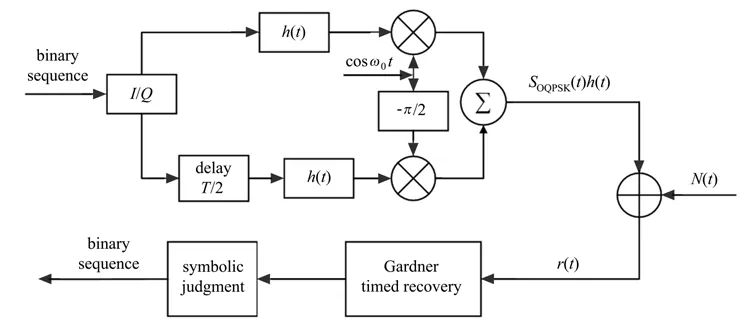
图1 OQPSK信号调制解调模型Fig.1 OQPSK signal modulation and demodulation model
信源产生随机的二进制数据经I/Q变换后,Q支路时延了T/2,分别经平方根升余弦滤波器h(t)和正交载波处理,生成OQPSK基带信号SOQPSK(t)h(t)。再经水下信道传输时,受信道干扰等条件影响,得到信道输出信号为[20]
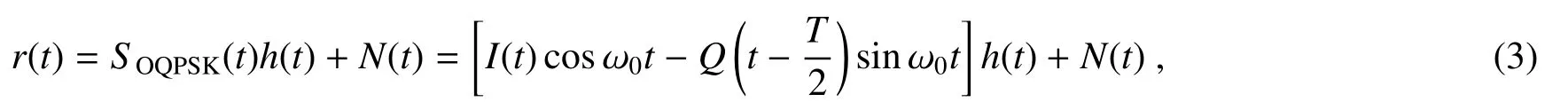
式中:I(t)和Q(t-T/2)分别表示原序列经串并转化后的I路和延时半个周期的Q路,ω0表示载波的角频率,N(t)是背景噪声。
接收端的r(t)经定时同步和符号判决后得到OQPSK的原始二进制序列,下面详细介绍定时同步模块的具体内容。
1.3 OQPSK信号的Gardner定时同步原理
由于Gardner位定时同步算法只要在一个码元中有两个采样点就可以完成同步,所以此处研究水下无线光OQPSK系统中基于Gardner定时算法的同步环路,如图2所示。
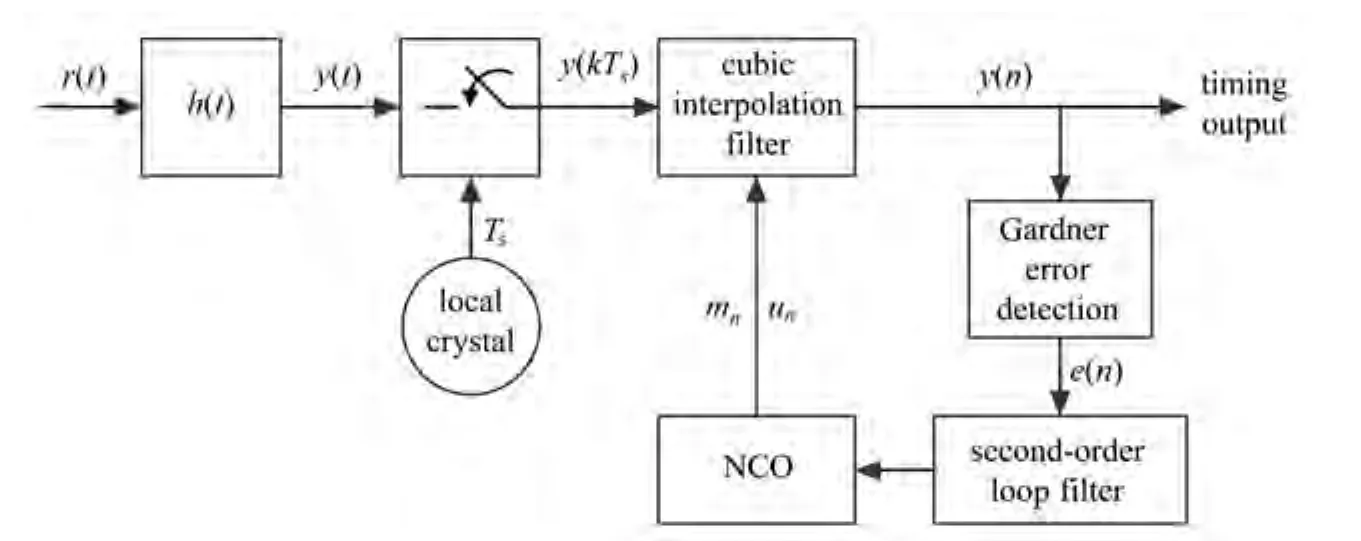
图2 Gardner定时同步环路模型Fig.2 Gardner timing synchronization loop model
由图2所示的Gardner定时同步环路结构,若接收端的OQPSK信号为

式中:T为码元符号的周期,τ为归一化时延。
信号经本地晶振采样后得

式中Sn为采样后的SOQPSK(t)。
经过插值滤波器后第n个码元的插值时刻t(n)可写为
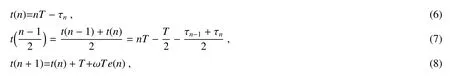
式中:τn是第n个码元的延时估计;ω为定时误差步长参数;e(n)是定时误差,其用来提供最佳采样时刻的调整方向,根据e(n)值的正负来判断定时提前还是滞后,然后通过不断调整最佳采样时刻最终实现符号的准确定时同步。
针对OQPSK信号特点,需将传统Gardner算法中的Q路信号修正为滞后半个码元周期的信号数据,再进行定时误差估算,记为mGA1算法,可表示为
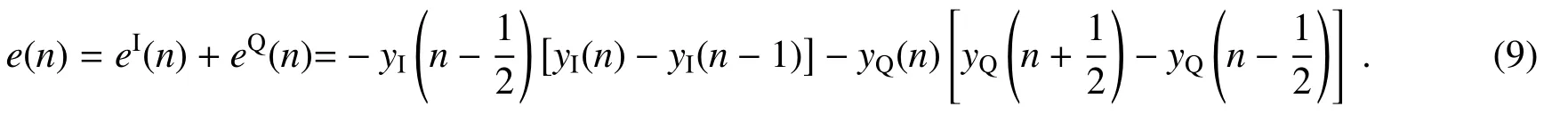
由于mGA1算法存在定时抖动大、计算复杂度高等问题,可采用改进的mGA2算法[21],即当I路或Q路相邻码元符号相同时,分别对eI(n)、eQ(n)取反。但是,通过后续仿真发现,上述两种算法仍然存在同步性差,导致系统误码率较大等缺点,因此提出一种基于OQPSK调制的新的改进算法(mGA3)。
1.4 改进的Gardner时钟误差检测算法
采用IM/DD调制的OQPSK信号在水下信道中发送时,考虑到信道衰减主要影响光信号的强度,使光电转换后的电信号在幅度上具有多值的特点。在这种情况下,即使能准确采样,定时偏差e(n)也不会为零,这不利于同步环路的捕获和追踪。因此,在mGA2算法的基础上,mGA3算法利用最小均方误差(MMSE)准则得到y(n-1/2)与y(n)、y(n-1)的关系,从而进一步改善水下无线光OQPSK系统中的定时误差。其主要思想是:当相邻码元极性不同发生跳变时,需考虑它对中间值的影响,并消除这种影响;当相邻码元极性相同时,考虑如何减小系统自噪声带来的影响。
当相邻符号码元的极性发生跳变时,根据Gardner算法的原理,只需要考虑y(n-1/2)是否存在偏差,进而得到e(n)。由(5)、(7)式可得两相邻采样点和中间点值的关系为

由于h(t)是对称的,根据MMSE准则可得
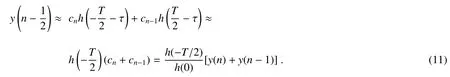
在实际计算时,cn和cn-1不便得到,所以用y(n)和y(n-1)估计。通过上面的分析可知,当定时偏差消除时e(n)为零,则中间采样点的值应始终为零。修正的Gardner定时误差估计可表示为
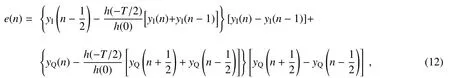
当两相邻码元幅值相同时,理想条件下e(n)为零,但由于系统自噪声的影响,导致环路仍有信号输出。此外,为了降低计算复杂度,将(12)式中的I路和Q路中的乘法后项分别修正为sign(yI(n))-sign(yI(n-1))和sign(yQ(n+1/2))-sign(yQ(n-1/2))来降低乘法运算次数。因此,当相邻码元极性相同时,修正后的部分为零,反之则不为零。由此得到一种基于OQPSK调制的改进Gardner误差估计算法(mGA3)
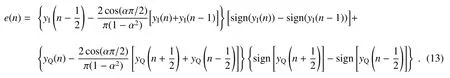
2 基于OQPSK调制的水下无线光通信系统性能分析
2.1 基于OQPSK调制的水下无线光通信系统模型
基于OQPSK调制的UWOC系统模型如图3所示。发送端产生随机二进制序列,对其进行OQPSK调制,添加直流l后,再送给激光器进行光强调制,将产生的光信号利用光学发射天线发射,经过水下信道的传输到达接收端,利用光学天线接收,由光电探测器完成光电转换,再利用Gardner算法实现同步,最后调制得到原信号。
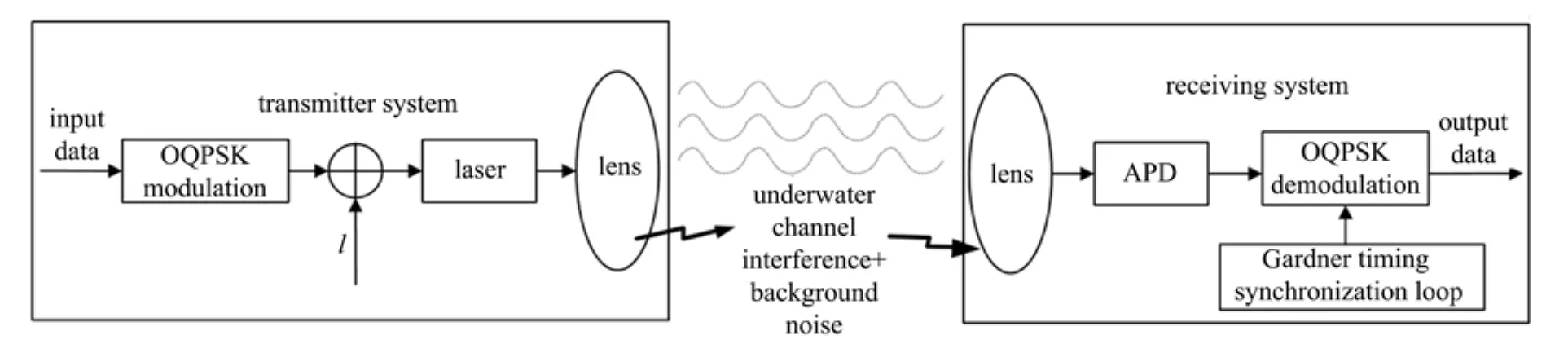
图3 基于OQPSK调制的水下无线光通信系统模型Fig.3 UWOC system model based on OQPSK modulation
结合(3)式可得OQPSK调制水下点对点链路发送端激光器的发射光功率为

式中:δ是电光调制深度,使|δSOQPSK(t)h(t)|≤1;l是为了保证输入激光器的信号为大于工作阈值的正值。
结合(2)、(4)式可得UWOC链路接收端的光功率P(t),可表示为
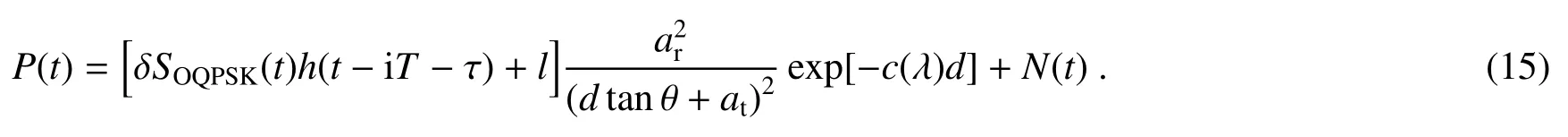
根据本课题组开展的实验和所用器件的实际参数选择系统仿真参数,如表2所示。
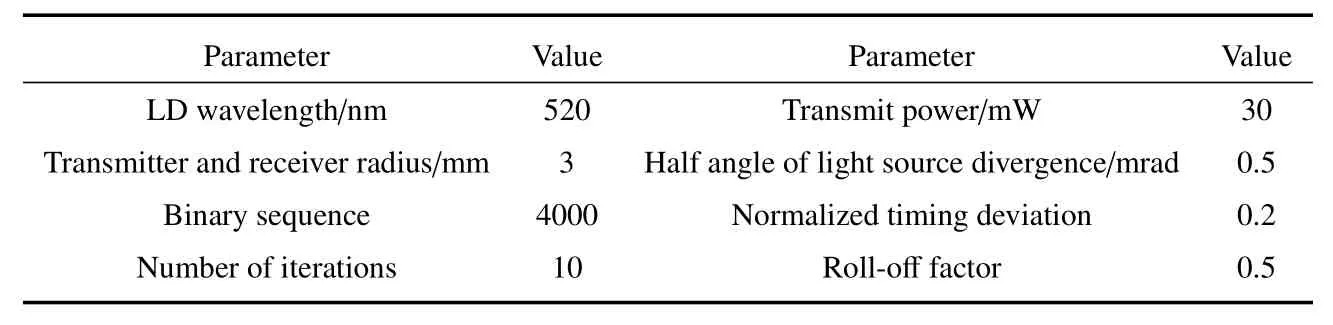
表2 系统参数设置Table 2 System parameter setting
2.2 系统性能仿真分析
为了研究OQPSK调制对UWOC系统误码率性能的影响,通过MATLAB搭建水下无线光通信系统模型,考虑水下光信道传输中光信号的衰减以及时钟的不同步,对比采用OQPSK调制和其他调制方案的系统BER性能。其中,发送端序列为4000,迭代次数为10次,系统其他参数按表2和仿真需要设置,计算BER的方法是对解调后的序列与发端原始序列进行一一对比后统计错误比特数,进而得到系统BER。
首先分析在水质衰减系数c取0.151 m-1(远洋)、传输距离为45 m、系统其它参数按表2设置时,采用OOK、QDPSK、QAM和OQPSK调制的UWOC系统误码率性能,如图4所示。由对比结果可知OQPSK调制方案下的系统性能较好,当系统BER达到10-3时,与使用QAM、QDPSK、OOK调制方案的系统相比分别具有的增益为2.2、4.4、6.2 dB。由此可见,在水下无线光通信系统中OQPSK调制比另外三种调制方案具有明显的优势。
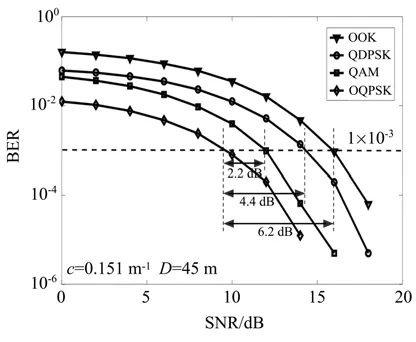
图4 不同调制系统在远洋海水中传输距离为45 m的误码率性能对比Fig.4 BER of different modulation systems with distance of 45 m in the clear sea
接下来分析OQPSK调制在不同水质和不同传输距离下的系统误码率性能,在水质衰减c分别为0.056 m-1(纯海水),0.151 m-1(远洋),0.398 m-1(近海海水),信噪比(SNR)为5 dB时,BER随UWOC链路传输距离的变化情况如图5所示。当系统BER达到10-3时,OQPSK调制比OOK调制的传输距离分别增加8.2、3.3、2.3 m左右。可以看出,在这三种水质下OQPSK调制均优于OOK调制。
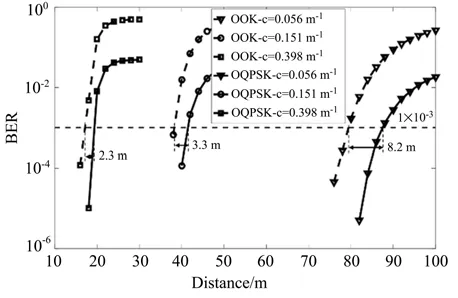
图5 不同水质下OOK和OQPSK的系统误码率性能对比Fig.5 BER of OOK and OQPSK under different water types
当海水信道为远洋水质即c=0.151 m-1时,UWOC系统在不同距离下的BER随水下链路的SNR变化情况如图6所示。当系统误码率为10-3,传输距离为40、45、50 m时,相比于OOK调制,OQPSK调制分别可获得约5.8、6.2、6.3 dB的增益。随着传输距离的增大,OQPSK调制的优势更加明显。
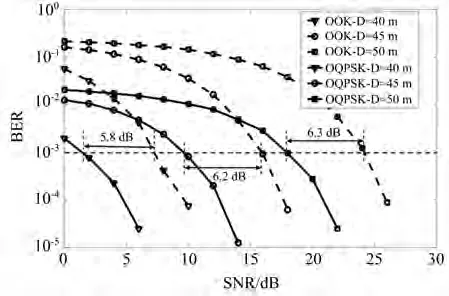
图6 不同传输距离下OOK和OQPSK的系统误码率性能对比Fig.6 BER of OOK and OQPSK under different transmission distance
针对采用Gardner算法的UWOC系统,参数设置如表2所示。经过计算和分析,环路滤波器系数为C1=2-14,C2=2-34。如图7所示,在衰减c为0.151 m-1、传输距离为50 m时,通过对比三种定时同步算法处理后的误码率曲线发现,mGA3算法相比mGA2和mGA1算法,虽然SNR在10~15 dB之间,BER只稍微低一点;但当SNR高于14 dB时,BER明显降低;在SNR为20 dB时,BER降低了近3个数量级。当系统误码率为10-3时,相比mGA2和mGA1算法,mGA3算法可获得12.5 dB左右的增益。
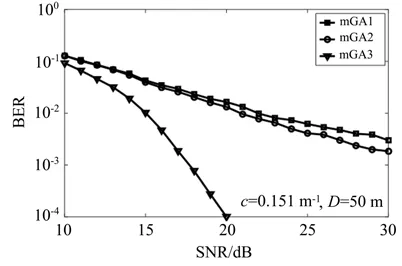
图7 远洋海水中传输距离为50 m的系统误码率性能对比Fig.7 BER of system with distance of 50 m in the clear sea
如图8所示,在衰减c为0.398 m-1、传输距离为22 m,改进的mGA3算法在SNR高于18 dB时,BER达到10-4以下,降低了近3个数量级。当系统BER为10-3时,mGA3算法相比mGA2和mGA1算法,可获得14.2 dB左右的信噪比增益。对比图7发现,不同水质下,采用改进mGA3算法的UWOC系统误码率均能达到10-3以下,性能远优于mGA2和mGA1算法。
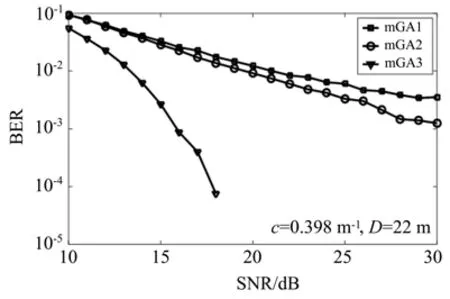
图8 近海海水中传输距离为22 m的系统误码率性能对比Fig.8 BER of system with distance of 22 m in the coastal
3 结论
研究了适用于水下信道的OQPSK调制解调算法,建立了基于OQPSK调制的水下无线光通信系统模型。针对水下信道的衰减特性和系统自噪声,提出了一种改进的Gardner定时同步算法并应用于OQPSK信号的定时同步环路。与mGA2和mGA1算法进行对比,仿真分析了不同水质和传输距离对该系统BER性能的影响。结果表明,采用OQPSK调制的系统与QAM调制系统、QDPSK调制系统和OOK调制系统相比分别可获得2.2、4.4、6.2 dB的增益,有效提升了系统性能;相比于OOK调制,采用OQPSK调制的UWOC系统在不同水质下具有大约2.3~8.2 m的距离增益;在不同传输距离的远洋水质中,OQPSK调制获得了5.8~6.3 dB左右的增益;对比发现,该OQPSK调制系统的BER性能更优。在不同水质下,提出的mGA3算法改善了系统的同步性能,且BER为10-3时,信噪比增益有12.5~14.2 dB左右。本研究仅为软件仿真分析结果,若要正式将OQPSK调制用于实际的水下无线光通信系统中,下一步还需通过硬件实现和实验验证。

