三节点一维相互作用链的非平衡自旋传输特性及其解析公式

郑仰东,高华

(1三菱电机(中国)有限公司研究开发部, 上海 200336;2京都大学低温和物质科学研究中心,日本 京都 606-8501;3华东师范大学,上海 200241)

0 引言

20世纪80年代以来,纳米科技时代的到来使得对介于宏观系统和微观系统之间的介观系统的物理特性及其在纳米材料、器件方面应用的研究变得格外重要。而对介观系统中电子自旋传输特性的理解和探究是纳米电子器件领域的一个主要课题,新兴的自旋电子学则是其主要应用方向。自旋电子学通过开发利用电子自旋态的独特物理特性来实现一些特别的电子学方面的特性和功能,现阶段的研究已显示其卓越的特点,其将在未来的电子学中扮演重要角色[1,2]。应用自旋传输特性的纳米自旋电子器件的一个典型例子是Datta和Das提出的自旋场效应三极管[3-5],其利用Rashba效应(自旋轨道相互作用)来控制通道中二维自旋极化电子气产生的电流;另外如何用自旋态来实现固体量子计算机的量子位(qubit)也是自旋电子学一个有创造性和挑战性的课题[6-15]。

电子自旋传输的特性及其应用主要有以下几个基本问题:自旋极化电子和电流的有效生成和注入,电子媒介中自旋载流子的传输和弛豫,以及对上述物理过程中相关物理量的灵敏检测和物理现象的准确描述等。在纳米尺度的低维系统中,电子自旋传输本质上是一种非平衡过程,因而对这种介观自旋系统非平衡传输过程理论上的理解和研究在电子自旋基础物理和自旋电子学中变得非常重要。目前为止,大部分对介观系统的电子自旋传输的理论研究工作都局限于对平衡过程[16]或单节点及双节点(单量子点及双节量子点)系统非平衡传输过程[17-34]的研究。一般地,多节点(量子点)系统的非平衡电子传输过程的理论方面的研究主要有自旋电流传输过程中的自旋极化、自旋与电子轨道或声子的相互作用现象、磁场和磁性电极对自旋传输的影响、近藤效应、自旋霍尔效应、Aharonov-Bohm效应等几个研究领域,研究方法主要采用非平衡格林函数法(Keldysh理论)、时间依存重整化群法、主方程法、散射贝特假设法等几种基本方法,也有用量子蒙特卡罗法进行大规模数值统计模拟计算的。由于理论分析和推导比较繁琐冗长,特别是同时考虑电子间相互作用时处理更为复杂,对两个以上多节点系统的非平衡传输过程的理论研究中,建立二次量子化的哈密顿算符并运用非平衡格林函数方法的比较少,更没有推导提供数学形式上简练明晰的解析公式的研究报告。本研究中采用Keldysh理论和Hartree-Fock近似对典型的三节点一维(1D)相互作用链模型系统的非平衡自旋传输特性和自旋电荷量分布等进行了较详细的理论分析,并首次推导了一些严密的解析公式,这些公式对从数学构成上理解自旋非平衡传输过程的物理意义有较大帮助,也能应用于由量子点构成的电子自旋系统的分析和设计。同时也提供了部分数值计算结果给予验证,分析计算时系统中每个节点都包含上自旋和下自旋的能级。

本文在1D链模型的哈密顿算符中导入了原位库仑排斥能量项,用以表述上自旋和下自旋电子之间的相互作用。因用于描述热平衡状态下宏观系统的统计力学规律不适合描述介观系统,三节点1D链模型各节点上的初始电荷将显著影响整个系统的非平衡传输特性。从严密推导的三节点1D链模型的基态计算了其各节点上的初始电荷,该基态是基于半填充假设(即1D链上总电子数等于3)推导而得,是一个总自旋为+1/2的反铁磁性基态。从上述初始电荷出发,基于Keldysh理论,推导了在Hartree-Fock近似条件下的三节点1D相互作用链模型的非平衡自旋传输特性(非平衡微分自旋电导和自旋传输电流)和自旋电荷量分布的一些解析公式[35-41]。在Hartree-Fock近似情况下的费曼摄动展开图中,考虑了上自旋和下自旋电子间的两种散射过程:一种是电子被与其相反自旋方向的另一个电子所散射且不改变其自旋方向,这种情况是简单的库仑排斥作用过程;另一种是入射和碰撞电子的自旋方向均变为与原来相反的方向,这种情况源于自旋自由度导致的自旋间相互作用。使用由上述理论构想导出的解析公式,在不同的库仑相互作用能量(U)和绝对零度及有限温度条件下,对仅考虑上自旋和下自旋电子间的库仑排斥力和附加考虑电子自旋与自旋间相互作用的两种情况进行了数值计算。不言而喻,非平衡自旋传输特性和自旋电荷量的分布强烈依赖于上述条件和散射机制。在强相互作用和低温条件下,很容易观测到微分电导的自旋劈裂、电流及节点上电荷的自旋极化等现象。特别是当电极上的偏置电压设定在一定的范围内时,一些节点上电荷的自旋将发生翻转,显示出系统磁特性(铁磁性或反铁磁性)的改变。另一方面,当在散射机制中加入源于自旋自由度导致的自旋间相互作用时,上自旋和下自旋电子间的自旋弛豫作用将削弱自旋传输过程中的自旋劈裂和极化。

本文第1节描述了1D链模型及其哈密顿算符、推导和计算了1D链区域的基态和初始电荷;第2节为理论方法的阐述和解析公式的推导,包括Keldysh理论和Hartree-Fock近似的说明,非平衡格林函数、自旋传输特性和自旋电荷公式的推导等;第3节是数值计算结果和讨论,主要对仅考虑上自旋和下自旋电子间库仑排斥力的情况进行了计算和物理意义的解释,也讨论了因电子自旋自由度引起的自旋与自旋间相互作用的情况;第4节为总结和归纳。

1 模型和初始状态

1.1 模型和哈密顿算符

本研究采用的带三节点1D链模型系统如图1所示,各节点以隧道壁垒相互耦合,每节点包含单一的上自旋和下自旋能级。为研究1D链的非平衡传输特性,1D链区域被连接到能提供流入1D链的非平衡电流的两个外电极。

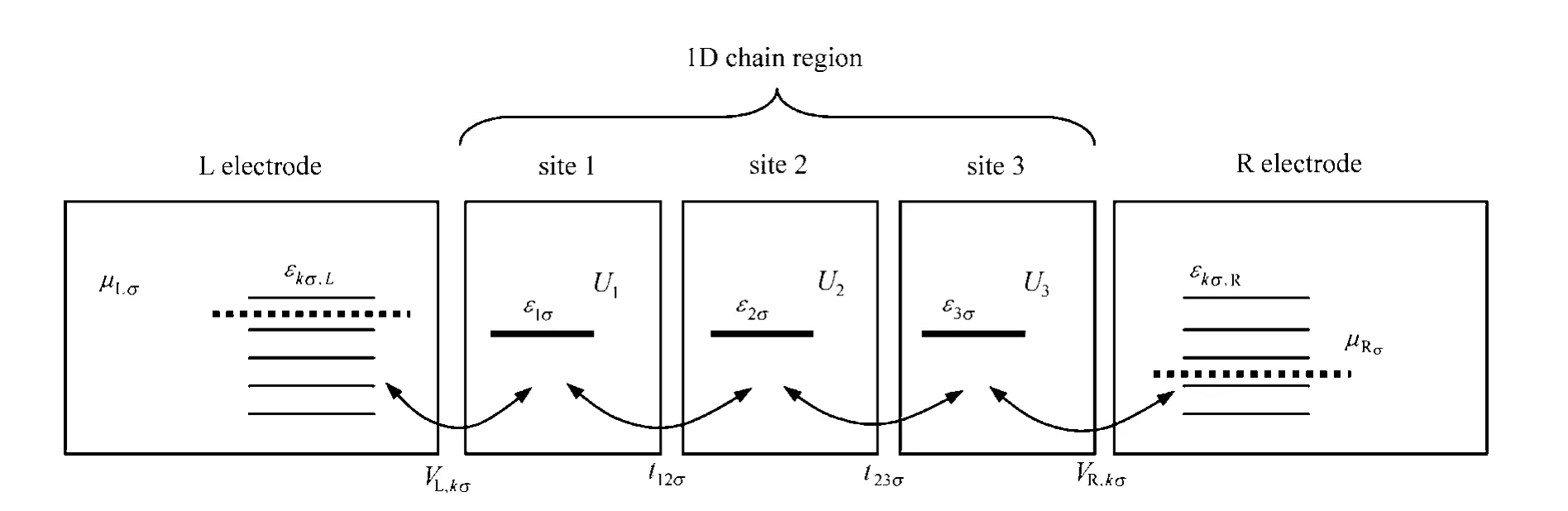
图1 带2个外接电极的三节点1D相互作用链模型系统Fig.1 Model of three site 1D chain system combined with two external electrodes

构造的上述1D链系统的紧束缚哈密顿算符可表示为

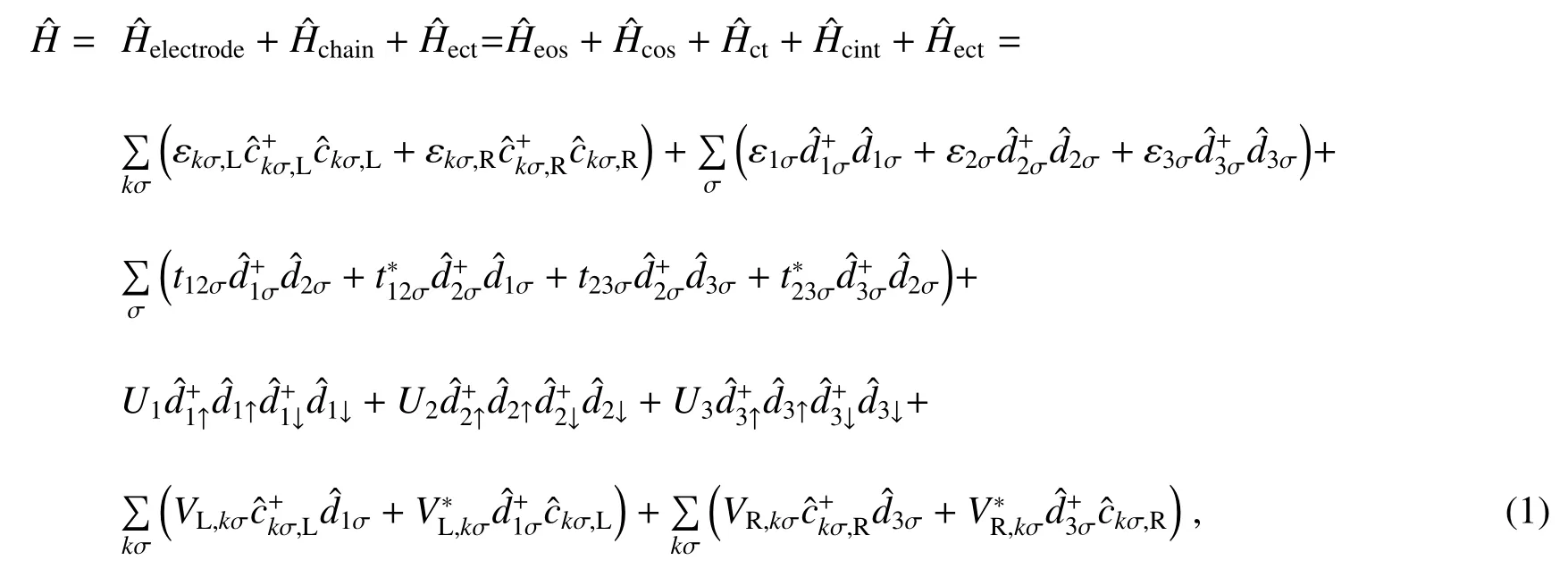
1.2 1D链区域的基态和初始电荷

因电子间库仑相互作用的存在,在t=-∞时还未耦合的1D链模型3个节点的初始状态将影响整个系统的非平衡传输特性。通常初始状态时1D链的总电子数可假定为3个,是半填充状态。在此条件下,通过求解矩阵形式的二次量子化本征方程可以求得1D链体系的全部本征态的严密解,包括基态和激发态。简单起见,假设在(1)式中作为例子,总自旋+1/2的矩阵形式的本征方程表示为

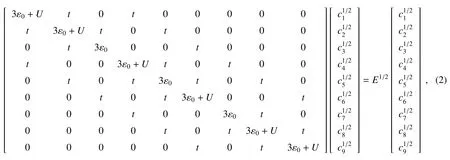
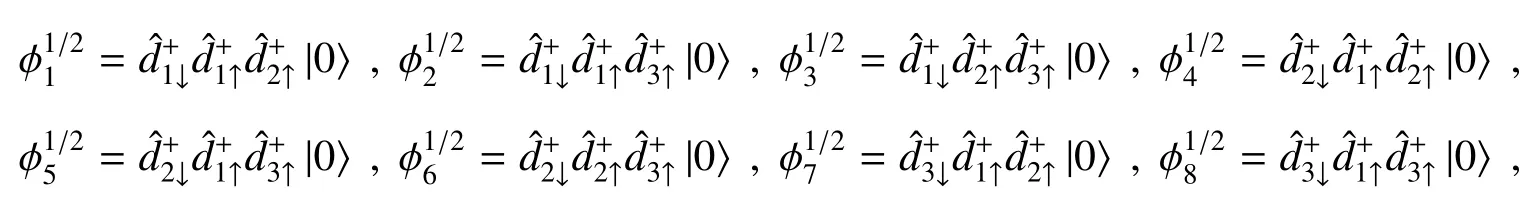
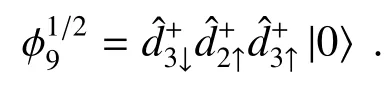
半填充状态的三节点1D链模型共有20个二重或四重简并的本征态,其基态为分别带总自旋+1/2和-1/2的自旋二重态。因用于描述热平衡状态下宏观系统的统计力学规律不适合描述这种介观系统,一般来说,即使在有限温度时系统的状态也应该随机(等概率)地处于上述简并的基态之一(对称性的自发破缺)。不失一般性,选取了从矩阵方程(2)式解出的总自旋为+1/2的一种基态作为1D链的初始态,可表示为

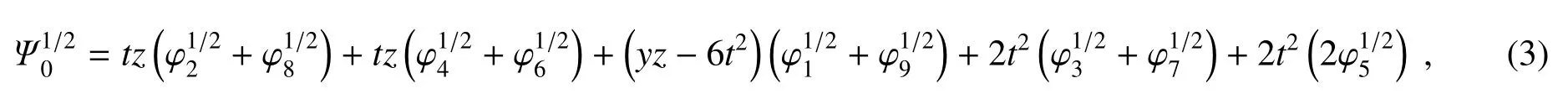
1D链每个节点上的上自旋和下自旋的初始电荷量可以从以上初始态计算获得。表1列出了第3节中数值计算所要用到的在不同库仑排斥能量U条件下的上下自旋的初始电荷量。节点1上的电荷量等于节点3上的电荷量源于1D链模型的对称结构。在节点1和3上上自旋电荷量多于下自旋电荷量,而在节点2上上自旋电荷量则少于下自旋电荷量,提示这是一个反铁磁性系统。上自旋电荷量和下自旋电荷量的差值随着U的增加而增加。

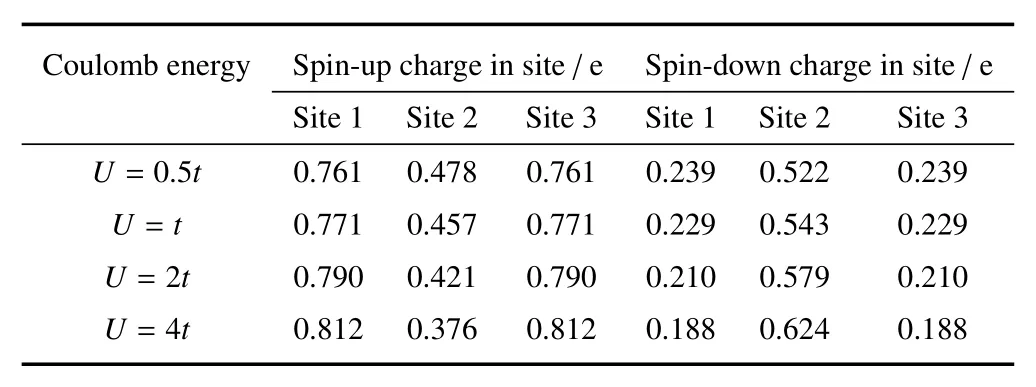
表1 不同库仑排斥能量U条件下三节点1D链模型每个节点上的上自旋和下自旋的初始电荷量Table 1 Initial spin-up and spin-down electron charges in each site of the three site 1D chain model for several different Coulomb repulsion energies U

2 理论方法和解析公式推导

2.1 Keldysh理论和Hartree-Fock近似

为理解Keldysh理论,考虑一个系统包含三个区域:左电极、右电极和中间的1D链,它们在t=-∞时相互不耦合,每个都在无相互作用情况下保持自身的热平衡状态。之后在电极和1D链之间按时间路径t=-∞ → 0→ +∞ → -∞(Keldysh周线)绝热地开启摄动耦合,以此来研究系统的非平衡特性[19-21]。依据量子统计理论(摄动展开)[42,43],在时间t,任何非平衡可观测物理量都可以精确表示为4种类型的Keldysh格林函数(GF),即这里 〈···〉是统计平均的符号(Keldysh理论)[36]。

Keldysh格林函数可以从矩阵形式

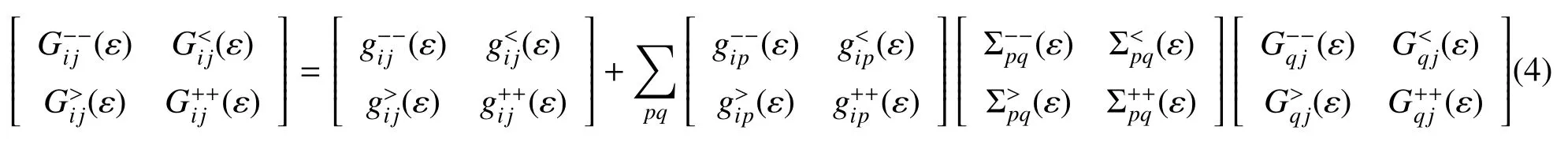
解出,这里在t=-∞的热平衡状态时的非摄动Keldysh格林函数表示为gij(ε),从1D链-电极耦合和库仑相互作用得到的自能量表示为Σij(ε)。通过适当的变换,推迟(超前)格林函数

以及相对应的自能量可分别表示为Gr=G---G＜(Ga=G---G＞)和Σr=Σ--+Σ＜(Σa=Σ--+Σ＞)。这样Dyson方程变换为一种新的形式,可表示为

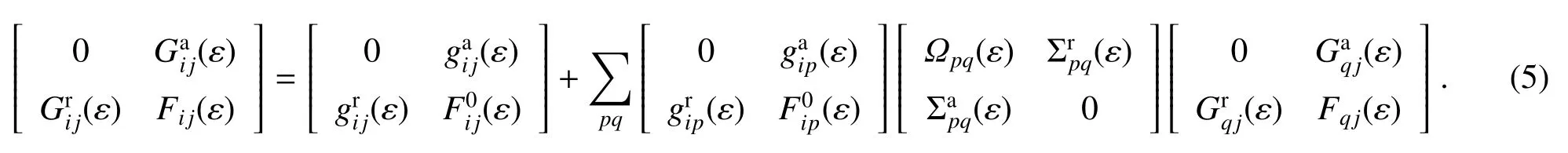
为使推导过程更清楚,定义一个新函数-F格林函数。F格林函数和原来的Keldysh格林函数的关系为F=G--+G++=G＜+G＞,其相对应的自能量是Ω = Σ--+Σ++=-Σ＜-Σ＞。

通过展开(5)式的Dyson矩阵方程,得到了一些直接计算推迟(超前)格林函数和F格林函数的有用公式,分别为

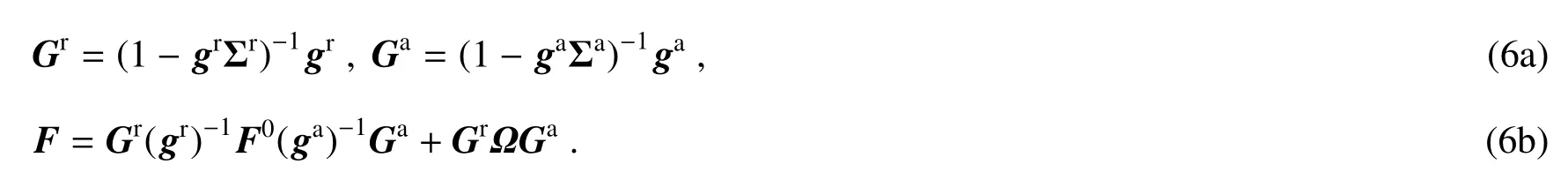
反过来,用推迟(超前)格林函数和F格林函数也可以表达原来的Keldysh格林函数,例如小于符格林函数(lesser GF)可表示为

关于非平衡传输特性,流过1D链的非平衡自旋电流,亦即流过1D链区域和左电极结合部的非平衡电流可表示为

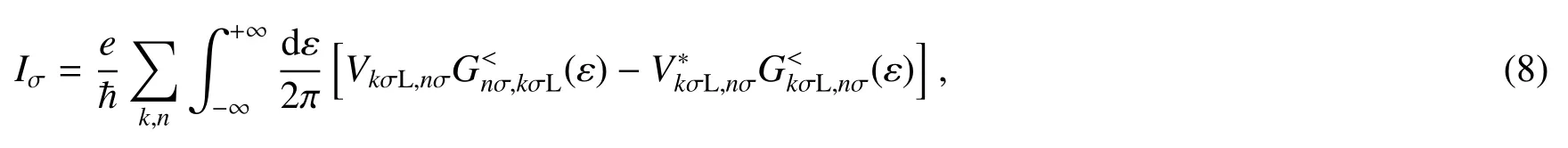
而1D链n节点上的自旋电荷量可表示为[44]

为了推导三节点1D链系统的非平衡格林函数和传输特性的解析公式,首先必须导出Dyson方程中的自能量。

源于1D链区域和左电极耦合部分的自能量可表示为

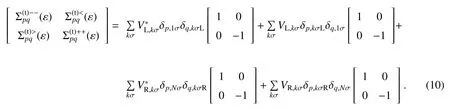
由于这是1D相互作用问题,所以可以简单地推导出来,相对应的推迟(超前)自能量和F自能量可分别表示为

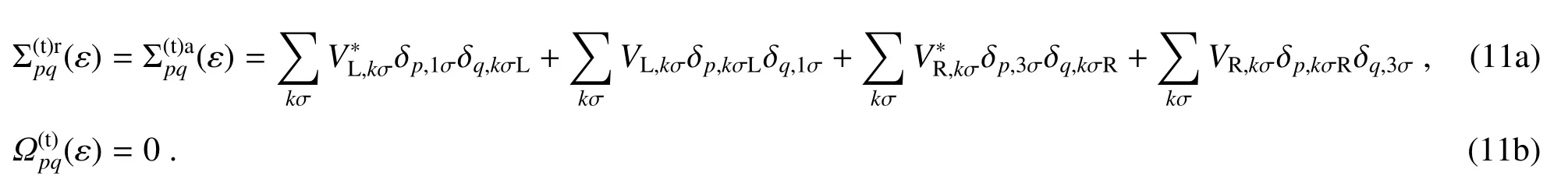
本研究中,对库仑相互作用用包括一部分高阶电子散射过程的Hartree-Fock近似处理,Hartree-Fock近似下的费曼摄动展开图如图2所示,图中考虑了两个上自旋和下自旋间的电子散射过程。一种过程如图2(a)所示,电子被与其相反自旋方向的另一个电子所散射且不改变其自旋方向,这种情况源于简单的上自旋和下自旋间的库仑排斥作用。散射过程中能量的改变表述为库仑排斥能量这种情况下上自旋和下自旋间的自能量分别表示为

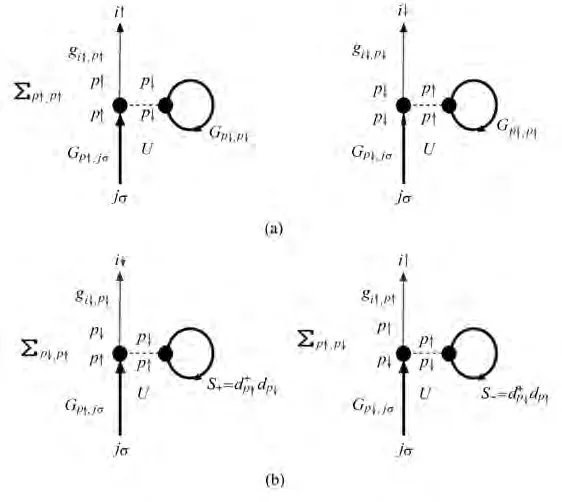
图2 Hartree-Fock近似情况下电子库仑相互作用的费曼摄动展开图。(a)不改变自旋方向的源于上自旋和下自旋电子间库仑排斥能量的散射过程;(b)引起自旋反转的源于自旋自由度导致的自旋间相互作用的散射过程Fig.2 Perturbation expansion diagrams of Hartree-Fock approximation for electron Coulomb interactions.(a)Scattering processes not changing spin orientations due to Coulomb repulsions between spin-up and spin-down electrons;(b)Scattering processes bringing about spin- flips due to spin-spin interactions resulted from spin degrees freedom

相对应的推迟(超前)自能量分别为

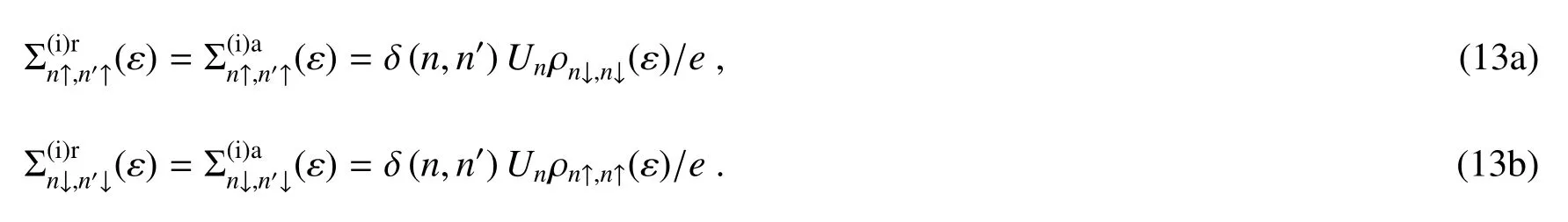
考虑带自旋自由度的传导电子和局域化电子间的散射过程。假设1D链节点上的局域化电子带有自旋和分别代表在x、y和z上的分量值),自旋的产生算符和消灭算符分别由和给出,得到如下有关自旋算符的本征方程:因存在关系式有在1D链n节点上的自旋产生算符和消灭算符的期待值可分别表示为

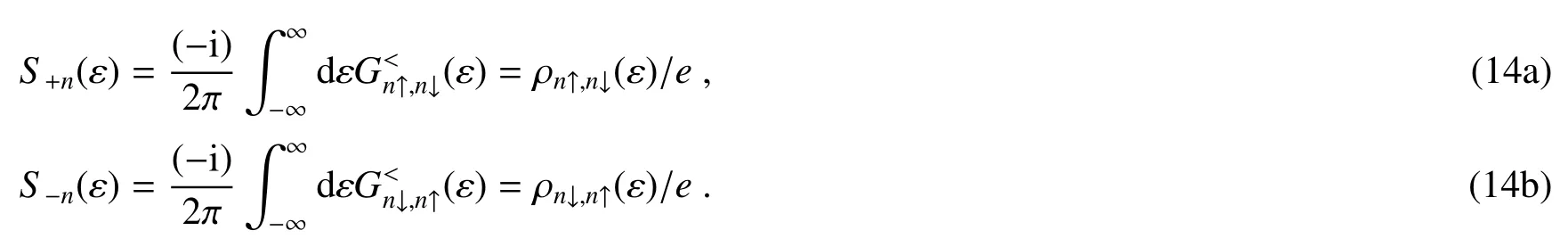
在图2(a)所示的散射过程中,因源于自旋自由度导致的自旋间相互作用,传导(入射)电子和局域化(碰撞)电子的自旋方向同时翻转为相反方向。散射过程中能量的改变表述为自旋翻转能量UnS±n,这种情况下上自旋和下自旋间的自能量分别表示为

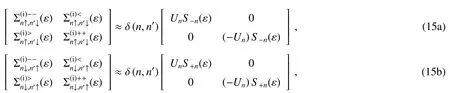
相对应的推迟(超前)自能量分别为

2.2 非平衡格林函数和自旋传输特性

在推导非平衡自旋传输特性之前应先推导出非平衡格林函数。1D链各节点间的推迟(超前)格林函数可从矩阵方程

解出,该方程是从第2.1节(6a)式导出的。这里推迟(超前)格林函数矩阵为包含了代表1D链中每个节点对间格林函数的矩阵元素,i,j=1,2,3。系数矩阵由

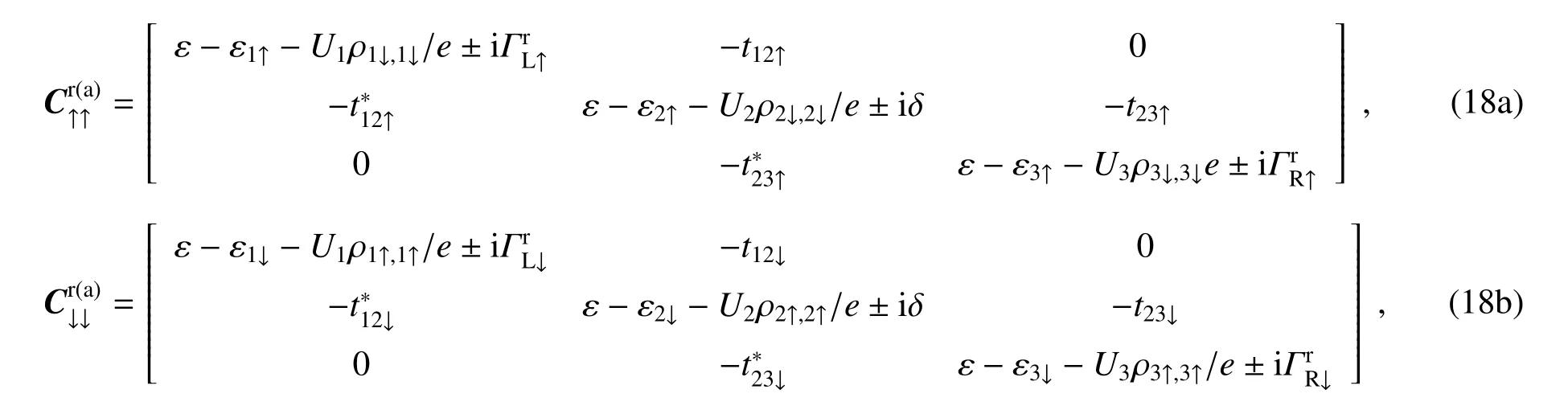
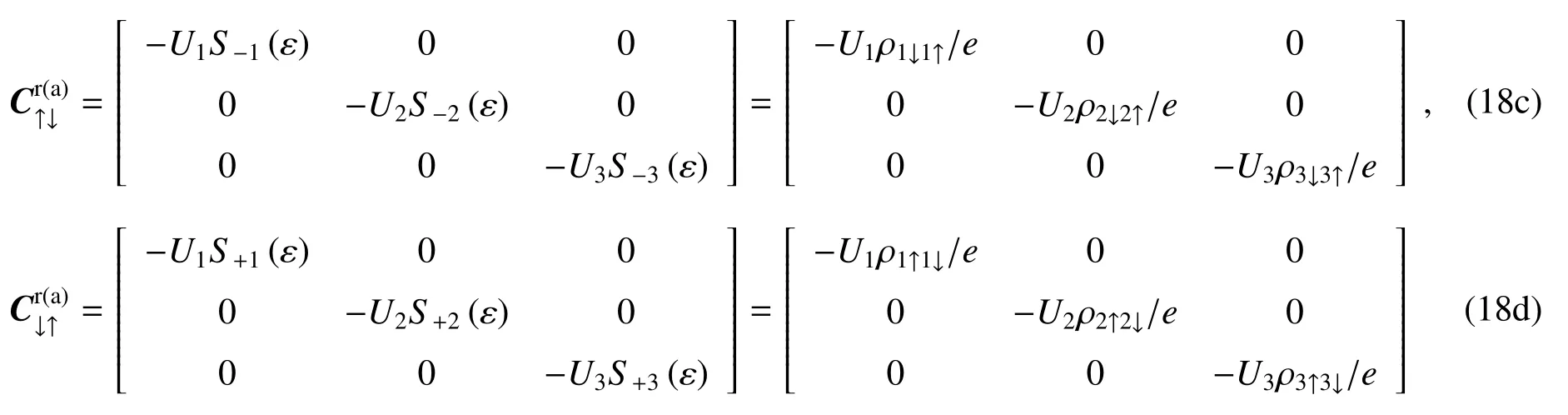
给出,是由第2.1节中自能量的公式推导得到的。这里对应的推迟(超前)自能量其中 να,σ(ε)是电极的电子态状态密度 (DOS),α =L,R。

在仅考虑库仑排斥力的情况下(忽略因局域化电子的自旋方向引起的自旋-自旋相互作用,即从(17)式得到链各节点间相同自旋方向的推迟(超前)格林函数的解析式为

式中

上标和下标(+or-)分别表示推迟和超前格林函数,下标σ和σ¯分别表示具有相反方向的自旋,如↑和↓。

使用推导出的1D链区域的格林函数,得到了1D链上nσ节点电子态(n号节点上自旋为σ的电子态)和左电极及右电极上kσ′电子态(波数为k、自旋为σ的电子态)的推迟(超前)格林函数的解析式为

相似地,左电极及右电极上k1σ和k2σ′电子态的推迟(超前)格林函数的解析式为

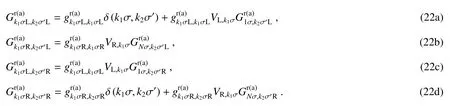
可以按第2.1节的(6b)式,用推迟和超前格林函数导出F格林函数。4种类型的Keldysh格林函数都可以直接从推迟、超前和F格林函数推导得到,仅集中推导和传输特性相关的小于号格林函数(G＜)。

作为推导结果,在1D链上的1σ节点电子态(1号节点上自旋为σ的电子态)和左电极上kσ电子态之间的小于号格林函数的解析式可表示为

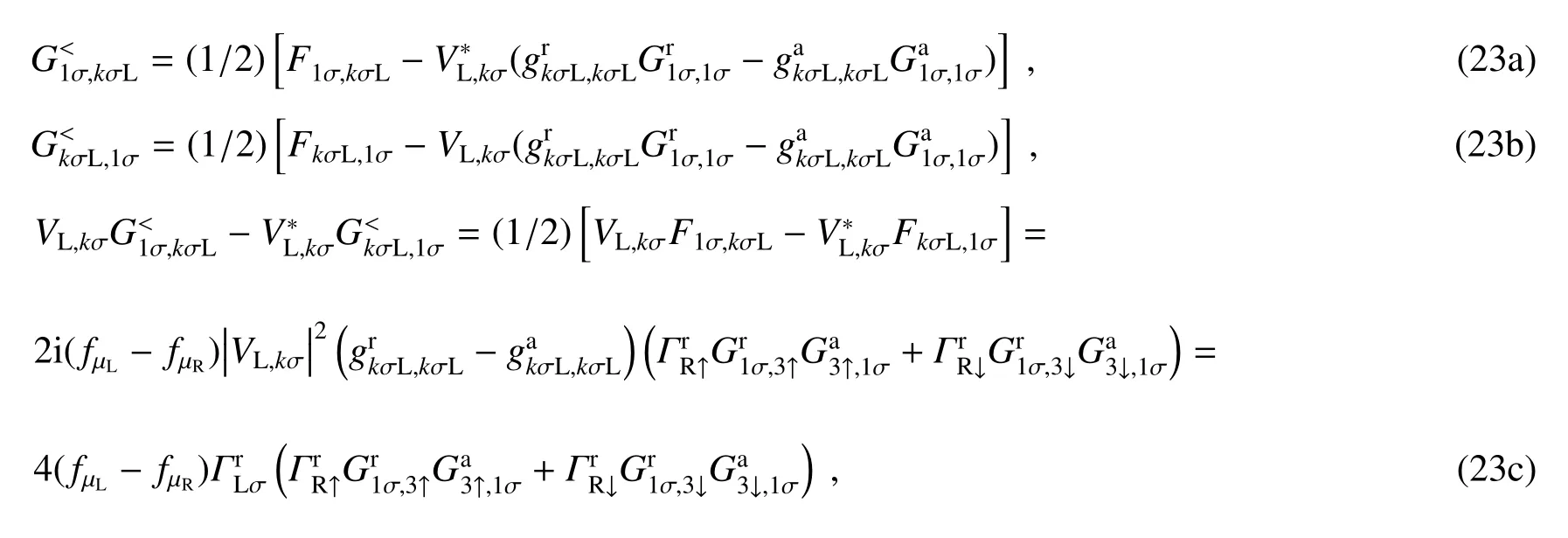
1D链区域的原位小于号格林函数为

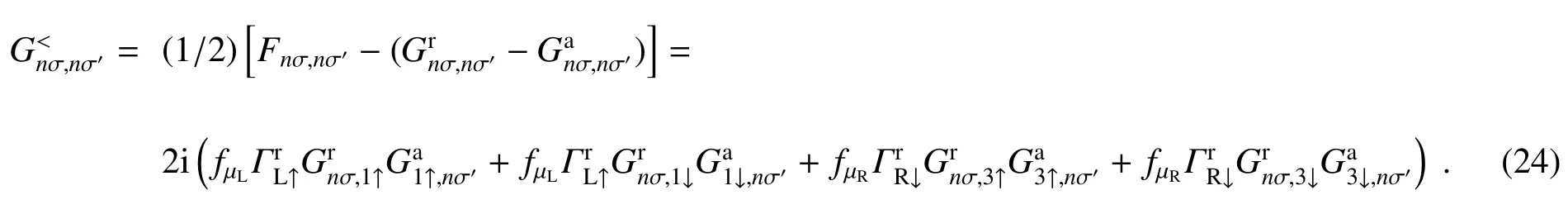
考虑电化学势µL、µR分别加在左电极、右电极时的三节点1D链模型的非平衡传输特性。这等价于在1D链上加上偏置电压V(V=(µL-µR)/e,e为电子电荷量)。以下的非平衡传输特性公式可以从小于号格林函数直接计算推导得到。

流过1D链的非平衡自旋电流与流过1D链区域和左电极结合部的非平衡电流是一样的,把(23c)式代入第2.1节中(8)式,可以推导出

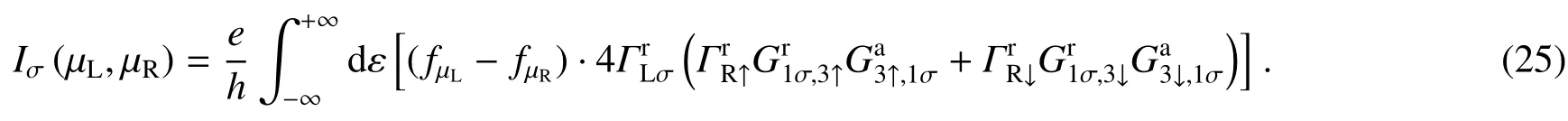
由此可直接得到计算非平衡微分自旋电导(传输系数)的普遍通用的公式为

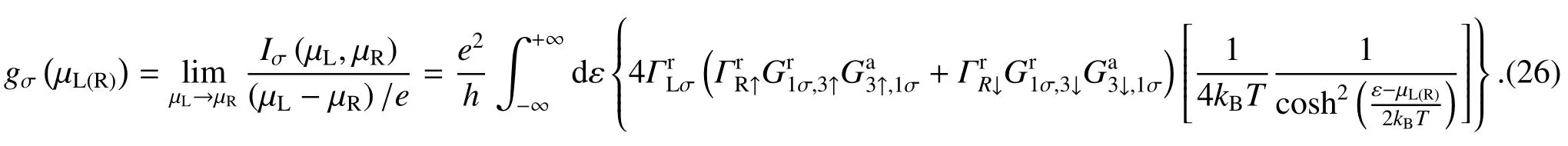
特别是当温度T=0时,(26)式简化为

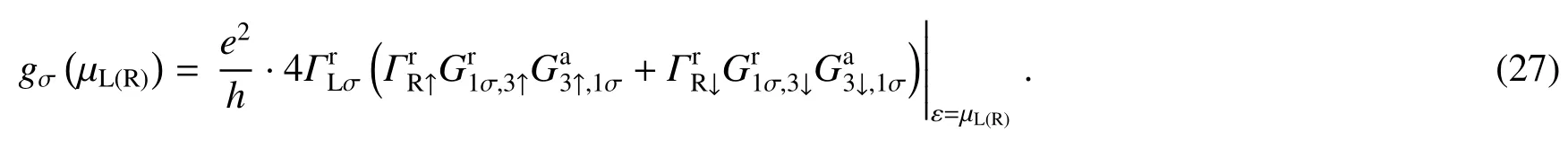
把(24)式代入第2.1节(9)式可以推导出nσ节点电子态对应的非平衡自旋电荷量

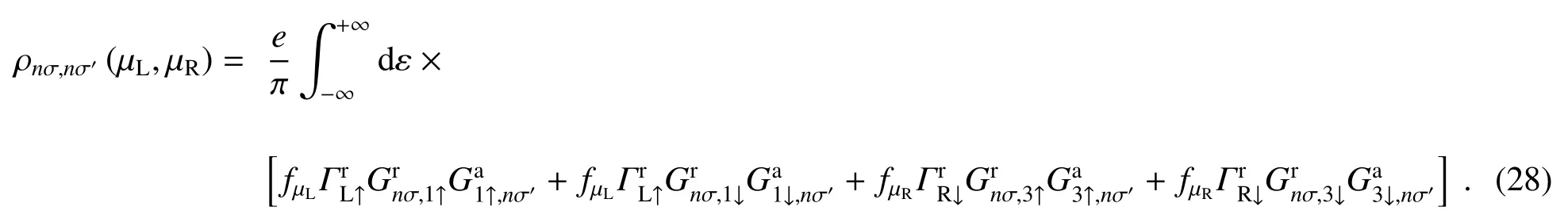
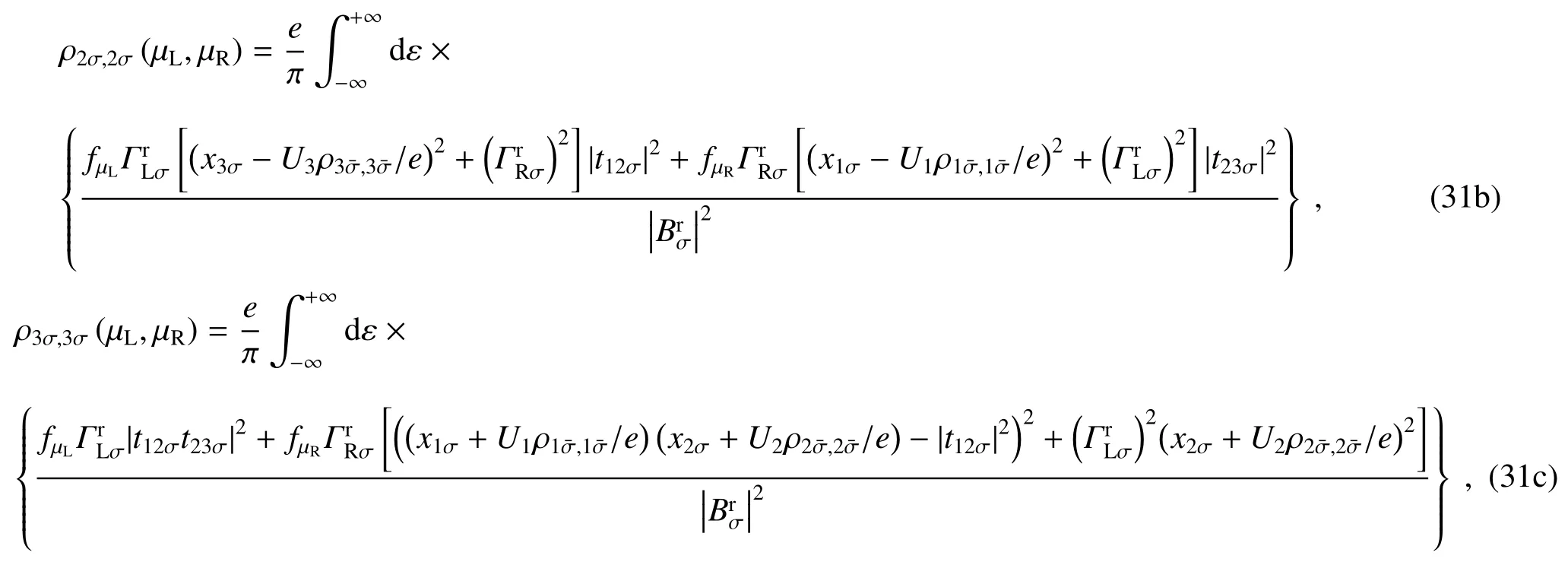
为简便起见,设x1σ= ε- ε1σ,x2σ= ε- ε2σ,x3σ= ε- ε3σ。

考虑以上一维相互作用链的非平衡自旋传输特性解析公式的一些极限情况。在电子间无相互作用(即自旋非极化)的极限条件下,也就是节点上的原位电子库仑排斥能量Ui设定为0时,(29)～(31)式[包括分母变量(20j)]的非平衡微分自旋电导、自旋传输电流和各节点上自旋电荷量的解析公式可以退化到参考文献[45]中的三节点一维非平衡电子传输特性的非平衡微分电导、传输电流和各节点上的总电荷量的解析公式(26)、(24)、(28)[包括分母变量(16j)];把它们与文献[21]中推导的一维紧束缚链模型的非平衡电子传输特性的解析式进行比较,同样也得到了一致的结果。而在节点数从3变为2的极限条件下,上述公式可以退化到以下的2节点一维非平衡自旋传输特性的非平衡微分自旋电导、自旋传输电流和各节点上自旋电荷量的解析公式

利用这些公式得到的数值计算结果和参考文献[17,18]中所报告的一致,上述结果部分验证了所推导解析公式的正确性。

对附加考虑源于自旋自由度的电子自旋与自旋间相互作用的情况,推迟(超前)格林函数的解析公式变得较为复杂,但原理上可从(19)式推导得到。利用上述仅考虑上自旋和下自旋电子间库仑排斥力情况下采用的类似方法,可以直接推导出此情况下的非平衡自旋传输特性(微分自旋电导、自旋传输电流和自旋电荷量等)的基本解析公式,公式由相应各种类型的推迟(超前)格林函数组成。由于篇幅关系,其中的一些主要公式将在其他论文中归纳列出。

3 数值计算结果和讨论

应用前两节计算推导出的节点初始电荷和解析公式,对一些典型参数条件下三节点1D链模型系统的非平衡自旋传输特性进行自洽计算,同时给出其物理解释,从而验证所推导公式的正确性和有效性。

因Hartree-Fock近似方法的限制,选取相对较小的库仑相互作用能量值U(U＜5)来研究库仑相互作用对传输特性的影响。使用针对原位节点自旋电荷量ρnσ,nσ′的自洽计算方法,计算了1D链区域的传输特性。迭代计算的收敛误差在小于0.01%的范围内。1D链每个节点上的初始上自旋和下自旋电荷量(ρnσ,nσ′,σ = σ′)由表 1 给出,而其中所有的初始自旋翻转电荷量项 (ρnσ,nσ′,σ ≠ σ′)设定为 0。

在以下数值计算中,假定 εiσ=0、t12↑↓=t23↑↓=t、VL,k↑↓=VR,k↑↓=V, ΓL↑↓(ε)= ΓR↑↓(ε)= Γ 和U1=U2=U3=U。为简便起见,所有能量都归一化为跃迁能量t,如µL(R)→µL(R)/t、kBT→kBT/t,特别是归一化的自能量定义为γ=Γ/t。为对传输特性进行数值计算,上节公式中的积分计算由辛普森(Simpson)积分公式替代,格点间距设定为典型的dy=10-4。

主要对仅考虑上自旋和下自旋电子间库仑排斥力的情况进行了计算和物理意义的解释,对附加考虑源于自旋自由度的电子自旋与自旋间相互作用的情况也做了一些计算和讨论。

3.1 仅考虑上自旋和下自旋电子间的库仑排斥力

首先介绍仅考虑上自旋和下自旋电子间库仑排斥力时的数值计算结果并给出其物理解释,计算时使用了第2.2节(29)～(31)式。

3.1.1 非平衡微分自旋电导

在零温(kBT=0)和几个不同库仑排斥能量值U的条件下,自能量γ=0.2,1两种情况下的微分自旋电导对电化学势µ=µL=µR的函数依赖关系分别如图3(a1)～(a4)和图3(b1)～(b4)所示。U较小(如U=0.5)时的电导特性和U=0(无相互作用)时的特性非常相似[45]。在这种情况下,当γ=0.2(γ＜1)时,电导曲线在µ=0和有3个尖峰值,提示共振隧穿效应容易发生;而当γ=1(一般γ≥1)时,由于自能量γ的作用,1D链中电子轨道的宽幅变大,这些尖峰将变得不易辨认且将随着γ的增加而逐渐消失。与上述无相互作用时的情况相比较,随着U的增加,微分电导曲线向能量高的一侧平移同时尖峰的宽幅变大。当U＞2γ时,原来的电导尖峰开始分裂成两个尖峰,分别对应上自旋和下自旋电子的电导。该现象可被解释为1D链中带自旋的电子轨道的改变,起因于节点上上自旋和下自旋电子间的库仑排斥作用。库仑排斥作用提升了带自旋的电子轨道的能级能量,也增加了轨道之间的间隔,导致了电导曲线的平移和尖峰的宽变。另一方面,由于在1D链的初始状态中上自旋电荷量大于下自旋电荷量,则在共振点上自旋载流子较少受到下自旋载流子的散射,因而上自旋电流较下自旋电流容易流动,从而上自旋电导的尖峰值先于下自旋电导的尖峰值出现,自旋劈裂现象发生。可以认为微分电导特性曲线上出现的一系列尖峰和低谷是自旋共振隧穿效应和自旋阻塞产生的综合效应。

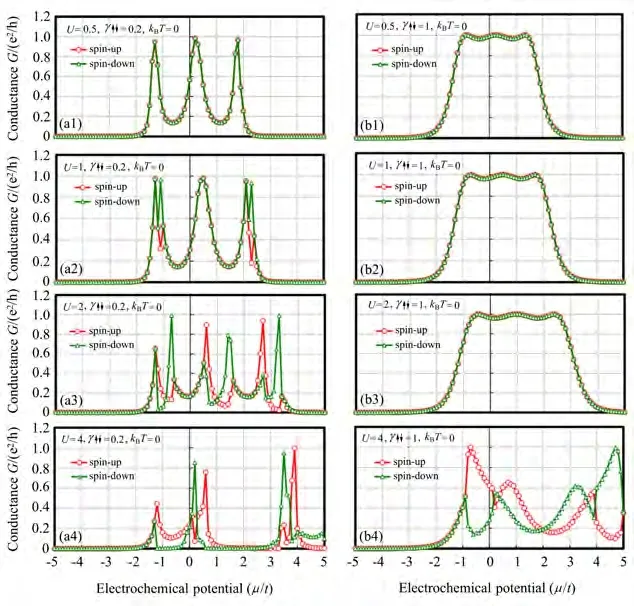
图3 仅考虑上自旋和下自旋电子间的库仑排斥力时,在零温(kBT=0)和不同库仑排斥能量U=0.5,1,2,4条件下的微分自旋电导G(单位:e2/h)对电化学势µ=µL=µR(以跃迁能量t规格化)的函数依赖关系。(a1)～(a4)γ=0.2;(b1)～(b4)γ=1Fig.3 Differential spin conductance G(unit:e2/h)at zero temperature(kBT=0)as a function of electrochemical potentialµ = µL= µR(normalized by transfer energy t)in the conditions of different Coulomb repulsion energies U=0.5,1,2,4,onlyincluding Coulomb repulsions between spin-up and spin-down electrons.(a1)～(a4)γ =0.2;(b1)～(b4)γ =1

当温度对应的热激发能量kBT的大小可以和跃迁能量t和V,或者库仑排斥能量U的大小相比较时,可以容易地观测到自旋传输特性的温度依赖性。以下计算选取了温度kBT=0.1,0.2,0.3来研究1D链的微分自旋电导的温度特性,这时的热激发能量与t、V和U库有相同的数量级。在U=4、自能量γ=0.2和以上这些温度(kBT)条件下的微分自旋电导对电化学势µ的函数依赖关系如图4(a)～(d)所示。与图3(a4)比较,随着温度的升高,与kBT=0相比,自旋电导曲线不再显著地起伏变化而变得平缓,电导的尖峰值也逐渐减小而趋向于电导的平均值。同时上自旋和下自旋电导间的差异也变得不那么明显,在温度较高时自旋劈裂被缓和。以上现象可以理解为:随着温度的升高,传输电子的能级宽度(变动范围)变大,相互重叠混杂区域增加,使传输特性越来越多地包含了各传输电子相互影响后的混合效应,这也是热涨落影响的反映。另外,实际的电子输运系统在温度升高时,由于受外界环境的影响干扰变大,因退相干引起的相干输运变成非相干输运的可能性也会变大。

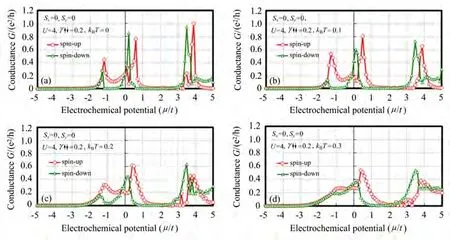
图4 仅考虑上自旋和下自旋电子间的库仑排斥力时,在U=4、γ=0.2和不同温度(kBT)条件下微分自旋电导G(单位:e2/h)对电化学势µ(以跃迁能量t规格化)的函数依赖关系。(a)kBT=0;(b)kBT=0.1;(c)kBT=0.2;(d)kBT=0.3Fig.4 Differential spin conductance G(unit:e2/h)at different temperatures as a function of electrochemical potentialµ(normalized by transfer energy t)in conditions of U=4 and γ=0.2,only including Coulomb repulsions between spin-up and spin-down electrons.(a)kBT=0;(b)kBT=0.1;(c)kBT=0.2;(d)kBT=0.3

3.1.2 非平衡自旋传输电流

图5绘制了在零温(kBT=0)、几个不同库仑排斥能量值U及自能量γ=0.2条件下的非平衡自旋电流对左电极电化学势µL(右电极电化学势固定为µR=-5)的函数依赖关系。当U=0(无相互作用)或0.5(较小值)时,因γ＜1,上自旋和下自旋电流具有相似的特性,增加时呈现间歇式的阶梯形状。该现象提示在这种情况下容易发生自旋电导的量子化[29]。由于库仑排斥作用提升了作为自旋载流子通过1D链通道的带自旋的电子轨道的能级能量,在相同µL的条件下,非平衡自旋电流将随U的增加而逐渐减小。同时上下自旋载流子之间的散射也将导致上自旋电流曲线与下自旋电流曲线分离。当µL靠近一些自旋电导具有尖峰值的位置(共振点,见图3)时,上自旋电流增加而下自旋电流减小,表明1D链中自旋传输电流的极化发生。这个现象也起因于1D链的初始状态,该状态中上自旋电荷量大于下自旋电荷量。在共振点存在带自旋的电子轨道,由于带上自旋的电子轨道能级较低,上自旋电流将先于下自旋电流流动,以至于下自旋电流被抑制,导致下自旋电流减小。当µL到达被带上自旋的电子轨道提升的带下自旋的电子轨道能级后,两个电流趋于相等。在U=4、γ=0.2和几个不同温度(kBT)条件下的自旋电流对µL(µR=-5)的函数依赖关系如图6(a)～(d)所示。与微分自旋电导的情况相似,由于热涨落的影响,随着温度的升高,上自旋电流曲线逐渐地接近下自旋电流曲线,而在温度较高时自旋电流的极化将被缓和。

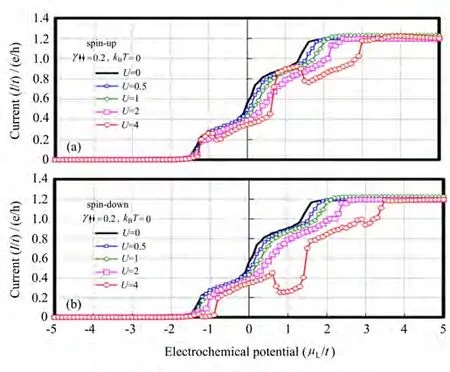
图5 仅考虑上自旋和下自旋电子间的库仑排斥力时,在零温(kBT=0)、不同库仑排斥能量U=0.5,1,2,4及γ=0.2条件下的自旋电流I(以跃迁能量t规格化,单位:e/h)对左电极电化学势µL(右电极电化学势固定为µR=-5,以跃迁能量t规格化)的函数依赖关系。(a)上自旋电流;(b)下自旋电流Fig.5 Spin current I(normalized by transfer energy t,unit:e/h)at zero temperature(kBT=0)as a function of electrochemical potential of the left electrodeµL(electrochemical potential of the right electrode is fixed atµR=-5,normalized by transfer energy t)in conditions of different Coulomb repulsion energies U=0,0.5,1,2,4 when γ =0.2,only including Coulomb repulsions between spin-up and spin-down electrons.(a)Spin-up current;(b)Spin-down current

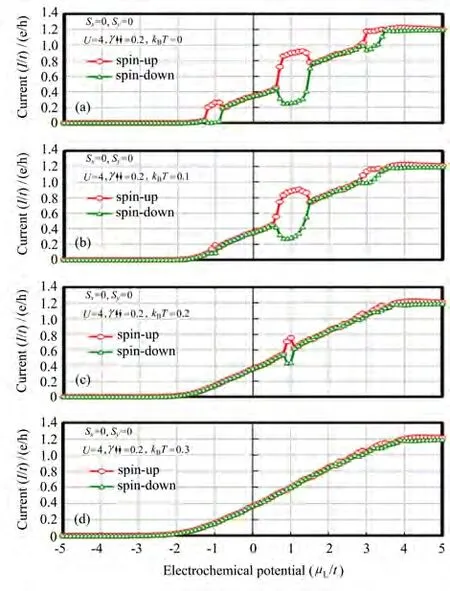
图6 仅考虑上自旋和下自旋电子间的库仑排斥力时,在U=4、γ=0.2和不同温度(kBT=0)条件下的自旋电流I(以跃迁能量t规格化,单位:e/h)对左电极电化学势µL(右电极电化学势固定为µR=-5,以跃迁能量t规格化)的函数依赖关系。(a)kBT=0;(b)kBT=0.1;(c)kBT=0.2;(d)kBT=0.3Fig.6 Spin current I(normalized by transfer energy t,unit:e/h)at different temperatures as a function of electrochemical potential of the left electrodeµL(electrochemical potential of the right electrode is fixed atµR=-5,normalized by transfer energy t)in conditions of U=4 and γ=0.2,only including Coulomb repulsion between spin-up and spin-down electrons.(a)kBT=0;(b)kBT=0.1;(c)kBT=0.2;(d)kBT=0.3

3.1.3 非平衡自旋电荷分布

图7绘制了在零温(kBT=0)、不同U及γ=0.2条件下的1～3节点上自旋电荷量对µL(µR=-5)的函数依赖关系。当U=0(无相互作用)或0.5(较小值)时,1D链中上自旋电荷量的分布与下自旋电荷量的分布相似,且在1D链的边界上形成了电荷壁垒[16]。可以认为自旋电荷量在1D链带自旋的电子轨道(具有有限宽度)中被积累,出于在讨论自旋电流时提到的相同的理由,在相同µL的条件下,自旋电荷量将随U的增加而逐渐减小,同时上下自旋电子之间的散射也将导致上自旋电荷量与下自旋电荷量曲线分离。类似于在讨论自旋电流时的情况,在图3(a4)电导特性曲线的共振点附近,会发生节点上自旋电荷的极化,在相同节点上上自旋电荷量不同于下自旋电荷量。一个有趣的现象是,在低和高的2个共振点附近,在所有节点上上自旋电荷量增加,而下自旋电荷量减小;但在中间共振点附近,节点2上自旋电荷的极化方向意外地与节点1和3上自旋电荷的极化方向相反,即上自旋电荷量减小而下自旋电荷量增加。能用通过详细计算得到的组成1D链带自旋的电子轨道的各节点电子轨道的权重值来解释这个现象。事实上,3个共振点对应于由3个节点电子轨道组成的3个1D链带自旋的电子轨道。粗略计算了组成3个带自旋的电子轨道的3个节点电子轨道的权重值(带自旋的电子轨道的顺序是从低能量到高能量),分别为这里括号中第1～3的值分别表示第1～3节点电子轨道的系数(权重值)。在低能量侧和高能量侧的共振点,其对应的带自旋的电子轨道由第1～3节点的电子轨道组成,在所有3个节点上,上自旋电荷将抑制下自旋电荷;而在中间的共振点,其对应的带自旋的电子轨道仅由第1和3节点的电子轨道组成,在第1和3节点被散射的下自旋电荷将被输运到第2节点,使得第2节点上的下自旋电荷量多于上自旋电荷量。这个发现意味着可能通过µL和µR,或加在1D链上的偏置电压V(eV=µL-µR)来控制1D链是处于铁磁性电子态还是反铁磁性电子态。

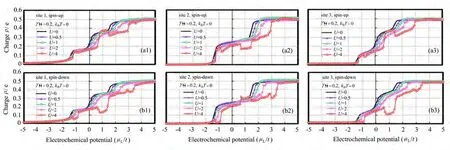
图7 仅考虑上自旋和下自旋电子间的库仑排斥力时,在零温(kBT=0)、U=0.5,1,2,4及γ=0.2条件下的节点上的自旋电荷量ρ(单位:e)对左电极电化学势µL(右电极电化学势固定为µR=-5,以跃迁能量t规格化)的函数依赖关系。(a1)～(a3)1～3节点上的下自旋电荷量;(b1)～(b3)1～3节点上的下自旋电荷量Fig.7 Electronic spin charge ρ(unit:e)at zero temperature(kBT=0)as a function of electrochemical potential of the left electrodeµL(electrochemical potential of the right electrode is fixed atµR=-5,normalized by transfer energy t)in conditions of U=0,0.5,1,2,4 and γ=0.2,only including Coulomb repulsions between spin-up and spin-down electrons.(a1)～(a3)Spin-up charges in sites 1～3;(b1)～(b3)Spin-down charges in sites 1～3

与自旋电流时的情况相似,随着温度的升高,相同节点上的上自旋电荷量曲线逐渐地接近下自旋电荷量曲线,由于热涨落的影响,在温度较高时自旋电荷的极化也将被缓和。

3.2 考虑因电子自旋自由度引起的自旋与自旋间的相互作用

本节介绍附加考虑因电子自旋自由度引起的自旋与自旋间相互作用时的部分数值计算结果并简单叙述其物理意义,计算时使用了2.2节的公式以及附加考虑源于自旋自由度的电子自旋与自旋间相互作用时推导的解析公式(将在其他论文中归纳列出)。

在零温(kBT=0)和几个不同U条件下,对γ=0.2,1两种情况下微分自旋电导对电化学势µ=µL=µR的函数依赖关系分别如图8(a1)～(a4)和图8(b1)～(b4)所示。

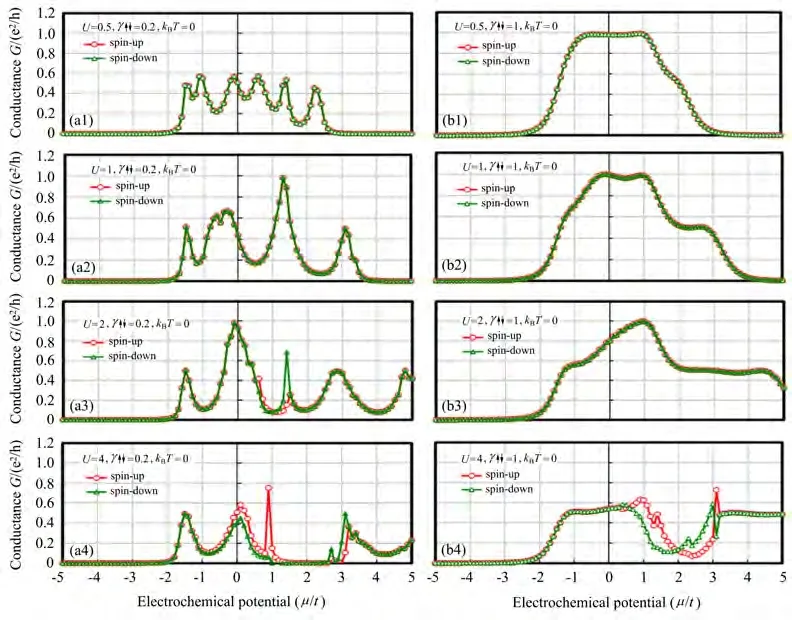
图8 当考虑因电子自旋自由度引起的自旋与自旋间的相互作用时,在零温(kBT=0)和U=0.5,1,2,4条件下微分自旋电导G(单位:e2/h)对µ(以跃迁能量t规格化)的函数依赖关系。(a1)～(a4)γ=0.2;(b1)～(b4)γ=1Fig.8 Differential spin conductance G(unit:e2/h)at zero temperature(kBT=0)as a function ofµ (normalized by transfer energy t)in the conditions of U=0.5,1,2,4,including spin-spin interactions due to spin degrees freedom.(a1)～ (a4)γ =0.2;(b1)～(b4)γ =1

与仅考虑上自旋和下自旋电子间库仑排斥力的情况相比,很明显上自旋和下自旋电导特性的差异变小,表明自旋间相互作用缓和了自旋的劈裂。如第2节所述,这里加入了非零的S±n(ε)[(14a)、(14b)式],将导致非零的系数矩阵从而得到非零的推迟(超前)格林函数以至上自旋和下自旋电子之间的自旋弛豫被增强。另一个较显著的特征是,图7的微分电导特性与仅考虑上自旋和下自旋电子间库仑排斥力时的图3相比较,曲线上出现更多的尖峰值。该现象主要起因于在(25)式的自旋微分电导公式中新添加的非零推迟(超前)格林函数项。举例来说,在仅考虑上自旋和下自旋电子间库仑排斥力的情况下,上自旋电导可表达为而当附加考虑自旋与自旋间相互作用时,该式变为因而可以认为新增加的项使电导特性曲线产生了新的尖峰。

4 总结

采用三节点1D相互作用链模型系统对非平衡自旋传输特性进行理论研究和解析分析。首先从严密推导的半填充假设下的1D链基态计算了其每个节点的初始电荷,该基态是总自旋为+1/2的反铁磁性的电子态。接着基于非平衡格林函数理论(Keldysh理论),阐述说明了研究中使用的基本理论方法并推导了考虑电子间库仑相互作用时在Hartree-Fock近似条件下的1D链模型的非平衡自旋传输特性的主要解析公式(非平衡微分自旋电导、自旋传输电流和自旋电荷分布)。对仅考虑上自旋和下自旋电子间库仑排斥力、以及附加考虑因电子自旋自由度引起的自旋与自旋间相互作用这两种情况都进行了讨论。所使用的解析推导方法是一种普遍适用的严密方法,可推广到对更复杂模型(更多节点和电子能级、任意的链结构等)的非平衡电子传输特性的解析分析和公式推导,在介观和微观量子系统的理论研究中能得到较广的应用。使用以上获得的初始电荷和理论公式,在一些典型参数条件下对三节点1D链模型的非平衡微分自旋电导、自旋传输电流和自旋电荷分布等进行了数值计算,并讨论了计算结果的物理意义,同时也验证了所推导解析公式的正确性和有效性。从计算结果可获如下结论:当仅考虑上自旋和下自旋电子间库仑排斥力时,微分电导特性曲线上出现的一系列尖峰和低谷是自旋共振隧穿效应和自旋阻塞产生的综合效应,随着库仑相互作用能量U的增加,曲线向能量高的一侧平移同时尖峰的宽幅变大,原来的上自旋和下自旋电子的电导尖峰开始分离成两个,发生了自旋劈裂;在电导特性曲线的共振点附近,自旋传输电流和节点上的自旋电荷发生极化,上自旋电流和节点上的上自旋电荷量增加,而下自旋电流和节点上的下自旋电荷量则减小;但在中间的共振点,自旋电荷在节点2上的极化方向与其在节点1和3上的极化方向相反,即上自旋电荷量减小而下自旋电荷量增加,该现象可应用于利用1D链上的偏置电压来控制其磁性电子态(铁磁性态或是反铁磁性态)。当附加考虑电子自旋与自旋间相互作用时,上自旋和下自旋电子的电导特性之间的差别减小,提示自旋间相互作用缓和了自旋的极化。由于热涨落的影响,随着温度的升高,非平衡自旋传输特性曲线变得平滑,在温度较高时自旋劈裂、自旋传输电流和自旋电荷的极化都被缓和。