基于模糊灰色认知图的复杂战场智能态势感知建模方法
陈军, 张岳, 陈晓威, 佟龑
(1.西北工业大学 电子信息学院, 陕西 西安 710072; 2.江苏自动化研究所, 江苏 连云港 222061)
0 引言
现被广泛认可的态势感知(SA)概念是由Endsley于1995年提出,并经过一系列讨论后形成的定义——“对特定时空中态势元素的觉察、理解以及对其未来状态的预测”。战场SA相当于“观察- 判断- 决策- 行动(OODA)”环路中的观察和判断环节,是指挥员认知决策和无人系统智能决策的基础,是一种在复杂对抗环境中启发决策活动的认知理论,如图1所示。

图1 SA与决策的关系Fig.1 Relationship between SA and decision making
由于SA概念起源于对人的认知活动的研究,目前国内外SA的研究主要集中于人在任务过程中的SA理论模型、度量模型和应用模型等问题。但随着未来无人系统在战场中的广泛运用,开展复杂战场环境下的智能SA问题研究势在必行,它将提高无人系统的智能SA水平。
近些年来,将认知工程科学、人工智能技术应用于无人系统的研究成为重要趋势。其中,模糊认知图(FCM)作为一种较理想的、可用于建模和模拟动态系统知识表示和决策支持的工具,其节点具有明确含义、结构具有反馈机制、容易引入学习机制等优势使其应用范围非常广泛,目前已有众多研究者将其应用于战场SA的建模工作,以期为指挥人员或无人系统的作战任务提供决策支持。因此,本文基于SA理论的3层次概念框架,针对现代战场环境的动态、不确定性特点,采用FCM的扩展形式——模糊灰色认知图(FGCM),建立战场环境下目标SA模型,提升无人系统的决策优势。
1 战场智能SA建模分析
1.1 战场SA建模分析
按照SA理论的3层次概念框架,战场SA同样包含了态势元素的觉察、态势的理解和态势的预测3个阶段。态势觉察主要解决战场态势数据信息的预处理,态势理解和态势预测主要通过态势数据信息的关联和推理,获得对当前战场态势的综合评价和趋势判断。
目标威胁评估和意图预测分别是战场态势理解和态势预测中最重要的内容之一。在威胁评估领域,目前常用的方法有贝叶斯网络、多属性决策、神经网络等。其中,贝叶斯网络和神经网络都属于量化类威胁评估方法。不同的是贝叶斯网络方法的评估结果往往以离散化的威胁等级及其概率形式呈现;神经网络方法在有数据支撑的情况下,可以量化输出连续的威胁值。多属性决策方法属于威胁排序类评估方法,以经典的逼近理想解(TOPSIS)法为例,它是通过比较有限个评价对象与理想化目标的接近程度来评价各方案的相对优劣,计算的综合评价指标只作为排序的依据,不能量化威胁值,进而无法对单一目标进行威胁评估。在意图预测领域,目前常用的方法有贝叶斯网络、神经网络、模糊推理等。其中,贝叶斯网络和模糊推理方法需要依赖专家先验知识构建初始模型,在有数据样本的条件下可对模型进行优化;神经网络方法主要采用数据驱动的建模与推理方式,在用于意图预测时可以将目标的态势数据和真实意图标签作为学习的样本,可以在无需先验知识的情况下达到较高的预测准确率。
由此可见,在复杂、动态、不确定战场环境的SA建模问题中,对于贝叶斯网络建模方法,在分布独立这个假设成立的情况下,即使数据存在缺失、不完备等情况,贝叶斯网络也能取得很好的建模效果。但考虑实际战场中各态势要素之间可能具有不同程度的关联,不能满足分布独立的假设前提,如何改进和弱化独立性假设对贝叶斯网络建模的影响,还需要继续探索。神经网络建模方法在大量训练数据支撑下可以达到很高的拟合精度且不依赖于先验知识,但实际战场中的数据通常难以获得;同时由于干扰等因素,数据存在不确定、不完整的特性;另外,神经网络隐含层节点无语义,推理过程具有“黑箱特性”,对神经网络建模方法的实际应用产生了一定的限制。多属性决策和模糊推理法建模过程简单,推理速度快,但模型相对固定,在具有反馈的动态复杂系统建模上有一定困难。
因此,本文主要考虑到战场环境的动态性和数据的不确定性,尝试利用FGCM在表达和处理不确定数据、可解释的因果推理机制等方面的建模特点,加入环境控制节点,改善威胁评估模型的动态适应性;同时引入学习算法减少建模中对专家先验知识的依赖,优化模型参数,以期提高意图预测的客观性和准确性。战场智能SA建模过程如图2所示。

图2 战场智能SA建模过程Fig.2 Modeling process of intelligent situation awareness in the battlefield
表1所示为战场目标SA建模内容分解与技术途径。在态势觉察阶段,利用FGCM模型的灰数表达方式实现不同来源、不同结构态势元素的不确定性描述和量化;在态势理解阶段,以目标威胁评估为研究对象,通过引入外部环境变量,建立能够适应战场环境动态变化的威胁评估动态模糊灰度认知图(DFGCM)模型;在态势预测阶段,以目标意图预测为研究对象,通过引入粒子群优化(PSO)算法提高模型对历史数据的参数学习能力,减少模型对专家知识的依赖,实现知识与数据的双驱动。

表1 战场智能SA建模的技术方法Tab.1 Technology and method of battlefield intelligentsituation awareness modeling
1.2 FGCM建模方法


图3 经典FCM与FGCM关系示意图Fig.3 Schematic diagram of relationship between FCM and FGCM
灰数的不确定程度计算公式如(1)式所示:
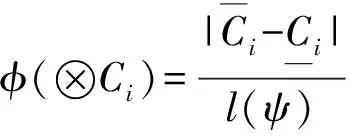
(1)


(2)
FGCM的节点状态值推理公式如(3)式所示:

(3)
式中:表示节点前一时刻状态值对当前状态值的影响,取值范围为[0,1]。
激活函数(·)主要有sigmoid型和tanh型,分别对应节点状态值属于[0,1]和[-1,1]两种情况。

(4)

(5)
式中:为激活函数调节系数;灰数的加法、乘法运算法则如下:

(6)

(7)
将灰数转化为准确值的操作过程称为白化,白化的一般公式为

(8)
式中:为调节白化值偏向的参数,取值范围为[0,1]。
在FGCM的实际应用中,概念节点数据的量纲各不相同,需要通过模糊化操作转变为无量纲的模糊数。将FGCM应用于动态不确定战场环境的SA建模问题具有以下4点优势:
1)FGCM采用灰数形式进行推理,加强了表达和处理不确定数据的能力,并可实现不确定推理结果的量化输出;
2)通过引入环境控制节点,构建基于DFGCM的威胁评估模型,与TOPSIS法相比,不仅能够量化目标的威胁程度,还能在模型推理过程中响应外部环境的动态变化;
3)FGCM模型为有向有环图,可以对贝叶斯网络、模糊推理等方法难以表示的节点间存在关联或具有反馈的复杂系统进行建模;
4)与神经网络相比,可利用FGCM模型节点的语义性,基于专家先验知识构建可解释的意图预测模型结构,再引入学习算法,进而在可用数据支持下确定模型参数。
2 基于DFGCM的威胁评估建模
任务想定设定为对入侵飞机目标的战场目标SA建模,主要包含态势觉察、威胁评估和意图预测3个模块。态势觉察既受自下而上的数据信息驱动,也受到自上而下的任务驱动。
建模过程中,采用受任务驱动的态势觉察方式,以意图预测为最终目标,自上而下进行态势元素的分解,指导态势觉察模块从战场环境中提取相关的态势元素,并经过不确定性表达与处理后,提供给威胁评估和意图预测模块。受任务驱动的自上而下态势元素分解过程如图4所示。

图4 受任务驱动的自上而下态势元素分解Fig.4 Task driven top-down decomposition of situation elements
由于与目标识别等问题不同,威胁评估具有一定的主观性,主要是作为后续行动的依据,评估结果的有效性很难直接体现。在模型权值的确定中直接引入学习机制比较困难,故需要一定的专家经验和知识,一般是利用多个专家知识进行加权确定初始权值。因此,本文对于威胁评估的建模主要考虑动态性特征,需要提取的态势元素主要包括两大类:1)与目标能力和时空关系有关的元素,如目标机动能力、隐身能力等,作为模型的概念节点;2)反映动态战场环境的元素,如地形、气象、敌方支援、电子干扰等自然因素和人为因素,作为模型的外部控制节点。
基于态势元素分解确定的概念节点及其因果关系,构建基于FGCM的目标威胁评估模型;分析外部控制节点对概念节点之间因果关系的影响情况,确定与FGCM关联权值⊗,的动态函数,使模型推理适应动态变化的战场环境。图5所示为基于DFGCM的目标威胁模型,图5中威胁评估DFGCM模型的节点定义如表2所示。

图5 基于DFGCM的威胁评估模型Fig.5 Threat assessment model based on DFGCM
威胁评估模型在推理过程中,权值可根据外部控制节点的状态动态调整,如(9)式~(12)式所示,权值的调整受其初始值和环境影响关系的共同作用。
当⊗,为正值,因果关系受影响增强时:
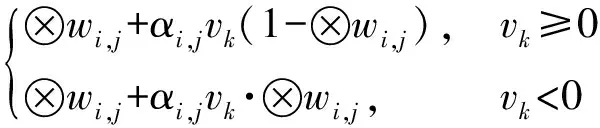
(9)
当⊗,为正值,因果关系受影响减弱时:
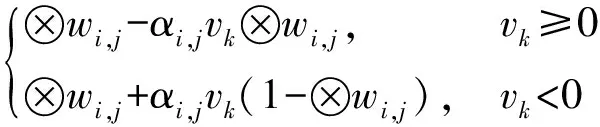
(10)

表2 威胁评估DFGCM模型的节点含义Tab.2 Node meaning of threat assessment DFGCM model
当⊗,为负值,因果关系受影响增强时:

(11)
当⊗,为负值,因果关系受影响减弱时:

(12)
式中:表示第个外部控制节点的状态值;,为调节系数,取值范围为[-1,1],它决定了动态调节的力度和方向。当多个控制节点同时对一个权值⊗,起作用时,只选取使该权值变化最大的。
DFGCM模型的输出为灰数,即区间数的表达方式。为了进行有效的排序,需要进行白化。考虑到模型输出具有的不确定性越大,表示我方对目标掌握的信息和情报越少,敌方对我方的威胁越接近推理结果的上限。因此白化公式(8)式中参数的确定按照(13)式进行:

(13)
式中:(⊗)表示节点⊗根据(1)式计算出的灰度。
3 基于FGCM的意图预测建模与学习算法
目标意图预测模型的概念节点来自态势觉察模块分解的态势元素,同时包含了威胁评估模块输出的目标威胁程度信息。表3所示为意图预测FGCM模型的节点定义。
分析各概念节点之间的因果关系,可以构建意图预测FGCM模型,如图6所示。入侵目标飞机的作战意图节点(⊗)包括攻击、侦察、掩护和其他4种类型,通过对输出节点⊗状态值的白化后,根据阈值判断具体意图类型,其中、、为4种意图的分类阈值。

表3 意图预测FGCM模型的节点定义Tab.3 Node definition of intention prediction FGCM model

图6 基于FGCM的意图预测模型Fig.6 Intention prediction model based on FGCM
由于实际战场SA中的目标意图类型有限,意图预测问题可以归结为分类问题,与威胁评估不同的是目标意图是客观的,不同战术意图下所表现出的态势元素特征也不同。在有数据支撑的条件下,可将目标真实意图作为标签,引入学习算法确定权重,可以避免过度依赖专家知识,并提高目标意图预测的客观性、准确性,也符合智能战场SA的发展趋势。
本文引入种群学习算法中常用的PSO算法,学习和调整意图预测FGCM模型的关联权值。PSO算法中的个体由图6模型中的非零权值组成,其中非零权值有9个,每个灰数权值由上、下限值组成,因此个体编码长度为18位,如图7所示。由FGCM的定义,在种群初始化和迭代过程中,上限值要大于或等于下限值,且在[-1,1]范围内。

图7 个体编码及其初始化Fig.7 Individual coding and its initialization
经过编码后,种群中每个个体就是一组权重值,评价一组权重值的优劣,需要设计适应度函数。适应度函数设置为训练数据的分类准确率,
=
(14)
式中:为相应权值在训练数据下推理正确的个数;为训练数据的总组数。因此,本文PSO算法中每一个个体,就是意图预测FGCM模型中的一组权重,适应度函数就是用来评价个体优劣(即接近理想权重的程度)的标准,对于每一个个体,将其代表的权重代入模型,然后根据一组训练数据中的输入节点⊗~⊗推理出输出节点⊗的值并进行白化,根据白化值和图6中的阈值~判断是否分类正确,根据(14)式计算出每一个个体代表的权重在26组训练数据下的分类准确率,作为其个体适应度。个体适应度越大,表明该个体代表的权重推理出的分类准确率越高,该个体越优,后续种群的更新就要不断向个体适应度更高的个体靠近,取寻找最理想的权重矩阵。同时,由于推理结果⊗是一个灰数,分类结果由此灰数值白化后得到,推理结果的灰数不应包含太大的不确定度。因此,判断个体的优劣时还要考虑输出节点的不确定性,选择推理结果不确定性更小的个体作为更优个体。故将训练数据下输出节点⊗的平均不确定度作为判断个体优劣的第2个指标:

(15)
式中:(⊗)为由第组训练数据推理出的节点⊗的不确定度,其计算方法在12节已经给出。
综上所述可知,评价个体优劣时,先计算其适应度函数,适应度函数更大的个体更接近最优解;当两个个体适应度函数相同时,再计算节点⊗的平均不确定度,取平均不确定度更小的个体为更优个体。随着迭代的进行,准确率高、平均不确定度小的个体得以保留,最终找到一个和都令人满意的全局最优解作为权重矩阵的学习结果。
PSO算法中,种群的更新根据以下2个公式进行:

(16)

(17)

对种群中每个粒子都用(16)式、(17)式进行更新,随着迭代步数的增加,整个种群不断地向全局最优解靠近,最终找到令人满意的解。PSO算法的流程如图8所示。
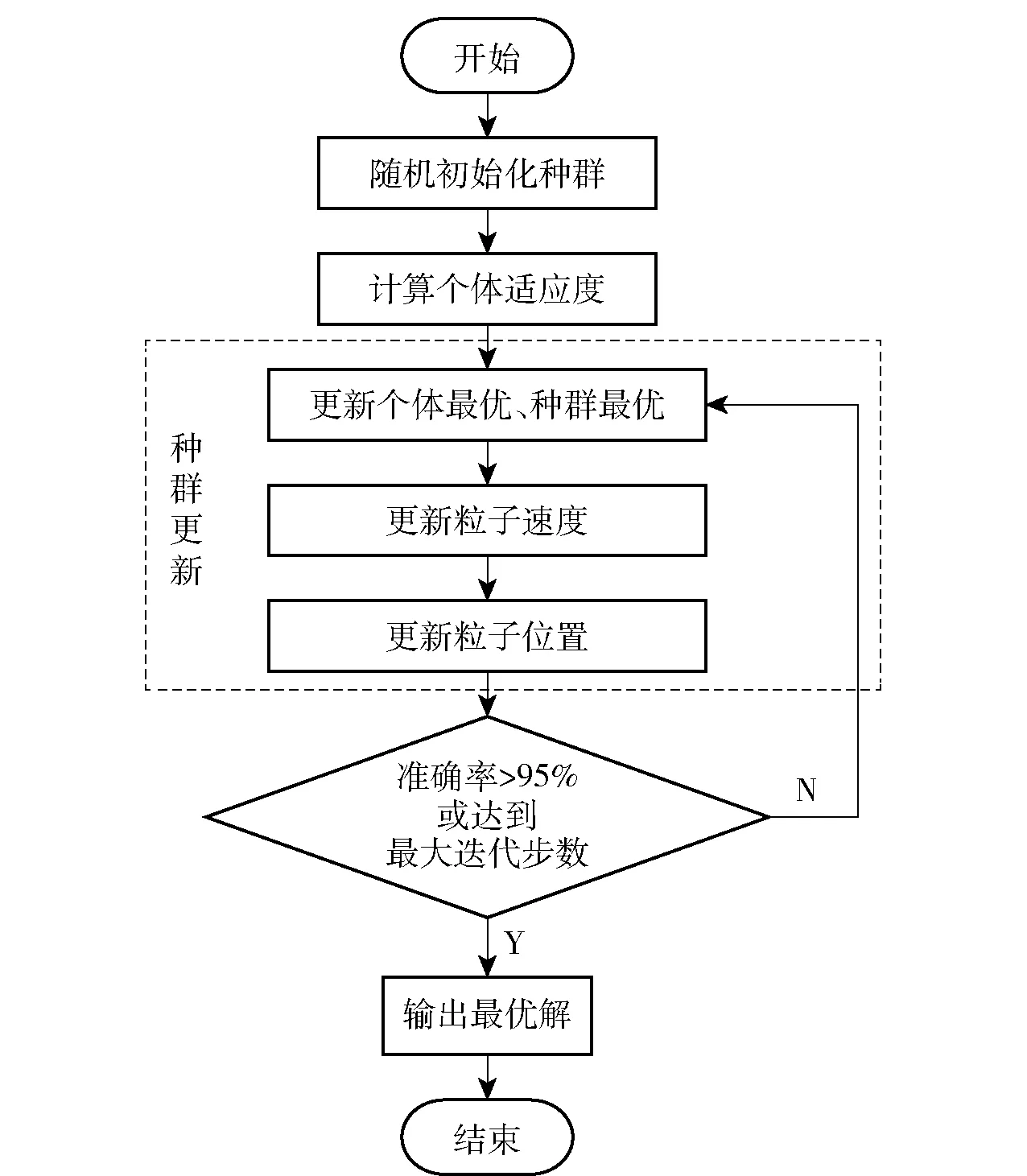
图8 PSO算法流程图Fig.8 Flow chart of PSO algorithm
4 仿真验证
4.1 威胁评估模型仿真验证与分析
411 模型动态适应性验证
威胁评估模型中的初始权重采用多专家加权确定,专家可以先给出一个模糊数作为灰数的中心,随后给出不确定性的大小,汇总时按照专家的专业程度、经验年限等因素,加权求权重的均值,分别加权确定灰数的中心数和不确定度。需要注意的是,灰数的上下限要在[-1,1]区间内。最终确定初始关联权值矩阵为

为确定(9)式~(12)式中调节系数的最佳取值,并验证模型在复杂多变的外部环境中的动态适应能力,设置5组不同的战场环境条件,分别发生在~时刻,设置1组最具代表性的输入⊗={⊗~⊗},如表4所示。5组时刻的外部环境有相对优劣,通过常识可知环境条件越恶劣,越不利于敌方目标飞机入侵,即敌方目标的威胁程度越低。

表4 不同时刻的节点值设定Tab.4 Vk value setting at different time
先将输入⊗={⊗~⊗}和、时刻的值代入模型,依次将权重调节系数,设置为02、04、06和08,记录模型推理结果⊗的不确定度和白化值,如图9所示。

图9 不同时刻和调节系数下推理结果对比Fig.9 Comparison of reasoning results in the case of different times and adjustment coefficients
由于时刻的环境更加复杂,外部控制节点的绝对值更大。由图9可以看出:外部环境越复杂,权重调节系数,对输出结果的影响越明显;,越大,模型对环境变化的敏感度越高,动态适应性越强;随着模型动态适应性的提高,推理结果的不确定性也在增加,故在权重调节系数的选取上要权衡模型的动态适应力和推理结果的不确定性。
由权重调整规则可知,当多个控制节点同时对一个权值⊗,起作用时,只选取使该权值变化最大的。为兼顾模型对环境的动态适应性和尽可能小的不确定性,可以根据专家知识对环境节点重要性的判断,为更重要的外部控制节点设置更大的权重调节系数,,在该原则基础上经过多次仿真,最终确定权重调节系数如表5所示。

表5 权值调节系数Tab.5 Weight adjustment coefficient
采用最终确定的调节系数来验证模型的动态适应性,在同一组输入⊗={⊗,…,⊗}下分别代入~的外部环境变量,得到输出节点⊗的不确定性和白化值如图10所示。由图10可以看出,对于同一组输入,模型在不同时刻下的输出不确定性和白化值都有所变化,威胁评估的结果也符合“环境越恶劣,敌方飞机目标入侵难度越大,威胁越低”的规律。
412 模型有效性验证
为了验证威胁评估模型的动态不确定性推理能力,在时刻下设置5组输入,如表6所示。
第1组输入的每个节点的灰度都为0,即第1组数据节点值都是精确值,用一组上下限相等的灰数表示;第2组中只有一个具有不确定性输入的节点⊗,且灰度为02;第3组中有3个节点的输入具有不确定性;第4组输入与第3组类似,但节点⊗的灰度为1,表示目标侦察能力数据缺失,模拟不完备信息下的威胁评估。第5组与第3组对比,用灰数表示另外3个属性。5组数据基本涵盖了各种类型目标属性的情况,根据表6定性分析可知:

图10 不同时刻模型输出对比Fig.10 Comparison of model outputs at different times

表6 不同时刻具有不同不确定性的输入与模型输出Tab.6 Input and output of model with different uncertainties at different times
1)第1组~第4组目标各项参数相差不大,但数据的不确定度逐渐增加,分析可知威胁评估的白化结果应该大致相等且不确定性程度排序为:第1组<第2组<第3组<第4组。
2)第4组数据目标属性⊗的灰度为1,推理结果的不确定度应该为5组数据中最大。
3)比较第3组和第5组,由于第5组的目标能力参数整体比第3组高,经过白化后的第5组的目标威胁程度应当大于第3组。
5组仿真数据的威胁评估仿真验证结果如图11所示。灰色色块长度代表模型评估得到的目标威胁程度的灰度,数字分别为威胁程度的上、下限值。

图11 基于DFGCM的威胁评估仿真结果Fig.11 Simulated results of threat assessment based on DFGCM
表6和图11表明:
1)前3组数据的评估结果白化值大致相等,但不确定度依次增加,符合预期效果。
2)即使第4组仿真数据中对评估敌方威胁程度的探测能力参数完全未知,威胁评估模型仍能输出较为合理的结果,但结果的不确定性会较大。
3)第3组和第5组的评估结果白化后的区分度明显,可用于比较不同目标的威胁程度。
综合来看,基于DFGCM的目标威胁评估模型有效且具备动态适应能力,能够对不同战场环境下的不同目标进行较为合理的威胁评估。
为进一步验证DFGCM模型评估的有效性和可信性,对于表6中的5组数据,采用比较成熟的TOPSIS法进行评估。由于TOPSIS法处理的是精确值,评估之前需要对表6中的灰数进行处理,分别采取3种方法对灰数进行处理:取灰数的下限、取灰数的上限、取灰数的白化值。例如,对于第2组数据的⊗=[0.5,0.7],3种方法对其处理后的精确值分别为0.5、0.7、0.61(白化结果保留两位小数),将表6中的数据处理之后作为归一化后的决策矩阵。由于TOPSIS法不考虑属性之间的相互影响,每个属性有对应的权重,与本文方法不同的是TOPSIS法各属性的权重之和为1,只保留图5模型中属性节点⊗~⊗指向输出节点⊗的权重⊗~⊗进行白化,并用(18)式进行归一化,得到6个属性的相对权重:

(18)
得到决策矩阵和权重之后分别计算正、负理想解并计算综合评价值,3种灰数处理方式下的综合评价值如表7所示(结果保留4位小数)。

表7 TOPSIS法评估结果对比Tab.7 Comparison of TOPSIS evaluated results
由表7可以看出对灰数采取的处理方式不同,最终的评估结果相差较大:1)取灰数下限值时,前3组数据得到的综合评价值很接近;2)取灰数上限值时,第1组数据由于各项指标都为5组数据中最小,因此综合评价值为0,5组数据不管是综合评价值还是其排序,都与取灰数下限的处理方法相差较大,表明采用TOPSIS法评价时,对于灰数的处理不宜简单地取其上限值或者下限值;3)将灰数白化后再用TOPSIS法进行评估,可以看出数据有了明显的区分度,威胁排序的结果为:第1组<第2组<第4组<第3组<第5组。
由此可见,基于DFGCM的威胁评估推理结果白化值的排序与TOPSIS法的排序结果一致,侧面再次验证了威胁评估DFGCM模型的有效性。与TOPSIS法不同的是,DFGCM模型考虑了节点之间的相互影响,更关注动态、不确定性环境下威胁值的量化,在目标参数不准确或缺失情况下仍能进行有效评估;TOPSIS法更关注不同目标威胁程度的排序,得到的综合评价值仅作为判断相对大小的依据,对于单个目标无法进行威胁值的量化评估。
4.2 目标意图预测模型仿真验证与分析
采用《2015年全国研究生数学建模竞赛A题》和文献[34]提供的目标意图预测样本数据,构建包含41组数据的学习样本库,如表8所示。使用PSO算法对其中的26组数据样本进行学习,其余15组数据样本经过不确定性处理后用于测试验证。由于FGCM模型处理的数据为灰数,对于表8中的精确数,将其归一化后扩展为上、下限相等的灰数形式,再与灰数形式的权值一起参与推理运算。例如,某组数据的某一项参数归一化后为0.6,则扩展为灰数形式的[0.6,0.6],再根据(6)式和(7)式的灰数运算法则参与运算。根据(6)式和(7)式进行灰数(区间数)的加法和乘法运算示例如下:
[0.3,0.5]+[0.6,0.6]=
[0.3+0.6,0.5+0.6]=[0.9,1.1];
[0.3,0.6]×[0.6,0.6]=
[min (0.3×0.6,0.3×0.6,0.6×0.6,0.6×0.6),
max (0.3×0.6,0.3×0.6,0.6×0.6,0.6×0.6)]=
[min (0.18,0.18,0.36,0.36),
max (0.18,0.18,0.36,0.36)]=
[0.18,0.36]
FGCM推理公式(3)式中的矩阵乘法根据上述法则进行运算,得到新的节点灰数值之后用sigmoid函数归一化到[0,1]之间,进而参与后续运算。
4.2.1 模型不确定性推理能力验证
为验证学习算法的有效性和模型不确定性推理能力,按第3节设计的PSO算法学习权重矩阵,将学习得到的FGCM模型用于后续的仿真验证。对于样本的学习,PSO算法的步骤如下:

将威胁值和归一化之后的各项数据赋值给对应的节点⊗~⊗;分别将种群中每个个体赋值给权重矩阵。
用(3)式的FGCM推理公式,分别计算每个权重矩阵在26组训练数据下输出节点⊗的值,并用(8)式、(13)式进行白化。

表8 目标意图预测模型学习数据样本库Tab.8 Learning data sample database of target intention prediction model
根据白化值和图6中的阈值~判断是否分类正确,根据(14)式计算每个权重矩阵下26组数据意图识别的准确率;根据(15)式计算每个权重矩阵下26组数据输出结果的平均不确定度。
选择准确率高、平均不确定度小的权重矩阵作为当前最优个体,根据(17)式、(18)式对个体进行更新,形成新的种群。
得到更新后的种群后转到步骤2,循环执行步骤2~步骤6,直到满足终止迭代条件。
设置种群大小为500,PSO算法的惯性因子取为1,学习因子取为2,为防止粒子更新步长过大,设置粒子最大速度为0.1。设置终止条件为分类准确率达到95%以上或达到最大迭代步数10 000步。在学习过程中,对于超出限定范围的个体进行重新初始化。
仿真结果表明,26组训练数据的分类准确率为96.15%,模型推理结果的平均灰度为0.60。为了直观地表现学习结果,将目标意图预测FGCM模型的权值可视化,如图12所示。图12中,箭头的粗细代表关联权值白化后绝对值的大小,箭头越粗,表示关联权值越大;箭头的颜色表示关联权值的灰度,颜色越深,表示该关联权值的灰度越小;箭头的虚实表示灰数权值白化后的符号,实线表示正值,虚线表示负值。

图12 PSO算法的学习结果Fig.12 Learning result of PSO algorithm
训练完成的模型在15组数据的测试集上准确率为93.33%,为了验证模型的不确定性推理能力,模拟真实情况下目标某些数据缺失或不准确的情况,分别对测试集中归一化后的目标参数做一定程度的不确定性处理。例如,某组数据中目标的水平速度经过归一化后为0.6,表示为灰数形式为[0.6,0.6],对其进行单侧灰度为10%的不确定性处理,即对灰数下限减小10%,上限增加10%,处理结果为[0.54,0.66],将此作为目标参数输入FGCM模型进行推理,验证是否预测准确。分别对测试集数据中节点⊗、⊗、⊗做10%、20%、30%、40%的不确定性处理后输入意图预测FGCM模型,统计测试集上的准确率如图13所示。

图13 不确定性数据下模型预测能力Fig.13 Model prediction ability for uncertain data
由图13可以看出对节点进行不确定性处理,测试集上的预测准确率会受到一定程度的影响:
1)随着不同节点不确定性的增加,模型整体的预测准确率呈下降趋势。但当节点不确定性较小(10%,20%)时,仍能取得较高的预测准确率,即模型具备一定的不确定性处理能力,符合设计预期。
2)节点⊗和⊗的不确定性大到一定程度,预测准确率下降明显,而节点⊗的不确定性对预测准确率影响不大。结合图12中的学习结果可以发现,节点不确定性对预测准确率的影响程度,与其对应的权值大小相关。
综上分析可知,意图预测FGCM模型允许目标参数存在一定的不确定性,在无法获得目标某项准确参数时,意图预测的结果仍然具有较高的参考价值。
4.2.2 模型预测准确率对比
将本文FGCM模型结合PSO算法(FGCM模型+PSO算法)的意图预测方法与文献[28]中基于神经网络模型和Adam算法(神经网络模型+Adam算法)的意图预测方法进行对比分析。依据文献[28]中的方法设置神经网络模型的结构为输入层7个节点,隐含层32个节点,输出层4个节点,采用交叉熵作为误差函数,学习算法采用Adam算法,其各参数设置与文献[28]保持一致,同样使用本文中的训练集和测试集,经过8 000步学习之后,意图预测准确率对比情况如图14所示。

图14 意图预测准确率对比Fig.14 Comparison of intention prediction accuracies
由图14可以看出,神经网络模型+Adam算法的方法在训练集表现非常好,预测准确率达到100%,而测试集的准确率有了明显下降,为86.67%。这种现象一般被称为过拟合,即把训练样本自身的一些特点当作了所有潜在样本都会具有的一般性质,导致模型的泛化性能下降。过拟合越严重,学习得到的模型在面对新的样本时表现越差。
图14中两种方法都存在一定的过拟合现象,但可以发现:
1) FGCM模型+PSO算法在训练集预测准确率上相对较低,但测试集准确率高于神经网络模型+Adam算法;
2) FGCM模型+PSO算法的训练集预测准确率和测试集准确率之间的差小于神经网络+Adam,表明FGCM模型+PSO算法可以在一定程度上降低过拟合现象。
综合分析本文目标意图预测方法与基于神经网络的方法的特点如下:
1) FGCM模型综合了灰数理论,将权值设置为灰数,使得模型在无法获得目标属性精确数值的情况下可以进行推理,模型输出结果包含的不确定度能从侧面反映意图预测的好坏,模型结构的确定也可以利用一定程度的先验知识;
2) PSO算法能够得到预测准确率和泛化能力都不错的权值参数,但作为种群演化类算法,由于需要一定规模的个体并行求解,其学习过程对计算机性能要求更高,学习时间也更长;
3)神经网络在数据都转换为精确值的情况下可以达到非常高的训练精度,且基于梯度下降原理的Adam模型能够在很短的时间内完成8 000步的学习,模型在测试集上也有不错的预测准确率,但过拟合现象相对严重一些。正如前文所述,神经网络在有大量数据支撑的情况下可以达到很高的拟合精度,适应于数据准确且容易获得的场景,对于不确定数据的处理能力较弱。另外,由于神经网络隐含层节点无明确含义,隐含层的层数和节点数的确定需要通过不断仿真进行试探,以达到最好的预测效果。
5 结论
本文基于态势觉察、态势理解和态势预测3层SA建模框架,提出了自上而下任务驱动方式的态势觉察建模思路,以目标威胁评估和意图预测为重点研究对象开展了态势理解和态势预测的建模工作。得出主要结论如下:
1) 威胁评估DFGCM模型能够适应动态、复杂的战场环境,威胁排序结果与经典的TOPSIS法一致,且能够在态势元素不准确或丢失的情况下对单一目标进行合理的威胁量化评估。
2) 基于FGCM模型+PSO算法的目标意图预测模型取得了理想的训练和测试准确率,与基于神经网络的模型相比,FGCM模型+PSO算法的意图预测模型在防止过拟合方面有更好的表现。
需要指出的是,本文为便于建模工作的开展,特定选择了态势理解层和态势预测层中最受关注的威胁评估和目标意图预测两个问题开展了建模方法的研究,可为同行提供学术启发和方法参考。由于研究内容相对具体,本文所提出的建模方法在通用性和适用面上相对有限,如何将其扩展并应用到更大范围的指挥控制层面,还需要在后续工作中进一步研究。

