有载分接开关驱动轴转动位置的闭环反馈抗扰控制策略

有载分接开关是特高压直流输电工程最关键、最核心的设备特高压换流变中的关键组件之一

。通过有载分接开关的调整,换流变可以维持运行中阀侧直流电压恒定不变,保证直流系统的安全经济运行,也可以实现特高压直流输电系统降压运行

。国内外企业、科研单位也研发出了机械式、电力电子式、混合式等形式的有载分接开关

。各类有载分接开关主要由切换芯子、分接选择器、电动机构、油室和安全保护装置等部件组成

。有载分接开关遵循先选择后切换的基本原则完成每次工作,由分接选择器选择好要切换的挡位,再由切换芯子完成不中断负载电流的情况下切换电流,分接选择器和切换芯子的完成这一切换动作是由基于电动机构的驱动系统来进行驱动控制的,并且需要实现双向的驱动控制

。电动机构的输出轴通过联轴器、换向齿轮、减速器等结构连接至有载分接开关的输入驱动轴。有关有载分接开关故障分析的工作表明电动机构是较容易产生故障的主要部件之一

。有载分接开关是特高压换流变中经常动作部件,因此驱动系统的平稳、准确的驱动控制也是特高压直流输电工程稳定安全运转的前提。

电动机构包括电动机、传动换向齿轮盒、传动轴和手动操作机构等控制和传动机构,其共同组成了有载分接开关的驱动系统,驱动系统的操作机构一般安装在变压器油箱侧壁上,通过电动、手动、遥控和自动调压装置控制电动机,借助传动换向齿轮盒和传动轴可实现将电动机的转矩传至分接选择器和切换芯子

。虽然目前的有载分接开关电动机构通过微处理器技术、单片机技术、控制电路设计等方法已经向着智能化、模块化发展,但是其仍是一种开环控制方法,即电动机收到控制信号后,在不受外界任何干扰和中断情况下完成指定动作后停止

。随着现代控制理论的发展,研究人员开发设计了多种闭环反馈控制策略并成功应用在各类电动机操作中,达到了更好的控制效果

。因此本文考虑针对有载分接开关电动机构工作特点,设计适合的驱动系统闭环反馈控制方法,来使其能够实现更为平稳、准确的驱动控制。

5)引入“实景仿真实验+互联网”教学模式，可使学生的学习行为由被动变成主动，由“灌输式学习”为主的教学模式变成“按需学习”及“自由式学习”为主的以全面提升学生实践能力的全新教学模式.

设计有载分接开关驱动电机的闭环反馈控制需要考虑到电机驱动切换芯子和分接选择器时的扭矩变化、切换芯子释能时的负载冲击、齿轮正反转间隙误差等非线性因素,这些非线性因素会造成驱动电机控制系统的数学模型不精确。Han设计并提出了跟踪微分器、扩张状态观测器,并考虑两者产生信号的非线性反馈组合,最终整合提出的一种不依赖被控对象具体精确数学模型控制算法

。该算法在液压控制系统

、气动控制系统

、机器人控制系统

等多种应用中得到成功的验证,尤其是该算法已经在多种电机控制问题中展现出较强的优势

。因此自抗扰控制算法可以作为有载分接开关驱动电机的理论基础,但是仍需针对有载分接开关自身运动的特点进行算法上设计研究。

本文针对有载分接开关电动机构作用下驱动系统的闭环反馈控制问题,梳理了驱动系统通过闭环反馈期望得到的控制效果,进行了驱动系统轨迹跟踪误差的动态系统建模,利用跟踪微分器对有载分接开关驱动系统输出的期望值进行了期望轨迹计算,基于动态系统模型设计了扩张状态观测器和误差反馈控制器。最后通过仿真验证了所提控制算法的有效性,这为有载分接开关驱动系统闭环反馈控制提供了理论基础。

1 驱动系统控制问题描述

1.1 有载分接开关控制需求

根据国内外主要有载分接开关生成设备的实际工作情况,在有载分接开关在电动机构的驱动下实现一次电压调节动作可以分为4个阶段:首先电机和驱动轴均从初始时刻和初始位置开始旋转进行切换芯子储能动作和分接选择器极性选择动作;在选择器选择动作完成后通过间歇机构使其保持所需极性选择,并且切换芯子继续储能直到释能开始;切换芯子储能机构短时间内完成释能带动切换开关实现变压器有载切换,在切换芯子释能期间,电机和驱动轴在持续运动;驱动轴在电机作用下继续驱动切换芯子储能机构直到预定的终止位置,也是下次切换的起始位置。

图1展示了有载分接开关在变压器中的一个应用示意简图。如图1所示,有载分接开关的电机控制箱一般安装在变压器箱壁上,通过控制电机经垂直和水平传动轴、齿轮减速换向箱等结构来将电机转矩传递到有载分接开关驱动切换芯子和分接选择器的驱动轴

。切换芯子和分接选择器是由同一根驱动轴来实现驱动的,驱动轴同时驱动切换芯子的快速机构和分接选择器的极性选择

。

在有载分接开关实现一次切换运动中,驱动轴需要在设定的时间内平稳、准确的驱动切换芯子和分接选择器中的机构达到期望的角度。在运动中,驱动轴会受到切换芯子和分接选择器在不同动作顺序下的变化负载,而且在切换芯子释能动作时驱动轴会受到冲击载荷的影响。此外,根据变压器调压需求,有载分接开关会有不同方向的动作要求,在换向时由于齿轮间隙等因素会造成电机期望驱动角度和驱动轴实际运动角度不一致,进而导致起始或终止位置存在误差。为了有载分接开关安全稳定的工作,考虑其控制工程中的动作时序和需求,本文拟对分接开关驱动动态系统进行建模,将驱动轴的旋转角度进行反馈调节电机的控制量,实现驱动轴的平稳准确运动,为有载分接开关驱动系统提供一种闭环反馈控制方法的理论基础。

1.2 驱动系统动态系统建模

有载分接开关的驱动电机安装在变压器外壁的电机箱中,根据现有国内外有载分接开关电动机构专利,目前电动机构中应用的是步进电机

。因此本文以二相混合式步进电机为例,对有载分接开关驱动系统进行动态系统建模。基于研究者对步进电机的数模型的推导

,二相混合式步进电机数学表达式为

(1)

式中:

(

)、

(

)为电机轴的角位移和角速度;

(

)、

(

)为电机的两相线圈电流;

为电机转子系统的转动惯量;

为扭矩常数;

为电机的黏滞摩擦系数;

(

)为负载转矩;

(

)、

(

)为电机的两相输入电压;

、

为各相绕组的电阻和电感;

为电机转子齿数。

2.2.4 径流补给 根据《内蒙古自治区水资源及其开发利用调查评价》，河套灌区多年平均年径流深仅为5 mm。且周边地势平坦，渠系复杂纵横交错，径流量极小，补给量只占淖尔春季蓄水量的0.2%～0.3%可忽略不计。

设有载分接开关在电机作用下的驱动轴的转动角度及角速度为

(

)、

(

),由于电机输出到驱动轴运动间存在各种干扰,驱动轴转动角速度与电机输出轴的角速度间存在如下关系

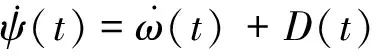
(2)

式中

(

)为时变的各类未知干扰力。

针对有载分接开关驱动系统,定义误差变量

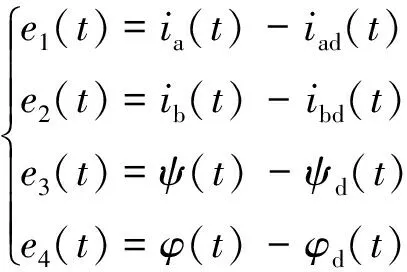
(3)

式中:

(

)、

(

)、

(

)和

(

)为期望变量运动轨迹。通过微分平坦理论

,在光滑的电流期望轨迹

(

)和位置期望轨迹

(

)确定时,可以得到其他期望变量的轨迹,即

共产党人的哲学，永远都是在艰困中开拓，在阻难中前行，在实现民族复兴、人民幸福的道路上，我们的哲理永远只有一个，那就是坚定信念，奋发进取，矢志不移地奋进在中国特色社会主义的大道上！而中国特色社会主义所强化和凸显的，则也正是我们雄威壮美、如钢似铁的道路自信！

(4)

保证档案资源横向纵向交流畅通，应该结合信息技术的发展，不断的通过加密技术、规范的数字化技术、数据分析技术等进行全面的管理，核实。从而满足在大数据时代下，企业档案管理的安全性，实现服务多元化，管理高效化。

(5)

式中:

(

)、

(

)为分接开关电动机构的期望控制变量轨迹,其表达式可由期望轨迹

(

)、

(

)表示

(6)

通过微分平坦性

,设置误差动态控制系统(5)的两个平坦输出为误差变量

(

)和

(

),即电流

(

)和驱动轴转动角度

(

)的跟踪误差。通过表达式(1)～(6),分接开关驱动误差动态系统可进一步表示为

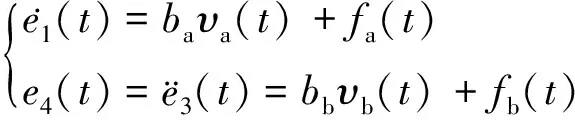
(7)

式中:

(8)

(

)=

(

(

)

(

)+

(

)

(

)+

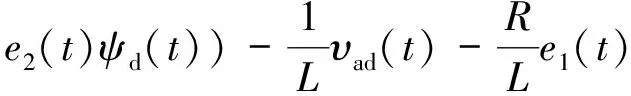
(9)

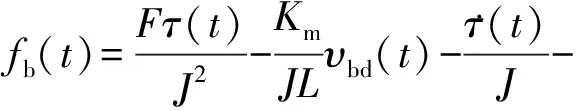
(10)

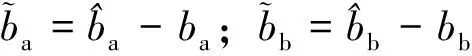
(11)

(12)

(13)

2 闭环反馈控制算法设计

针对有载分接开关驱动轴的驱动误差动态扩张系统,本文提出了基于跟踪微分器和线性扩张状态观测器的非线性误差反馈抗扰控制策略。本文设计的闭环反馈抗扰控制算法的示意图如图2所示。

在这一种类型的朗读中，由于对单词视觉刺激与语音形式之间联系的熟知，学习者很容易就能够获得语言的语音物质外壳而达到朗读的标准。然而，语言的使用是以意义为中介的，朗读必须有意义的介入，必须建立在意义理解的基础之上。因而这种类型的朗读需要学习这有意识地对其进行意义的加工和构建，不能满足于简单地能读出来的望字出声。如果学习者的朗读仅停留在这个层面，则也基本上对于学习的促进意义不大。更好的做法是：在能够对书面材料正确朗读之后，要在朗读过程有意识地对其意义进行提取、加工，从而逐渐在声音加工和意义加工之间进行一种匹配，加强声音与意义之间的互动，这样能更好地促进第二语言学习听力与口语能力的提高。

由上文对有载分接开关控制需求分析可知,有载分接开关驱动轴需要在设定的时间内达到设定的角度,跟踪微分器可以针对有载分接开关驱动轴角度运动轨迹安排平滑的过渡过程,得到期望信号的跟踪信号,并且可以通过调整参数达到设定时间的需求。设有载分接开关驱动轴的期望达到的转动角度为

,驱动电机的线圈期望电流值为

,为得到在设定时间段内光滑的电流期望轨迹

(

)和驱动轴位置期望轨迹

(

),本文设计如下所示的两个二阶跟踪微分器

2.1 跟踪微分器

作为发展的主要动力，改革是所有事物走向更高水平和层次的前提。同样，对于教学，改革是为了提升教学质量，为培养学生打造更好的平台。在新课程背景下，要求小学信息技术教师培养学生信息素养和实践操作能力，而创新小学信息技术教育正好符合现下教学改革发展。

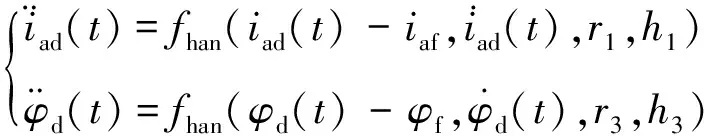
(14)

式中:

(

)、

(

)分别为

、

的跟踪信号,此外跟踪微分器还可以得到跟踪信号的微分信号;

、

为两个跟踪微分器的滤波因子,跟踪微分器的滤波能力与滤波因子呈正相关的关系,

、

为两个跟踪微分器的速度因子,跟踪微分器的跟踪速度与速度因子呈正相关的关系。跟踪微分器中非线性函数

(

(

),

(

),

,

)的表达式

为

(15)

根据误差变量可以进一步得到分接开关驱动系统的误差动态控制系统

在欠发达省份，农业是主要用水部门，水的利用效率和效益较低。但由于正处在加快发展阶段，水问题也日益复杂严峻。

2.3.1 不良反应总发生率 纳入10个研究［6‐7，9‐11，13‐17］，各研究间为同质性（P=0.37，I2=8%），采

2.2 扩张状态观测器

本文考虑有载分接开关驱动系统只有驱动轴的转动角度

(

)和驱动电机的线圈电流

(

)可以被测量得到,即有载分接开关驱动误差动态扩张系统(13)中只有状态量

(

)和

(

)可以被测量得到。为实现有载分接开关驱动系统平稳准确的控制需可设计合适的观测器去估计系统中的未知状态量。自抗扰控制算法中的扩张状态观测器可以仅用较少的测量值去估计观测出系统的未知状态,尤其是系统中的总和扰动所扩张的状态量

。因此,本文针对分接开关驱动误差动态扩张系统(13),设计的二阶和四阶线性扩张状态观测器为

(16)

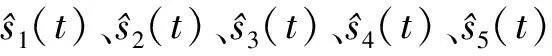
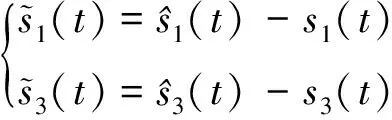
(17)

在所设计的扩张状态观测器(16)中,

、

、

、

、

和

为可调参数,通过调整合适的参数得到期望的观测器估计效果,线性扩张状态观测器的优势在于参数正定方便,便于实际应用。美国克利夫兰大学的高志强教授基于特征方程理想稳定形式提出了一种“带宽法”的线性扩张状态观测器的调参方法

,针对本文所应用的二阶和四阶扩张状态观测器,所对应的特征方程为

(18)

为得到扩张状态观测器稳定的估计效果,可将两个特征方程配置为(

+

)

和(

+

)

,其中

和

是有载分接开关驱动误差系统(13)的系统带宽。在特征方程的配置下,两个扩张状态观测器的6个可调参数可设置为

(19)

在有载分接开关驱动系统模型参数设置下,本文所设计闭环反馈控制算法中的控制参数调整如表2所示。

2.3 误差反馈控制器

本文针对分接开关驱动误差动态扩张系统(13),在两个跟踪微分器和两个扩张状态观测器的基础上,可以得到分接开关驱动系统的期望值和实际值间的误差值,通过误差值间的线性或非线性的组合反馈可以得到不同的控制效果

,这在自抗扰控制算法的一些应用文章中也得到了广泛的验证,本文针对所得到的误差值,设计误差反馈控制器

(20)

式中:

、

、

和

为大于0的可调误差反馈控制器参数;非线性反馈调节函数fal(

(

),

,

)可以通过调节函数中的参数

和

使其发挥“大误差,小增益;小误差,大增益”的特点,更利于有载分接开关的工程应用,起到更佳的控制效果

。非线性反馈调节函数fal(

(

),

,

)的函数表达式为

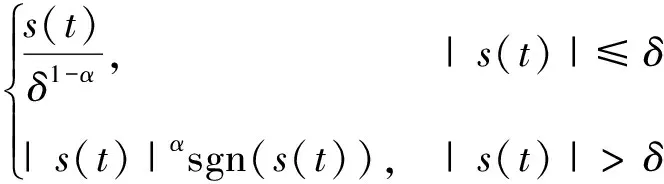
(21)

式中:0<

<1为非线性函数中的调节参数,通过调节可实现不同程度的“大误差,小增益;小误差,大增益”特性;

>0表示非线性函数中的线性段,具有线性段的目的是避免在“小误差,大增益”产生高频的抖振影响控制效果。

3 仿真验证

为了验证本文所提的闭环反馈控制方法对有载分接开关驱动系统控制的有效性,本文利用Matlab仿真软件,通过对有载分接开关驱动系统模型参数设置、控制算法参数调整对所提闭环反馈控制算法进行了仿真验证。

3.1 仿真设置

以文献[22]中给定的步进电机模型参数为参考,本文对有载分接开关驱动系统的主要参数设置如表1所示。

静电分离法是70年代兴起的液固分离技术，原理是当油浆流经填料床层时，催化油浆中的固体微粒在高压电场作用下被极化带上电荷，从而被填料吸附，达到净化油浆的目的。最早的静电分离器是由美国的海湾石油公司设计研发制造，美国的阿瑟港石油公司用于工业应用。之后国内很多研究机构做了大量的研究和技术改进，赵娜[3]等人在Caoqing[4]，Abidin[5]等人的研究基础上自制静电分离装置，通过三级静电分离对重油催化油浆的固体颗粒物脱除率高达99%。虽然静电分离法脱除率高，但该法对10μm以下的颗粒物分离效果显著，且所需设备复杂，分离效果受油浆性质、操作条件影响，因此在我国还未实现工业应用。

根据前文有载分接开关控制需求所述,有载分接开关驱动系统在实现一次切换任务时,会存在4个阶段,有载分接开关驱动系统中的负载转矩

(

)也是随着驱动轴在这4个阶段中的转动角度而变化的,并且会存在负载转矩突然减小的情况,针对有载分接开关驱动系统所面临的实际工况条件,本文在仿真中设置负载转矩函数为

(22)

此外,值得注意的是,实际有载分接开关驱动系统在运行时的工况较为复杂,动态系统中的未知干扰也较为复杂,在本小节中,为验证所提控制算法的有效性,有载分接开关驱动系统中的未知干扰

(

)假设设置为

(

)=0

5sin(

)

(23)

根据式(19),本文所应用的扩张状态观测器可以通过调整参数

和

实现状态估计。

3.2 仿真结果

根据文献[22]和[26],为了使焦耳损耗最小化和电机转矩最大化,选择电流期望值为

=0。根据有载分接开关选择和储能切换需求,设置驱动轴的期望转动角度为

=180°。通过跟踪微分器式(14),得到如图3所示设定时间段内光滑的电流期望轨迹

(

)和驱动轴位置期望轨迹

(

)。

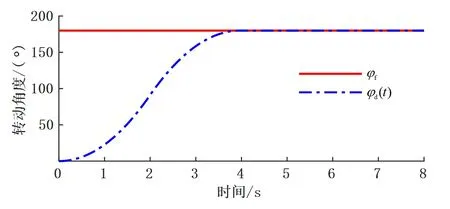
在所设计控制方法及参数设置下,有载分接开关驱动轴的转动角度对期望轨迹的跟踪效果如图4所示。根据仿真结果可以看出,在所提控制方法下,有载分接开关驱动轴可以快速、光滑、无超调的跟踪上所计算得到的期望轨迹。

综上所述，运用多排的螺旋CT肺小结节来进行分析，对与早期的肺癌中，其诊断的价值较高，对于早期的肺癌筛查中，临床上值得使用与推广。

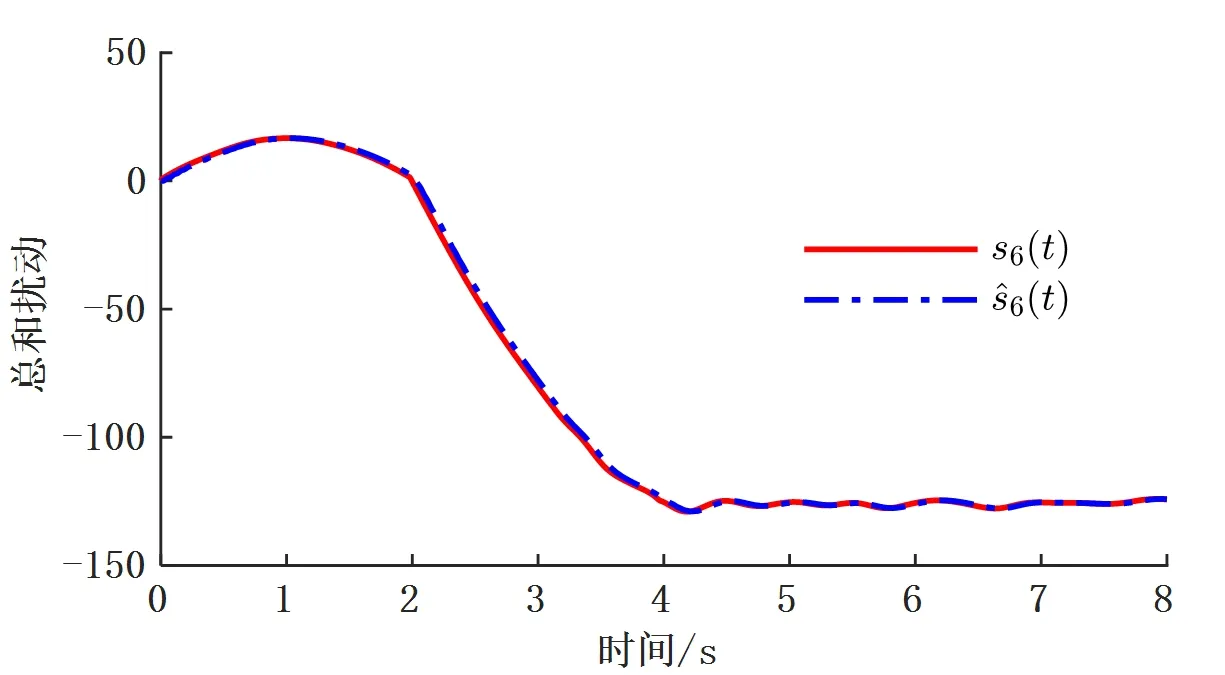
本文所应用扩张状态观测器对总和扰动的观测效果如图5所示,根据图5所示的仿真估计结果,本文所设计的二阶和四阶扩张状态观测器均能有效的跟踪上总和扰动,因此所估计的总和扰动也可以有效在误差反馈控制器中进行补偿。

吕凌子极具耐心地听她发完牢骚，说，发票复印件我会催物业公司的陈主任明天给送过去，这会1402号业主也不知道在不在家，我马上去看看，要是在的话，麻烦你再派人来一趟。

为对比本文所提控制算法对有载分接开关驱动系统驱动轴的闭环反馈控制效果,与传统PID控制算法进行了对比仿真。即在本文所设计的跟踪微分器安排的过渡过程下,针对分接开关驱动误差动态扩张系统(9),设计的PID反馈控制器为

综上所述，在建筑工程行业建设水平不断提升的背景下，混凝土浇筑技术的应用重要性愈发突出，这不仅使混凝土建筑施工技术的施工要求更为复杂，也在一定程度上规范了混凝土浇筑施工技术的实施水平。为此，为避免混凝土浇筑施工技术出现质量不合格的情况，更好达到现阶段建筑行业对混凝土浇筑施工技术提出的要求，需要在进行混凝土浇筑施工技术运用时，根据建筑工程的实际建设需求，合理选择混凝土浇筑施工技术方式进行施工，以使得建筑工程的混凝土浇筑质量能够得到有效保障。

(24)

式中

、

、

、

、

和

为控制器增益,在仿真对比中设置为

=-0

1、

=-0

1、

=-0

1、

=-40、

=-0

8和

=-100。对比仿真结果如图6所示,其中

(

)和

(

)分别为PID控制算法下的有载分接开关驱动轴的转动位置轨迹和跟踪误差,与传统PID控制策略相比,本文所提控制方法将有载分接开关驱动轴闭环反馈控制下位置误差减小了85%。

4 结 论

本文针对有载分接开关在实现切换工作时驱动轴的实际应用需求,在步进电机数学模型基础上推导了有载分接开关驱动轴的位置误差动态系统,通过动态系统设计了跟踪微分器、扩张状态观测器和误差反馈控制器所组成的闭环反馈控制策略。得到以下结论:

万用表放置在电阻块中，其范围取决于所测量的电解电容器的电容和耐电压的大小。测量小容量耐高压电解电容时，测量范围应设在Rx10kW块内，测量大容量耐低压电解电容时，测量范围应设在RxlkW块内。观察充电电流的大小、放电的持续时间(针返回的速度)以及针末端指示的电阻。确定电解电容器质量的方法如下：

(1)跟踪微分器的设计可计算分接开关驱动轴位置信号的光滑跟踪信号,进而可通过调节参数来控制驱动轴位置轨迹的过渡过程;

(2)扩张状态观测器的设计可以有效估计出分接开关驱动轴期望位置误差动态系统中的未知状态及运动中受到的总和扰动值;

(3)仿真结果表明本文所提的控制策略可实现有载分接开关驱动轴的期望位置控制,与传统PID控制策略相比,有载分接开关驱动轴闭环反馈控制下转动位置误差减小了85%。

:

[1] 官澜, 李光范, 李博, 等. 我国特高压电力变压器研制技术及发展 [J]. 变压器, 2014, 51(8): 28-33.

GUAN Lan, LI Guangfan, LI Bo, et al. Manufacture technology and development of UHV power transformer in China [J]. Transformer, 2014, 51(8): 28-33.

[2] 刘雪丽, 李金忠, 高飞, 等. ±800 kV换流变压器用真空式有载分接开关关键技术研究 [J]. 中国电机工程学报, 2016, 36(19): 5350-5356.

LIU Xueli, LI Jinzhong, GAO Fei, et al. Key technology research for vacuum type on-load tap-changer of ±800 kV direct current convertor transformers [J]. Proceedings of the CSEE, 2016, 36(19): 5350-5356.

[3] 张磊, 陈梁远, 余长厅, 等. 变压器有载分接开关运行分析及探讨 [J]. 广西电力, 2020, 43(5): 32-35.

ZHANG Lei, CHEN Liangyuan, YU Changting, et al. Analysis and discussion on operation of the transformer on-load tap-changer [J]. Guangxi Electric Power, 2020, 43(5): 32-35.

[4] 高飞, 李金忠, 张书琦. 新型变压器有载分接开关综述 [J]. 电工电气, 2013(10): 1-5.

GAO Fei, LI Jinzhong, ZHANG Shuqi. Comprehensive description of new-type transformer on-load tap-changer [J]. Electrotechnics Electric, 2013(10): 1-5.

[5] 梁贵书, 晏阔, 高飞, 等. 变压器混合式有载分接开关熄弧方法的仿真及试验研究 [J]. 高电压技术, 2014, 40(10): 3156-3163.

LIANG Guishu, YAN Kuo, GAO Fei, et al. Study on simulation and experiments of method of extinction hybrid on-load tap changer in transformers [J]. High Voltage Engineering, 2014, 40(10): 3156-3163.

[6] 张小宝. MR M型有载分接开关连续调档故障分析与处理 [J]. 冶金动力, 2020(5): 6-9, 17.

ZHANG Xiaobao. Fault analysis and treatment of continuous shifting adjustment of MR M-type on-load tap changer [J]. Metallurgical Power, 2020(5): 6-9, 17.

[7] 陆琳. 变压器有载分接开关电动机构故障分析及处理方法 [J]. 电工技术, 2018(5): 94-96, 98.

LU Lin. Fault analysis and treatment of motor-driving mechanism of on-load tap-changer in transformer [J]. Electric Engineering, 2018(5): 94-96, 98.

[8] 张德明. 变压器有载分接开关 [M]. 沈阳: 辽宁科学技术出版社, 1998: 126-130.

[9] 张姗, 张建辉, 郭晋伟. 新型智能有载分接开关控制器的设计 [J]. 通信电源技术, 2019, 36(3): 173-174.

ZHANG Shan, ZHANG Jianhui, GUO Jinwei. Design of new intelligent on-load tap switch controller [J]. Telecom Power Technology, 2019, 36(3): 173-174.

[10]徐磊, 朱孝勇, 张超, 等. 直线旋转永磁电机及其控制技术综述与新发展 [J]. 中国电机工程学报, 2020, 40(6): 1972-1984.

XU Lei, ZHU Xiaoyong, ZHANG Chao, et al. Overview and new development of linear and rotary permanent magnet machines and control technologies [J]. Proceedings of the CSEE, 2020, 40(6): 1972-1984.

[11]HAN Jingqing. From PID to active disturbance rejection control [J]. IEEE Transactions on Industrial Electronics, 2009, 56(3): 900-906.

[12]俞滨, 巴凯先, 刘雅梁, 等. 基于扩张观测器的液压驱动单元位置抗扰控制 [J]. 液压与气动, 2018(1): 1-8.

YU Bin, BA Kaixian, LIU Yaliang, et al. Research of anti-interference control method of hydraulic driving unit position control system based on external state observer [J]. Chinese Hydraulics & Pneumatics, 2018(1): 1-8.

[13]CHENG Haiyan, LI Dahai, ZHANG Jinhua, et al. Nonlinear error feedback positioning control for a pneumatic soft bionic fin via an extended state observer [J]. IEEE Access, 2020, 8: 12688-12696.

[14]CHENG Haiyan, ZHANG Jinhua, LI Yuanjie, et al. Finite-time tracking control for a variable stiffness pneumatic soft bionic caudal fin [J]. Mechanical Systems and Signal Processing, 2021, 152: 107314.

[15]DU Bochao, WU Shaopeng, HAN Shouliang, et al. Application of linear active disturbance rejection controller for sensorless control of internal permanent-magnet synchronous motor [J]. IEEE Transactions on Industrial Electronics, 2016, 63(5): 3019-3027.

[16]张德明. 分接开关技术的发展特点 [J]. 上海电器技术, 2005(3): 12-16.ZHANG Deming. The technology of tap changer develop characteristic [J]. Shanghai Electric Appliance Technology, 2005(3): 12-16.

[17]张德明. 真空分接开关技术的论述(7) [J]. 变压器, 2012, 49(2): 52-56.

ZHANG Deming. Discussion on the technology of vacuum tap changer(7) [J]. Transformer, 2012, 49(2): 52-56.

[18]上海华明电力设备制造有限公司. 数控分接开关电动机构: 中国, CN201320300019.9 [P]. 2013-11-06.

[19]上海华明电力设备制造有限公司. SHM-D分接开关数控操作机构使用说明书 [EB/OL]. (2021-08-26)[2021-10-01]. http:∥www.huaming.com/uploads/20210826/03bb6e29e3f4138057c0da2a7e8380f1.pdf.

[20]MARINO R, PERESADA S, TOMEI P. Nonlinear adaptive control of permanent magnet step motors [J]. Automatica, 1995, 31(11): 1595-1604.

[21]FLIESS M, LÉVINE L, MARTIN P, et al. Flatness and defect of non-linear systems: introductory theory and examples [J]. International Journal of Control, 1995, 61(6): 1327-1361.

[22]DEFOORT M, NOLLET F, FLOQUET T, et al. A third-order sliding-mode controller for a stepper motor [J]. IEEE Transactions on Industrial Electronics, 2009, 56(9): 3337-3346.

[23]韩京清. 自抗扰控制技术: 估计补偿不确定因素的控制技术 [M]. 北京: 国防工业出版社, 2008: 183-197.

[24]GAO Zhiqiang. Scaling and bandwidth-parameterization based controller tuning [C]∥Proceedings of the 2003 American Control Conference, 2003. Piscataway, NJ, USA: IEEE, 2003: 4989-4996.

[25]刘春强, 骆光照, 涂文聪, 等. 基于自抗扰控制的双环伺服系统 [J]. 中国电机工程学报, 2017, 37(23): 7032-7039.

LIU Chunqiang, LUO Guangzhao, TU Wencong, et al. Servo systems with double closed-loops based on active disturbance rejection controllers [J]. Proceedings of the CSEE, 2017, 37(23): 7032-7039.

[26]BODSON M, CHIASSON J N, NOVOTNAK R T, et al. High-performance nonlinear feedback control of a permanent magnet stepper motor [J]. IEEE Transactions on Control Systems Technology, 1993, 1(1): 5-14.