基于多元回归分析陕西省物流业发展的环境影响

黄钰茜

摘要：物流活动的运输、配送等环节会释放出有害气体造成大气污染和形成交通堵塞、带来噪声污染等，给环境带来许多不良影响。文章将陕西省物流业作为研究对象，采用多元回归分析2009～2018年物流业带来的环境影响，以期为陕西省物流业的发展提供一定参考。以交通运输、仓储、邮政业增加值作为因变量，陕西省主要城市道路交通噪声平均等效升级、陕西省生活垃圾清运量、陕西省油品消耗量、陕西省工业废气排放量作为自变量进行分析。结果表明交通运输、仓储、邮政业增加值对工业废气排放量的影响大于生活垃圾清运量的影响。

关键词：陕西省;物流业;环境;多元回归;SPSS

一、引言

陕西省作为西北地区门户，具备天然的地理优势。同时，陕西省正处在从工业化中期向后期跨越的关键时期，深度融入共建“一带一路”，新时代推进西部大开发形成新格局、黄河流域生态保护和高质量发展等国家重大战略深入实施的多重机遇不断影响着陕西省物流业的发展趋势。然而，研究表明，物流业是高耗能产业，在快速发展的同时也成为我国碳排放增长速度最快的行业之一，并带来了空气污染、噪声污染、粉尘污染等不良环境影响。王晓华通过模型对比，选择LEAP模型和情景分析法对北京市物流发展对节能减排的影响进行研究。丁长峰利用Dea-malmqusit指数方法测定中部六省2000～2011年间物流产业生产效率，并采用Tobit模型分析环境影响因素。谢阿红等采用多元回归模型对影响华东六省一市绿色物流绩效排名的原因进行深入分析，并给出提高绿色物流发展水平的建议。上官绪明采用非限制性VAR模型为基础研究我国1990～2010年碳排放量与物流业之间的动态演进关系，结果表明物流业的快速发展导致能源消耗的增长和碳排放量的上升。绿色经济的发展离不开现代物流业的支撑，研究物流活动对环境造成的影响具有较大的现实意义与实用价值。故本文采用多元回归来对陕西省物流业发展的环境影响进行分析。

二、模型简介

用于分析物流环境影响的方法有很多，比如线性回归法、指数平滑法、弹性系数法和灰色预测法等。不同方法具有不同的特点和适用情况，具体如表1所示。

多元线性回归分析是在线性相关的情况下，分析两个或两个以上的自变量和一个因变量之间的数量变化关系。注重分析不同变量的数值发展规律，并运用一定的数学关系式描述所分析的结果，从而得到自变量的变化对因变量的影响水平的表达式。

多元线性回归模型可以表示为以下表达式：

Y=β0+β1X1+β2X2+βkXk+ε

其中，β0，β1X1，β2X2，…βkXk代表k+1个不解的参数;β0称为回归常数，β1，β2，βk称为回归系数;Y称为因变量;X1，X2，…Xk表示可以控制的变量，称为自变量;

ε表示误差项的随机误差，它是无法由X与Y之间的线性关系所解释的变异性，反映的是其他随机因素对因变量的影响。

（一）判断相关关系

若几个变量之间不存在任何关系，就无法建立模型或回归分析。

（二）模型的整体检验

对多元回归方程进行的整体性检验，就是研究各个自变量是否从整体上对因变量有明显的影响，需用到F统计量，来检验分析两者之间的差别是不是显著。如果具有明显的影响，就说明二者存在线性关系;反之，则不存在。对多元回归模型进行整体性检验过程如下：

1.提出假设。

H0：β1=β2=…=βk

H1：至少有一个回归系数不等于0。

若无法拒绝原假设，则表示回归模型不能明显地预测因变量，若可以拒绝原假设则表示有自变量可以显著地预测因变量。

2.计算检验统计量F。F检验一般是分析不止一个参数的统计模型，从而判断模型的所有或一些参数是不是可以估计模型。

3.确定显著性水平a和分子自由度m、分母自由度n-m-1，找出临界值Fa

4.作出决策：若F>Fa，拒绝H0;若F≤Fa，接受H0

（三）回归系数的显著性检验及共线性检验

在多元线性回归中，对每一个自变量都要分别进行检验，应用t检验。步骤如下：

1.提出假设。

H0：βk=0（自变量X与因变量Y没有线性关系）

H1：βk≠0（自变量X与因变量Y有线性关系）

2.计算检验的统计量t。

3.确定显著性水平a，并作出决策。

|t|>ta/2，拒绝H0，|t|≤ta/2，不拒绝H0。

三、实例分析

（一）数据收集

就目前的物流业来看，众多物流环节都离不开交通运输，交通运输是物流行业中比较重要的环节，在物流的总成本中占到50%以上。故本文采取交通运输、仓储、邮政业增加值来代表物流业的变化值，并采用回归分析对物流相关问题进行分析。

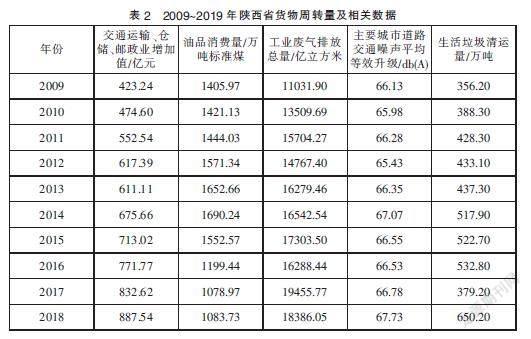
由于部分指标数据未更新至最新年份，受统计数据可获得性限制，故本文选取陕西省2009～2018年的交通运输、仓储、邮政业增加值（亿元）作为因变量Y。由于物流的发展会带来废气污染、噪声污染、运输车辆燃油污染等环境污染，故自变量分别为：陕西省主要城市道路交通噪声平均等效升级（db（A））、陕西省生活垃圾清运量（万吨）、陕西省油品消耗量（万吨标准煤）、陕西省工业废气排放量（亿立方米），分别令为自变量X1、X2、X3、X4。通过建立多元线性回归模型，探究并分析各自变量与因变量之间的干系，并采用SPSS.21軟件对所含数据处理分析。从近十年的《中国统计年鉴》和《陕西统计年鉴》获得所需数据如表2所示。

（二）数据分析412CECCE-A96B-4904-87B8-97B27D9D24E6

1. 相关关系判断。一般而言，变量之间要么存在函数关系，要么存在相关关系。本文主要采用回归分析的方法来研究因变量与自变量之间存在的相关关系。运用SPSS.21软件得出交通运输、仓储、邮政业增加值与各自变量之间的矩阵散点图。（见图1）

从图1可以明显看出因变量与各自变量之间存在相关关系。

2. 多重样本决定系数。因本文是分析各自变量对因变量的影响程度，所以在SPSS中采用强行进入法，最终得到模型，其回归分析输出结果和其数据如表3～表7所示。

表4中R为相关系数，R方为相关系数的平方，也被叫作判定系数（多重样本决定系数），用以反映回归直线的拟合程度，R方的取值范围在[0，1]内，R方愈向1接近，就表示回歸方程拟合得愈好;R方愈向0接近，就表示回归方程拟合得愈不好。通常而言，大于0.800意味着回归方程对样本数据的吻合水平高。由表4可以发现，Y与X的相关系数为0.973，判定系数为0.947，调整后的判定系数为0.904。以上结果可以说明各自变量能较好地解释因变量，差不多解释90.4%的因变量的变化。

3. 模型的整体检验。表5给出了回归方程的方差分析及检验结果，F代表构造的统计量的值，Sig.代表显著性水平。模型中Sig.一般同显著性水平0.05进行比较，表5中的F值相对的Sig.值是0.002，显然小于0.05水平，统计上非常显著，说明线性模型能够使用。

Sig结果表示T统计量所映射的概率值，并规定Sig值要小于已定的显著性水平，且越向0靠近越好。F是平均的回归平方和与平均剩余平方和之比，它的结果数值越高，说明结果越优秀。显著性水平为0.1时，df=（4，5），查表得Fa的临界值为4.051。所以F>Fa，落入拒绝域，表示至少有一个自变量可以增加预测因变量显著性。

4. 回归系数的显著性检验及共线性检验。SPSS分析出了多元线性回归计算模型的系数表，其中B表示回归模型的偏回归系数、t表示检验的统计量，Sig.代表显著性水平，VIF代表方差膨胀因子，用来解释自变量间存在的多重共线性。取显著性水平为0.1，对各个自变量进行检验，查表得临界值ta/2=2.0150。所以|t|>ta/2，由表6可知，生活垃圾清运量、油品消耗量、工业废气排放量与因变量具有线性关系。

相关研究数据显示，0≦VIF<10时，多重共线性几乎不存在;10≦VIF<100时，说明有较强多重共线性;VIF≧100时，表示多重共线性非常显著，表6中VIF值在1～3左右，表明各变量之间没有多重共线性关系。

结合实际可知，交通运输、仓储、邮政业增加值与物流货运量成正相关，而货运量与运输车辆及其产生的道路交通噪声和油品消耗量也成正相关。根据模型分析结果，将剔除自变量中的道路交通噪声和油品消耗量，最后得到的回归模型如下：

Y=1743.947+0.5942X2+0.43X4

从上述回归方程结果可以看出，生活垃圾清运量每增加1万吨，交通运输、仓储、邮政业增加值就增加0.594亿元;工业废气排放量每增加1亿立方米，交通运输、仓储、邮政业增加值就增加0.43亿元。生活垃圾清运量中的30%由物流活动产生，生活垃圾清运量的回归系数为0.594，大于工业废气排放量的回归系数0.43。同样的，可以说明交通运输、仓储、邮政业增加值对工业废气排放量的影响更大一些，同时，对生活垃圾清运量的影响也不容小觑。

四、结语

通过分析陕西省物流业对环境产生的影响结果得知，交通运输、仓储、邮政业增加值越大，带来的环境影响就越大。并且对工业废气排放量的影响稍大于对生活垃圾的影响。对此，本文给出如下建议：一方面，大力发挥政府的监督引导作用，加大对绿色物流的扶持力度，制定并出台相关政策;另一方面，大厂应担当社会责任并起到带头示范的作用;同时，加大对高校相关研究方向的人才培养。

参考文献：

[1]王晓华.基于LEAP模型的北京市物流发展对节能减排影响研究[D].北京：北京交通大学，2009.

[2]丁长峰.中部地区物流产业生产效率及其环境影响因素分析[J].生产力研究，2013（04）：106-108+201.

[3]谢阿红，薛倩玉，周泽炯.区域绿色物流绩效评价及影响因素的研究——基于“华东六省一市”的数据[J].九江学院学报（自然科学版），2019，34（02）：44-50.

[4]上官绪明.我国物流业对环境影响的动态效应研究——基于非限制性VAR模型的经验[J].生态经济，2013（08）：111-114+143.

[5]李隽波，孙丽娜.基于多元线性回归分析的冷链物流需求预测[J].安徽农业科学，2011，39（11）：6519-6520+6523.

[6]李金林，赵中秋，马宝龙.管理统计学[M].北京：清华大学出版社，2016：224-229.

[7]曹银华，巫文杰，李澳.“一带一路”倡议下广东省国际贸易与国际物流协同发展研究[J].中国商论，2021（01）：124-127.

[8]张鑫.物流产业集聚的工业减排效应——基于长三角空间面板模型[J].价值工程，2019，38（19）：92-95.

[9]武进静，韩兴勇.基于多元线性回归模型对江苏省物流需求的预测分析[J].上海农业学报，2015，31（04）：62-68.

（作者单位：西安财经大学管理学院）412CECCE-A96B-4904-87B8-97B27D9D24E6