考虑风险管理的电力市场多时段均衡分析方法

唐成鹏，张粒子，邓 晖，肖艳炜

（1. 华北电力大学电气与电子工程学院,北京市 102206；2. 国网浙江省电力有限公司电力科学研究院,浙江省杭州市 310014；3. 国网浙江省电力有限公司电力市场仿真实验室,浙江省杭州市 310014；4. 国网浙江省电力有限公司,浙江省杭州市 310000）

0 引言

电力市场均衡分析在市场运行模拟及机制设计［1］、市场主体交易决策及市场力分析［2］、电价预测及源网荷投资规划［3］等众多方面都起着至关重要的作用。双层优化模型是目前主流的电力市场均衡建模方法［4-7］,其求解方法主要有2 类:一类是模型转化法,即通过KKT（Karush-Kuhn-Tucker）最优化条件或强对偶定理［8］将双层模型转化为单层的带均衡约束的数学规划模型（mathematical programming with equilibrium constraint,MPEC）［9］或带均衡约束的均衡优化模型（equilibrium problem with equilibrium constraint,EPEC）［6］进 行 求 解；另 一 类 是 迭 代 求 解法,通常采用基于智能体模型（agent-based model）的优化算法,如强化学习［10-12］和深度强化学习［13-15］等。由于模型转化需满足下层模型为凸优化问题的前提条件,因此,不适用于电力市场中的机组组合出清模型［16］,常用于解决单时段的市场均衡问题。多时段的市场均衡问题可采用迭代求解法,其中深度强化学习方法避免了强化学习对动作空间进行离散化而可能导致的“维数灾”问题,并有助于对大规模系统模型的求解［17］。

然而,当前的电力市场多时段均衡分析方法主要聚焦于风险中立型市场主体参与电能量或辅助服务市场的情形,暂未考虑实际市场主体的风险偏好差异,以及其在差价合同和现货交易中进行风险管理的影响,从而限制了均衡分析方法的实用性。解决上述考虑风险管理的电力市场多时段均衡问题将面临3 个方面的挑战:一是差价合同包括市场化差价合同和政府授权差价合同［18］,这2 类差价合同的建模方式以及对市场运行的影响各不相同,并且在关注多时段的均衡问题时,差价合同曲线的确定方式也将成为一个关键难点；二是随着风险特征的引入,模型将会由确定性向随机性转变,大大增加了模型构建的复杂性［19］；三是对求解方法提出了较高要求,如何确保市场主体能在不确定环境中具备鲁棒的决策能力、求解得到稳定的市场均衡结果是解决该问题的关键。

鉴于此,本文分别设计了市场化差价合同和政府授权差价合同的确定方式,并采用条件风险价值（conditional value at risk,CVaR）［20］评估市场风险,构建计及差价合同和风险偏好的电力市场均衡模型；在深度强化学习基础上,提出了风险管理的多智能体深度强化学习算法,实现了对风险敏感型随机优化模型的高效求解。

1 市场均衡模型

1.1 模型框架

计及差价合同和风险偏好的电力市场多时段均衡模型包括差价合同的确定、发电商报价决策模型和现货市场出清模型3 个部分,如图1 所示。

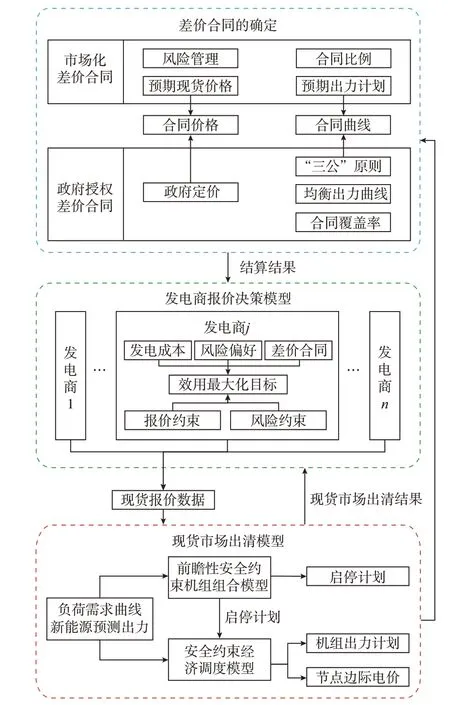
图1 电力市场均衡模型框架图Fig.1 Framework diagram of equilibrium model for electricity market

第1 部分分别考虑了市场化和政府授权2 类差价合同。对于前者,此阶段模拟市场主体签订差价合同,假设各发电商根据预期的发电出力和现货价格签订合同,将预期出力曲线按某一合同比例Z（0%≤Z≤100%）折算得到各自的差价合同曲线,合同价格由预期现货价格及发电商风险管理倾向共同决定；对于后者,基于“三公”原则确定各机组的合同总量,并根据无差价合同时现货市场均衡出力曲线形状及某一合同覆盖率F（0%≤F≤100%）在事前确定差价合同曲线。第2 部分考虑了各发电商的风险偏好特征,在规则允许范围内,各发电商以效用最大化为目标进行现货市场的报价决策。第3 部分以日为周期进行现货市场出清,采用前瞻性安全约束机组组合模型决定机组启停计划,机组发电功率的经济分配和节点边际电价由安全约束经济调度模型确定。

在该模型框架中,市场化差价合同部分的预期出力曲线及现货价格由现货市场出清结果确定；政府授权差价合同的价格及曲线均在现货市场前确定；各发电商基于差价合同、自身成本及风险偏好等信息优化其报价策略；现货市场综合所有报价信息进行多个新能源预测出力或负荷需求场景的出清计算,并将出清结果反馈给各发电商,确定其在现货市场和合同市场的结算收益,以此作为发电商优化决策的依据。以此循环,直至达到纳什均衡。

其他假设描述如下:

1）合同结算点默认为机组所在节点,实际中可通过购售双方协商或借助金融输电权实现。

2）文献［21］论证了实现确定的现货市场均衡状态的前提是报价曲线的斜率和截距只能有一个是独立决策变量；文献［22］在理论上证明了差价合同主要影响报价曲线截距。鉴于此,本文以截距倍率ki（0≤ki≤Kmax）作为机组i在现货市场中报价的决策变量,报价曲线由ki与边际成本曲线截距的乘积,以及边际成本曲线斜率共同形成,其中Kmax为报价决策变量的上限值。ki=1 表示机组i按照实际的边际成本报价；ki＞1 或ki＜1 表示机组i按照高于或低于实际的边际成本报价。

1.2 市场化差价合同的确定

不失一般性,本文以期望出力曲线与合同比例的乘积结果作为机组签订的最终差价合同曲线,即:

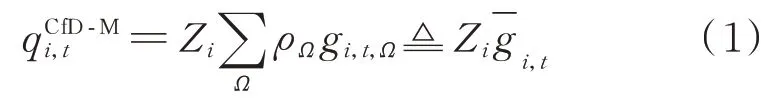
对于合同价格,根据“现货-期货平价定理”［23］,当市场流动性充裕、购售主体均为理性且风险中立时,合同价格将趋近于现货市场价格期望值。考虑到实际电力差价合同市场的流动性相对不足,并且市场主体风险偏好会对其签订的合同价格造成影响,本文以与合同覆盖范围内现货市场价格期望值的偏差表示合同价格,即

1.3 政府授权差价合同的确定

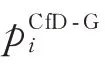
鉴于此,本文在不考虑差价合同（F=0）的电力现货市场均衡结果基础上,首先按照装机容量比例分配确定各机组的最大合同电量（F=1）,并考虑各机组的合同覆盖率F要求进行折算,确定其合同电量；继而,根据均衡结果中对应机组的出力曲线形状进行电量分解,确定政府授权合同曲线,表示如下:

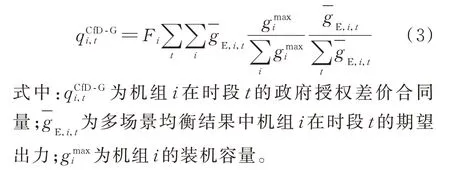
1.4 发电商报价决策模型

发电商可拥有多台机组,对于任一发电商j,其通过优化现货市场的报价策略,力求实现总利润最大化和风险最小化的目标。以CVaR 衡量发电商的低利润风险,建立各发电商报价决策的随机优化模型。

1）目标函数

式（5）是发电商j效用最大化目标函数,包含利润期望和风险效用两部分。利润期望由所属各机组的差价合同收益、现货市场收益和发电总成本组成,其中现货市场中各机组发电量按所在节点电价进行结算；风险效用部分由风险偏好和在α置信度水平下的CVaR 值组成。

对于市场化差价合同,结合式（1）和式（2）,式（6）可写为:

合同市场总期望收益可化简为:

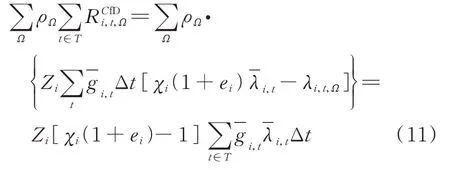
目标函数式（5）可整理为:

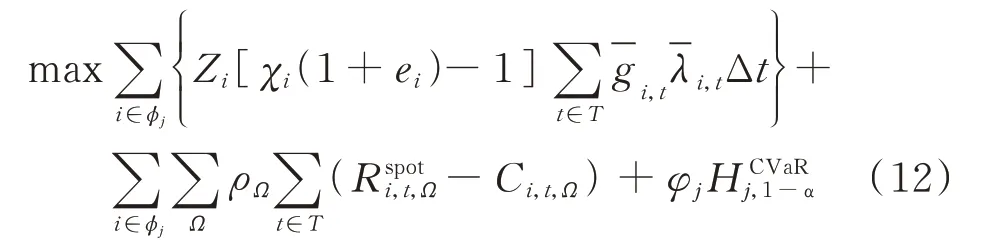
通过式（12）可以看到,在市场流动性充裕（χi=1）的理想情况下,当发电商j属于风险中立（φj=0,ei=0,i∈φj）时,其差价合同的期望收益为0,总利润不受差价合同影响；当发电商j属于风险厌恶（φj＞0,ei＜0,i∈φj）时,差价合同的期望收益为负,并且随着其风险厌恶程度和合同比例增大,总期望利润也会变小。总之,差价合同在减少发电商期望收益（付出风险贴水）的同时,也提高了可能的最小收益（减少了可能的最大损失）,对发电商而言,起到了风险对冲的作用。

对于政府授权差价合同,式（6）可整理为:

目标函数式（5）为:

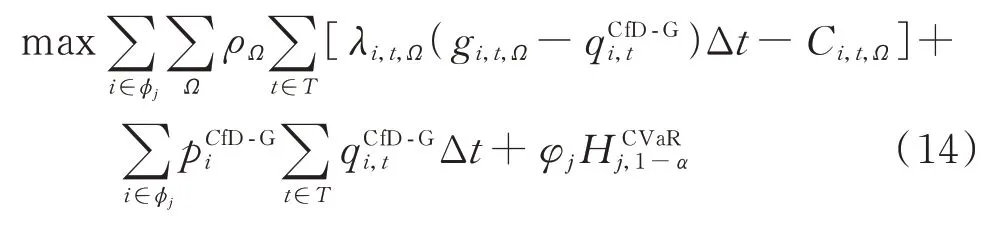
2）约束条件

1.5 现货市场出清模型

现货市场以新能源预测出力作为边界条件。为保证出清结果的最优性和合理性,避免出现末时段大量机组停机的不合理结果,采用前瞻性安全约束机组组合和经济调度的组合模型构成下层现货市场出清模型。

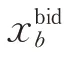
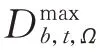
前瞻性安全约束机组组合模型的目标函数为:

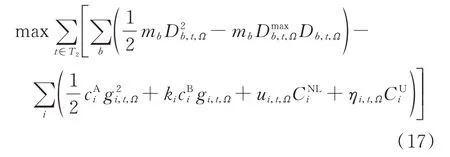
式 中:ηi,t,Ω为 启 机 状 态 转 换 变 量,当 且 仅 当ui,t,Ω=1且ui,t-1,Ω=0 时,ηi,t,Ω=1,否则,ηi,t,Ω=0；T2为考虑前瞻性的总时段集合。

约束条件包括系统功率平衡约束、系统备用约束、负荷需求约束、发电机组运行特性约束、网络潮流约束等（见附录A）。

在整个模型框架中,发电商报价决策模型的变量ki（i∈φj）决定了现货市场的报价信息,市场优化出清得到的ui,t,Ω、gi,t,Ω、λi,t,Ω等结果反馈给各发电商,以确定其差价合同和现货市场的总收益。通过不断交互迭代,最终实现均衡。

2 基于风险管理多智能体深度强化学习的模型求解

整个模型框架可基于风险管理的多智能体深度强化学习方法进行迭代求解。本文在多智能体深度确定性策略梯度（multi-agent deep deterministic policy gradient,MADDPG）［26］算 法 基 础 上,通 过 改进提出了风险管理的多智能体深度确定性策略梯度（risk-managing MADDPG,RM-MADDPG）算法。其中,现货市场出清模型属于混合整数二次规划问题,可借助商用求解器Gurobi 进行优化计算。

2.1 深度强化学习要素设置

RM-MADDPG 基于马尔可夫决策过程建立,以各发电商作为有自主学习能力的智能体（agent）,而将与之交互的合同市场和现货市场作为环境。其要素包括:

1）状态s:以各机组的差价合同比例（或覆盖率）、上一轮交互各机组加权平均电价的期望值λ1,d-1,λ2,d-1,…,λI,d-1, 作 为 状 态sd={Z1,Z2,…,ZI,λ1,d-1,λ2,d-1,…,λI,d-1}（或sd={F1,F2,…,FI,λ1,d-1,λ2,d-1,…,λI,d-1}）∈S,其中,I为参与市场竞争的机组总数；S为状态集合；下标d为强化学习的交互次数。

2）动作a:智能体j的动作是所属机组报价决策变量kj的集合,kj∈A=［0,Kmax］,所有机组的联合动作集合表示为O={a1,a2,…,aI}；A为动作空间的集合。

3）策略μθ:以状态和动作间的映射关系表示μθ:S→A,θ为参数,根据状态s获得确定的动作,即a～μθ（s）。

5）智能体的状态转移由市场出清过程决定；状态-动作值函 数Q(s,a)=Ea～μθ{rtot,j|(s,a)},定 义为在状态s下选择动作a并随后采用策略μθ所得到的累积回报的期望值；E{·}为期望函数。

在MADDPG 基础上,本文所提RM-MADDPG算法主要从3 个方面进行改进:一是与随机优化模型相契合,修改了原算法中经验储存及采样的信息集,以适应从单一场景到多场景的拓展；二是增加了风险参数估计模块,将风险值和智能体偏好反映到策略网络和值网络的更新学习之中,以实现发电商报价决策的优化目标；三是结合风险约束强化学习（risk-constrained RL）的理论研究成果［27］,明确了策略网络和值网络学习速率的配合关系,以保证算法的收敛性。

2.2 RM-MADDPG 框架

RM-MADDPG 框架如图2 所示。各智能体主要由策略网络（Actor）、Q 网络（Critic）和风险参数估计3 个部分构成。策略网络包括参数为θ的主策略网络（actor online network,AON）和参数为θ′的目标策略网络（actor target network,ATN）；Q 网络包括 参 数 为ω的 主Q 网 络（critic online network,CON）和 参 数 为ω′的 目 标Q 网 络（critic target network,CTN）。其中,策略网络的功能是根据状态s和确定性策略μθ选择动作a,与环境进行交互；Q网络的作用是对策略网络的行为进行评价,并指导其后续动作；风险参数估计部分是通过对风险参数δj,Ω和νj的估计,评估相应动作可能面临的风险,使智能体的决策计及风险因素的影响。主网络（AON、CON）采用梯度方式进行训练和更新,目标网络（ATN、CTN）定期从主网络复制参数,并采用软更新方式进行训练。策略网络各层的神经元分别以修正线性单元（rectified linear unit,ReLU）和双曲正切函数（tanh）作为激活函数；Q 网络各层的神经元分别以ReLU 和线性函数（linear）作为激活函数。整个框架采用集中训练和分散执行方式进行,详细过程见附录B。

图2 RM-MADDPG 框架图Fig.2 Framework diagram of RM-MADDPG

式中:ε为衰减率,通常为极小的正数；MB为储存器Bj储存的总次数；Mtrain为训练总次数。

2）风险参数估计

通常情况下,CVaR 难以直接计算。为满足式（15）中的风险约束,可基于样本数据对CVaR 进行估计:

式中:νj,1-α取rj,d,Ω序列的1-α分位数；rj,n,Ω为场景Ω下智能体j的第n个样本的回报。

3）主Q 网络训练

主Q 网络的训练目标是最小化样本Q值和目标Q值之间的均方差,其误差函数L(ωj)为:

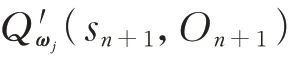
根据自动微分技术［28］可计算其梯度,ωj按下式更新:

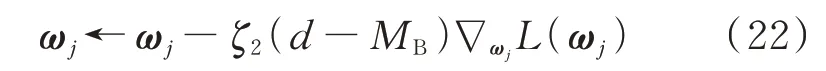
式中:ζ2为主Q 网络的学习速率。

4）主策略网络训练

确定性策略J(μθj)梯度公式为:

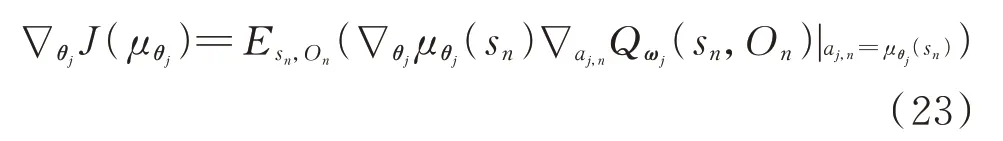
根据蒙特卡洛方法,将采样数据集代入式（23）,可以作为对该期望的一个无偏估计值,将该式改写为采样策略梯度:

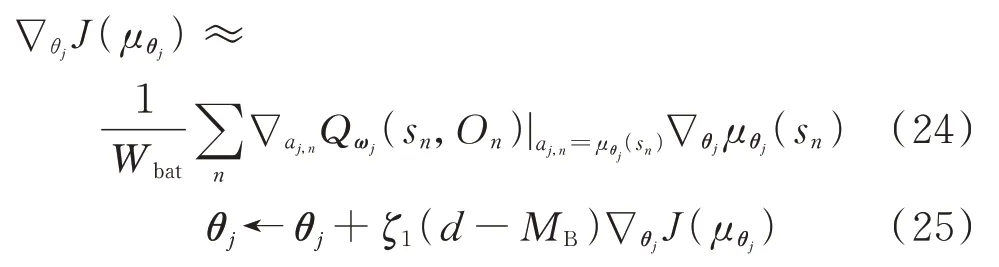
式中:ζ1为主策略网络的学习速率。

5）更新目标网络参数

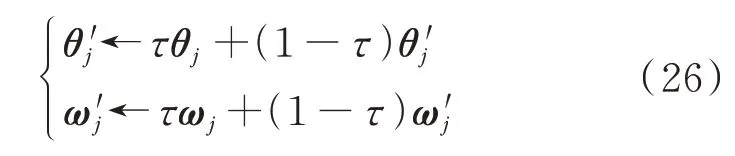
式中:τ 为目标网络的学习速率。

为保证算法的收敛性,主网络学习速率ζ1和ζ2应满足以下约束:

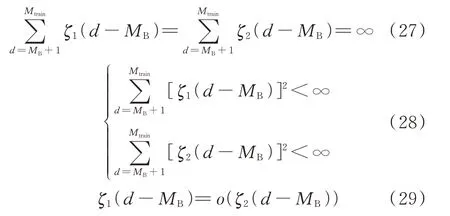
式中:o(·)表示高阶无穷小。

整个算法基于PyTorch 和Gurobi 框架进行编程和计算。

3 算例分析

3.1 算例基础及参数设置

本文采用文献［29］的算例数据,共包含30 个节点、41 条线路、6 台火电机组和20 个负荷,并在节点29 处增加1 个新能源场站。火电机组的其他运行参数及节点负荷分布因子分别见附录C 表C1 和表C2。通过3 个负荷需求场景和3 个新能源典型出力场景组合形成9 个净负荷场景（见附录C 图C1）,各负荷场景下负荷需求曲线的斜率按照该场景与中负荷场景的负荷比例缩放形成。算例考虑相同合同覆盖率（合同比例）情况,此时状态空间可缩减为7 维。

神经网络由输入层、2 个隐藏层和输出层构成,策略网络各层的神经元个数分别设置为7、128、64和发电商所拥有的机组数,分别以ReLU 和tanh 函数作为2 个隐藏层和输出层的激活函数；Q 网络各层的神经元个数分别设置为状态s和动作集O的总维数13、128、64、1,分别以ReLU 和linear 函数作为2 个隐藏层和输出层的激活函数。由于tanh 函数输出值a′的取值范围为［-1,1］,因此,需按a=（a′+1）Kmax/2 缩放到合适的报价动作区间［0,Kmax］。主网络采用Adam 优化器［30］进行训练。其他参数为ζ1=0.001（d-MB）-0.36,ζ2=0.001（d-MB）-0.34,Δt=1 h,Kmax=3,α=0.95,ε=0.001,τ=0.01,γ=0,MB=1 000,Mmax=6 500,Mtrain=6 200,Wbat=80。

下面重点分析合同市场流动性充裕（χi=1）、每个发电商拥有1 台机组的理想情况。在此基础上,附录D 给出发电商拥有多台机组、合同市场流动性不足等案例,进一步探讨其对结果的影响。

3.2 考虑风险偏好的电力现货市场均衡结果分析

在不计及差价合同时,设置表1 中4 种不同风险偏好特征的案例,其中Ⅰ和Ⅱ分别是风险爱好型和风险中立型案例,Ⅲ和Ⅳ为风险厌恶型案例。

表1 不同风险偏好特征案例信息Table 1 Case information of different risk-preference features

通过各案例下的电力现货市场均衡结果（见图3）可以看到,风险爱好型发电商倾向于抬高报价,在承担一定风险的同时追求可能的更高收益；而随着风险厌恶程度增加,发电商报价逐步降低,但并不低于实际边际成本。特别地,G5 机组由于具备位置优势,大多数情况下其节点价格由其他机组决定,且高于发电侧平均电价,该机组常采用价格接受者的策略,通过最大化中标电量的方式提高利润。而在案例Ⅲ中G5 机组风险厌恶程度较高的情况下,为避免极端情况下可能的亏损情况,其报价策略转变为采用接近于实际边际成本的报价。

图3 各案例k 值对比结果Fig.3 Comparison results of k values in each case

附录C 图C2 展示了各案例下机组的利润水平和风险情况,案例Ⅰ各场景的市场出清结果见附录C 图C3。可以看到,部分机组有能力通过调整自身报价策略并影响其他机组报价决策,进而在一定程度上改变市场均衡结果。以案例Ⅱ和Ⅲ为例,随着G5、G6 机组风险厌恶程度的增加,其通过调整报价策略明显抬高了CVaR 值,实现了风险规避。

3.3 计及市场化差价合同和风险偏好的市场均衡结果分析

本节重点分析表1 中Ⅰ至Ⅲ这3 个案例,其中e取对应φ值的-5%。图4 展示了不同比例市场化差价合同下各案例的均衡情况。可以看到,差价合同比例及发电商的风险偏好特征会作用于自身报价决策,进而影响其他发电商的报价策略,最终达到新的市场均衡状态。

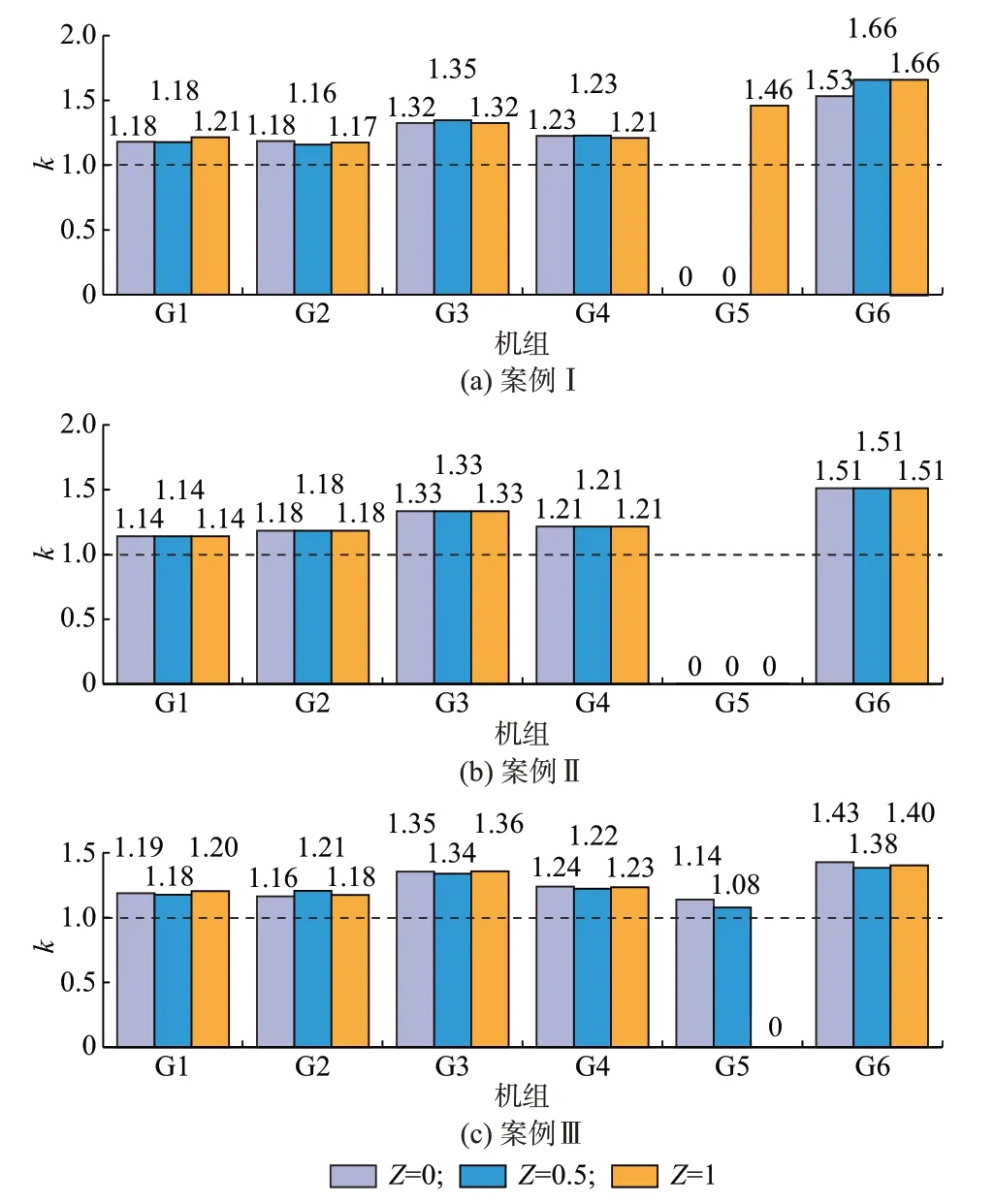
图4 不同合同比例下k 值对比结果Fig.4 Comparison results of k values with different contract ratios

1）不考虑风险偏好时（案例Ⅱ）,发电商报价决策不受市场化差价合同影响。因为当发电商为风险中立时,合同价格接近于现货价格期望值,不同比例差价合同并不会对发电商的期望利润造成影响。

2）相同比例合同情况下,随着发电商风险厌恶程度逐步提高,其报价呈降低趋势。

3）随着合同比例增大,风险爱好型发电商倾向于抬高报价,均衡结果中机组期望利润也随之增加；风险厌恶型发电商会略微降低报价,均衡结果中机组期望利润也随之降低。

4）当合同比例Z=1 时,市场均衡状态并非完全竞争水平。这是因为合同价格与现货市场价格联动,若发电商接近于边际成本报价（k=1）,则将使差价合同及现货市场的结算收益减少,与效用最大化的目标背道而驰。

3.4 计及政府授权差价合同和风险偏好的市场均衡结果分析

基于均衡结果确定的政府授权差价合同曲线如附录C 图C4 所示,合同价格设定为38 元/（MW·h）。在此边界下,不同合同覆盖率的均衡情况如图5所示。

图5 不同合同覆盖率下k 值对比结果Fig.5 Comparison results of k values with different contract coverage ratios

可以看到,2 类差价合同对发电商报价的影响有一定相似性,而政府授权差价合同对市场均衡的影响更为明显,主要体现在以下3 个方面:

1）无论是风险偏好变化的机组G5 和G6,还是风险偏好不变的G1 至G4,其报价均随合同覆盖率的增加而降低。相较于考虑市场化差价合同的结果,政府授权差价合同下机组报价随合同覆盖率变化的幅度更大。

2）政府授权差价合同会对风险中立型发电商（案例Ⅱ）的报价策略产生影响,随着合同覆盖率的增加,发电商报价明显降低。这与政府授权差价合同对风险厌恶型发电商的影响类似。

3）在F=1 时的合同覆盖率下,接近于边际成本报价（k=1,偏差取决于各机组差价合同总电量与实际总发电量的差异）是发电商实现效用最大化的最优策略。即表明,当合同覆盖率F=1 时,现货市场接近于完全竞争。

附录C 图C5 展示了不同合同价格情况下案例Ⅲ的市场报价变化趋势,明确了政府授权差价合同价格的设定并不会对市场均衡结果产生影响。

4 结语

本文针对实际电力市场中差价合同及市场主体风险偏好问题,完整提出了考虑风险管理的电力市场多时段均衡分析方法。优化结果表明,本文所提模型和方法可以有效计及市场主体在差价合同和现货市场中进行风险管理的影响,模拟多时段的电力市场均衡情况,为电力市场的机制设计和运行分析提供实用化的数值分析工具。相关结论和建议如下:

1）市场主体风险偏好和电力差价合同会对市场运营产生较大影响,市场设计需统筹考虑。

2）电力差价合同可以为市场主体提供有效的风险管理手段。市场化合同主要通过缩小各场景的利润偏差,控制市场风险可能给市场主体造成的损失来发挥风险管理作用,其产品设计应注重提高合同市场的流动性,如设置标准化产品和枢纽节点、优化交易机制、扩大主体范围等。

3）政府授权差价合同对市场均衡的影响显著,对市场主体行为的约束力较强,有利于中国现货市场稳妥起步。建议采用本文方法在事前确定合同曲线,尽量减少因事后合同电量分解不合理造成的公平性或市场低效问题。

4）设置合适的差价合同覆盖率（或合同比例）要求,无论对市场主体管理交易风险,还是对监管机构管控市场力、促进电力市场高效运营都有积极意义。

本文研究以新能源出力作为市场边界,暂未考虑新能源主动参与市场的影响。为适应未来以新能源为主体的新型电力系统,市场均衡分析方法还需完善对新能源参与市场的考虑,在此基础上探讨适用于新型电力系统的市场机制设计方法,这将是后续的研究重点。