部分充电策略下的多车型电动汽车车辆路径优化问题研究

程 坦，陈 鹏，张国伟，朱 宁

（1.天津大学，管理与经济学部，天津 300072；2.复旦大学，管理学院，上海 200433；3.广东美的制冷设备有限公司，佛山 528311）

0 引言

在新能源汽车购置补贴、路权便利等政策的引导下，诸多大型物流企业纷纷采用电动汽车替代传统燃油型物流车。然而，电动汽车在实际使用过程中却面临着行驶里程受限、充电困难等问题。因此，通过对电动汽车行驶路径、充电策略进行优化，以提高配送效率，降低配送成本，实现电动货运的进一步推广。

传统车辆路径规划问题主要研究燃油车路径优化，并在多场景得到应用，例如物流配送[1]、物流包装回收[2]、垃圾回收[3]等。然而随着电动汽车的普及与发展，电动汽车的车辆路径规划问题（Electrical Vehicle Routing Problem，EVRP）受到更多的关注。Schneider 等[4]提出可变邻域搜索算法与禁忌搜索算法相结合的混合启发式算法，引入有限车辆数和顾客时间窗两个约束，分析具有时间窗的电动汽车车辆路径优化问题。Desaulniers 等[5]研究了单一车型电动汽车4种不同充电策略，在考虑顾客时间窗约束条件下，设计精确算法对问题进行求解，结果表明部分充电策略可以降低配送总成本。Macrina 等[6]研究了混合车队中电动汽车充电策略问题，并考虑了行驶过程中加速、减速对能耗的影响，设计了大规模邻域搜索算法进行求解。Penna 等[7]考虑不同类型电动汽车，结合集合分割模型，提出一种迭代邻域搜索算法，求解具有时间窗的多车型电动汽车车辆路径优化问题。Montoya等[8]在考虑电池充电时间为非线性函数的条件下，设计一个混合启发式算法，并对比分析了线性充电函数和非线性充电函数的影响。杨珺等[9]采用两阶段启发式算法，考虑电动汽车物流配送网络的设施选址和配送路径优化问题。揭婉晨等[10]构建了包含时间窗的多车型电动汽车VRP 模型，运用分支定价算法进行最优化求解。何东东和李引珍[11]设计改进禁忌搜索算法，考虑油耗和碳排放量的问题，研究了带时间窗的EVRP问题。郭放等[12]采用启发式算法，考虑了差异化服务成本与充电策略问题，并建立出整数规划数学模型。杨森炎等[13]基于时空状态网络建立整数规划模型，并利用前项标号法进行求解。

综上所述，现有的电动汽车EVRP问题的研究已经取得了一定的进展，但是缺少对车型的考虑。然而城市道路交通网络日益复杂，多车型配送也愈发普遍，已有文献中的完全充电策略受充电时长和顾客时间窗限制，必须选择更多的车辆来满足任务需求，增加了配送总费用。本研究根据实际物流配送场景，引入多车型，采用部分充电策略，放松充电需要充满电的假设，考虑时间窗和资源约束，构建部分充电策略下的多车型车辆路径问题的混合整数规划模型，设计局部搜索算法增强的自适应大规模邻域搜索算法对模型进行求解，通过数值实验验证算法的有效性和策略的可行性。同时利用不同规模算例与完全充电策略进行对比，结果表明部分充电策略提升了配送效率和车辆满载率，减少了配送车辆使用数量，从而降低了配送总成本。

1 数学模型

1.1 问题描述

车辆从配送中心出发，对顾客进行商品配送，并在充电站对车辆进行充电，直至完成所有配送任务回到配送中心，该问题的示意如图1所示。

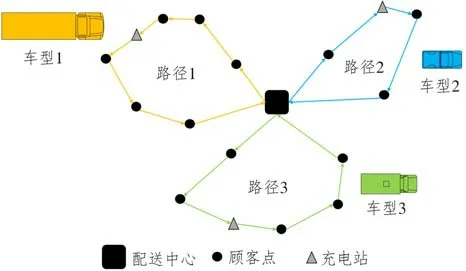
图1 多车型纯电动汽车车辆路径规划问题示意图

模型考虑电动汽车电量约束、行驶里程约束、电动汽车容量约束、顾客点时间窗约束，以最小化固定成本和可变成本为目标函数，并做如下假设：

（1）配送中心具有多种电动汽车，不同车型固定成本、单位里程使用成本不同，但数量均充足，所有车辆从配送中心出发，完成任务后返回配送中心。

（2）车辆能耗与行驶距离成正比，且车辆保持匀速行驶。

（3）充电速率固定，充电电量与时间成正比。

（4）充电站内充电桩无数量限制，多辆车可以同时充电。

（5）早于顾客时间窗下界或晚于顾客时间窗上界，均无法服务。

（6）所有顾客点均被服务但仅被一辆电动汽车服务。

1.2 变量说明

N=C∪P表示配送网络节点，其中C为顾客点集合，P表示充电站集合；考虑网络流模型流平衡约束，将每个充电站拓展出l个虚拟充电站，并定义所有虚拟充电站集合为P′。0 表示配送中心，n+1 表示虚拟配送中心，定义N0=N∪{0}，Nn+1=N∪{n+1}，包含虚拟充电站的集合分别记作N′0，N′n +1。本研究问题考虑多车型，定义车型集合V，车型v载重、满电续航里程、充电速率、单位里程可变成本、使用固定成本分别为W v、Bv、ηv、αv和f v；节点i到j的距离为dij，行驶时间为tij，则车型v通过弧(i,j)的可变成本可表示为cij=αv·dij；车辆在节点i最小剩余电量所对应的续航里程为min{dij,j∈Por{0,n+1}}；需求量为ϖi的顾客点时间窗约束为[lbi,ubi]；其服务时间为si。ai为车辆到达节点i的时间；bi为车辆到达i处的剩余里程；wi为车辆到达节点i的剩余容量；ρi为车辆在充电站i充电而增加的续航里程；为车辆v是 否经过弧(i,j)，经过为1，否则取0。

1.3 多次部分充电策略下的多车型电动汽车车辆路径优化数学模型

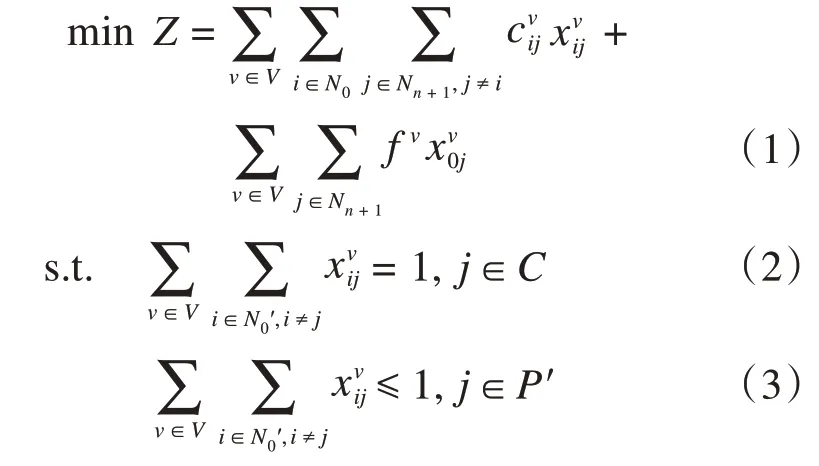
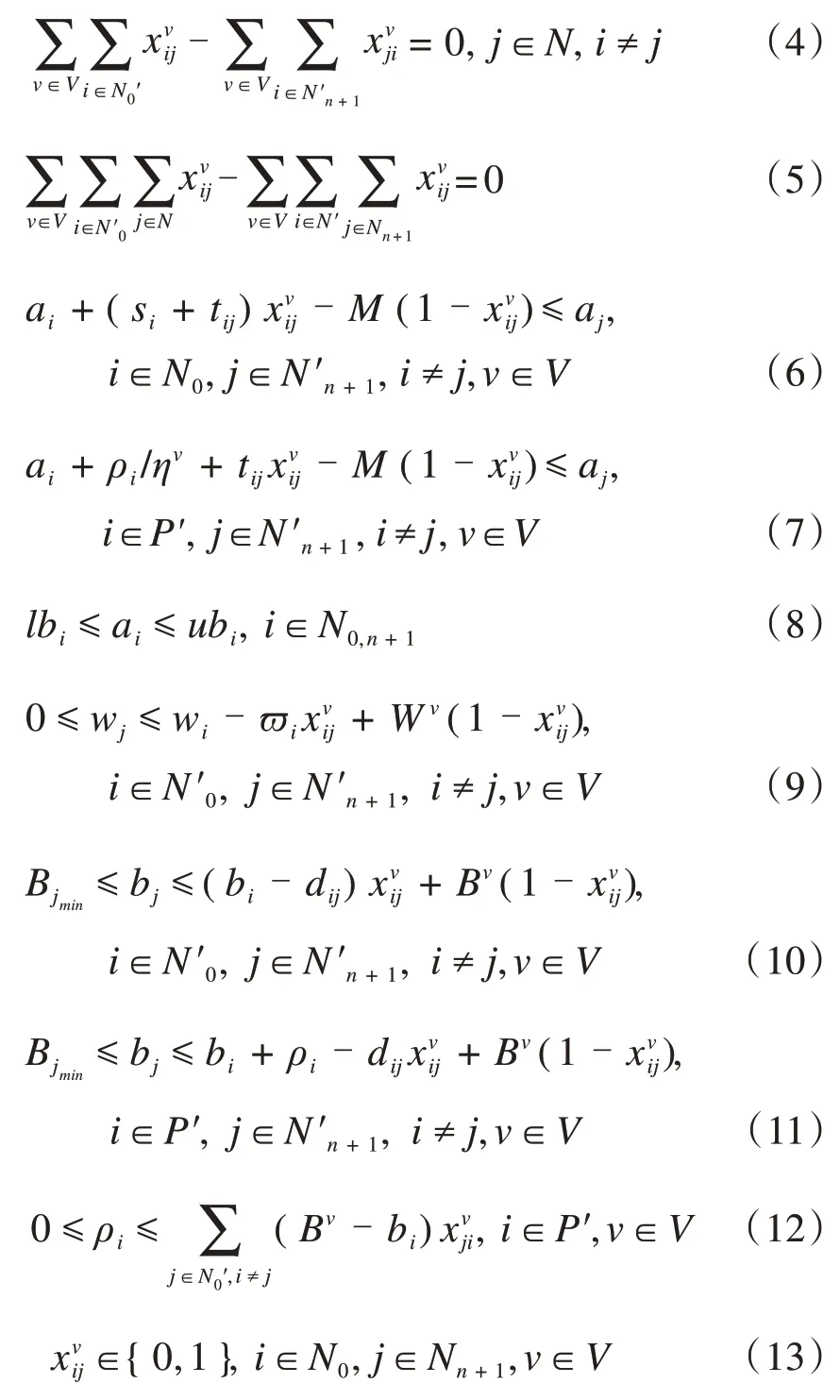
式（1）～（13）建立了多次部分充电策略下的数学模型，其中目标函数（1）表示完成配送任务总成本最小，包括车辆行驶的可变成本和使用的固定成本；公式（2）表示一个顾客有且只能有一辆车对其服务；公式（3）表示每个虚拟充电站至多服务一辆电动汽车，公式（4）表示经过节点的流平衡约束；公式（5）表示从配送中心出发的车辆数等于回到配送中心的车辆数；公式（6）和（7）分别表示车辆不进行和进行充电操作时节点间的时间关系，具体来说，如果i不是顾客点，则到达j的时间不早于电动汽车到达i的时间加上在节点i的充电时间与弧(i,j)的行驶时间；公式（8）表示车辆开始服务时间必须在顾客时间窗内；公式（9）表示车辆行驶过程中的容量约束；公式（10）和（11）分别表示车辆不进行和进行充电的行驶里程；如果车辆不进行充电，则其从节点i行驶至节点j后的剩余电量里程不大于节点i处的剩余电量减去弧(i,j)的长度，反之则加上节点i处的充电里程；公式（12）表示车辆的充电电量约束，在节点i的充电电量不能超过电动汽车电池总容量；公式（13）为0-1决策变量。

2 局部搜索增强的自适应大规模邻域搜索算法

2.1 算法设计

自适应大规模邻域搜索算法（Adaptive Large Neighborhood Search，ALNS）[14]是由大规模邻域搜索算法发展而来的，允许在同一搜索中使用多个摧毁算子和重建算子。在迭代过程中，算子使用的频率是通过其权重确定的，并在求解过程中动态调整。通过多个摧毁算子和重建算子对现有解进行操作，得到现有解的邻域，本文在此基础上对邻域进行局部搜索（Local Search，LS）操作以增强寻优能力。ALNS-LS的具体方法如下：

Step1 生成初始可行解；

Step2 根据算子权重选择摧毁算子和重建算子；

Step3 对解进行摧毁-重建-局部搜索操作；

Step4 根据新解的质量更新算子权重；

Step5 重复Step2～Step4，直至满足终止条件。

2.2 初始解的生成

ALNS-LS 作为启发式算法的一种，初始解的质量尤为关键，高质量的初始解可以提升求解速度，但往往构造时间较长。因此权衡初始解的构造时间和质量就显得尤为重要。

本文采用沿线插入算法进行初始化。定义由于时间约束而不能被同一辆电动汽车服务的任意顾客点集合为S(Ci)，并定义S(Ci)的并集为S(C)，同时定义路线Ri中所有顾客的近邻顾客点的并集为N(Ri)。在近邻的定义中，由于不考虑物流车在顾客点处的等待成本，因此直接采用物流车旅行时间作为近邻的计算标准。近邻顾客点数量的选取也十分重要，太大会产生较高的计算成本，需要根据计算规模的不同灵活地进行调整。算法具体步骤如下：

Step1 根据约束在所有待规划顾客点U(C)中计算S(C)；

Step2 随机选择S(Ci)∈S(C)，ci∈S(Ci)和v∈V初始化路线Ri，如果S(C)为空，则随机选择ci∈U(C)和v∈V初始化路径Ri，并更新N(Ri)；

Step3 遍历ci∈N(Ri)，如果当前路径有可行插入位置，则更新Ri，U(C)，N(Ri)；否则，Ri即为一个初始解子集，如果S(C)和U(C)为非空，转Step1。

2.3 摧毁算子

摧毁算子（D={di|i=1,…,m}）在构建邻域中起到至关重要的作用，每个算子di被选择的概率为，其中μdi为算子di的权重。考虑算法搜索的深度与广度，本文采用以下四种摧毁算子：

（1）随机删除

从路径中随机选择多个顾客点直接删除，并记录于待规划顾客点集合。

（2）最差删除

路径上每增加一个顾客点，一定会造成总成本某种程度上的增加，定义顾客点i的服务成本为icost=，其 中和分别表示路径中服务顾客点i和不服务顾客点i的成本。最差删除是将路径上服务成本k最大的顾客点移除。

（3）基于距离删除

车辆从配送中心出发有序访问顾客点或充电站构成的路径是由多个弧组成，计算每个弧的长度，并删除起终点不是配送中心或充电站且距离最长的弧。

（4）基于角度删除

车辆配送的路径所围成的区域多数是扇形区域。如果路径上的顾客配送距离都比较近，那么围成的扇形区域的角度大半径小，反之围成的扇形区域角度小半径大。基于角度的删除是通过计算路径服务顾客所围成扇形的夹角与半径来确定要删除的顾客点。

2.4 重建算子

重建算子（R={ri|i=1,…,l}）同摧毁算子一样在构建邻域中起到重要的作用，每个算子ri被选择的概率为，其中μri为算子ri的权重。本文采用以下三种重建算子：

（1）成本最小插入

遍历待规划顾客集合，每次从其中选出一个顾客重新插入路径，直至待规划顾客集合为空。定义Δc(i,r)为顾客点i插入路径r中最优位置后的成本，则顾客的最优插入成本为iinssertcost=min{Δc(i,r)|r∈Ω}。

（2）后悔插入

每一个顾客点在每一条路径上均有最小增加费用Δe(i,r)，下一个候选插入点的确定公式为：

式中：U(C)为待规划顾客点的集合；Δe(i,r*)表示顾客点i插入的最低费用增加，且最低费用对应的路径为r*；Δe(i,rj)表示除最低费用对应路径外其他路径中的最低插入费用；z为顾客点i可插入路径的个数。通过遍历待规划顾客，将其插入各自最低费用路径中的最优位置。

（3）充电站最优插入

在路径合适位置插入充电站以延伸电动汽车的行驶里程，提升电动汽车使用效率。找到不满足里程约束的顾客点并在其之前插入充电站，如果该点无法插入充电站则充电站依次往前移动直到找到合适的位置。

2.5 局部搜索

本文对ALNS 算法进行摧毁和重建操作后的解应用邻域搜索算法以增强算法的寻优能力，具体采用以下六种操作：

（1）Swap

Swap 算法是路径间搜索，通过交换路径r1和路径r2的部分连续有序顾客点来实现，Swap(p,q)表示将路径r1上的p个连续有序顾客点与路径r2上的q个连续有序顾客点进行交换。

（2）Shift

Shift 算法是路径间提升算法，将路径r1的部分顾客转移到路径r2上。例如Shift(n,0)表示将r1的n个连续顾客点转移到r2，通常包括Shift(1,0)，Shift(2,0)两种情况。

（3）Exchange

同样为路径间搜索，操作与Swap 相似，但不强调数量。路径r1和路径r2分别选择一个分割点，对分割点后的路径进行交换。

（4）2-Opt

2-Opt 为路径内搜索，通过移除路径内任意两个不相邻的弧后，重新插入两条新弧构成路径。

（5）充电站位置优化方法

由于电动汽车受里程限制较大，因此合理的充电策略可以有效地延长电动汽车行驶里程，实现降本增效的目标。通过向路径中插入虚拟充电站（增加充电次数），避免了违反车辆续航里程约束；或移除已存在路径中的虚拟充电站（减少充电次数），降低车辆因不必要的充电行为而增加的配送成本。

（6）车型优化方法

在满足路径中顾客点容量约束和续航里程约束的前提下，迭代过程中以一定的概率调整车型的指派关系。该概率随着算法迭代次数的增加而降低。

2.6 权重的更新

ALNS中多种不同摧毁-重建算子的应用在迭代过程会产生不用优化效果，所以在每次迭代结束后各个算子的权重采用以下更新方式：

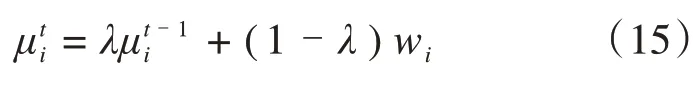
其中是第t次迭代时算子i的权重，是0-1 之间的参数，wi是算子当前的得分，由当前解与新生成解的优劣决定。算子生成新解的质量越高，其得分越高，具体如下所示：

3 算例分析

3.1 算例设计

以Solomon算例[15]为基础，合理地增加充电站信息。不同类型算例车辆信息如表1所示。

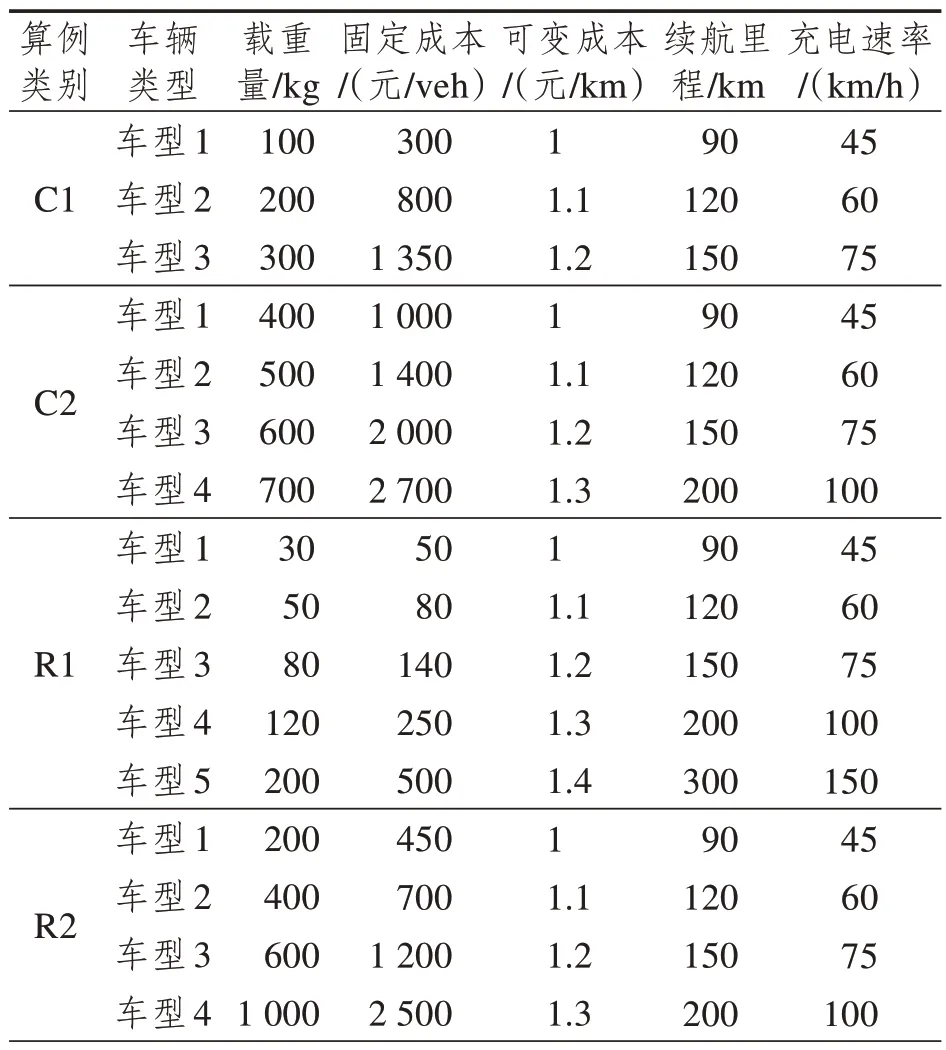
表1 车辆信息表

续表1

3.2 算法有效性分析

首先检验ALNS-LS 算法的有效性，在顾客规模为50，车型信息为R1 的10 组算例，设置迭代次数为200 次，运行时间为3 600 s，分别对比完全充电策略和部分充电策略。求解的结果过如表2所示。

算例以“类别_顾客点数量_充电站点数量_实验次数”命名，解以“车型编号：该车型数量，车型编号：该车型数量，……”表示。从表2 可以看出，完全充电策略算例均可以在3 600 s 内求解，算法性能较好。7 组算例部分充电策略配送成本优于完全充电策略，平均节约成本12.6 %。但值得注意的是有3组算例结论相反，其主要原因是部分充电策略在优化过程中需要决策每辆车在充电站的充电电量，因此每次迭代所用时间更长，在相同时间内对解空间的搜索不够充分。

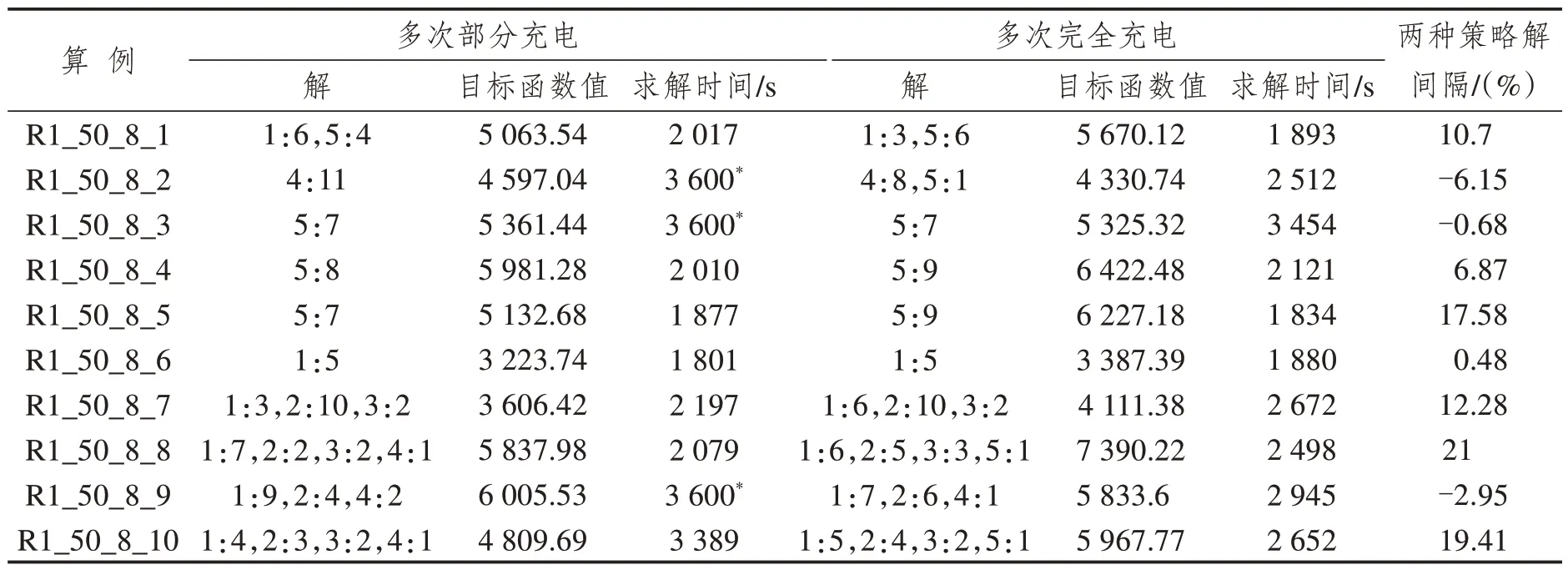
表2 算例结果（1）

为了进一步验证部分充电策略在配送成本上的优越性，本文分别利用C1、C2、R1、R2、RC1、RC2 共6 种车型，设计顾客规模为20、50 和100 的算例进行求解，实验结果如表3所示。

表3 算例结果（2）

从表3 中可以看出，13 个算例中12 个算例部分充电策略的配送总成本优于完全充电策略，就求解耗时而言，部分充电策略用时更久。算例规模与时间间隔百分比没有明显的单调关系，但是随着顾客点的增加使得车型组合更为复杂，部分充电策略在成本上的优势也更为明显。

3.3 算法收敛性验证

为了进一步验证算法收敛性和鲁棒性，从每种类型算例中各选取一组顾客数量规模为50，充电站为8 的算例，共6 组算例。设置终止条件为迭代次数到达500 次，运行时间为3 600 s，在部分充电策略下对每组算例求解5次，得到最优迭代曲线和平均迭代曲线，以及最优解迭代过程中算例车辆配置信息。以C1_50_8_1 为例绘制收敛信息图和车型配置信息图，分别如图2 和图3 所示。算法收敛较快，在40代后结果趋于稳定，最优曲线与平均曲线之间间隔较少，仅为6.21%，算法鲁棒性较好，值得注意的是车型3的固定成本和可变成本相对较高，因此在车辆数量充足的情况下未出现在最优解中。

图2 收敛信息图

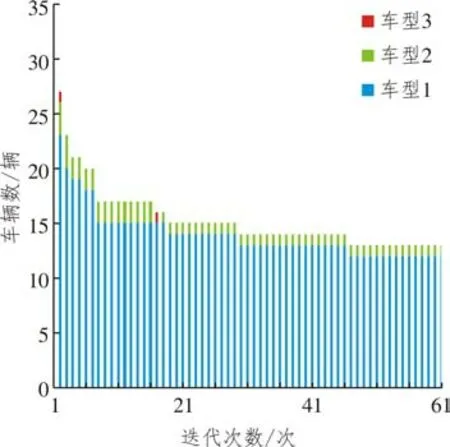
图3 车辆配置信息图

3.4 算例仿真

选择规模为100 的Solomon 的RC2 型算例，从中随机选取50 个节点作为顾客点，9 个节点改造为充电站构造算例。算例的配送中心点、顾客点、充电站的坐标信息、时间窗、服务时间及需求量见表4。

表4 配送中心、顾客点和充电站节点信息

续表4

在完全充电和部分充电两种策略下对问题进行求解，分别得到配送路线方案如表5 与表6 所示，方案包括具体指派关系及顾客访问顺序，总成本由单位成本和车辆使用成本构成，距离为该路径对应的行驶距离，满载率（%）为车辆所载顾客需求的总重量比对应车型的最大载重量。

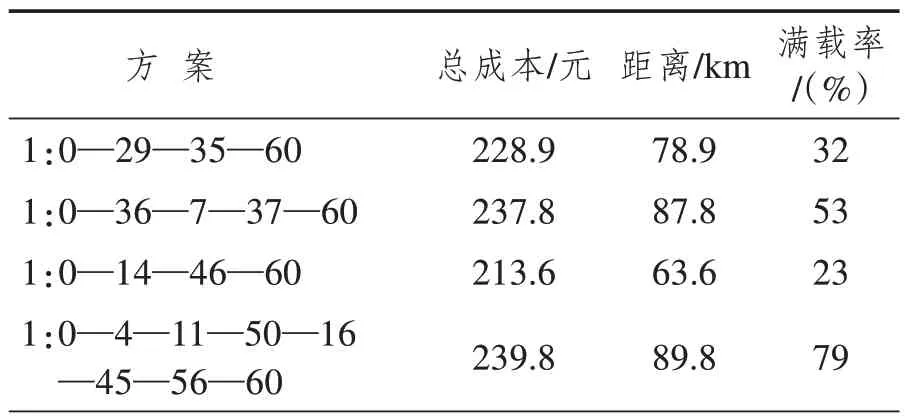
表5 完全充电策略下配送路径优化方案

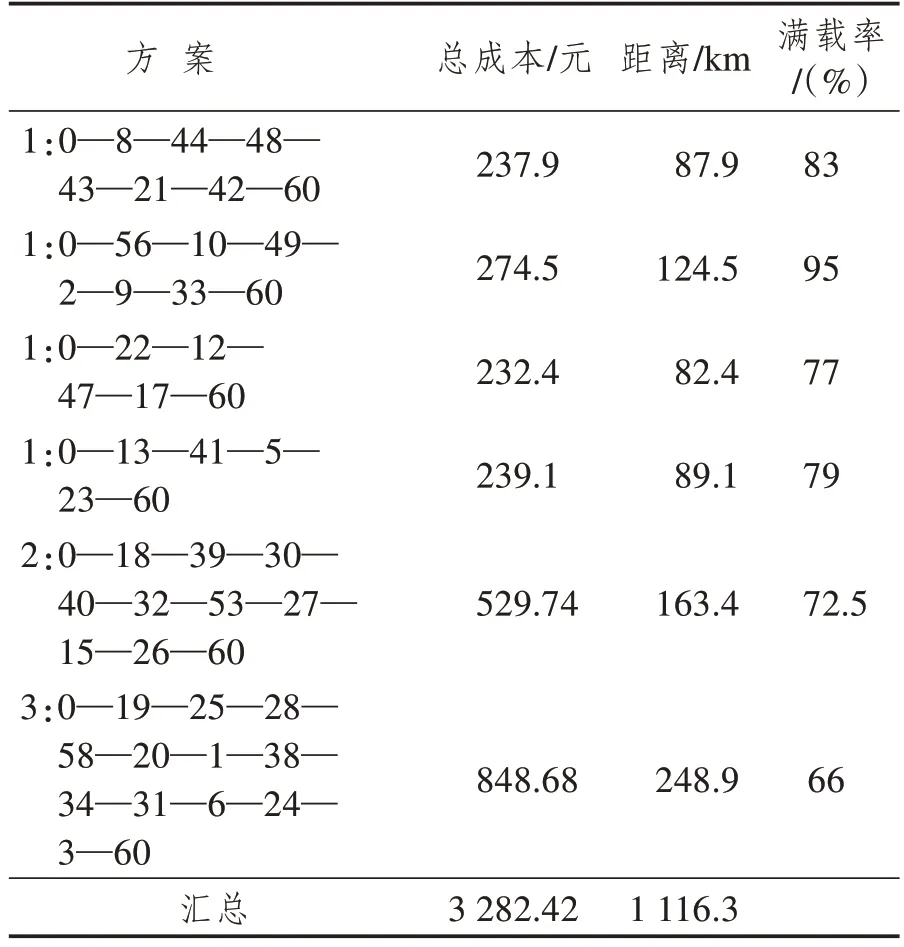
续表5

表6 部分充电策略下配送路径优化方案

完全充电策略下使用1型车8辆，2型车1辆，3型车1辆，共计10辆，部分充电策略下使用1型车7辆，2 型车1 辆，3 型车1 辆，共计9 辆，后者要比前者少使用一辆电动汽车。虽然两种充电策略下的总成本相差不大，但是部分充电策略下的80%以上车辆的满载率超过60%。两种配送路径方案可视化分别如图4（a）和（b）所示。

图4 配送路径方案可视化图

3.5 灵敏度分析

物流企业电动汽车的使用成本相对固定，是否选择使用其完成配送任务主要取决于它们的可变成本。现在考虑当电动汽车固定成本一定时，可变成本变化对数值实验结果的影响。构造顾客点数量为20，充电站数量为3的算例。选择车辆信息类型为R1 的多车型集合，控制其他车辆可变成本一定，在考虑多次部分充电策略下，设置3 型电动汽车的单位可变成本分别为1.2，1.3，1.4，1.5 进行求解，其灵敏度分析实验结果如表7所示。

表7 灵敏度分析结果

从表7 可以看出，所有算例均在660 s 内得到计算结果，配送总成本随着车型3单位可变成本的上升而增加，最优解中出现车型3的数量也随之减少，但是对于给定的算例，车型3 的数量在减少到一定程度时将保持稳定，可变成本和固定成本没有单调性。然而对于最优解中不包含车型3 的算例而言，车型3单位可变成本的扰动不会对最优解以及最优值带来任何影响。

4 结束语

本文针对电动汽车运行里程受限，在模型中考虑部分充电策略，利用电动汽车使用的固定成本和单位里程可变成本构建目标函数，考虑车辆异质问题，建立了多车型电动汽车车辆路径规划模型，并设计局部搜索增强的自适应大规模邻域搜索算法进行求解。通过算例分析验证算法的有效性和收敛性，并且对比了多次部分充电策略和多次完全充电策略对配送成本的影响。研究结果表明，部分充电策略的使用可以在一定程度上降低配送成本、减少配送车辆的使用数量、提升电动汽车的满载率。然而本研究没有考虑交通网络状态对电动汽车运行的影响，进一步研究可以引入基于拥堵情况的电能消耗、突发情况等复杂场景，从而构建含有不确定参数的鲁棒优化模型。