高峰期城市轨道交通列车跳站运行优化
吴文祥,赵浩淋,周慧娟,陈 智
(北方工业大学,城市道路智能交通控制技术北京市重点实验室,北京 100144)
0 引言
随着大城市轨道交通高峰期大客流的常态化,轨道交通运营管理面临着巨大的压力与挑战,运营部门采用扩大列车运力、增加发车频率、实行进站限流等一系列措施来缓解高峰期的客运压力。传统“站站停”轨道交通列车运行模式虽然可以满足乘客基本的出行需求,但是由于忽略了不同车站客流时空分布特征,影响了列车运力配置的效果,造成乘客旅行时间增加、列车运行时间增加等问题。因此,本文基于动态客流时空分布特征,以最小化乘客总旅行时间和站台乘客最大数量为目标,提出了一种基于跳站运行模式的轨道交通列车运行图优化方法,实现列车跳站运行方案与实时大客流的精准匹配。轨道交通列车跳站运行模式(也称跳停模式),不同于“站站停”的运行模式,是指列车只停靠线路的若干特定车站,而其他站只通过不停车。虽然跳站运行增加了列车运行组织的难度,也增加了站台候车乘客的平均等待时间,但是跳站可以减少列车加速、减速以及停站的次数,从而缩短了乘客的车内旅行时间,减少了列车站间运行时间,提高车辆周转率,也减少列车能源消耗。美国、法国、英国、德国、日本等国家早在20世纪中叶就已在城市轨道交通中采用列车跳站模式[1]。国内上海、深圳、广州等城市的一些轨道交通线路预留了越行配线,已采用或准备采用列车跳站运行模式。
列车跳站优化是铁路组织优化的重要组成部分,已引起了国内外学者的广泛关注和深入研究。考虑静态客流需求,郑锂等[2]建立了一个列车跳站运行非线性整数规划模型,并使用了禁忌搜索算法对模型进行求解。Wang 等[3]针对单向地铁列车跳站运行调度问题,以最小化乘客等待时间和列车能源为目标,构建了一个基于跳站策略的非线性规划模型,设计了双层优化算法,并在北京亦庄线进行了算法验证。Salama 等[4]提出了列车跳站运行策略下的最大化乘客直达数量的非线性整数规划模型,并运用穷举法求得最佳跳站策略。Abdelhafiez 等[5]首先提出了一种OD 矩阵生成方法,再以最小化乘客平均旅行时间为目标,建立了一个列车跳站运行非线性整数规划模型,最后用生成的OD 矩阵验证了跳站运行的有效性。Lee 等[6]提出了四种地铁跳站运行策略,以列车总运行时间为目标,建立非线性整数规划模型,对四种地铁跳站运行策略进行对比分析。Niu等[7]考虑了地铁列车的跳站模式,为动态客流需求下的列车跳站运行问题建立了非线性整数规划模型,并采用GAMS/AlphaECP 对模型进行求解。Shang 等[8]基于乘客的公平性原则,建立了地铁跳站运行线性整数规划模型,并设计了有效的拉格朗日松弛算法。Zhao 等[9]研究了动态客流需求下单向轨道线路的列车跳站策略,以乘客出行时间成本和列车运营成本为优化目标,建立了非线性整数规划模型并设计了遗传算法,最后以广州地铁八号线为例,验证了模型和算法的有效性。陈吉怀和赵星[10]以最小化乘客总候车时间为目标,提出了一种可预见大客流下的列车跳站与列车时刻表优化联合模型,采用一种改进的遗传算法求解模型,并借助南京地铁S1号线的早高峰数据验证模型与算法的有效性。孟凡婷等[11]引入列车运行图与车站限流的相关决策变量,以提高列车运行效率、减少客流乘车延误人数为优化目标,建立轨道交通列车运行与车站限流协同优化的双目标整数非线性规划模型,运用时间重构和大M 方法将原模型中的非线性约束进行线性化处理,得到一个新的整数线性规划模型,并利用CPLEX 软件求解。此外,还有一些学者研究地铁运行中断或不确定情形下的列车跳站运行问题。Altazin 等[12]研究了中断地铁线路上的跳站运行策略问题,提出了一个整数线性规划模型,以实现地铁线路恢复时间和乘客等待时间最小化。Gao等[13]在铁路运行中断后,考虑了动态客流的过饱和情况,结合跳站策略设计了一种地铁线路恢复期列车运行图再优化模型,达到减少乘客站台等待时间的目的。Jamil等[14]考虑了在不确定客流情况下,结合跳站运行策略,提出了一种最小化线路总列车运行时间的鲁棒性数学模型,并设计了分解算法与模拟退火算法相结合的求解算法。
综上所述,国内外学者对列车跳站模式进行了广泛深入地研究。但是,目前大多数研究仅考虑单向线路的跳站策略,没有刻画列车跳站运行导致乘客的复杂换乘行为[3,7,8,14,15]。虽然有些研究考虑了双向线路的列车跳站策略,但是大多数模型不允许乘客换乘,导致列车跳站的机会较少、列车运行时间降低不明显[13];当然,也有少数模型允许乘客换乘,但是假设乘客换乘的等待时间只与车头时距有关,与站台人数无关[4-6,16]。总之,现有的列车跳站优化模型还不能很好地跟踪乘客的动态决策过程、乘客在各站台的上下车过程以及乘客的动态换乘行为,即不能很好描述客流动态分配过程。可见,现有的列车跳站优化模型难以对客流指标及其目标函数进行精细化刻画,这影响了列车跳站优化的效果。
事实上,每个起点和终点(OD 对)的动态客流分配过程恰恰是制定列车停站计划的关键决策依据[17]。此外,高峰期轨道交通的客流需求比较大,而且车站客流呈现明显的峰值特征,这意味着:(1)客流等待时间与站台人数有关,站台人数越多,客流等待时间越长;(2)客流等待时间与列车剩余空间有关,停靠列车剩余空间越小,站台客流的等待时间就越长;(3)客流等待时间还与乘客到达时间有关,越靠近峰值,等待时间越长。可见,客流乘车方案的选择不仅与列车跳站方案、时刻表有关,而且还与乘客到达时间、站台客流状态以及列车运行状态有关。基于以上分析,本文在精细化描述客流指标的基础上,以最小化乘客总旅行时间及最大站台人数为目标,构建一个双向轨道交通线路的列车跳站运行整数规划模型,实现列车运力与客流时空分布的精准匹配。本文主要有以下三个方面的贡献:首先,不同于以往大多数研究,综合考虑了乘客的等待时间、换乘时间与车内时间,描述了列车跳站运行导致乘客的同向换乘行为和反向换乘行为[18];其次,高峰期大客流可能导致乘客无法登上当前的列车,即乘客的愿意上车人数和实际上车人数不相等,因此,本文结合乘客的换乘行为和动态决策过程,计算当前列车各OD 对乘客的愿意上车人数,然后根据列车的剩余空间计算各OD 对乘客的实际上车人数,以此为基础,完成站台人数和车内人数的更新;最后,为了避免列车灵活跳站导致站台乘客数量过大、等待时间过长,将最大站台人数作为惩罚值引入模型的目标函数,并基于上述动态客流分配方法,对乘客总旅行时间和站台最大人数进行精细刻画。
1 列车灵活跳站优化模型
1.1 问题描述
本文研究双向城市轨道交通线路的列车跳站运行优化问题,轨道交通线路的物理结构如图1所示。该轨道交通线路有上行、下行两个方向,各方向共有N个车站、N-1 个区段,上行方向车站编号j(j=1,2,…,N)与下行方向车站编号N+1-j对应同一个站台,线路两端由折返线与发车站相连,列车沿两侧的折返线到达始发站后,沿预设方向运行。

图1 轨道交通线路物理结构
为实现列车运力与客流的精准匹配,本文采用列车灵活跳站(Flexible Skip-Stop)模式。为方便研究,本文作出以下假设:
假设1 根据历史的刷卡数据和其他数据,可以精确预测乘客的出行需求,即模型中的客流动态OD是已知的。
假设2 高峰期列车发车间隔是固定的,站台有足够大的空间容纳已进站的乘客。
假设3 乘客上车遵循先到先行原则,即先进站的乘客先乘车,滞留乘客在下次列车到达时优先乘车。
假设4 乘客换乘在同站台进行,不单独计算乘客的换乘步行时间,将换乘步行时间计入乘客等待时间。
假设5 在满足列车安全约束和列车停站约束的条件下,除始发站和终点站外,允许列车不停车通过任意中间车站,即列车是灵活跳站运行。
假设6 同道路交通确定性用户均衡模型一样,假设轨道交通线路的所有乘客都选择最小旅行时间的出行方案。
1.2 符号和定义
(1)索引和参数
N:轨道交通线路的车站数量,N>3;
i,j,v:地铁车站编号,i,j,v=1,2,…,N;
vjm:列车m停靠站j的下个停靠车站;
M:计划期内上行(下行)发出的列车数量;
m,k,u:列车的编号,m,k,u=1,2,…,M;
ujm:站j停靠列车m的上一个停靠车次;
f:方向编号,f=1 为上行方向,f=2 为下行方向;
Cm:列车m的最大容量(最大载客量);
H1:同方向相邻两列车离开同一车站的最小时间间隔;
H2:同方向相邻两列车到达同一车站的最小时间间隔;
H3:同方向在同一车站相邻两列车到站与离站的最小时间间隔;
Hf:f方向的列车发车间隔;
T:计划期;
(2)时间参数
WT:轨道交通线路的乘客总等待时间;
VT:轨道交通线路的乘客总车内时间;
PN:最大站台人数;
β1,β2,β3:分别是WT、VT、PN的权重系数。
(3)动态客流参数
pjif(t):f方向在t时刻乘客到达车站j且出站为车站i的客流到达率;
wjif(t):f方向在截止到t时刻从车站j到车站i的潜在上车乘客数量;
wjf(t):f方向在截止到t时刻车站j的潜在上车乘客数量;
(4)决策变量
1.3 列车跳站运行相关约束
(1)列车到发时间约束
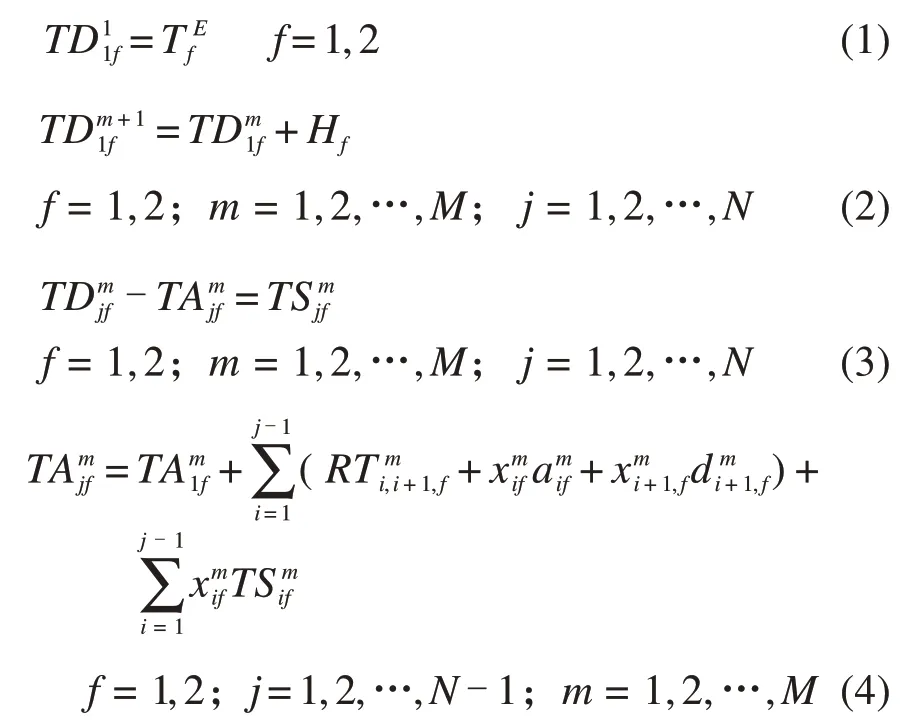
约束(1)为计划期内各方向第一辆列车的发车时间。约束(2)、(3)分别是各方向各列车的发车时间间隔约束和各站的停站时间约束,如不停靠车站j,则=0。约束(4)是各方向列车到达车站j的时间等于列车的首站到站时间、从首站到车站j的列车站间运行时间与从首站到j-1 站的所有停站时间之和。公式(4)表明列车跳站不仅减少了列车停站时间而且还减少了列车站间运行时间。
(2)列车停站约束
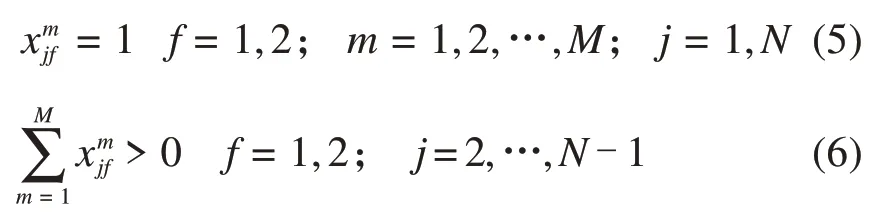
约束(5)确保所有列车都停靠首末站,约束(6)确保在任意中间车站j都有列车停靠。
(3)停站时间约束

约束(7)确保列车m在车站j的停站时间不超过最大停站时间且不小于最小停站时间。
(4)安全车头时距约束

为了确保列车安全运行,约束(8)是指在同一站的相邻车次到达时间间隔不小于H1;约束(9)保证同一站的相邻车次出发时间间隔不小于H2;约束(10)保证同一站的后一辆列车到站与前一辆列车出站的时间间隔不小于H3。H1、H2、H3均为安全时距。
(5)车辆容量约束

约束(11)是指任意时刻列车m的车内人数不大于其最大容量。
1.4 精细化客流约束
为了便于计算,本模型只统计列车进站、离站时刻的相关客流指标。
(1)乘客的下车数量
f方向列车m离开j站前,乘客在车站j从列车m下车的人数等于f方向乘坐列车m在车站j之前上车并在车站j下车出站的乘客总人数,f方向乘坐列车m在车站j下车同向换乘去目的地车站的乘客总人数,f方向乘坐列车m在车站j下车反向换乘去目的地车站的乘客总量以及f方向乘坐列车m在车站j下车反向换乘去目的地车站的乘客总量之和。计算公式如下:
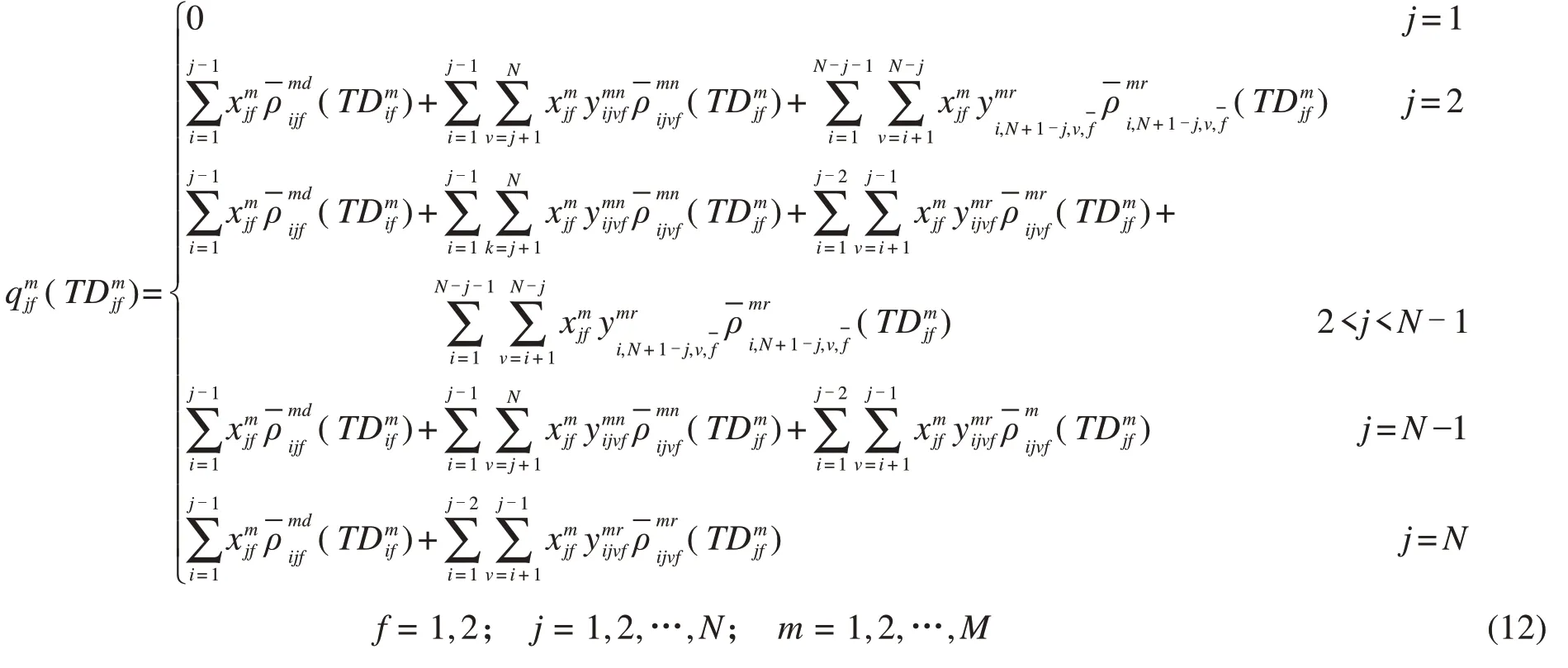
公式(12)中若f=1,则=2;若f=2,则=1。
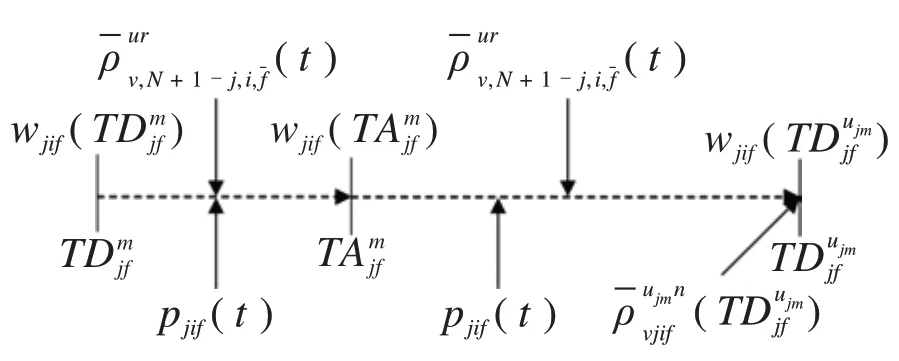
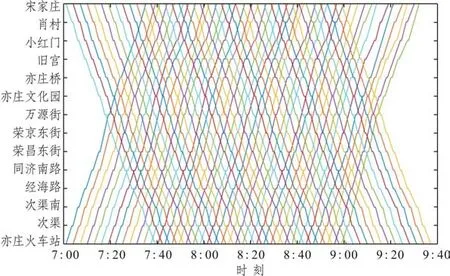
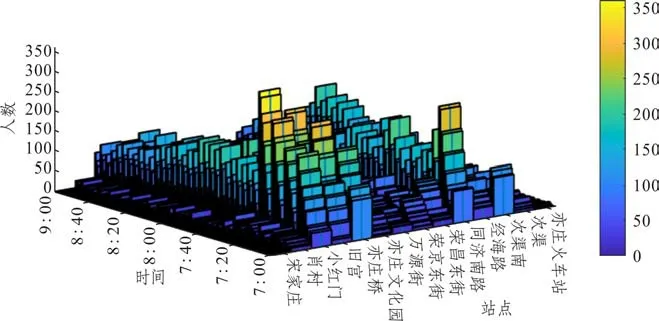
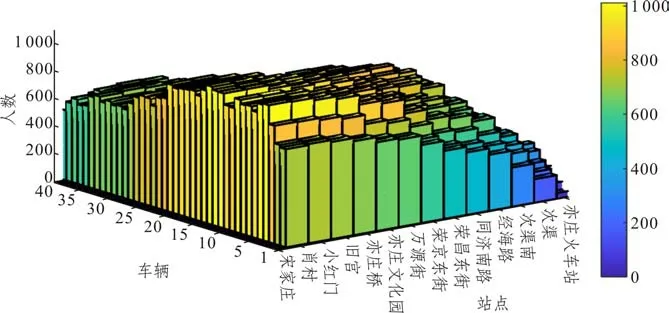
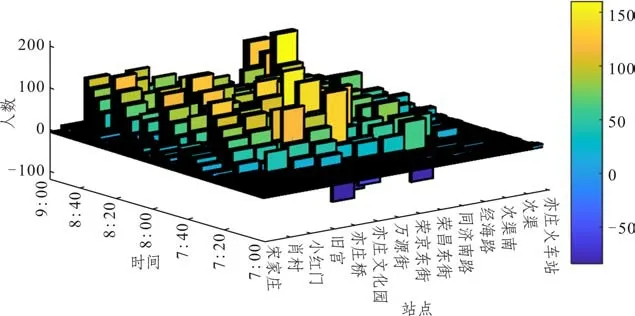
为了便于理解,下面用示意图解释公式(12)。从图2可以看出:f方向从车站j(2 另外,从图2 也能看出:f方向列车m在首发站无乘客下车。f方向第二站无反向换乘乘客,否则乘客的终点站是首发站,显然不可能。同理,倒数第二站方向无反向换乘乘客。显然,f方向末站只有f方向下车出站的乘客和f方向下车反向换乘的乘客。 图2 在车站j(2 (2)潜在上车乘客数量 列车m离开车站j前潜在上车乘客数量等于列车m到达车站j时站台潜在上车乘客数量、列车m在车站j停靠时段内进站到达站台人数与列车m在车站j停靠时段内f—方向在车站j下车反向换乘的乘客数量之和,如图3所示。 图3 列车m离开车站j前潜在上车乘客示意图 计算公式如下: 列车m到达车站j时,潜在上车人数等于列车ujm离开车站j时站台剩余上车人数,从列车ujm离开车站j至列车m到达车站j时间段内的f方向进站人数,从列车ujm离开车站j至列车m到达车站j时间段内的方向在车站j下车的反向换乘乘客人数以及在车站j从列车ujm下车的同向换乘乘客人数之和,如图3 所示。特别指出:从列车ujm下车同向换乘乘客不可能再上列车ujm,只能是列车m的潜在上车乘客。因此,潜在上车人数的计算公式如下: (3)乘客的实际上车数量 显然,列车m的潜在上车乘客数量不一定等于实际上车人数,这有两个原因:①乘客不一定愿意乘坐当前列车m;②即使乘客愿意乘坐当前列车m,列车m的能力约束也不能保证所有愿意上车的乘客都能上车。为了计算乘客实际上车数量,首先要描述乘客是否愿意乘坐当前列车m。如图2所示,f方向乘客可能存在三种乘车方案:①乘客直达目的地;②乘客需同向换乘到达目的地;③乘客需反向换乘到达目的地。乘客从三种乘车方案中选择旅行时间最小的乘车方案。计算各乘车方案的旅行时间都是将当前列车m离开车站j的时间当作基准时间,之前的时间都可看作沉没成本,对当前的决策不产生影响。根据列车时刻表,下面分别计算乘客各种乘车方案的旅行时间。 (a)乘客直达 从车站j到车站i的乘客如果选择次列车直达目的地,则其旅行时间为: 公式(16)表明,乘客选择列车k直达目的地,列车k必须停靠车站j和车站i(即>0),而且列车k必须满足k≥m。 (b)同向换乘 公式(17)中乘客首先选择列车k到达换乘车站,这要求列车k必须停靠车站j和车站v但不停靠车站i(即>0 且=0),而且列车k必须满足k≥m。既然是同向换乘,乘客选择的换乘车站v必须满足j (c)反向换乘 与同向换乘一样,反向换乘的乘客首先选择列车k到达换乘车站v,这要求列车k必须停靠车站j和车站v但不停靠车站i(>0 且=0),而且列车k必须满足k≥m。不同于同向换乘,公式(18)中乘客选择的换乘车站v必须满足v>i,而且乘客选择的从换乘车站到目的地车站的反向车次u必须晚于列车k到达车站v(即,而且反向车次u必须停靠车站v和i(即 显然,从车站j到车站i的乘客选择直达、同向换乘、反向换乘方案中旅行时间最小的车次,即: 如果k=m(即,则从车站j到车站i的乘客选择乘坐当前列车m,具体乘车方案如下: 特别指出:相对于道路交通系统,地铁系统运行是可靠的,列车跳站方案可在互联网、站台大屏及时向乘客发布,乘客可以获取所需信息进行动态乘车决策,选择当前最快乘车方案。地铁公司也可以基于乘客达到时间和列车跳站方案生成最快乘车方案,并通过手机APP向乘客推荐该方案。 根据得到的乘车方案,计算从车站j到车站i乘客愿意乘坐列车m的人数: 显然,j站乘客愿意乘坐当前列车m的总人数为: 停靠车站j列车m的剩余空间由列车最大容量与列车m在车站j的下车人数之和减去列车m到达车站j时的车内人数,则: 列车m在车站j实际上车人数等于愿意乘坐当前列车m的乘客人数与车内剩余空间的最小值,即: 在计算车站j实际上车人数之后,再计算各OD 实际上车人数。由车站j到车站i的乘坐列车m的实际上车人数等于从车站j到车站i乘客愿意上车的人数与在车站j愿意上车的总人数的比值乘以列车m在车站j实际上车人数[13],则: 简而言之,OD 对(3,5)乘客和OD 对(3,9)乘客,按需求比例各有20 人乘坐当前列车m直达目的地车站,未上车的乘客在下一辆停靠车站3的列车到站后再做决策。 从车站j登上列车m且出站为i的乘客人数为: 更新站台潜在上车乘客数量: 更新列车m在车站j离站时的车内人数,车内人数等于列车m在车站j到达时的车内人数与从车站j登上列车m的实际上车人数之和减去在车站j的下车人数: 列车m离开车站j的车内人数等于列车m到达下一停靠车站时的车内人数,则: 本文从乘客的角度优化列车跳站运行方案,以最小化乘客站台总等待时间,乘客车内总时间以及最大站台人数为目标,下面分别给出它们的计算公式。 (1)乘客站台总等待时间 站台乘客总等待时间WT等于列车停站期间站台乘客等待时间,相邻两辆列车到站间隔期间站台剩余乘客等待时间与两辆列车到站间隔期间新进站乘客等待时间之和,具体计算公式如下: (2)乘客车内总时间 乘客车内总时间VT包括列车停站时车内乘客时间加上列车在区段内运行时车内乘客时间,计算公式如下: (3)站台乘客最大数量 在灵活跳站模式中列车停站没有规律,可能会造成某一个站台乘客的持续增加,为了避免站台客流过度拥挤,将最大站台人数作为惩罚引入目标函数,上行方向和下行方向的最大站台人数的计算公式如下: (4)列车跳站优化模型构建 基于上面刻画的目标函数和约束条件,引入权重系数β1,β2,β3,以最小化系统乘客总等待时间,乘客总车内时间和最大站台人数的加权和为目标,构建列车灵活跳站模型如下: 约束条件(1)~(31)。 本文所构建的模型是一个大规模非线性0-1整数规划模型。各列车都停靠首末站,其他中间车站列车都可以通过不停车,则上行方向或下行方向任意列车最大停站方案有2N-2个,M辆列车最大停站方案有2M(N-2)种组合。例如,上行方向N=20,M=40,上行方向共有240×18=2720个停站方案,解的空间规模极大,传统算法难以求解。混合蛙跳算法是一种新兴的群体智能优化算法,在处理具有复杂多峰的优化问题上具有良好的鲁棒性和全局收敛性。鉴于列车灵活跳停问题的规模和复杂性,本文在混合蛙跳算法(SFLA)的基础上提出改进的SFLA算法。本文对SFLA的改进体现在以下两个方面:(1)基于子蛙种群规模与子蛙群内部最大迭代次数之间的函数关系,更新不同子蛙种群的最大迭代次数;(2)在子蛙种群迭代中引入了安全约束判定,在不符合安全约束的最差解基础上,重新生成新的可行解,因为最差解中也有可能包含优秀的基因,以增加子蛙种群搜索的广度。混合蛙跳算法流程如图4所示。 图4 混合蛙跳算法流程图 步骤0 初始化。随机生成Spop个停车方案,组成方案集合pop(即青蛙种群),Spop是青蛙种群规模,种群最大进化次数是。设置子蛙群数量Q,每个子蛙群的集合subi(i=1,2,3,…,Q),即子蛙群中停车方案的集合,Ssubi(i=1,2,3,…,Q)是青蛙种群规模。设置子蛙群规模Ssubi和子蛙群内部最大迭代次数的函数关系=f(Ssubi)(i=1,2,3,…,Q),设置各子蛙群从青蛙种群取值比例α(0<α<1)。输入乘客到达率pjif(t)(任意i,j,f,t)。 步骤1 编码。每个停车方案χMN就是一个青蛙个体χMN,采用0-1 编码形式,单个青蛙个体由M×N个编码组成,每行代表一列车,每列代表一车站,1代表停站,0代表跳过车站。令种群进化代数ngen=1。 步骤2 计算客流参数。根据青蛙种群中χMN停车方案,计算上行和下行方向任意列车m在任意站j的到站时间和发车时间,按照约束条件(1)~(10)判断停车方案是否符合安全约束,将不符合安全约束的停车方案其适应度函数(目标函数)置为足够大的常数,转到步骤4。针对符合安全约束的停车方案,计算客流相关指标,下面是客流相关指标计算的具体步骤。 步骤3 计算适应度函数值。按照公式(32)~(34)计算乘客站台总等待时间WT、乘客车内总时间VT和最大站台人数PN,再按照公式(35)计算停车方案χMN的适应度函数值,即目标函数值Z=min (β1WT+β2VT+β3PN)。 步骤4 青蛙种群适应度计算终止判定。青蛙种群pop中每一个青蛙个体按照步骤2至步骤3重复迭代,得到青蛙种群pop中每个停车方案的目标函数值;否则,转步骤2 至步骤3 继续迭代,计算青蛙种群pop中停车方案的目标函数值。 步骤7 构建新种群。将所有子蛙群中青蛙个体重新混合即停车方案重新混合,生成新的停车方案种群pop,置ngen=ngen+1。 步骤8 收敛条件判定。当种群进化次数ngen<,转步骤2至步骤7;否则,终止迭代,输出最优解,即最优列车跳站运行方案。 下面以北京地铁亦庄线为例,研究列车在高峰期跳站运行停站方案。北京地铁亦庄线线路长度为23 km,共有14 座车站,亦庄火车站到宋家庄为上行方向,宋家庄到亦庄火车站为下行方向。模型中涉及运营时段为6:00~10:00,计划期(分析时段)为早高峰7:00~9:00,早高峰上行方向和下行方向的发车间隔都是3 min,模型参数Cm=1460人(m=1,2,…,M),H1=H2=2min,H3=1.5min,β1=β2=1,β3=3min/人。模型权重系数的物理含义是除了考虑乘客总等待时间和乘客总车内时间以外,再额外给最大站台人数每人一个发车间隔(3min)的时间惩罚。计划期内上行方向、下行方向各有40个车次,上行列车采用灵活跳站策略,下行列车采用全停策略。为方便计算,将计划期以Δt=30s 为单位进行时间离散化处理。客流数据取自北京地铁亦庄线刷卡数据,计划期内上行方向乘客为38 969 人,将地铁刷卡数据中乘客进站时间与乘客从闸机到站台行走时间相加得到乘客到达站台时间,将乘客进站人数按Δt时间间隔进行统计,得到计划期内乘客到达率pjif(t)(任意i,j,f,t)。计划期内客流OD 如图5 所示即需求模式1。从图5 可以看出:上行方向绝大部分客流是去宋家庄站,而其他目的地车站的客流很少;下行方向绝大部分客流是从宋家庄站到其他车站。 图5 研究周期内北京亦庄线需求模式1的客流数据 此外,为了对比研究不同需求模式下的跳站优化效果,本文还构造了一个新的客流需求模式(即需求模式2),上行方向客流也为38 969 人,计划期内客流OD 如图6 所示。与需求模式1 相比较,需求模式2中上行客流最高峰出现在次渠站和次渠南站,而需求模式1中上行客流最高峰出现在小红门站。另外,从图7 可以看出,需求模式1 中的高峰客流靠近终点站宋家庄站,但是需求模式2中的高峰客流靠近始发站亦庄火车站。特别指出虽然算例用的是动态客流OD,但是由于空间维度涉及起点、终点两个维度,难以用三维图形刻画动态客流OD,所以图5 和图6 用的都是计划期内累积客流OD 量,以区别两种需求模式下客流分布空间特征。 图6 研究周期内北京亦庄线需求模式2的客流数据 图7 目的地为宋家庄站的各站乘客人数 本模型算法实现环境为MATLAB R2020a,CPU 为AMD3900XT,12 核24 线程,内存32GB。下面分别给出需求模式1、需求模式2 下模型优化结果并进行比较分析。 对模型进行优化求解,得到需求模式1的列车运行图,如图8 所示。从图8 可以看出,在靠近亦庄火车站的前几站7:00 到7:34 发出的列车跳站较少,从7:34 到9:00 列车跳站略有增加。但是,整个计划期内列车在靠近宋家庄的最后几站跳站较多。 图8 需求模式1下亦庄线灵活跳站列车运行图 为方便分析,图9 和图10 分别给出了全停模式下亦庄线的站台人数和车内人数的统计结果。图9表明,全停模式下亦庄线站台人数高峰出现在7:30 到8:30,第一个站台人数高峰出现在同济南路站,第二个高峰出现在小红门站。图10显示,车内人数高峰出现在第6 辆车到第17 辆车。结合列车运行图,车内人数与站台人数高峰是高度耦合的。 图9 需求模式1下亦庄线全停模式各站台人数 图10 需求模式1下亦庄线全停模式各列车车内人数 图11 和图12 分别描述了跳站模式下站台人数、车内人数与全停模式下站台人数、车内人数的差值。从图11可以看出,与全停运行模式相比较,在靠近亦庄火车站前面几站的站台人数变化不大,这是因为列车在这几站跳站较少。但是,在靠近宋家庄最后几站的站台人数增加较多,尤其是小红门和旧宫站台人数增加最多,这是列车在这几站跳站较多导致的。图12 表明,靠近亦庄火车站的前面几站车内人数变化不大,这也是因为列车在亦庄火车站前面几站跳站较少。但在靠近宋家庄后面几站的车内人数变化较大,这取决于列车跳站方案、列车停靠车站的下车人数和上车人数。 图11 需求模式1下亦庄线跳站运行模式与全停模式站台人数差值图 图12 需求模式1下跳站运行模式与全停模式车内人数的差值图 图13 描述了列车跳站模式导致各OD 对客流总旅行时间的变化。具体来说,亦庄火车站前面几站上车的乘客总旅行时间大大减少,这是因为前面几站列车跳站较少乘客等待时间变化不大,但后面的列车跳站大大降低了乘客的车内时间。中间几站的乘客总旅行时间变化不大,这是因为跳站减少的乘客车内时间与增加的乘客站台等待时间相互抵销了。但是,从小红门和肖村上车的乘客旅行时间增加了,这是因为跳站对肖村上车的乘客没有任何益处,只会增加等车时间,跳站对小红门上车的乘客益处也不大。特别指出,OD 对客流总旅行时间还与客流需求有关。例如,同济南路上车到宋家庄站的乘客总旅行时间减少最多,这是因为该OD对乘客的需求最大。 图13 需求模式1下跳站模式相较于全停模式OD总旅行时间差值图 图14 是需求模式2 下优化的列车运行图。与需求模式1类似,在靠近亦庄火车站的前面几站列车跳站也较少。但是,在靠近宋家庄的后面几站列车跳站较多,这是由于需求模式2中乘客需求比需求模式1更靠近始发站。 图14 需求模式2下亦庄线灵活跳站运行模式列车运行图 从图15可看出站台人数高峰出行时段为7:30到8:50。图16 表明,车内人数高峰出现在第3 辆车到第25辆车。不同于需求模式1,乘客高峰站点为次渠南站,从次渠南站往后,第6 辆车到第30 辆车列车的满载率就达到了55%。 图15 需求模式2下亦庄线全停模式各站台人数 图16 需求模式2下亦庄线全停模式各列车车内人数 图17 中列车跳站站台人数的正负差值高峰均为荣昌东街,相较于需求模式1,需求模式2 中站台人数的波动较小。图18 表明,与需求模式1类似,跳站模式导致车内人数从次渠南开始波动,但相对于需求模式1,需求模式2 车内人数波动较小。 图17 需求模式2下亦庄线灵活跳站模式与全停模式的站台人数差值图 图18 需求模式2下亦庄线跳站模式与全停模式的车内人数差值图 从图19 可以看出,与需求模式1 类似,列车跳站模式减少了乘客总旅行时间。靠近始发站的头几站上车的乘客旅行时间减少较多。与需求模式1 不同的是,从始发站的附近站点上车的乘客人数最多,如从亦庄火车站、次渠、次渠南和经海路到宋家庄,这四个OD的乘客总旅行时间减少最多。 图19 需求模式2下灵活跳站模式相较于全停模式OD总旅行时间差值图 本文基于预测的客流OD 分布优化列车跳站方案是一个超大规模的非线性组合优化问题,优化结果以列车运行图和列车时刻表的形式呈现,列车时刻表及时向社会发布并在相当长的时间范围内不做调整。从图20 可以看出:需求模式1 下其适应度函数值进化到57 代就开始收敛,随后适应度函数值几乎保持不变;需求模式2下其适应度函数值进化到63代也开始收敛。另外,需求模式1下和需求模式2 下程序运行时间分别为4 852 s 和5 082 s。可见,本文提出的改进混合蛙跳算法有较好的收敛性能,能够满足该应用场景要求。 图20 需求模式1与需求模式2的适应度函数进化曲线 表1 给出了两种需求模式下不同列车运行模式的性能指标。具体来说,需求模式1的列车跳站模式比全停模式的乘客平均等待时间增加了2.32-1.66=0.89 min,乘客平均车内时间较少了16.40-14.20=2 min,乘客平均旅行时间减少了18.06-16.75=1.31min,乘客总旅行时间减少了1.31×38 969=51 049 min,总旅行时间减少比例为1.31/18.06=7.25%。虽然列车跳站运行增加了乘客的平均等待时间,但是最大站台人数并没有增加。另外,相较于全停模式,需求模式2下列车跳站模式导致乘客的平均等待时间增加了2.28-1.38=0.9 min,平均车内时间减少了24.34-20.66=3.68 min,平均旅行时间减少25.72-22.94=2.78 min,乘客总旅行时间减少了2.78×38 969=108 333 min,总旅行时间减少比例为2.78/25.72=10.8 %。虽然最大站台人数增加了95人,但控制在合理范围之内。可见,两种需求模式下列车跳站运行明显降低了系统的乘客总旅行时间。此外,表1还表明客流分布更靠近始发站的需求模式2 比需求模式1 更适合列车跳站运行。 表1 不同需求模式下不同列车运行模式的性能指标 表2 给出了不同需求模式下换乘乘客数量的统计结果。表2 中主动换乘是指在一定时间范围内乘客可以直达但为了减少旅行时间而采用换乘方式完成出行;被动换乘是指在一定时间范围内乘客不得不采用换乘方式完成出行。同向换乘是指乘客在中间车站换乘同向其他列车到达目的地;反向换乘是乘客多坐一站或几站,换乘反向列车达到目的地车站。从表2可以看出,列车跳站导致乘客换乘的人数并不多,需求模式1 为857 人,需求模式2 为721 人,分别占总客流需求的857/38969=2.19%,721/38969=1.85%。需求模式1下最不利的被动反向换乘占比为66/38969=0.16%,而需求模式2下没有乘客选择被动反向换乘。可见,优化后的列车跳站方案只给极少数乘客带来不便。 表2 不同需求模式下列车跳站运行换乘乘客数量统计 特别指出,在这两种需求模式下,上行方向乘客反向换乘的人数很少,对反向(下行方向)列车“全停”运行几乎没有影响。因此,本文不统计下行方向的列车运行和客流相关性能指标。 针对传统“站站停”模式难以精准匹配列车运力与乘客需求的局限性,本文以最小化乘客旅行时间和最大站台人数为目标,构建了双向轨道交通线路列车灵活跳站非线性整数规划模型,设计了改进的混合蛙跳智能算法,并通过北京地铁亦庄线的列车跳站优化验证了模型与算法的有效性。结果表明:(1)列车跳站运行明显降低了乘客的总旅行时间,并且最大站台人数也控制在合理范围之内;(2)列车跳站运行给前几站上车的乘客带来较大收益,中间站上车的乘客收益变化不大,最后一站上车的少数乘客利益受损;(3)虽然列车跳站运行导致复杂的乘客换乘行为,但是只有极少数乘客需要采用换乘方案完成出行;(4)客流需求更靠近始发站的需求模式更适合列车跳站运行。 本文研究的是列车灵活跳站优化问题,一定程度上增加了列车运行组织和乘客选择乘车方案的难度。地铁公司通过及时发布列车时刻表和列车停站信息引导乘客乘车,乘客也可以根据自己到站时间和列车时刻表来选择合适的乘车方案。本研究可进一步拓展到列车运行组织相对简单的AB 型列车跳站优化问题。另外,本文仅仅从乘客的角度优化列车跳站方案,将来可以进一步考虑列车能耗、碳排放、车辆周转率等指标,从乘客和地铁公司的角度,同时优化列车发车间隔与列车跳站方案。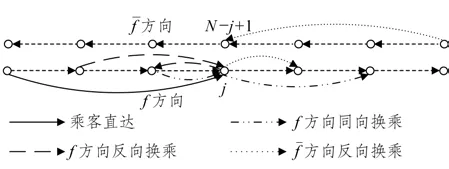
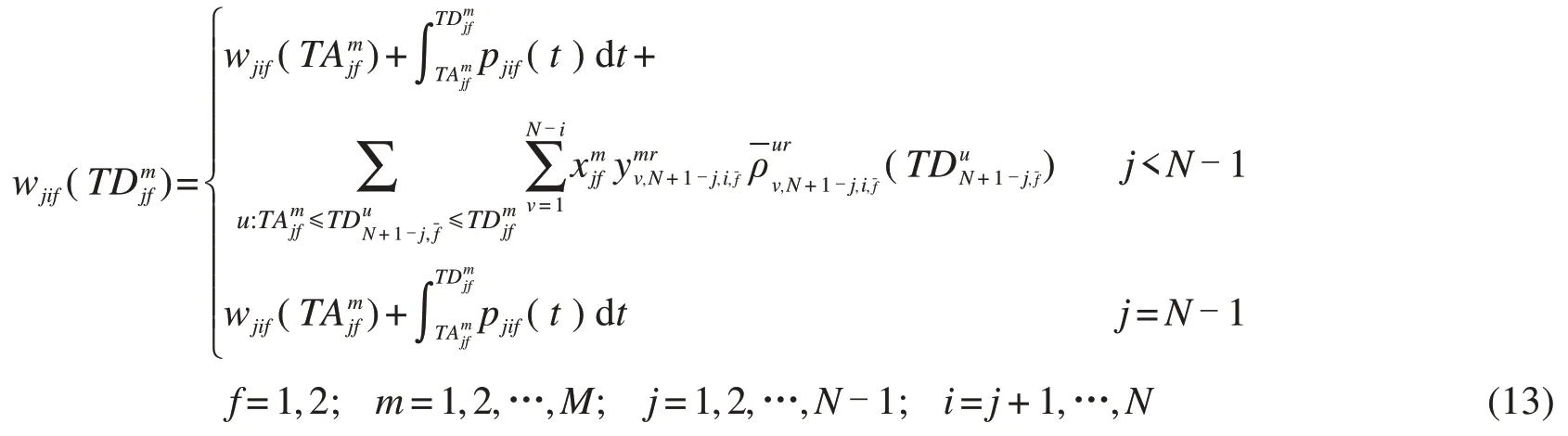


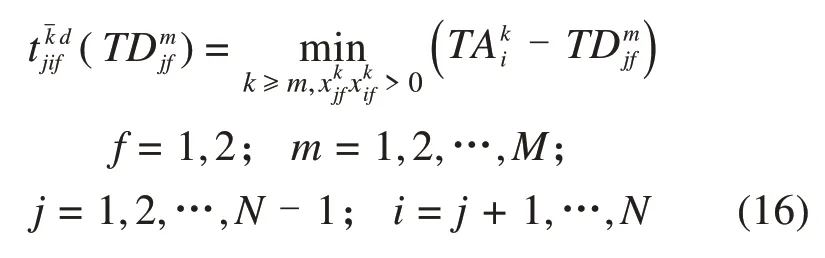






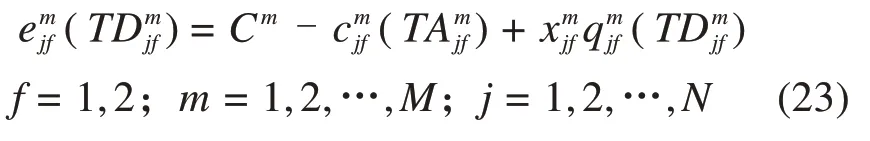







1.5 目标函数与模型构建
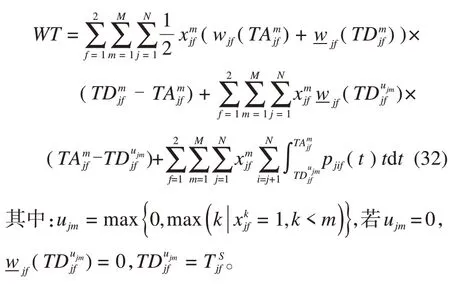



2 求解算法


3 数值算例



3.1 需求模式1




3.2 需求模式2




3.3 两种需求模式列车跳站运行性能指标分析



4 结论

