片区开发中的项目总控时序策划分析

庄国方（上海建科工程咨询有限公司， 上海 200032）

1 项目总控时序策划的内涵

1.1 项目总控的概念

近年来，我国建设工程项目呈现出信息复杂化和体量庞大化的发展形态。面对这样的趋势，传统的项目管理模式如何继续有效地为工程的建设增值，已成为现阶段需要解决的问题，项目总控模式开始受到市场的关注。

项目总控模式是在项目管理理论的基础上，结合了企业控制论和现代信息技术形成的组织模式。与传统的项目管理模式相比，项目总控一般不直接参与项目具体工作的指挥，而是在宏观和战略层面进行把控，对其他参建单位的指令仍由业主下达[1]。大型且复杂的建设项目往往具有冗杂的信息流和大量彼此制约的相邻工作面。面对这些传统项目管理模式无法解决的难点，总控团队的主要工作就是对项目实施过程中的各类信息进行整合。一方面形成通畅的信息交流，有助于提升业主与各参建单位的沟通效率，另一方面为业主的决策质量增值[2]。

1.2 项目总控时序策划的概念和特点

1.2.1 项目总控时序策划的概念

项目总控的主要任务包括时序策划、建章立制、各类管理和咨询服务等。其中，时序策划是项目总控模式应用于体量大、项目多且各项目开工进度不一的片区开发，通过收集项目间制约情况、片区内配套设施运行情况等信息后，在空间和时间上合理安排片区内的公共资源及工程实施顺序，使得片区开发总工期得到优化且开发期间内部项目互相制约的情况相对较少的一种时序管控方法[3]。作为整个片区开发的总体规划，时序策划的工作内容涉及各种管理类型和复杂工序，在很大程度上决定了片区开发期间的相邻工作面构成和资源分配情况，重要性不言而喻。

1.2.2 项目总控时序策划的特点

（1）片区整体性原则。片区开发中不能仅专注于个别项目的开发，尤其在考虑临时水电、临时道路等公共资源时要关注统筹分配，尽量减少同期开发项目间的相互制约，使片区开发建设整体增值。同时，片区本是所在城市的一部分，应考虑整体发展需求，将片区开发融入整个城市的未来发展中，顺应城市的发展趋势。

（2）适用于项目多、项目密度大的片区开发。片区开发中项目密度大，空间上互相毗邻，时间上开工进度不一，因此不仅需要考虑项目的时空关系来统筹建设顺序，还要注意合理分配片区内的公共资源，充分考虑项目间的建设逻辑关系。

（3）需考虑开发的多阶段性。片区开发初期可能存在部分公共资源不完善的情况，例如供水供电设施缺失甚至其本身就是建设项目的一部分、临时道路被划入新建规划道路范围的情况，使得相关公共资源的位置和数量在不同阶段不同项目时不一致，时序策划的结果呈多阶段性。

2 项目总控时序策划模型构建

2.1 层次分析法

片区开发具有项目多、整体性高、阶段性开发的特点，其内部有着各类主体项目、规划道路和能源管线。这些工程对于片区的各类功能有着不同的影响，使得各类项目的相互影响关系在片区开发中变得十分复杂，以致难以对其中的关键项目及项目之间的优先级关系进行识别。因此，本文采用层次分析法这一定性与定量相结合的分析方法，在决策面对定量信息较少的情况时，能够在对一个较为复杂问题内部各类影响因素的相互关系深入研究的基础上量化决策过程[5]，从而对规划道路、能源站等可作为其他项目公共资源的关键项目进行分析识别，并且结合片区的进度管理要求来确定不同项目之间的优先级，使得片区开发内部各项目的相互关系变得较为直观。

本文中的目标层是片区开发，指标层是项目主体、片区交通、片区能源等，方案层则是各类项目主体结构、各类主要交通干道和支路、各类能源站和配套管线等（如图1所示）。

图1 片区开发的层次结构模型

在片区开发层次模型中第二层各因素对第一层的影响的对比矩阵，如表1所示。

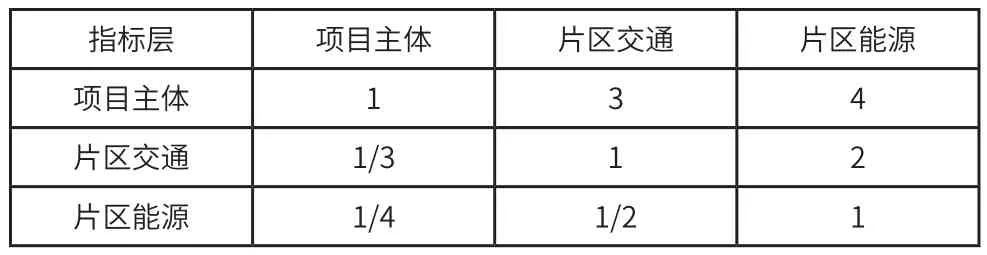
表1 片区开发的二层对比矩阵

2.2 案例分析

某城市副中心片区开发中，包括2个不同的主要项目地块、划分为2个基坑的公园（其中A基坑含能源中心）、地下环路、2条规划道路和1段需要翻修的主干路。构建层次结构模型，如图2所示。

图2 某城市副中心片区开发的层次结构模型

2.2.1 构造判断（成对比较）矩阵

在表1已知片区开发层次结构模型中第二层各因素对第一层的影响的基础上，得出层次模型中第三层各因素对第二层项目主体影响的对比矩阵（如表2所示）。

表2 片区开发的三层对比矩阵（项目主体）

层次结构模型中第三层各因素对第二层片区交通的影响的对比矩阵，如表3所示。

表3 片区开发的三层对比矩阵（片区交通）

层次结构模型中第三层各因素对第二层片区能源的影响的对比矩阵，如表4所示。

表4 片区开发的三层对比矩阵（片区能源）

2.2.2 层次单排序权值计算和一致性检验

表1所示矩阵得出：项目主体、片区交通、片区能源对片区开发影响的权向量为（0.625 0，0.238 5，0.136 5）；一致性比率CR＝CI/RI＝0.009 15/0.52＝0.017 60＜0.1。通过一致性检验。

表2所示矩阵得出：项目A、项目B、公园A坑（能）、公园B坑、地下环路、规划支二路、规划支一路、主干路翻修对片区项目主体影响的权向量为（0.280 2，0.280 2，0.152 3，0.120 8，0.056 5，0.043 1，0.043 1，0.023 7）；一致性比率CR＝CI/RI＝0.070 3/1.41＝0.049 8＜0.1。通过一致性检验。

表3所示矩阵得出：项目A、项目B、公园A坑（能）、公园B坑、地下环路、规划支二路、规划支一路、主干路翻修对片区交通影响的权向量为（0.022 2，0.022 2，0.042 4，0.042 4，0.220 6，0.162 3，0.162 3，0.325 6）；一致性比率CR＝CI/RI＝0.056 7/1.41＝0.040 2＜0.1。通过一致性检验。

表4所示矩阵得出：项目A、项目B、公园A坑（能）、公园B坑、地下环路、规划支二路、规划支一路、主干路翻修对片区能源的权向量为（0.036 7，0.036 7，0.462 4，0.036 7，0.036 7，0.091 8，0.109 0，0.190 0）；一致性比率CR＝CI/RI＝0.074 0/1.41＝0.052 5＜0.1。通过一致性检验。

2.2.3 层次总排序权值计算和一次性检验

项目A对片区开发的权值为：0.280 2×0.625 0＋0.022 2×0.238 5＋0.036 7×0.136 5＝0.185 4。

同理，可得项目B、公园A坑（能）、公园B坑、地下环路、规划支二路、规划支一路、主干路翻修对片区开发的权值，最终得出某城市副中心各项目对片区开发影响的权值比（如表5所示）。

表5 某城市副中心各项目对片区开发影响的权值比

综上所述，用层次分析法为某城市副中心片区开发的目标构建模型，通过层次总排序权值计算，将各项目的重要程度直观表现于表5中。各项目优先级排序具体如下。

（1）第一梯队：项目A、项目B、公园A坑（能）。

（2）第二梯队：公园B坑、地下环路、主干路翻修。

（3）第三梯队：规划支一路、规划支二路。

3 阶段性主要节点确定

采用层次分析法计算权重，不仅能直观地确定某城市副中心片区的建设时序优先级，还结合实际情况编制了该片区各开发阶段的主要节点。

第一阶段：项目A和项目B作为该片区中的主要项目，承担该片区的主要功能，于第一批次陆续开工。2021年8月，项目A开工；2021年12月，项目B开工。

第二阶段：公园A坑和B坑毗邻，A坑中包含了该片区内的能源站，优先级更高。应先实施A坑，同时地下环路也有部分基坑包含在A坑范围内，因此A坑和地下环路同一批次开工；B坑待A基坑出正负零后开工。2022年9月，公园A坑（能）、地下环路开工。

第三阶段：2023年9月，项目A封顶；2023年11月，公园B坑开工；2024年7月，公园A坑（能）封顶；公园A坑（能）与需要翻修的主路毗邻，因此在标高达到正负零后，主干路可以开始翻修。2024年8月，主干路翻修开工；2024年9月，项目B封顶，规划支一路与项目B毗邻，可以开工；2024年11月，项目A竣工。

第四阶段：2025年5月，主干路翻修竣工；2025年9月，公园B坑、地下环路封顶，与其毗邻的规划支二路开工。

第五阶段：2026年3月，规划支一路、规划支二路竣工；2026年4月，项目B竣工；2027年2月，公园A坑（能）、公园B坑、地下环路竣工。

4 结 语

综上所述，片区开发的时序策划较传统项目管理中的节点控制，往往需要面对项目多、项目密度大的客观情况，因此更注重开发过程中的整体性，包括片区内部的整体性以及片区所在城市的整体性，时序策划的重点不再是从单个项目进度节点控制，而是面向片区中各项目之间的工作界面交叉控制。另外，片区在开发周期中呈现出多阶段的开发模式，不同阶段中所使用的公共资源和需要重点控制的相邻工作界面也不相同。

本文以某城市副中心片区开发为例，使用层次分析法构建了分析模型；以片区开发为目标，项目主体、片区交通、片区能源为主要因素，计算了该片区内各类项目对这三种主要因素的影响权重，进一步推导出对片区开发的影响权重比，从而确定了整个片区建设的时序优先级。在此基础上，结合各项目本身的节点特殊性，策划出该片区的主要节点计划。

时序策划已经在片区开发中起到了积极的效果。为了进一步提升时序策划的合理性，在考虑各项目本身对片区开发完成后的意义的同时，还需考虑开发周期内不同阶段可能扮演的角色，因此需要将层次分析模型进一步细化，将可作为开发周期内公共资源的项目的特殊性等体现在模型中。