熔融沉积工艺参数对热塑性聚氨酯弹性体静动态力学性能的影响

雷经发，沈 强，刘 涛*，孙 虹，尹志强

（1.安徽建筑大学机械与电气工程学院，合肥 230601；2.工程机械智能制造安徽省教育厅重点实验室，合肥 230601）

0 前言

FDM技术是一种常用的增材制造技术，因其低成本、易操作、高精度等优点被广泛应用于医疗卫生、航空航天等领域[1]。FDM技术常用原料为聚对苯二甲酸乙二醇酯-1，4-环己烷二甲醇酯[2]、聚乳酸[3]、TPU[4]等高分子聚合物，其中TPU是一种（AB）n型的多嵌段共聚物，其具备较好的耐磨性、可粘接性和热可塑性，且常温下具有橡胶的高弹性[5-6]。TPU材料服役过程常承受冲击载荷作用，其受载过程的大变形应力应变行为强烈依赖于应变速率[7-8]。此外，FDM工艺参数还会对材料力学性能产生影响[9]。目前国内外学者结合多种聚合物材料如聚二甲基硅氧烷、聚乳酸等，通过正交实验、模拟仿真等手段，并采用极差分析、方差分析等方法，进行FDM工艺参数优化[10-13]；为描述热塑性弹性体在静动态载荷下的力学响应，研究者们开发并优化了落锤试验机和SHPB等能够表征材料在不同应变率下变形响应的实验装置，研究了多种热塑性弹性体在宽应变速率范围内（10-4～106）的力学性能[14-16]；基于应力应变的空间数据，构建了率相关的本构模型[17-19]并从微观角度阐述了表观形貌与力学性能的内在关联[20]。然而，目前对于FDM工艺成型的TPU材料，未能有效描述其在冲击载荷下的力学性能及率相关特性，此外FDM成型工艺参数对其力学性能的影响机制尚不明确。本文采用FDM工艺制备了多种参数组合的TPU试样，通过开展准静态和动态压缩实验，获取了应力-应变样本空间数据；以弹性模量、屈服应力为准则进行了FDM工艺参数优选，在优选参数下进一步描述了高应变率下的力学响应，最后结合ZWT本构方程构建了TPU的力学模型。

1 实验部分

1.1 主要原料

TPU，Polyflex，线材直径1.75 mm，密度1.20～1.24 g/cm3，熔融温度210℃；材料由二异氰酸酯、大分子多元醇和扩链剂组成，分子结构示意图见图1；购自苏州聚复高分子材料有限公司。

图1 TPU分子结构示意图Fig.1 Schematic diagram for molecular structure of TPU

1.2 主要设备及仪器

3D打印机，M3145K，深圳森工科技有限公司；

电子万能试验机，WDW-300A，济南方圆试验仪器有限公司；

SHPB，直径14.5 mm，洛阳利维科技有限公司；

扫描电子显微镜（SEM），Genimi SEM 500，卡尔蔡司（上海）管理有限公司。

1.3 样品制备

采用FDM设备进行TPU试样制备；其中，层间厚度为0.15 mm，平台温度为60℃，喷头温度为200、220、240 ℃，在各喷头温度下分别以10、40、70 mm·s-1的打印速率制备样品；FDM工艺原理如图2所示，通过高温喷嘴熔融并挤出线材，线材在基板平台或已加工产品上堆积、冷却、固化，逐层累积得到三维实体。

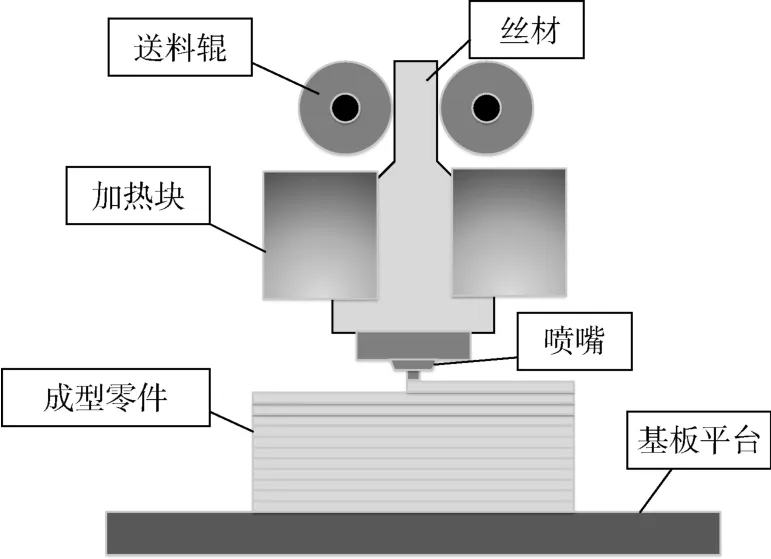
图2 FDM原理图Fig.2 Schematic diagram of FDM equipment

用于准静态和动态（高应变率）力学性能测试的试样均为圆柱状试样，按照GB/T 1041—2008，准静态试样尺寸确定为12 mm（直径）×17 mm；高应变率加载条件下，根据SHPB实验装置要求确定试样直径为12 mm，为了减小轴向和径向惯性效应，试样厚度确定为5 mm，采用邵氏硬度计测得试样硬度为95 A；图3为试样实物照片。

图3 准静态和动态试样实物照片Fig.3 Photo of quasi-static and dynamic specimens

1.4 性能测试与结构表征

准静态压缩性能测试：对试样进行单轴压缩，加载速率为1 mm/min，每次实验重复3次，取平均值，获得TPU在准静态下的工程应力-应变曲线；

动态压缩性能测试：选取杆径为14.5 mm的SHPB装置进行高应变率下力学性能测试；SHPB装置由发射装置、杆系统、测试系统和阻尼吸收装置组成（图4）；其中，发射装置为气枪；杆系统包括撞击杆（300 mm）、入射杆（1 000 mm）、透射杆（1 000 mm）和吸收杆（600 mm），杆材料为硬质实心铝杆，弹性模量为 70 GPa，密度为 2.7 g/cm3，波速约为 5 090 m/s；为降低弥散效应，在入射杆前用方形铜版纸进行整形，尺寸为10 mm×10 mm×0.6 mm（长×宽×厚），通过整形使得入射波的上升前沿变缓，减少试样应力均匀的时间，并抑制应力脉冲中的高频分量；测试系统由应变片（金属应变片获取入射信号，半导体应变片获取透射信号）、超动态应变仪和数据采集系统组成。

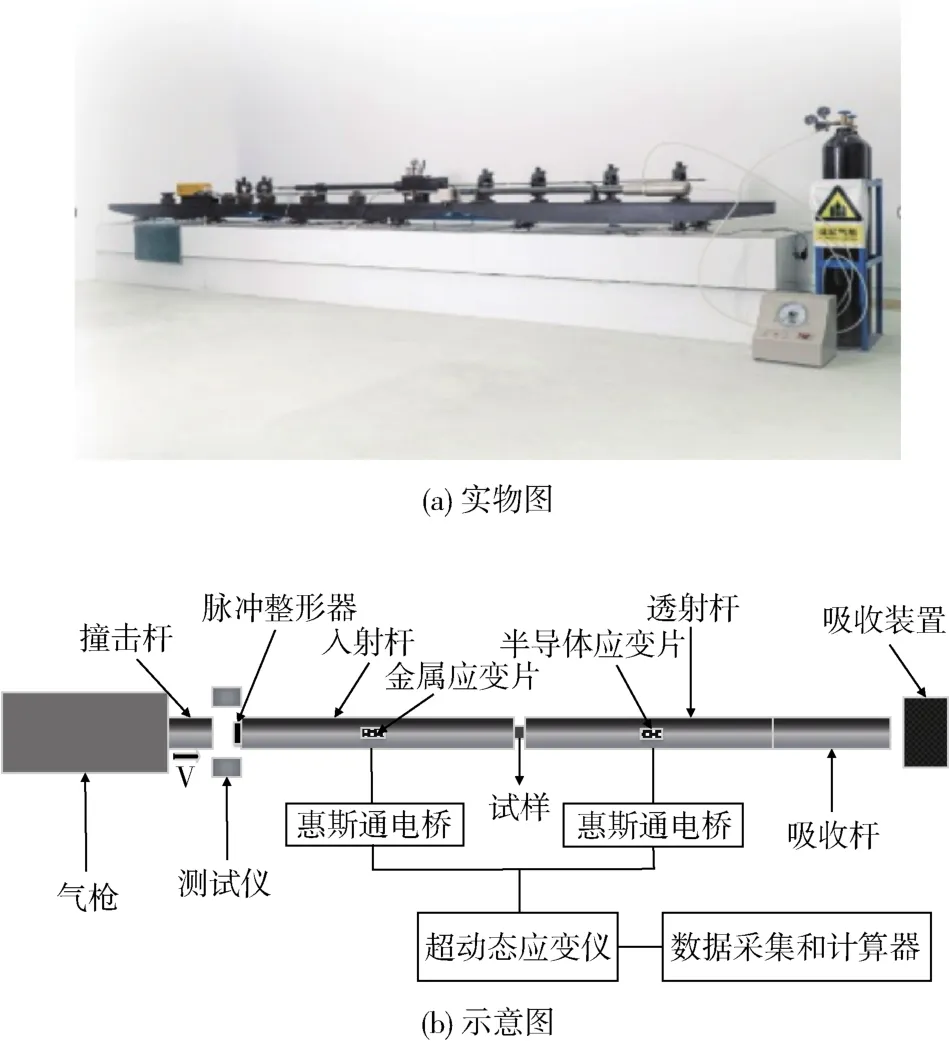
图4 SHPB装置Fig.4 Split Hopkinson pressure bar device

为获取有效数据，SHPB实验过程须满足一维应力波假定和均匀性假定；实验时将试样置于入射杆和透射杆之间，并在试样端面与杆接触区涂抹薄薄的一层凡士林以减少摩擦效应带来的误差；气枪推动撞击杆撞击入射杆，入射杆产生入射波，此时入射杆弹性应变为εi，入射波沿着入射杆传至试样，一部分应力波被弹回形成反射波，此时入射杆的反射应变为εr，另一部分透过试样传递至透射杆形成透射波，透射杆的透射应变为εt；图5（a）所示为103s-1应变率加载下采集到的原始波形信号；由图5（b）可知试样在加载时，透射波产生的应力与入射波和反射波产生的应力之和基本吻合，说明实验达到了应力平衡状态，验证了均匀性假定。

图5 TPU动态压缩原始波形及应力平衡图Fig.5 Dynamic compression raw wave form and stress balance diagram of TPU

通过调整撞击杆的撞击速度，可以得到不同的加载应变率；试样平均工程应变[ε(t)]和应力[σ(t)，MPa]的关系见式（1）：

式中ε（t）——应变率

c0——压杆弹性波速，m/s

E——压杆弹性模量，GPa

A——压杆横截面积，mm2

A0——试样面积，mm2

l0——试样长度，mm

t——加载时间，μs

微观形貌分析：采用SEM对试样微观形貌进行观察，实验前在真空环境下对试样表面进行喷金处理。

2 结果与讨论

2.1 准静态应力-应变曲线分析

选取通过3种打印速率（10、40、70 mm/s）和3种喷头温度（200、220、240℃）获取的试样的工程应力-应变曲线如图6所示。由图可见，在不同喷头温度下，打印速率为40 mm/s的试样具有更高的弹性模量。这是由于打印速率慢时，层间结合慢、温差大、层间残余应力高，导致结合力差，降低了材料的力学性能；当打印速率快时，成型过程材料供给不足导致内部产生缝隙和熔融不充分等现象，导致了材料力学性能的降低。在不同打印速率下，喷头温度220℃的试样具有更高的弹性模量。这是由于喷头温度低时，材料未完全熔融就开始进给，分子结合力差，挤出不顺畅，甚至发生挤出断裂，此时力学性能降低；而喷嘴温度高会导致材料熔融过度，发生热降解，使材料黏度下降，影响分子间的结合，同样导致材料力学性能下降。FDM工艺参数对试样弹性模量的影响如表1所示。

图6 不同打印速率和喷头温度下TPU的准静态应力-应变曲线Fig.6 Quasi-static stress-strain curves of TPU prepared at different print speed and print head temperature

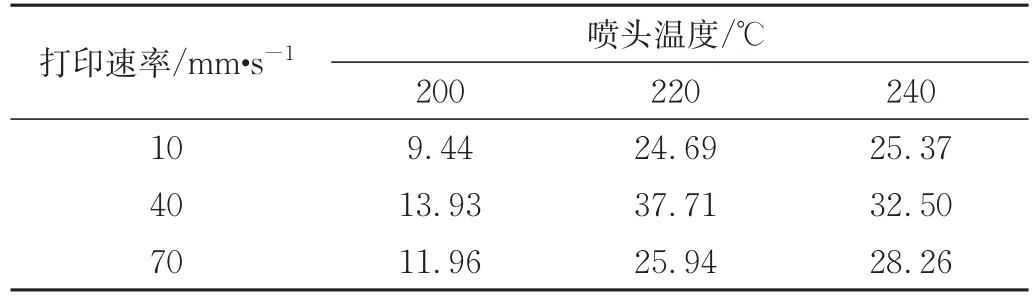
表1 FDM工艺参数对试样弹性模量的影响 GPaTab.1 Effect of FDM process parameters on modulus of elasticity of the specimens GPa

为进一步明确TPU在准静态下的应变率特性，选取通过最优参数（打印速率40 mm/s，喷头温度220℃）制备的TPU试样开展3种低应变率（0.001、0.01、0.1 s-1）加载试验，其应力-应变曲线如图7所示。由图可见，TPU在压缩载荷作用下，应力-应变曲线表现出橡胶等高聚物材料特有的“S”形非线性特征；初始阶段工程应力随着应变线性增加，随后向非线性阶段过渡；当应变量大于0.5后，工程应力显著增加，表现出一定硬化现象，且应变率越高硬化效应越明显，表现出一定应变率敏感性。这是由于准静态压缩过程中，随着应变的增大，试样层间逐步致密化，材料内部分子链间距减小、分子间作用力增强，致使软链段结晶度增加，进而表现出硬化现象。

图7 不同应变率下TPU准静态工程应力-应变曲线Fig.7 Quasi-static engineering stress-strain curves of TPU at different strain rates

2.2 动态应力-应变曲线分析

选取打印速率（10、40、70 mm/s）和喷头温度（200、220、240℃）进行动态加载，确定初始应变率为103s-1，获取试样在高应变率下的工程应力-应变曲线（图8）。由图可见，不同喷头温度下，打印速率为40 mm/s时试样具有更高的弹性模量和屈服应力；不同打印速率下，喷头温度为220℃时试样同样具有更高的弹性模量和屈服应力，表现出与准静态类似的结果。FDM工艺参数对试样弹性模量和屈服应力的影响如表2所示。

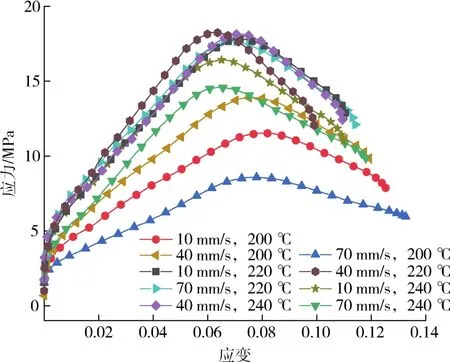
图8 不同打印速率和喷头温度下TPU的动态应力-应变曲线Fig.8 Dynamic stress-strain curves of TPU prepared at different print speed and print head temperature

表2 FDM工艺参数对试样弹性模量和屈服应力的影响Tab.2 Effect of FDM process parameters on modulus of elasticity and yield stress of the specimens

为了进一步明确动态压缩下TPU在较宽应变率范围的力学性能，选取最优参数（打印速率40 mm/s，喷头温度220℃）制备的TPU试样开展更高应变率（1 200、1 800、2 100、2 500 s-1）下的力学性能测试，应力-应变曲线如图9所示。图中可见，TPU动态压缩条件下的应变率敏感性比低应变率时更显著，且曲线也表现出高度的非线性，呈现出弹性、软化、应变硬化和卸载4个阶段；初始阶段应力与应变的比值近似为常数，为弹性阶段；随着应变增大，应力应变比值小于初始阶段，为软化阶段；随后应力随着应变的增大而急剧增大，为应变硬化阶段，应变率越大硬化效应越显著；最后阶段应力值急剧下降，为卸载阶段。这是因为高应变率载荷作用下，TPU处于绝热压缩状态，材料内部部分耗散能量转化为热能，由绝热温升引入的热软化效应使材料局部温度升高、弹性模量和黏性系数降低，进而产生软化现象；随着应变逐渐增大，材料趋于密实，分子链间距离减小，出现与准静态类似的硬化现象。

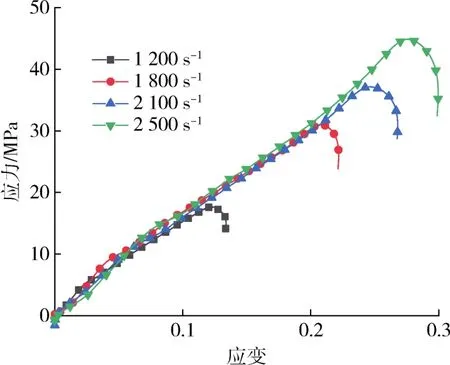
图9 不同应变率下TPU的动态工程应力-应变曲线Fig.9 Dynamic engineering stress-strain curves of TPU at different strain rates

2.3 TPU非线性黏弹性本构模型

结合上述高应变率下TPU应力-应变数据，选取ZWT本构模型对其进行拟合。ZWT模型结构示意图如图10所示，该模型由3部分构成，即1个非线性的弹簧单元和2个Maxwell单元。其本构表达式见式（2）：

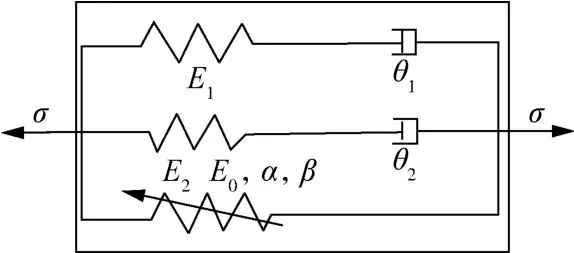
图10 ZWT模型结构示意图Fig.10 Schematic diagram of ZWT model structure

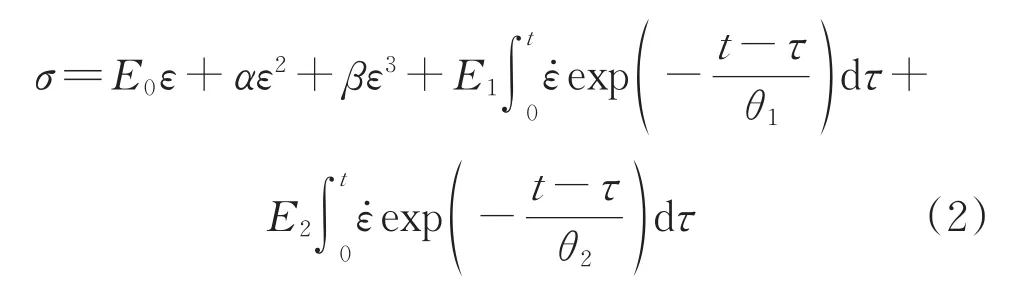
式中σ——应力，MPa

E0、α、β——非线性弹簧的弹性常数，MPa

E1——Maxwell单元的弹性常数，MPa

θ1——Maxwell单元的松弛时间，μs

E2——Maxwell单元的弹性常数，MPa

θ2——Maxwell单元的松弛时间，μs

ε——应变

τ——加载的某一时间，μs

式（2）中前3项表征材料非线性黏弹性响应，与模型中的非线性弹簧相对应；中后2个积分项分别对应材料低应变率和高应变率的黏弹性响应。当对材料开展低应变率加载时，高应变率黏弹性响应的Maxwell模型一直处于松弛状态；对材料开展高应变率加载时，低应变率黏弹性响应的Maxwell模型不能及时松弛，故Maxwell模型相当于弹簧，相应的表达式见式（3）；由于实验为恒应变率加载，故式（3）可简化为式（4）：

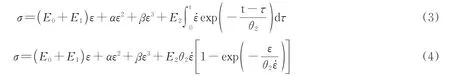
根据式（4）对实验所得应力-应变曲线进行拟合，相应参数见表3，其中R为相关系数。拟合得到的R2均高于95%。图11为拟合曲线与实验数据对比图。图中可见，拟合曲线在材料的弹性、软化、应变硬化阶段与实验曲线吻合较好，表明TPU具有显著的黏弹性特征。该模型可用于描述TPU在高应变率下的力学行为。

表3 ZWT模型拟合参数值Tab.3 ZWT model fitting parameter values

图11 ZWT模型拟合曲线与实验数据对比Fig.11 Comparison of ZWT model fitting curves and experimental data

2.4 TPU微观形貌分析

如图12所示，打印速率40 mm/s、喷头温度220℃的工艺参数下，试样孔洞、节瘤及气泡等缺陷较少。由图12（a）和（c）可见，打印速率较慢时丝材挤出量多于填充量，发生黏结融合，导致出现节瘤等缺陷；打印速率快时材料加热时间缩短，塑化程度降低，丝材存在不均匀结晶，亦会出现孔洞等缺陷。由图12（d）和（f）可见，由于喷头温度较低或较高，导致出现熔丝堆叠现象，可以清晰地观察到熔丝之间的类“楔形缝隙”；如图12（e）所示，当喷头温度为220℃时，其流动性增强，更容易通过熔丝铺覆形成“线型”熔接痕。

图12 不同打印速率和喷头温度下试样表面的SEM照片Fig.12 SEM images of surface of specimens prepared at different nozzle temperatures and printing speed

图13为最优工艺参数下试样的表面微观形貌。图中可见，表面微观结构由基体和颗粒状部分组成；基体为连续相，主要由软段构成；颗粒状部分为分散相，主要由硬段构成；大部分硬段未溶于软段之中，导致分散相较多，且相区尺寸也较大，出现“微相分离”现象，整个图呈现出“海-岛”结构；而一定尺寸的微相分离结构使得材料的结晶微区与非晶微区交叉排列，能够分散和传递外力，有效提高材料的力学性能。

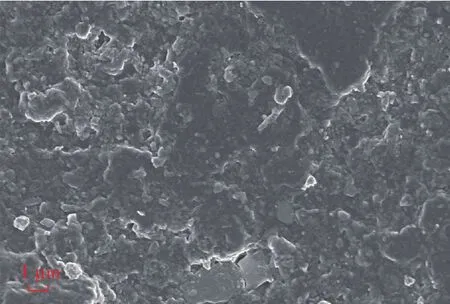
图13 优化工艺参数下试样表面的SEM照片Fig.13 SEM image of surface of specimen prepared using optimized process parameters

3 结论

（1）准静态加载下，喷头温度220℃，打印速率40mm/s下制得的试样弹性模量最高，超弹性特征显著，随着应变率增加表现出一定应变率敏感性；

（2）动态加载下，喷头温度220℃，打印速率40 mm/s下制得的试样弹性模量和屈服应力略高于使用其他工艺参数制备的试样，应变率效应显著；结合ZWT方程构建的材料的非线性黏弹性本构模型拟合误差较小；

（3）在优化工艺参数下，材料孔洞、节瘤、气泡及缝隙等缺陷较少，产生明显的“微相分离”现象。