复杂网络上随机SEIR模型的最终染病规模

刘桂荣，张刘雄

（山西大学 数学科学学院，山西 太原 030006）

0 引言

传染病一直存在于人类和社会的发展过程中，会严重危及人民的生命安全，例如SARS，COV⁃ID-19，因而研究传染病的传播规律并给出科学控制措施具有重大意义。关于传染病动力学的早期研究可以追溯到Ross针对疟疾建立的SIS模型［1］以及Kermack和McKendrick建立的SIR传染病模型［2］。此后，国内外科学工作者在传染病动力学研究方面取得了大量较好的成果［3-4］。

由于传染病的传播是通过个体间接触发生的，且个体间的接触行为具有较大的异质性，从而在复杂网络上建立传染病模型是更加合理的［5-9］。此外，传染病传播过程中，不可避免地会受到各种环境随机因素的影响，进而利用随机过程来刻画传染病的传播更符合传染病传播的实际。因此建立复杂网络上的随机传染病模型具有更现实的意义［10-11］。文献［11］建立了复杂网络上的随机SIR模型，并利用大数定律和中心极限定理分别给出了该模型最终染病规模的收敛性和分布。然而在现实中许多传染病具有潜伏期，例如流感，麻疹等［9］。有的传染病潜伏期与传染期相比并不短，不容忽视，例如艾滋病。此外，最终染病规模是一个重要的传染病传播指标。为此，本文将研究复杂网络上的随机SEIR模型的最终染病规模。

1 随机SEIR模型的建立

不考虑个体的出生和死亡，并假设人口规模为N。SEIR模型下个体的状态分别是易感者（S）、潜伏者（E）、感染者（I）或恢复者（R）。易感者被感染后变为潜伏者；潜伏期结束后，潜伏者变成感染者；感染者恢复后变为恢复者；1/υ为平均潜伏期，1/γ为感染者的病程。令K为最大度，Sk(t)，Ek(t)，Ik(t)，Rk(t)(k=1，2，…，K)分别表示t时刻度为k的易感者、潜伏者、感染者和恢复者的数量；pk(k=1，2，…，K)为网络的度分布，Nk是度为k的人数。

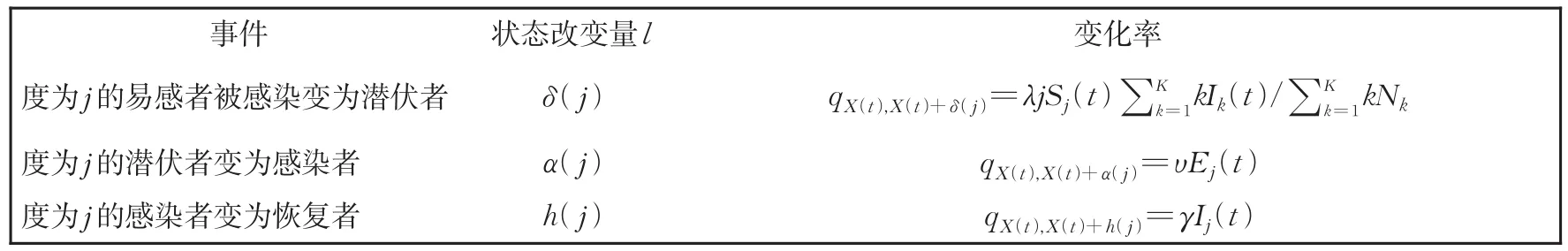
表1 随机SEIR模型的状态改变量的变化率Table 1 Change rates of state changes in the stochastic SEIR model

2 最终染病规模的收敛性

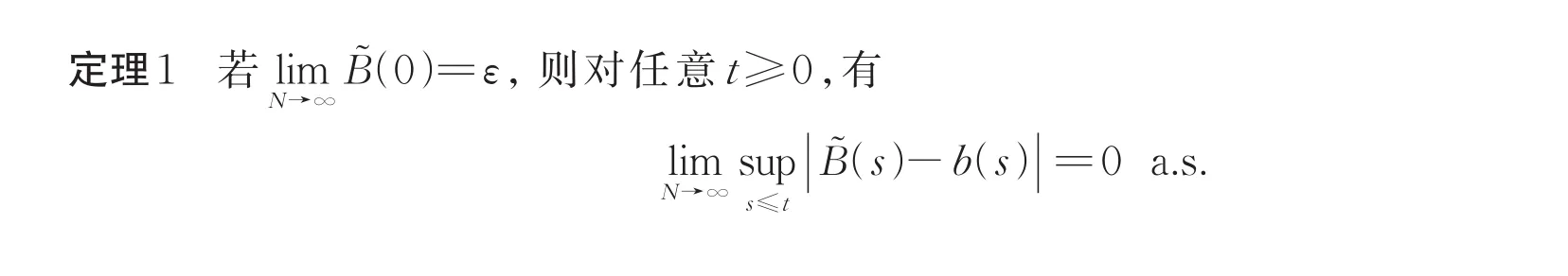
3 最终染病规模的分布

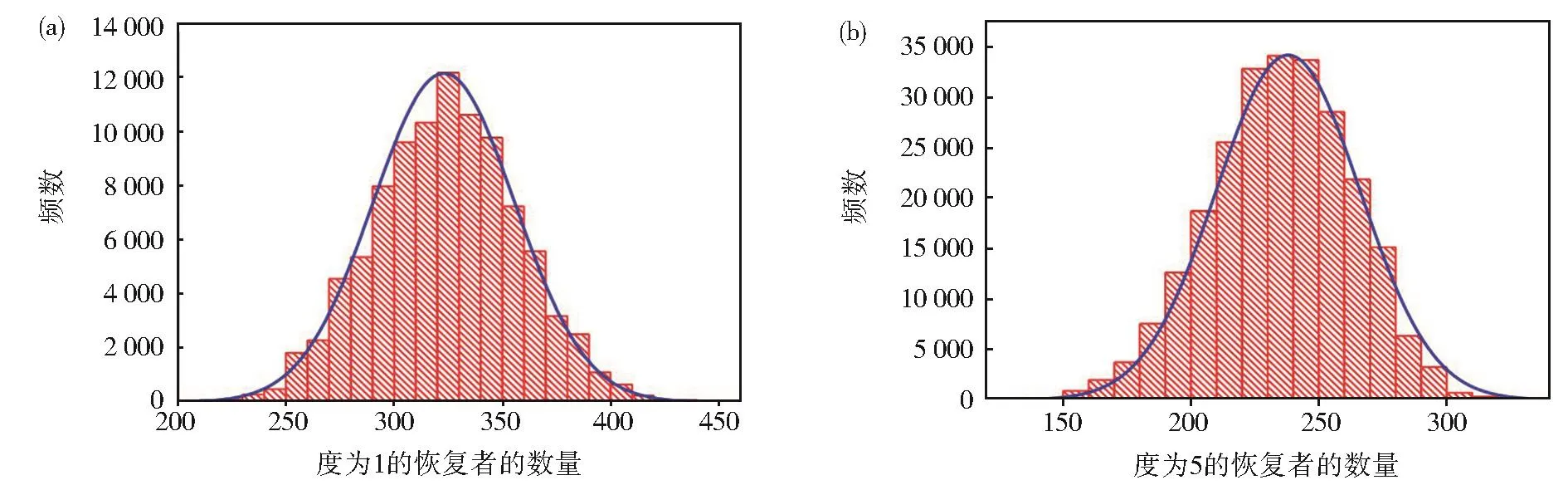
图1 （a）和（b）分别是度为1和5的最终染病规模的直方图；光滑曲线为理论结果Fig.1 (a)and(b)arethehistogramsofthefinalepidemicsizeswithdegrees1and5,respectively;Smoothcurvesarethetheoreticalresults

4 数值模拟

假设 N=5 000，K=5，λ=0.3，υ=0.7，γ=0.8，p1=0.4，p2=0.2，p3=0.2，p4=0.1，p5=0.1，S1(0)=1 900，S2(0)=950，S3(0)=980，S4(0)=485，S5(0)=490，E1(0)=50，E2(0)=25，E3(0)=10，E4(0)=5，E5(0)=5，I1(0)=50，I2(0)=25，I3(0)=10，I4(0)=10，I5(0)=5。求得传染病灭绝时间 τ=0.959 6，每个子群中染病规模密度 v1(τ)=0.064 7，v2(τ)=0.052 1，v3(τ)=0.065 4，v4(τ)=0.041 2，v5(τ)=0.047 6。 理 论 正 态 分 布 V1(τX)∼N(323.5，1 071)，V2(τ)∼N(260.5，898.5)，V3(τX)∼N(327，1 663)，V4(τX)∼N(206，635)，V5(τX)∼N(238，791.5)。 用 Gillespie 算 法 模 拟 了10 000次样本路径，得到不同度的最终染病规模的直方图，验证了理论结果的正确性。

5 结论

利用随机过程理论建立了复杂网络上随机SEIR传染病动力学模型，利用随机时间变换等方法简化了分析过程。定理2揭示了，当人口规模N→∞时，最终染病规模将依概率收敛于一个确定的随机变量。定理3给出了传染病最终染病规模的分布，进而可以给出传染病最终染病规模的均值与协方差，为传染病最终染病规模的精确预测提供理论依据。最后数值模拟验证了理论结果的合理性。从数值模拟中可以看到，度越大被感染的人数就越多。因此在防治传染病过程中可以通过隔离或其他相关政策来减少人与人之间的接触，从而更好的控制传染病的传播。本文在建立传染病模型时忽略了人口的出生和死亡，没有考虑网络度相关性、疫苗接种等因素。这些相关问题有待进一步研究。