一类具有Neumann边界条件的抛物p，m-Laplacian方程的爆破结果和整体存在性

丁俊堂，庞雯君

（山西大学 数学科学学院，山西 太原 030006）

0 引言

本文讨论了以下抛物p，m-Laplacian问题的爆破结果和整体存在性：

在问题（1）中，p>2，m>1，D是RN(N≥2)中的有界区域，∂D是D中的光滑边界，如果u 爆破，那么T*是爆破时刻，如果u整体存在，那么是一个正函数，是一个正函数且满足

当p>2，m=1时，问题（1）中的第一个方程是抛物p-Laplacian方程，当p=2，m>1时，问题（1）中的第一个方程是多孔介质方程，当p>2，m>1时，问题（1）中的第一个方程是抛物p，m-La⁃placian方程。到目前为止，已经有许多学者讨论了抛物p-Laplacian方程（见［1-15］）以及多孔介质方程（见［16-22］），然而关于抛物p，m-Laplacian方程的讨论（见［23-24］）却不是很多。本文的主要目的是研究问题（1）的爆破结果和整体存在性，主要关注了文献［4，23-24］。

在文献［24］中，Wang等主要研究了以下非线性边界条件下的抛物p，m-Laplacian问题：

其中，p>2，m>1，b≥0，u0(x)是在R+上具有紧支集的光滑函数并且满足相容性条件。通过构建一些自相似的上解和下解，文献得到了临界整体存在性指数和临界Fujita指数。

在文献［23］中，Liu等主要关注了以下非线性边界条件下的抛物p，m-Laplacian问题：

其中，p>2，m>1，b≥0，c≥0，u0(x)是在R+上具有紧支集的光滑函数并且满足相容性条件。通过构建一些自相似的辅助函数，他们推导出了上述问题非平凡解的爆破条件和整体存在性条件，获得的这些条件是由参数p，m，b，c描述的。

在文献［4］中，Ding主要讨论了以下具有Neumann边界条件和梯度源项的抛物p-Laplacian问题：

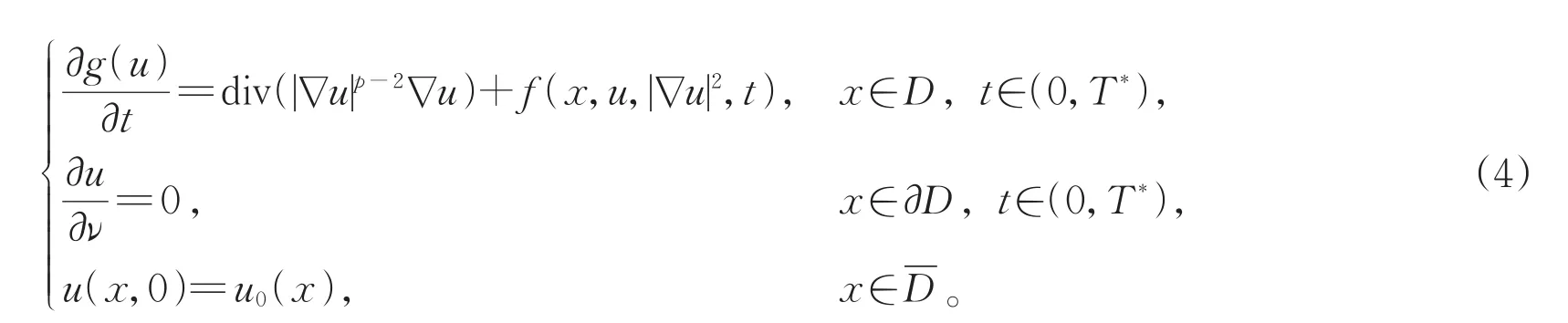
其中，p>2，D是RN(N≥2)中的有界区域，∂D是D中的光滑边界。通过构建一些合适的辅助函数，并运用微分不等式和最大值原理，得到解u在有限时刻T*爆破的充分条件。此外还给出了T*的上界以及u的爆破率的上估计。

本文使用文献［4］中的研究方法来讨论问题（1）中的爆破条件和整体存在性条件。研究发现问题（1）中的方程与问题（4）中的方程主部有所不同，所以文献［4］中的辅助函数不再适用于问题（1）。因此本文研究的难点主要在于构造新的辅助函数。

在整个研究过程中，为了方便起见，偏导数用一个逗号表示，同时还要使用求和约定，例如

1 关于爆破解的主要结论

首先我们构造如下两个辅助函数：

2 关于整体解的主要结论

3 应用