板-波传输系统的间接稳定性

王军民，郝江浩，郭雅平

（1.北京理工大学 数学与统计学院，北京 100081；2.山西大学 数学科学学院，山西 太原 030006）

0 引言

系统的稳定性是控制理论和工程中一个核心概念，是控制系统正常工作的基本前提之一。所谓稳定性，就是指系统在平衡状态下如果受到一定程度的扰动而偏离了原来的平衡状态，当扰动消失后仍然能恢复到原有平衡状态的能力。设计阻尼是系统减少扰动的理想方法。系统的稳定性依赖于阻尼区域的位置［1-2］、阻尼算子的阶数［3］、阻尼反馈的类型［4-5］和定义区域是否满足几何控制条件［6-7］等诸多因素。关于通过内部耦合的板-波系统的稳定性可见文献［8-9］，另外文献［10-11］考虑了通过边界耦合的板-波传输系统。对于通过边界耦合的板-波传输系统旨在考虑当阻尼只施加在一个子系统上，而另一个子系统上无阻尼时，整个系统是否可以达到稳定的状态。更多的板-波传输系统的工作可见［12-14］。

20世纪90年代，国际控制学者Russell引进了无穷维耦合系统的间接稳定性概念［14］。间接稳定性是指一个耦合子系统的阻尼能否通过耦合关系有效地传递到另一个子系统，从而有效地减弱整个系统的振动，实现整个系统的某种稳定性［15］。从控制的角度来看，整个耦合方程其实是由被控对象和其反馈控制器构成的闭环系统。而工业上的许多控制都是温度控制，所以热方程可以作为控制器对待。若被控对象是由波方程描述的，那么就会得到热-波方程耦合的方程。文献［7］讨论了耦合波-热方程的稳定性问题。文献［6］用热方程通过边界指数镇定了一维Euler-Bernoulli梁方程，且证明了系统的解具有Gevrey正则性。

据我们所知，由板和波所构成的耦合系统的稳定性研究主要集中于在每个子系统上都施加阻尼的情形，而只在单个子系统上施加阻尼的研究还很少。从理论上来讲，若只用单个子系统的阻尼来镇定整个耦合系统，会给无阻尼的子系统的稳定性分析带来困难。本文将对这类模型的稳定性进行研究。确切地说，在图1内，考虑如下的初边值问题

图1 板-波传输系统Fig.1 The transmission plate-wave systems

因而系统（1）的能量关于时间t非增。并且等式（3）表明系统（1）的耗散项仅产生于板的部分，而与波的部分无关。

本文结构如下：第1节给出预备知识；第2节证明系统（1）的适定性；第3节建立系统（1）的多项式稳定性；第4节总结内容，得出结论。

1 预备知识

为了研究系统的能量衰减性质，我们先引入函数空间

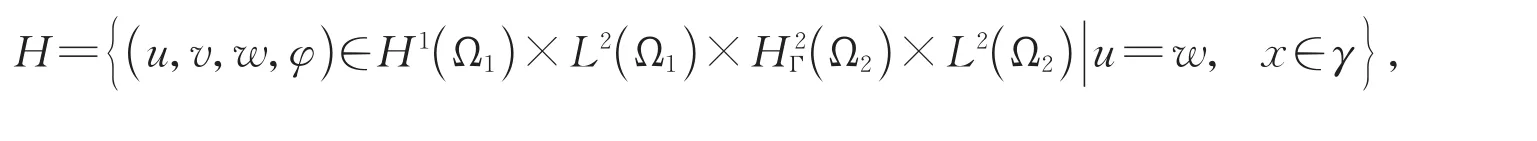
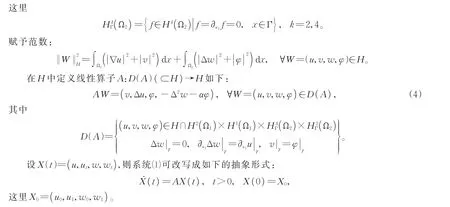
2 适定性

本节我们先给出系统（1）的适定性。

3 稳定性

4 结论

在传输系统（1）中，板和波的能量只通过边界来交互传递，而阻尼只施加在板方程上，这样会给无阻尼的波能量的估计带来困难。用频域分析法和能量乘子法导出的能量传递等价关系式（24），是传输系统（1）的能量是否被估计的关键因素。为了估计（24）右端的边界积分项，必须使用板的高阶能量，故我们只能得到其解的能量的多项式衰减率。在这种情况下，系统（1）的非指数稳定性和多项式能量衰减率的最佳估计仍是一个未解决的问题。