基于损伤力学的碟盘刀具振动截割煤岩径向载荷

刘春生， 程 硕， 李鑫鹏

(黑龙江科技大学 机械工程学院， 哈尔滨 150022)

0 引 言

截割刀具是采掘机械工作机构的核心要素，刀具截割煤岩的载荷谱反映其综合性能，对机构的研制具有重要的意义。国内外学者对岩石破碎理论模型进行了诸多研究，Krajcinovic等[1]结合断裂力学和统计强度理论，建立了脆性材料的损伤力学本构模型。Huang等[2]基于损伤演化理论与动态裂纹扩展，建立了岩石单轴压缩损伤模型。Salari等[3]考虑了岩石的拉伸损伤性质，建立了岩石弹塑性三轴本构模型。Shao等[4]构建了一种脆性岩石各向异性损伤和蠕变本构模型。许江等[5]假设岩石服从Drucker-Prager准则，基于Weibull分布建立了岩石的损伤本构模型。李德根等[6]构建了无齿碟盘刀具复合截割煤岩的损伤力学模型。李树春等[7]引入岩石应力应变全过程特征参量，基于连续损伤理论和统计强度理论，建立了岩石损伤本构模型。张德等[8]基于Weibull分布和Mohr-Coulomb屈服准则，建立了冻土损伤本构模型。陈松等[9]考虑岩石节理几何特征，建立了断续节理岩体复合损伤本构模型。汪杰等[10]引入岩体结构效应与载荷耦合作用，建立了节理岩体损伤演化模型及损伤本构模型。张超等[11]基于Weibull分布建立了应变软化类岩石统计损伤本构模型，并对模型进行修正，对岩石各阶段变形特征进行描述。袁小平等[12]采用体积应变表示岩石损伤变量的演化，建立了岩石弹塑性损伤本构模型。蒋浩鹏等[13]，引入热损伤变量，建立了高温岩石Weibull分布统计损伤本构模型。刘春生等[14-16]基于碟盘刀具振动截割煤岩的数值模拟与实验，建立了碟盘刀具截割煤岩的力学模型，探究碟盘刀具振动截割煤岩的载荷特性。

笔者基于煤岩的损伤力学，建立碟盘刀具振动截割煤岩的径向载荷损伤力学模型，对比分析数值模拟和实验的载荷峰值均值，验证力学模型，利用载荷谱的峰值标准差和幅频特性分析煤岩的崩落状态，给出载荷特性，为碟盘刀具截割机构的研制提供理论依据。

1 煤岩损伤变量

碟盘刀具是一种以轴向振动和径向进给的复合运动形式截割煤岩的刀具，其边缘均匀分布50个牙齿。碟盘刀具的楔面角度为α，半径为R，轴向振动速度为vz，径向进给速度为vj，截割煤岩的厚度为h，煤岩的崩落角为ψ，如图1所示。

碟盘刀具的轴向振动为简谐振动，其振动方程为s=Asin(ωt)，s为振动位移量，A为振幅，ω为振动频率，t为时间。

1.1 损伤本构关系

由Lemaitre提出的应变等价性原理，可得煤岩损伤本构关系为[7]

(1)

式中:σ0——煤岩有效应力，MPa；

E——弹性模量，MPa；

ε——应变；

D——损伤变量。

煤岩力学性质具有复杂性和随机性，若将煤岩离散，视其由无数个微元体组成，假定煤岩微元强度服从Weibull分布函数，其概率密度函数为

式中:W——微元强度的随机分布变量；

m、W0——Weibull分布参数。

碟盘刀具对煤岩损伤程度大小可以通过损伤变量进行表征，根据式(1)可得煤岩达到破碎时，其损伤变量为

(2)

煤岩破碎的过程，实质是损伤发展与累积的过程。损伤变量能够反映煤岩微元体破坏概率，则煤岩损伤可视为微元体破坏的累积效应，可得：

(3)

1.2 损伤变量

碟盘刀具无振动截割煤岩时，仅存在径向进给运动，其产生的损伤变量为D1。碟盘刀具振动截割煤岩时，煤岩的损伤是由刀具复合运动产生的，煤岩的损伤变量，在无振动截割煤岩的基础上，考虑轴向振动的影响因素，为计算方便可将振动时与无振动时径向进给运动的截割比能耗比值作为振动损伤系数K，在特定频率下，煤岩损伤与振动频率和振幅成正比，文中在特定频率下计算损伤系数。

借鉴镐型齿截割比能耗公式[17]，给出刀具径向进给运动的截割比能耗公式为

式中:HW——截割比能耗，kW·h/m3;

Fj(t)——刀具径向载荷，kN;

V——被截割煤岩体积，m3。

两种截割工况下径向进给速度与被截割煤岩体积均相同，则可得：

(4)

式中:HW1——碟盘刀具无振动时径向进给运动截割煤岩的比能耗，kW·h/m3；

HW2——碟盘刀具振动时径向进给运动截割煤岩的比能耗，kW·h/m3;

Fj1(t)——碟盘刀具无振动时径向载荷，kN;

Fj2(t)——碟盘刀具振动时径向载荷，kN;

V1——碟盘刀具无振动截割煤岩体积，m3;

V2——碟盘刀具振动截割煤岩体积，m3;

D2——碟盘刀具振动时径向进给运动截割煤岩造成的损伤变量。

采用梯形数值积分计算振动损伤系数K，以载荷谱两相邻时间数据点的差为间隔，将载荷谱区域分为N个梯形，两相邻载荷数据值作为梯形上下底长、时间间隔为高，计算梯形面积，对其累加，可得载荷谱的积分值，其原理公式为

2 径向载荷损伤力学模型

碟盘刀具振动截割煤岩过程中，煤岩破碎前受到挤压力的作用，在局部产生粉碎并形成密实核，进而破碎煤岩，由图1可见，碟盘刀是截割煤岩过程中仅有1/2为有效截割面积，如图1所示。

2.1 牙齿载荷力学模型

煤岩的强度服从Mohr-Coulomb强度准则，煤岩是沿着某一个不确定的破裂面发生剪切破坏。碟盘刀具截割煤岩时，煤岩的破碎服从Mohr-Coulomb强度准则，即剪切破裂面上的剪应力达到或超过由正应力引起的内摩擦力和煤岩本身的抗剪强度(黏聚力)之和为

τm≥c+σmtanφ，

式中:τm——煤岩任意平面上的剪应力，MPa；

σm——煤岩任意平面上的正应力，MPa;

c——煤岩的黏聚力，MPa；

φ——煤岩的内摩擦角，(°)。

以碟盘刀具有效截割部分对称线处的牙齿C为例，位置如图1所示。对其受力分析，如图2所示，在煤岩的剪切破坏线方向上存在破坏煤岩的力FS和抵抗煤岩破坏的力FR。

图2 牙齿C与煤岩作用的受力Fig. 2 Force of interaction between tooth C and coal rock

(5)

(6)

FH=FS-FR,

(7)

式中:σ——剪切破坏线上的有效正应力，MPa；

τ——剪切破坏线上的有效剪切应力，MPa；

μ——摩擦系数；

l——剪切破坏线长度，l=h/sinψ，mm；

ψ——崩落角，(°)；

b——牙齿C接触宽度，b取15.70，mm。

煤岩的破碎遵循Mohr-Coulomb强度准则，根据其主应力公式可得:

(8)

式中:σ1——第一主应力，MPa；

σ3——第三主应力，MPa。

结合(1)、(4)、(8)得：

(9)

将式(5)、(6)、(9)代入式(7)，令σ3=0，可得牙齿C在剪切破坏线方向受到的力为

c}bdx。

(10)

式中:σ*——剪切破坏线上的正应力，MPa；

τ*——剪切破坏线上的剪切应力，MPa。

由图2可知，牙齿C截割煤岩时受到的合力F与FH的关系为

(11)

式中，ξ——牙齿C受到的合力与剪切破坏线的夹角，ξ=90°-α-ψ，(°)。

结合式(10)、(11)，可得F为

由图2可知，当vz≠0，vj>0时，即碟盘刀具振动截割煤岩时，牙齿C在水平方向受到的力为

(12)

式中，γ——水平面与牙齿C受到的合力的夹角，γ=ψ+ξ，(°)。

2.2 Weibull分布参数

依据煤岩的单轴抗压实验所得的数据，求取力学模型中的Weibull分布参数m、W0。

结合式(2)、(3)，可得：

(13)

对式(13)两侧同时取两次对数，化简可得：

对煤岩进行单轴抗压实验，可得煤岩的各项参数，依据实验应力及应变数据点可计算出X和Y序列，对其进行线性回归分析，可得参数m和W0的值，如表1所示。

表1 煤岩的参数Table 1 Parameters of coalstone

2.3 碟盘刀具载荷力学模型

碟盘刀具振动截割煤岩时，煤岩呈月牙状破碎，其应力延伸扩展变化也为月牙状，应力面积从中间向两侧逐渐递减。

依据碟盘刀具应力分布规律和牙齿均匀分布的特点，碟盘刀具有效截割部位的牙齿受力由牙齿C处沿碟盘刀具边缘向两侧递减，则由牙齿C径向载荷损伤力学模型式(12)推导得碟盘刀具力学模型为

(14)

式中，θ——相邻牙齿间夹角，θ取7.2，(°)。

3 数值模拟与实验

3.1 截割煤岩数值模拟

采用ABAQUS软件，建立碟盘刀具和煤岩三维模型，对模型进行网格划分，如图3所示。将碟盘刀具模型设置为刚体，其尺寸分别为：刀具半径R=125 mm，牙齿尖端等效半径r=3 mm，楔面角度α=55°。煤岩体的长宽高分别为350、250和100 mm，抗压强度σc=19 MPa。

图3 有限元模型Fig. 3 Finite element model

煤岩截割厚度分别取10、15、20和25 mm，碟盘刀具运动参数设定振动频率f=45 Hz、振幅A=2 mm、径向进给速度vj=300 mm/s，数值模拟碟盘刀具振动截割煤岩的过程，得径向载荷谱如图4所示。

图4 径向载荷谱数值模拟Fig. 4 Numerical simulation of radial load spectrum

由图4可知，碟盘刀具径向载荷随截割煤岩厚度的增加逐渐增大。碟盘刀具切入煤岩，载荷谱呈逐渐上升趋势，碟盘刀具稳定截割煤岩阶段，载荷谱呈现周期性波动。

3.2 截割煤岩实验

碟盘刀具振动截割实验台由破岩系统和检测系统构成[16]。设定碟盘刀具运动参数：振动频率f=45 Hz、径向进给速度vj=300 mm/s，煤岩抗压强度σc=19 MPa，截割厚度分别取10、15、20和25 mm，利用实验台进行碟盘刀具振动截割煤岩实验，获得径向载荷谱，如图5所示。

图5 实验径向载荷谱Fig. 5 Radial load spectrum of experiment

将载荷谱分为Ⅰ、Ⅱ、Ⅲ三个区域：碟盘刀具切入煤岩阶段，载荷谱呈上升趋势，为Ⅰ区；碟盘刀具稳定截割阶段，载荷谱呈较规律波动状态，为Ⅱ区；碟盘刀具切出煤岩阶段，载荷谱呈下降趋势，为Ⅲ区。由碟盘刀具稳定截割阶段载荷谱可知，实验中碟盘刀具截割煤岩的径向载荷大小与截割厚度的呈正相关。

4 模型验证与载荷特性

4.1 模型验证

结合式(4)计算振动损伤系数K，为避免碟盘刀具切入、切出煤岩阶段载荷不稳定的影响，选取振动(图5 b)与无振动(运动参数vj=300 mm/s、h=15 mm)径向载荷谱的Ⅱ区作为分析处理区段，见图6。

图6 振动与无振动径向载荷谱Fig. 6 Vibration and non-vibration radial load spectra

将图6径向载荷谱的数据点代入式(4)，取其平均值，得振动损伤系数K=0.49。表1中Weibull分布参数与振动损伤系数K代入式(14)，可得截割厚度10、15、20和25 mm的碟盘刀具径向载荷。将数值模拟和实验的的径向载荷峰值均值与理论值对比分析，如表2所示。

表2 径向载荷对比Table 2 Radial load comparison

根据表2得，截割厚度为10、15、20和25 mm，理论值与数值模拟的径向载荷峰值均值的误差分别为3.39%、2.39%、2.43%、4.46%，与实验的误差为13.13%、15.25%、2.08%、0.18%，故截割厚度为10～25 mm，理论值与数值模拟和实验的径向载荷峰值均值的平均误差分别为3.17%、7.66%，验证了碟盘刀具径向载荷损伤力学模型准确性。

4.2 载荷特性

将表2中数据点在图中绘出，并将实验数据点进行拟合，如图7所示。

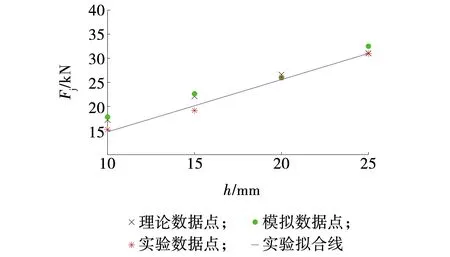
图7 理论、模拟与实验径向载荷Fig. 7 Theoretical, simulated and experimental radial loads

实验拟合方程为Fj=1.085h+3.88，由图7可知，理论、数值模拟和实验数据点均分布在拟合线两侧，碟盘刀具振动截割煤岩径向载荷与截割厚度呈线性正相关。

碟盘刀具振动截割过程中，煤岩具有崩落现象，载荷谱中呈现波动状态，载荷谱的波动幅度、波动频率可表征煤岩的崩落状态。

载荷谱波动幅度可以体现煤岩崩落块度的大小，其可由载荷谱的波峰值与均值拟合线的离散程度(即标准差)表征。选取图5实验载荷谱Ⅱ区，计算载荷谱波动的均值为

(15)

式中:Fjmax i——第i个波峰载荷，i=1，2，…,n，kN；

Fjmin i——第i波谷载荷，kN。

根据式(15)求取载荷谱的波动均值，对截割厚度为10、15、20和25 mm的载荷谱均值进行拟合。给出载荷谱的峰值标准差公式为

(16)

依据式(16)，计算求得截割厚度为10、15、20和25 mm时，峰值标准差分别为1.94、2.90、7.65、11.07，由此数据(拟合)可得其随截割厚度近似呈指数(S=0.695 3e0.111 9h)规律变化。

通过载荷谱幅频特性分析煤岩崩落的状态，采用傅里叶变换对图5的载荷谱Ⅱ区进行频谱分析，其幅频特性如图8所示。将不同截割厚度下幅频特性曲线的幅值除以其零频幅值，其不同频段载荷幅值相对占比，如图8 b所示。

图8 径向载荷幅频特性 Fig. 8 Amplitude-frequency characteristics of radial load

由图8可知，截割厚度为10、15、20和25 mm载荷谱的波动频率主要集中在6.6～8.3、1.6～9.3、1.3～4.3、0.66～2.3 Hz，随截割厚度增加，低频成分相对占比逐渐增大，中高频成分相对占比逐渐减小。

5 结 论

(1)基于煤岩微元强度的随机统计分布规律和振动损伤系数，给出了振动截割煤岩时径向进给运动造成的损伤变量，根据Mohr-Coulomb强度准则，结合碟盘刀具应力分布规律和牙齿均匀分布特点，建立了碟盘刀具振动截割煤岩的径向载荷损伤力学模型。

(2)运用数值模拟和实验方法研究了不同截割厚度下碟盘刀具振动截割煤岩的特性，截割厚度为10～25 mm时，数值模拟和实验的载荷峰值均值与理论值的平均误差分别为3.17%和7.66%，验证了所构建力学模型的准确性。

(3)采用数理统计和频谱方法分析了截割厚度为10～25 mm的载荷谱，随截割煤岩厚度的增加径向载荷呈线性增大趋势，峰值标准差随截割厚度近似呈现指数规律变化，载荷谱频率中幅值低频成分相对占比逐渐增大，表征煤岩大块崩落的概率及块度逐渐增大特征。