倾倒变形边坡板岩蠕变的力学特性

姚彦欣， 欧荣轩， 谭维佳

(1.清远职业技术学院 机电与汽车工程学院， 广东 清远 511510； 2.清远市水利水电勘测设计院有限公司，广东 清远 511510； 3.长安大学 地质工程与测绘学院， 西安 710054)

0 引 言

层状地层在我国西南地区大量孕育，其中倾倒变形在层状边坡中是较常见的变形破坏类型[1-2]。研究表明，倾倒变形边坡在演化过程中时效变形明显，蠕变现象显著[3-4]，由此，针对倾倒变形边坡岩石开展蠕变实验具有十分重要的价值。目前，已有较多岩石蠕变特性方面的研究，但针对倾倒变形边坡岩石的研究较少。蒋海飞等[5]开展高应力作用下砂岩蠕变实验，发现孔隙水压增强了砂岩的变形能力，修正广义Kelvin模型。秦哲等[6]以露天矿坑边坡花岗质碎裂岩为研究对象，指出随着饱水-失水循环次数的增加，瞬时弹性应变和蠕变应变均递增，蠕变速率随之增高。左清军等[7]开展了富水板岩三轴压缩蠕变实验，分析水对蠕变变形的影响，建立考虑含水率的蠕变本构模型。张峰瑞等[8]研究化学腐蚀-冻融综合作用下的石英岩和石英砂岩蠕变特性，分析冻融循环次数和化学腐蚀作用对蠕变变形、长期强度的影响。王青元等[9]针对煤层顶板绿砂岩，得到岩石在不同冲击荷载作用下的蠕变规律。

笔者以云南某水电工程近坝库岸倾倒变形边坡为研究背景，开展板岩在不同围压条件下的三轴压缩蠕变实验。

1 蠕变实验

1.1 实验材料及方案

文中研究背景为云南某水电工程近坝库岸倾倒变形边坡，该边坡在倾倒变形演化过程中时效变形明显，取新鲜板岩，在实验室加工成直径50 mm、高100 mm的圆柱体试样，两端打磨平滑，板岩基本物理力学参数如表1所示。

表1 基本物理力学参数Table 1 Basic physical and mechanical parameters

实验仪器采用RLW-2000型岩石三轴流变仪，进行三轴压缩蠕变实验，围压σ3设置为10、20和30 MPa，采取逐级增量加载的方式，每一级加载历时约500 h，每级加载应力Δq=Kqf/n，其中，K为强度降低系数，通常取0.65～0.85，qf为破坏偏应力，n为加载级数[10]。在蠕变实验前，先开展常规三轴压缩实验，板岩蠕变实验加载方案如表2所示。应力路径如图1所示，以围压10 MPa为例。

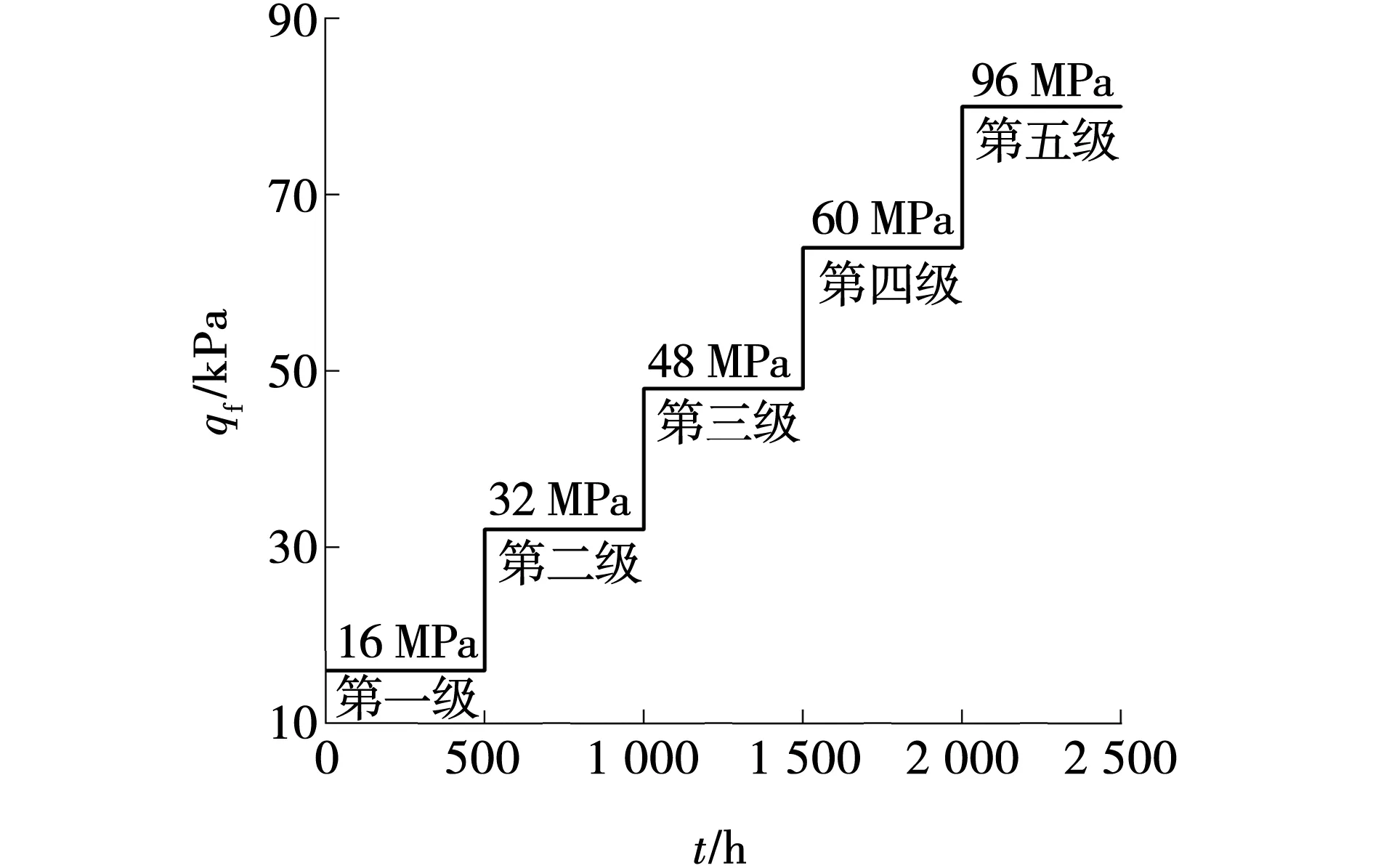
图1 应力路径Fig. 1 Stress path

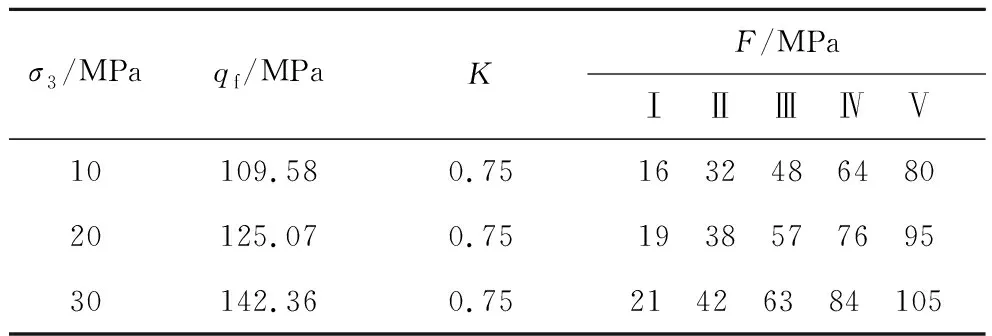
表2 实验加载方案Table 2 Test loading scheme

1.2 实验结果

通过蠕变实验得到逐级加载蠕变实验曲线，将各级偏应力标识于曲线上，以围压10 MPa为例，如图2所示。对图2进行玻尔兹曼叠加处理[10]，得到分别加载蠕变曲线，如图3所示。以图3中0～490 h的蠕变数据为基础，每隔70 h采集偏应力和轴向应变数据，其中，0 h时刻点为趋近于0 h的数据，绘制等时偏应力-应变曲线，如图4所示。

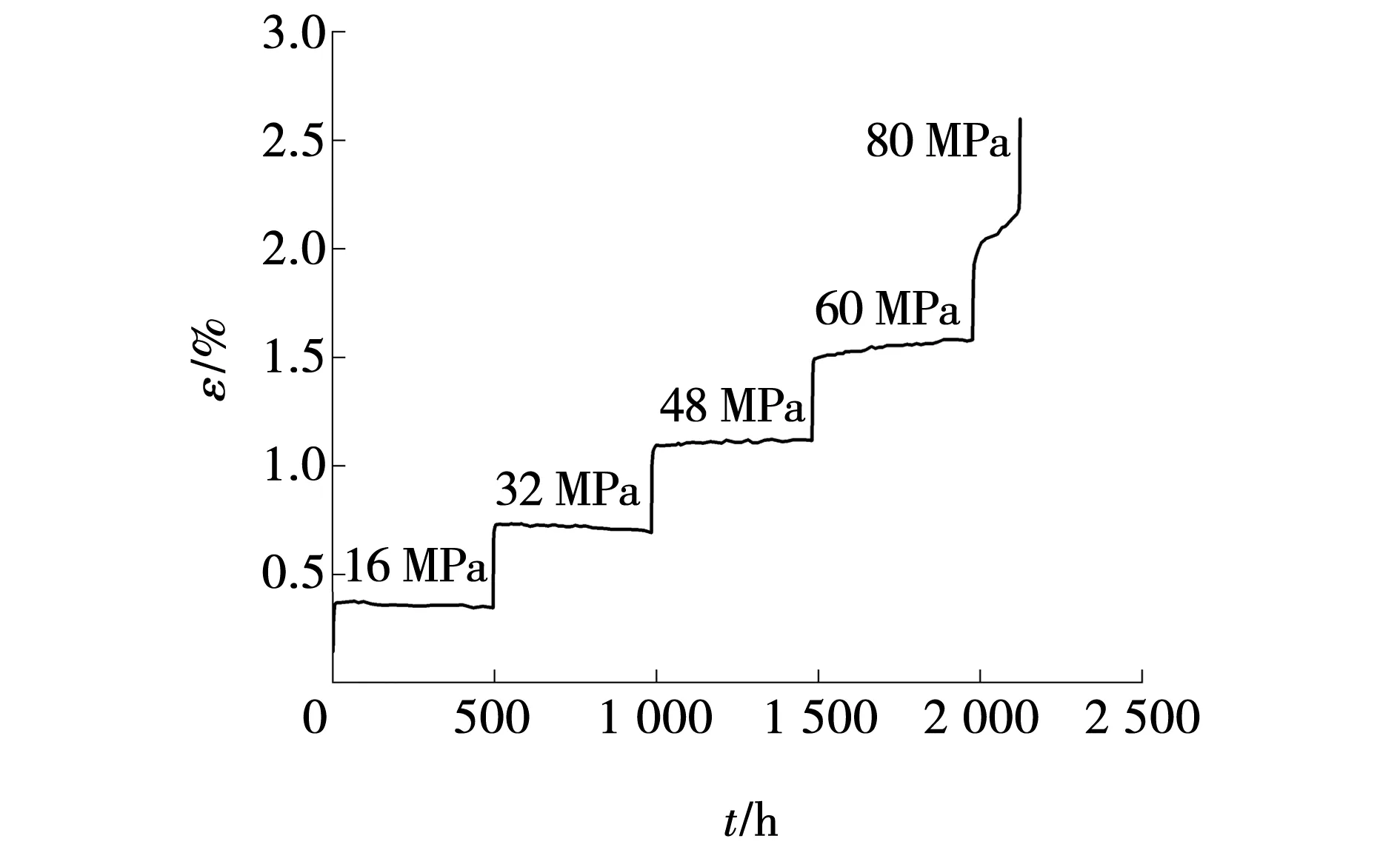
图2 逐级加载蠕变曲线Fig. 2 Progressive loading creep curves

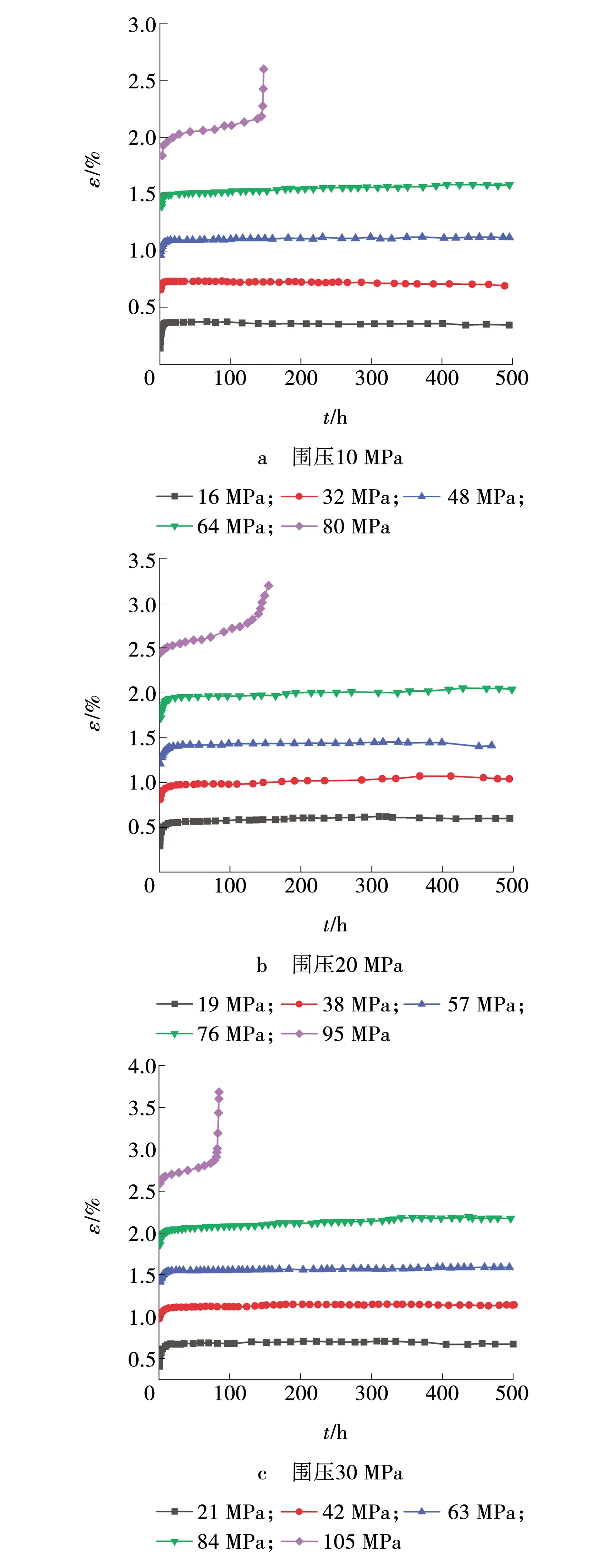
图3 分别加载蠕变曲线Fig. 3 Separately loaded creep curves

图4 等时偏应力-应变曲线Fig. 4 Isochronous deviatoric stress-strain curves

由图1、2可以看出，偏应力荷载逐级增加，每一级加载历时约500 h，在每一级加载期间，岩石轴向应变逐渐累积，前四级仅发生衰减和稳定蠕变行为，最后一级加载下还发生了加速蠕变行为，随即岩石屈服破坏。

由图3可以看出，板岩在每一级的加载作用下，首先产生瞬时弹性变形，该过程瞬间发生，接着岩石进入轴向应变率递减的衰减蠕变阶段，经历10～30 h后轴向应变率趋于稳定，此时岩石进入稳定蠕变阶段，最后一级加载下岩石进入了加速蠕变阶段，该阶段历时短，轴向蠕变应变剧增。

由图4可以看出，等时偏应力-应变曲线由两部分组成，左侧部分为0 h数据段，表现为线性相关，右侧部分为70～490 h数据曲线簇，在前三级加载下线性相关，后两级加载下非线性特征明显，曲线簇表现出逐渐偏于应变轴的趋势，通过对等时偏应力-应变曲线取拐点[11]的方法，确定三种围压下的板岩长期强度分别为58.8、72.3和78.6 MPa，长期强度随着围压的增大而递增。

2 板岩非线性蠕变力学模型

板岩在荷载作用下，对每一级加载瞬间的响应是弹性的，接着随着时间推移，衰减和稳定蠕变阶段中表现有黏弹性和黏塑性行为，根据统一流变力学模型理论[12]，选择Maxwell模型作为基础模型，该模型包含Hooke体、Newton体，模型示意如图5所示。

图5 Maxwell模型示意Fig. 5 Schematic of Maxwell model

由图5可见，Hooke体可描述岩石瞬时弹性变形，Newton体通常可用于描述黏弹性变形，由于文中板岩蠕变的非线性特征十分明显，而Newton体是常规线性体，故对Newton体进行非定常化，引入文献[13]中非定常黏滞系数为

(1)

式中：σ2——Newton体的应力；

η0、λ、c——与蠕变程度相关的参数；

ε2——Newton体的应变。

当板岩应力水平超过长期强度时，岩石蠕变的非线性特征愈发显著，表现为黏塑性变形，此时还应有黏塑性元件，文中引入黏塑性元件的本构方程为

(2)

为了响应政府号召、补充现有研究、拓展上海环城绿带的复合功能,本文对上海环城绿带百米林带植物群落进行了全面的调查研究。从群落外貌特征、景观结构、空间特征以及游憩利用现状4个方面对百米林带中101个典型植物群落样方进行调查,明确上海环城绿带百米林带植物群落结构特征以及布局模式,针对现状存在的问题，分析其可能产生的原因,并提出优化建议; 同时通过现场观察及问卷调查，对上海环城绿带百米林带植物群落的游憩现状进行分析和总结,思考在维持林带生态景观功能的前提下,提升游憩功能的适宜性。以期对上海环城绿带百米林带后续建设及优化改造提供指导性建议,使其能更好地满足城市生态建设及游憩服务的需求。

η3——黏滞系数；

σ——每一级偏应力；

σS——长期强度。

将Maxwell非定常模型和黏塑性元件进行串联，以等时偏应力-应变曲线的拐点为界限，作为非线性蠕变的判别点，当应力水平超过岩石长期强度，认为此刻岩石发生非线性蠕变行为，由此，提出一种触发式黏塑性元件的概念，非线性蠕变状态瞬间切换，改进后的Maxwell模型如图6所示。

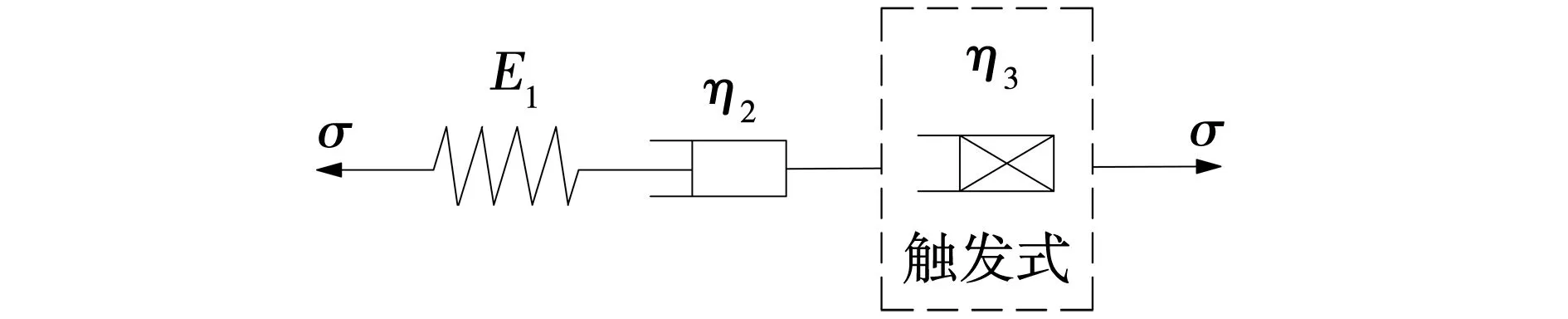
图6 改进Maxwell模型Fig. 6 Improved Maxwell model

当σ≤σS时，黏塑性元件失效，相应的岩石蠕变状态方程为

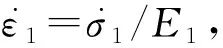
(3)

相应的蠕变方程为

(4)

式中：σ1、σ2——Hooke体和Newton体的应力；

E1——Hooke体的瞬时弹性模量。

当σ>σS时，黏塑性元件触发，相应的岩石蠕变状态方程为

σ=σ1=σ2=σ3，

ε=ε1+ε2+ε3，

(5)

相应的蠕变方程为

(6)

式(4)和(6)即为文中所建的岩石非线性蠕变本构模型。

3 参数解析与模型验证

文中所建模型包含E1、η2、η3、η0、λ、c和σS共7个待定参数，其中，E1依据Hooke定律求解，σS通过蠕变实验确定，图4中等时偏应力-应变曲线取拐点的方法已给出，其余参数采用一般的非线性最小二乘拟合求解。通过所建非线性蠕变模型识别模拟图3中蠕变曲线，得到模拟对比曲线，如图7所示。所建模型的参数如表3所示。

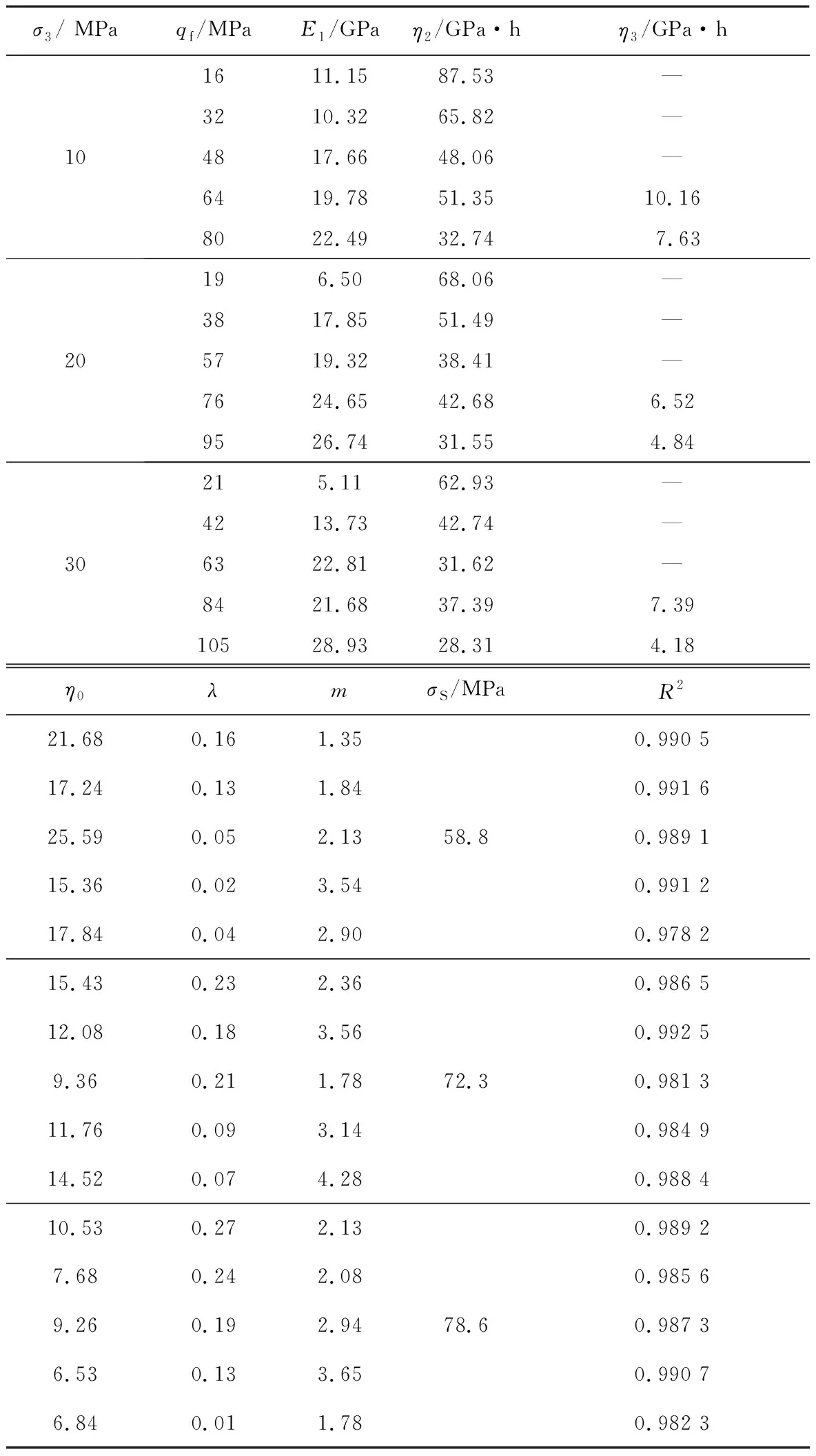
表3 模型参数Table 3 Model parameters

由图7可以看出，文中所建非线性模型对板岩蠕变曲线的拟合能力较强，精度较高，平均R2达到0.987 3。三种围压下，岩石在第四级加载尽管未出现加速蠕变，但由于第四级加载时偏应力超过了长期强度，文中认为偏应力超过长期强度便发生非线性蠕变行为，故第四、五级加载等级下蠕变数据采用式(6)进行模拟计算，前三级加载等级下通过式(4)进行识别。

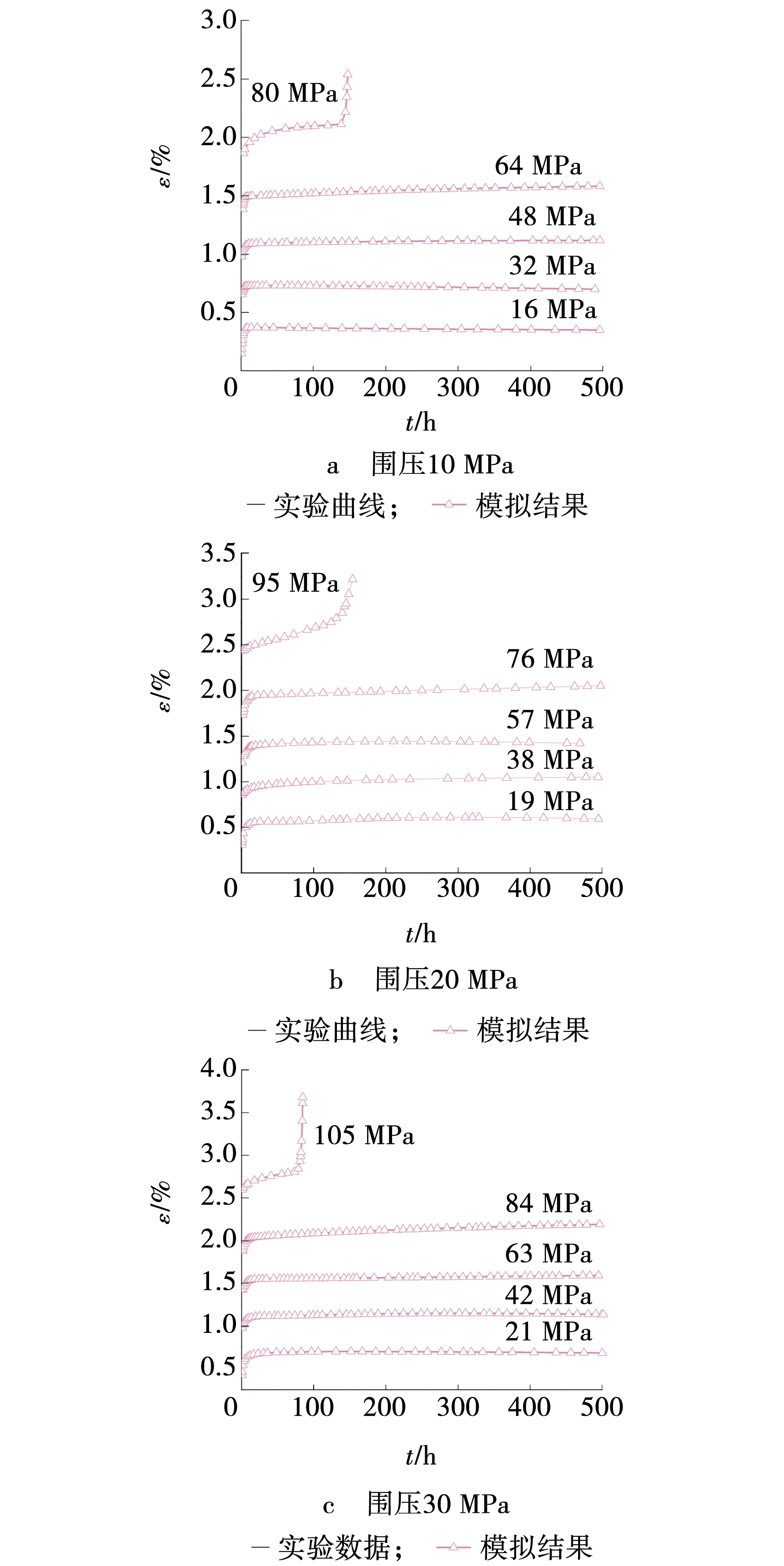
图7 模拟对比曲线Fig. 7 Simulation comparison curves

统计表3中不同围压不同偏应力下的瞬时弹性模量E1，其关系曲线如图8所示。

由图8可以看出，在同一围压下，瞬时弹性模量随着偏应力的增大而呈递增趋势。在围压30 MPa偏应力105 MPa条件下，瞬时弹性模量达28.93 MPa。

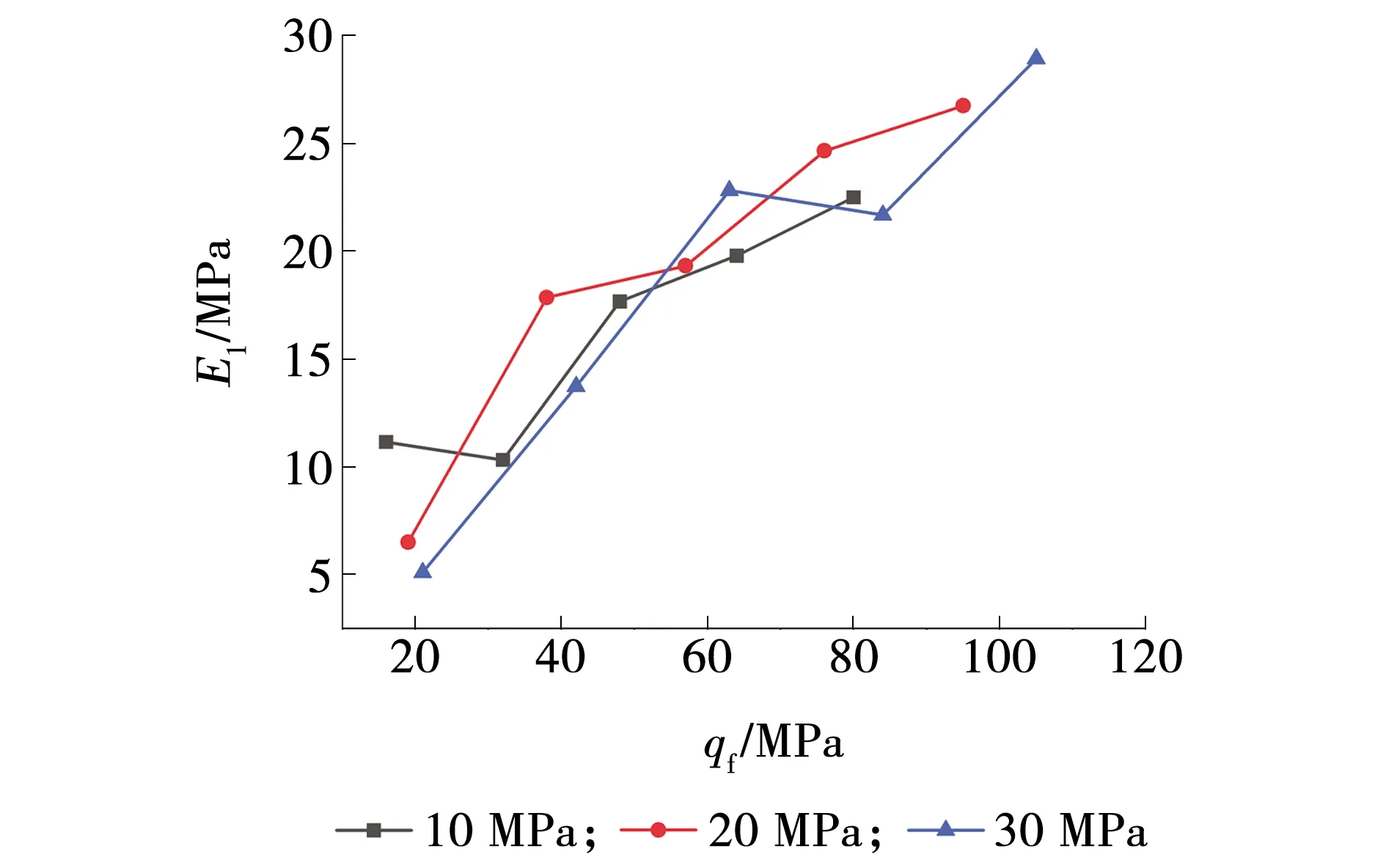
图8 瞬时弹性模量与偏应力关系曲线Fig. 8 Relation curves between instantaneous elastic modulus and deviatoric stress

围压10～30 MPa是水电工程倾倒变形边坡的常见应力水平，依据表3给出η0、λ、c的建议取值范围：η0的取值范围为[6.53，25.59]，λ的取值范围为[0.01，4.28]，c的取值范围为[1.35，4.28]，该建议取值范围仅针对围压10～30 MPa范围内的板岩。

倾倒变形边坡在演化过程中时效变形明显，具有“弯而不断”的特点，结合文献[14-15]的研究，认为倾倒变形边坡演化过程类似于岩石蠕变过程，阶段特性明显，倾倒变形演化视为悬臂岩层蠕变，同样分初始、等速和加速蠕变阶段，与岩石蠕变阶段特征契合，文中研究成果可为边坡倾倒变形力学模型建立及长期稳定性分析提供一定参考。

4 结 论

(1)文中开展不同围压条件下的板岩三轴压缩蠕变实验，实验发现板岩在偏应力接触瞬间，表现出瞬时弹性变形，随着时间推移表现出衰减、稳定蠕变阶段，当应力水平超过长期强度后发生非线性蠕变，最后还表现出加速蠕变行为。

(2)等时偏应力-应变曲线由0 h线性段和非线性曲线簇两部分组成，非线性曲线簇表现出逐渐偏于应变轴的趋势，通过对该曲线簇取拐点的方法，确定板岩在三种围压下的板岩长期强度分别为58.8、72.3和78.6 MPa，长期强度随着围压的增大而递增。

(3)通过统一流变力学模型理论，确定板岩基础蠕变模型，对Newton体非定常化，并引入黏塑性元件，提出触发式概念，建立新的改进后的非线性蠕变模型。经模拟验证，识别能力较强，平均R2达到0.987 3，证明改进后模型的合理性和可行性。