适应性神经元模型的Hopf分岔迁移控制

袁春华，冯博文，李翔宇

(沈阳理工大学 自动化与电气工程学院，沈阳110159)

神经元是神经信息处理的基本单位，神经信息的产生和传导包含着丰富的放电特性[1]。如果两个神经元的输入相同，产生的放电响应特性却不同，是因为其动力学规则不同[2]。神经元是一个动力系统，包含描述其状态的一系列变量和描述其状态变量如何随时间变化的规则[3]。其包含的变量根据功能和时标可以分为四类[4]：膜电势、兴奋性变量、恢复变量及适应变量。

改变外界刺激的幅值，神经元的相轨迹和放电状态将发生改变，而系统相轨迹的质变是由于神经元动力学经历了分岔的过程[5]。分岔类型决定了神经元的兴奋性质[6]。亚临界Hopf分岔是一个不稳定的极限环向一个稳定平衡点收缩并使之失去平衡，相轨迹变为一个大幅值的极限环吸引子。超临界Hopf分岔是稳定的平衡点失去稳定性，并产生一个小幅值的极限环吸引子，随着分岔参数的增大，极限环的幅值也逐渐增大。通过分岔控制改变系统发生分岔的位置和类型，可以改变神经元的动力学行为，从而得到想要的放电特性。

对于量化的数学模型，既要包括足够的细节考虑单神经元的动力学，又要尽量减少模型的复杂性且保留其本质特征[7]，使得模型计算方便，二者需要达到一个平衡。二维模型为模型真实性和计算效率之间提供了一个良好折中，它忽略了神经元的空间结构，可以通过相平面分析的方法用直观可视的方式去研究，既能复现丰富的放电模式，又满足研究动力学行为的非线性特性，有助于理解神经元的动力学现象[8-9]，是包括神经元放电所需的快慢变量的最“简化”模型[10]。

放电频率适应性是神经元动力学的一个显著特性，其在神经信息处理过程中起到了重要作用[11]。适应性神经元对持续常值刺激的响应频率呈现衰减的特性，最终的放电频率在某个值达到平衡并且低于初始值，甚至神经元在一段时间后停止了放电。放电频率适应性是放电神经元中普遍存在的一个现象，几乎任何类型的神经元都会呈现出该特性。最早在动物实验中观察到的放电频率适应性是在鼠的运动神经元中[12]，随后在猫的运动神经元[13]、听觉神经纤维[14]，夜蛾的听觉感受器[15]中均发现了放电频率适应性。Benda J等在模型中加入适应性离子电流研究神经元的适应特性[16]。

为使模型更加接近真实的神经元，本文将适应性电流引入二维Prescott模型，使模型由二维变为三维。通过相空间分析、分岔分析等方法对神经元的动力学特性进行研究，并应用代数判据对Hopf分岔的类型进行分析判断，然后通过迁移控制改变神经元模型发生Hopf分岔的位置，最后同时控制模型发生Hopf分岔的位置和类型。

1 三维Prescott神经元模型

在二维Prescott模型的基础上引入具有适应性的离子电流IA[17]，使二维模型变为三维，使模型更加接近真实的神经元。其动力学方程为

(1)

式中：V是神经元细胞膜电压；w是慢离子通道恢复变量；z是适应性电流离子通道恢复变量；gNa、gK、gL、ga分别为钠离子通道最大电导、钾离子通道最大电导、漏电导和适应性电流最大电导；ENa、EK、EL、Ea分别为相应的反电势；I为外部刺激电流，适应性电流为IA=gaz(V-Ea)；cm是神经元细胞膜电容；m∞(V)为钠离子通道激活变量的稳态值；w∞(V)为钾离子通道恢复变量的稳态值；z∞(V)为适应性电流离子通道恢复变量的稳态值；τw(V)为恢复变量的时间常数；τz(V)为适应性电流恢复变量的时间常数。

(2)

式中：βm、γm为快离子通道激活变量影响因子；βw、γw为慢离子通道恢复变量影响因子；βz、γz为适应性电流离子通道恢复变量影响因子。

本文中模型参数的取值为：cm=2μF/cm2、φw=0.15、φz=0.15、gL=2mS/cm2、gNa=20mS/cm2、gK=20mS/cm2、ga=10mS/cm2、EL=-70mV、ENa=50mV、EK=-100mV、Ea=-100mV、βm=-1.2mV、γm=18mV、βw=-10mV、γw=10mV、βz=-21mV、γz=15mV。

2 Hopf分岔的代数判据

对于高维非线性系统，求解特征根较为繁琐，引入Routh-Hurwitz代数判据[18]，可以不求解特征多项式的根，直接根据特征多项式系数判定Hopf分岔的存在性，从而简化高维系统的计算。

对于含参数的n维非线性系统，有

(3)

式中：f=(f1，f2，…，fn)T为光滑向量函数；μ∈R为分岔参数。

系统在平衡点处的Jacobian矩阵为

(4)

相应的特征方程为

p0(μ)λn+p1(μ)λn-1+…+pn-1(μ)λ+pn(μ)=0

(5)

式中p0(μ)～pn(μ)为特征方程各阶系数。其Hurwitz行列式为

Hn(μ)=

(6)

当j>n时，pj(μ)=0。其中各阶Hurwitz子式为

H1(μ)=p1(μ)

Hn-1(μ)=

(7)

则非线性系统(3)在μ=μ0发生Hopf分岔的条件为：

(1)特征值跨越条件

(8)

(2)横截条件

(9)

3 三维Prescott模型的Hopf分岔迁移控制

迁移控制前，通过上述计算求得系统在IHopf=113.2495μA/cm2处发生Hopf分岔，此时平衡点(VHopf，wHopf，zHopf)=(-35.6108，0.0059，0.1248)，特征值λ1，2=±0.9842i(i为虚数单位)、λ3=-0.2651。

根据文献[19]中三维非线性方程的Hopf分岔类型判定公式得β2=0.01259>0，因此该点为亚临界Hopf分岔。

图1为IHopf=113.2495μA/cm2时，模型发生Hopf分岔邻域内的V-w平面时域响应和三维相轨迹。

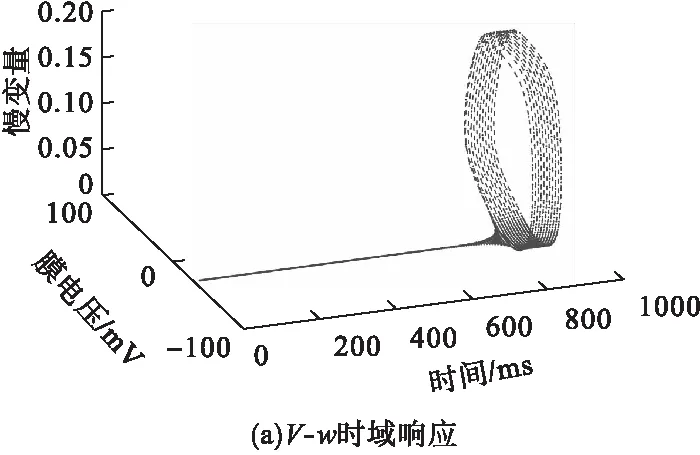
由图1可见，膜电压在此处发生振幅的突然跳变，从静息状态转变为大幅值振荡，此分岔为亚临界Hopf分岔，与计算结果一致。迁移控制前的模型分岔图如图2所示。

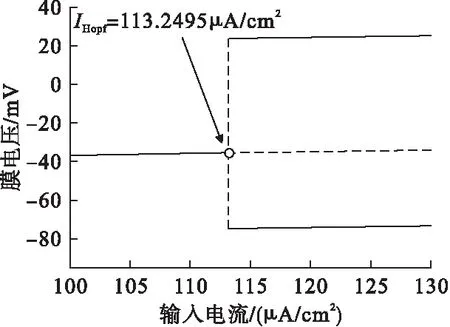
图2 迁移控制前的模型分岔

设系统施加控制后的状态方程为

(10)

式中：u为线性控制器；v为控制器的状态变量；K为线性控制器的增益；ξ为控制器时间常数的倒数。

采用线性反馈控制器对三维Prescott模型进行Hopf分岔的迁移控制，以避免Hopf分岔在某一段施加电流范围内出现，而是在需要处发生Hopf分岔。

设控制目标是将发生Hopf分岔处迁移到外刺激电流Irelocat=110μA/cm2时的新平衡点(Vrelocat，wrelocat，zrelocat)。

迁移控制前此点的特征值λ1，2=-0.013098±0.96795i、λ3=0.069958，为鞍焦点，模型此时不发生Hopf分岔。Irelocat=110μA/cm2时，(VHopf，wHopf，zHopf)=(-35.9260，0.005568，0.1062)，施加控制后的四维系统在迁移点处的Jacobian矩阵为

D4=

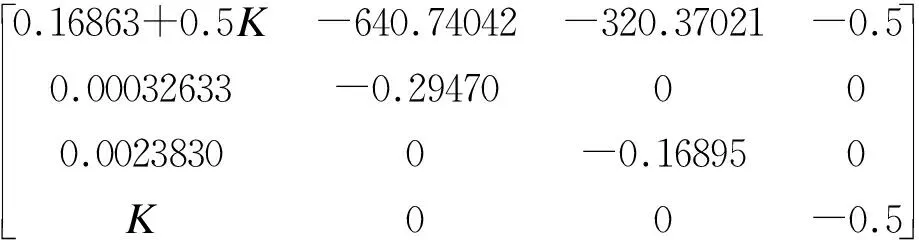
(11)

根据跨越条件，要求控制增益K满足

(12)

由H3=0，求得控制增益K=0.06996。代入其余不等式得p4=0.12683>0、H1=0.76004>0、ΔH2=0.23027>0，且由跨越条件求出的增益K同样满足横截条件

(13)

因此，求得的闭环线性反馈控制器的增益K满足横截条件。迁移点的特征多项式系数的Hurwitz子式随增益K的变化曲线见图3所示。

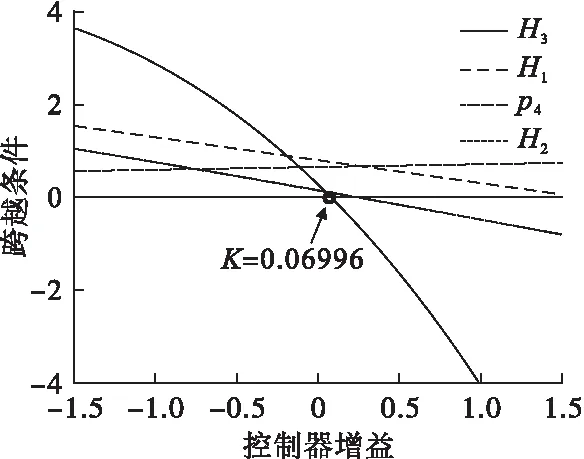
图3 迁移点的跨越条件随增益K的变化曲线

施加控制后迁移点特征值λ1，2=±0.9803i、λ3=-0.4915、λ4=-0.2685。经过控制后，此迁移点已成为中心焦点，三维Prescott模型随外刺激电流变化，到此处时将发生Hopf分岔。图4为迁移控制后神经元模型的分岔图。

4 迁移点的Hopf分岔类型控制

将Hopf分岔迁移到新的外刺激电流Irelocat=110μA/cm2处并不改变原分岔的类型，新的Hopf分岔仍为亚临界Hopf分岔。若要将新的分岔点控制为超临界Hopf分岔，则需对系统同时施加线性反馈和非线性反馈控制器，其控制方程为

(14)

式中：k1为线性反馈增益；k2为非线性反馈增益。

图4 迁移控制后的模型分岔图

根据上文分析可知，通过线性状态反馈控制，迁移点的奇点类型从鞍焦点转变为中心焦点；k1=0.06996时，在该点处施加外刺激电流可以诱发Hopf分岔，此分岔为亚临界Hopf分岔。施加非线性状态反馈控制，根据文献[19]中四维非线性方程的Hopf分岔类型判定公式得出β2的计算表达式为β2=0.14343k2+ 0.00026009。因此当k2<-0.001813时，β2<0，此时迁移点处分岔类型为超临界Hopf分岔。

图5是对模型同时施加线性反馈控制和非线性反馈控制后的分岔图。

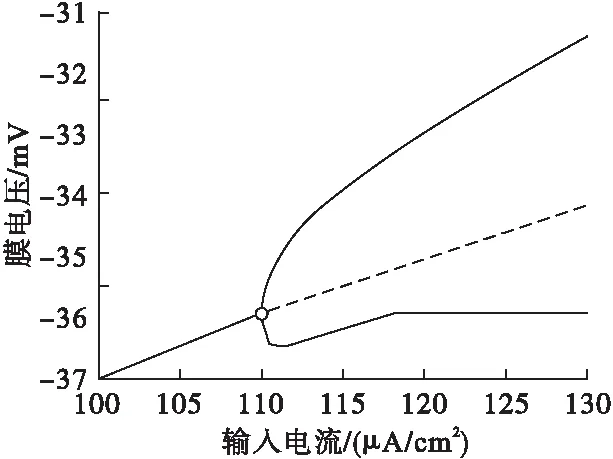
图5 控制模型同时发生Hopf分岔位置和类型改变

由图5可见，相较于原始系统，不仅分岔点位置发生了迁移，且亚临界Hopf分岔也转变为超临界Hopf分岔。施加控制后的V-w时域响应和相空间轨迹如图6所示。

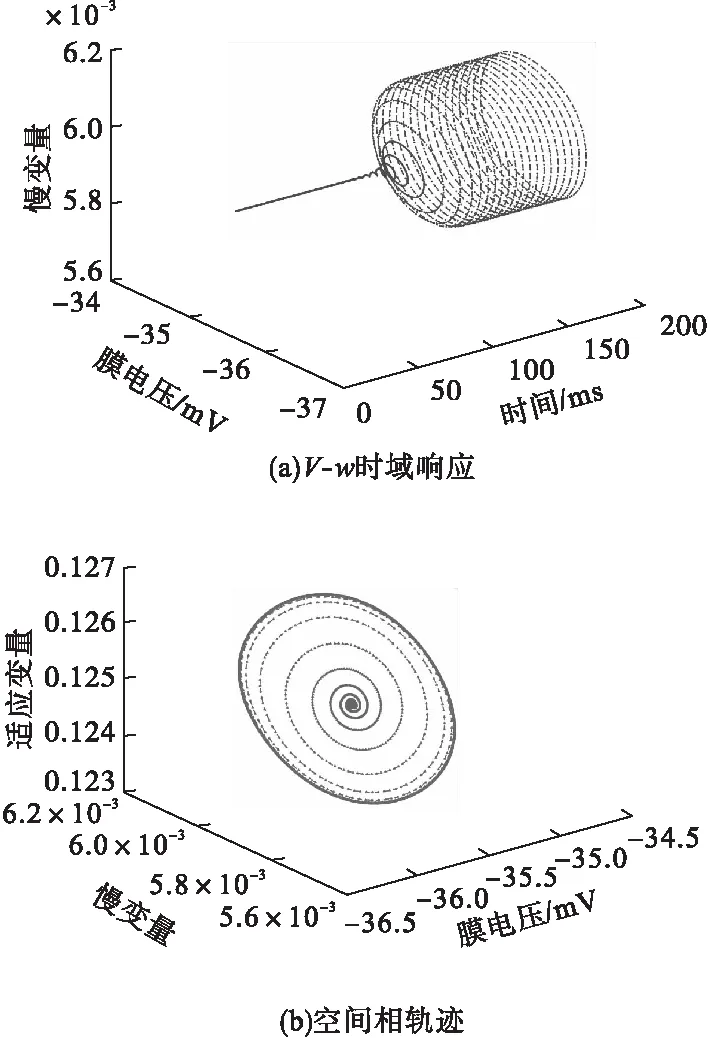
图6 控制模型发生超临界Hopf分岔处的时域响应和相空间轨迹

在分岔点处膜电压逐渐增大到稳定的极限环，为超临界Hopf分岔。

5 结论

以三维Prescott神经元模型为研究对象，通过解析法与数值模拟方法相结合，分析了模型的Hopf分岔特性。通过施加线性状态反馈对模型进行迁移控制，改变了Hopf分岔的发生位置，从而改变神经元的放电特性。同时对模型施加线性反馈控制和非线性反馈控制，在Hopf分岔发生位置改变的同时，使不稳定的亚临界Hopf分岔变为稳定的超临界Hopf分岔。