PdCl2在不同浓度LiCl溶液中的电化学行为研究

华艳会，张馨月，谢 天，何金桂，张 武

(沈阳理工大学 a.工程实践中心；b.材料科学与工程学院，沈阳 110159)

钯是重要的铂族金属，在汽车、珠宝、催化剂等领域应用广泛。电沉积钯作为回收钯和合成钯相关材料的重要手段[1]，一直是研究人员和工程技术人员关注的课题。钯具有正的电压，在纯水体系中即可沉积出金属钯[2]。但在纯水体系中沉积钯面临一个难以解决的问题——沉积出的金属钯在常温下容易发生氢脆裂现象，即金属钯吸收微量的氢后形成晶格常数不同的α-贫氢相和β-富氢相，从而造成金属钯沉积层产生裂纹[2-4]。近年来，有研究表明[5]，含氯离子体系可以有效抑制钯在电沉积过程中的氢脆现象。

钯电沉积过程与其电化学行为密切相关，已有较多文献报道关于钯的电化学行为。Nazarov B F等[6]研究表明钯的还原过程分为两个步骤进行，即

(1)

M-PdCl2+2e→M-Pd(0)Cl22-→
M-Pd(0)+2Cl-

(2)

在动力学上，步骤(1)的速率明显快于步骤(2)。

在含有高浓度氯离子的溶液中，钯的还原过程按以下两个步骤进行[6]。

(3)

M-PdCl3-+2e→M-Pd(0)Cl33-→
M-Pd(0)+3Cl-

(4)

Jayakumar M等[7]研究了钯化合物在金属钯电极上的还原过程，发现钯电极对氯离子具有很强的吸附作用，吸附过程可表示为

Cl-(aq)→Cl(ads)+e

(5)

阳极反应(钯沉积物的氧化过程)主要为

(6)

以上研究初步阐明了钯离子在氯离子溶液中的电化学还原过程。但目前针对钯在不同浓度氯离子体系中的电化学行为研究较少。本文以PdCl2为原料，采用循环伏安法研究钯在四种不同浓度LiCl溶液中的电化学行为，并利用旋转圆盘电极技术研究钯化合物的还原反应动力学过程。

1 实验方法

1.1 实验主要原料

实验主要原料为PdCl2和LiCl，均为分析纯，购自麦克林试剂有限公司，两种试剂未经进一步提纯。

1.2 实验方法

将工作电极进行抛光处理后，用蒸馏水润洗3次，吹干，表面洁净后进行电化学测试。

采用CHI760E电化学工作站(上海辰华仪器有限公司)进行电化学测试，电解池体积为60mL，石墨棒作为对电极(CE，直径5mm)，玻碳电极为工作电极(WE，直径2mm)，Ag/AgCl为参比电极(RE，直径2mm)。实验装置示意图如图1所示。采用RRDE-1A型旋转盘电极装置(泰州市德仪分析仪器有限公司)进行旋转盘电极实验，工作电极为玻碳电极(直径3mm)。

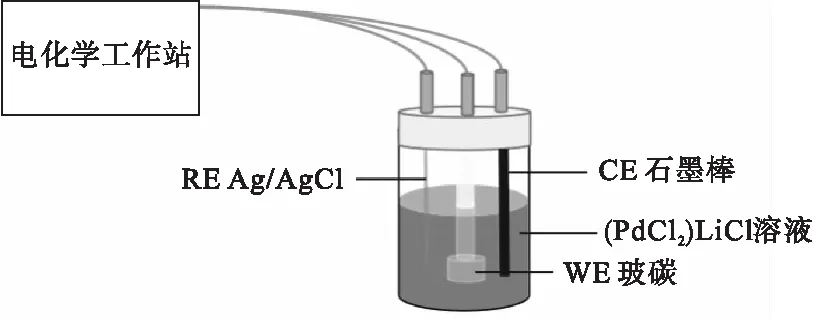
图1 电化学实验装置示意图

2 结果与讨论

2.1 不同浓度LiCl溶液的循环伏安曲线

LiCl溶液具有较宽的电化学窗口，是熔盐电化学常用的溶剂。在研究PdCl2的电化学行为之前，首先进行LiCl溶液的电化学窗口测试，LiCl溶液浓度分别取为0.05mol/L、0.5mol/L、5mol/L、8mol/L，测试得到其循环伏安曲线如图2所示。文中电压数值均为相对于Ag/AgCl参比电极的电压(Ag/AgCl参比电极电压为0.22V)。

由图2可以看出，四种不同浓度的LiCl溶液分解电压相差较小，其中浓度为0.05mol/L的LiCl溶液电流较小，因其浓度较低。四种浓度的LiCl溶液在-1.5～1.0V范围内均未发生分解，故可作为研究PdCl2电化学行为的理想溶剂。

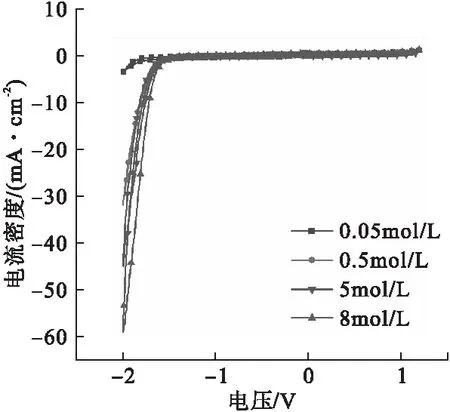
图2 不同浓度LiCl溶液的循环伏安曲线

2.2 PdCl2在不同浓度LiCl溶液中的循环伏安行为

室温(25℃)条件下，以不同的扫描速率测试PdCl2在四种不同浓度LiCl溶液中的循环伏安曲线，结果如图3所示。

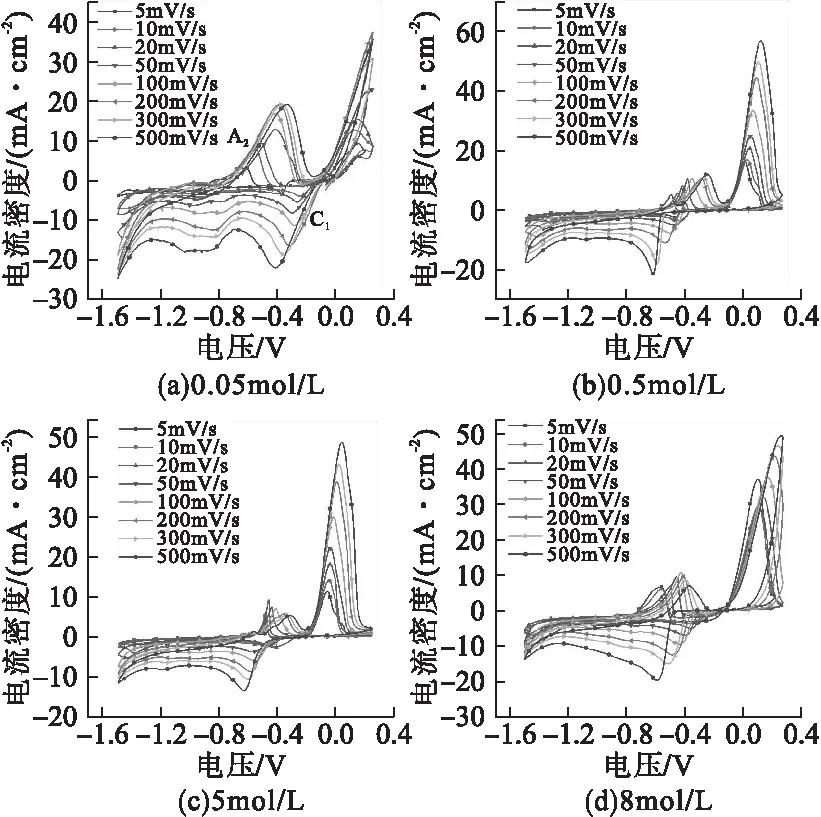
图3 不同扫描速率下PdCl2在不同浓度LiCl溶液中的循环伏安曲线

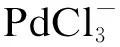
以LiCl溶液浓度0.05mol/L的实验结果为例，其在25℃下循环伏安曲线中第一个阴极峰(C1)和第二个阳极峰(A2)的电流密度对比如表1所示。表中最后一列为C1和A2的电流密度之比，即第二列和第三列数值的比值。

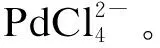
(7)

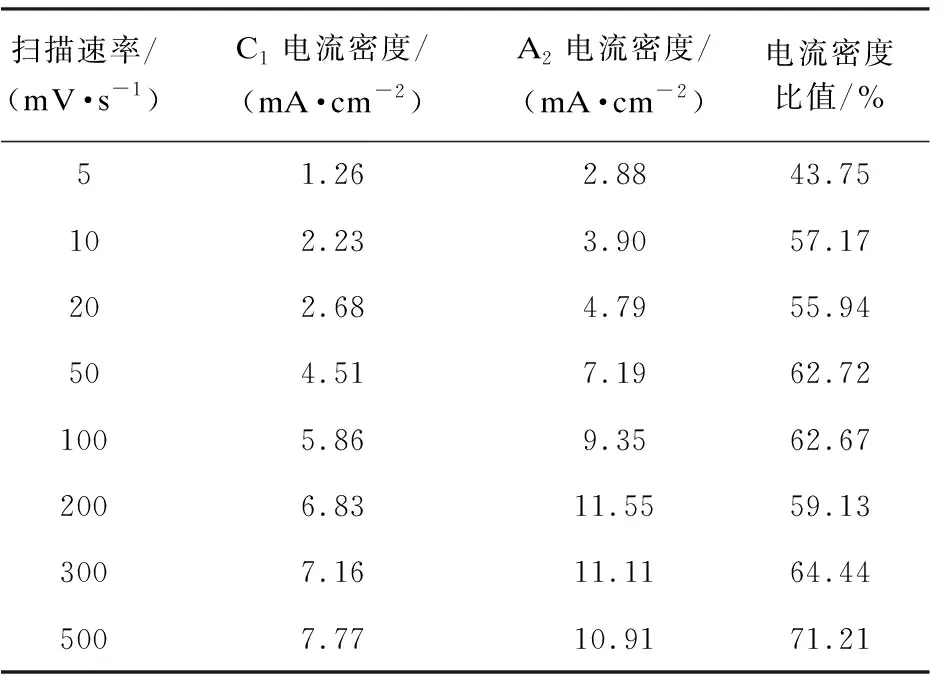
表1 阴极峰(C1)和阳极峰(A2)电流密度对比

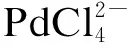
(8)

从过程(7)和(8)可以看出，PdCl2的络合过程及金属钯的溶解过程均较慢，从而可能成为金属钯沉积物重新氧化进入离子液体的速率控制步骤。

电化学反应的可逆性对于研究电化学行为十分重要。电极反应的可逆性可以用能斯特方程进行判断[8]，文献[5]以能斯特方程为基础总结了可逆电极反应一般的典型特征如下：

(1)阴极峰和阳极峰的峰电压差值为59/n，其中n为电子转移数；

(2)阴极峰与阳极峰电流的比值为1；

(3)峰电流正比于扫描速率的平方根。

按照以上几个原则，本文中钯化合物的还原反应不符合上述特征，故为不可逆过程。

钯离子在溶液中的扩散系数是研究还原过程动力学的重要参数，可用以下方程计算钯离子在溶液中的扩散系数[7]。

(9)

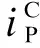
根据LiCl溶液浓度为0.05mol/L时的实验数据(图3a)，对峰值电流密度和扫描速率平方根的关系进行线性拟合，结果如图4所示。

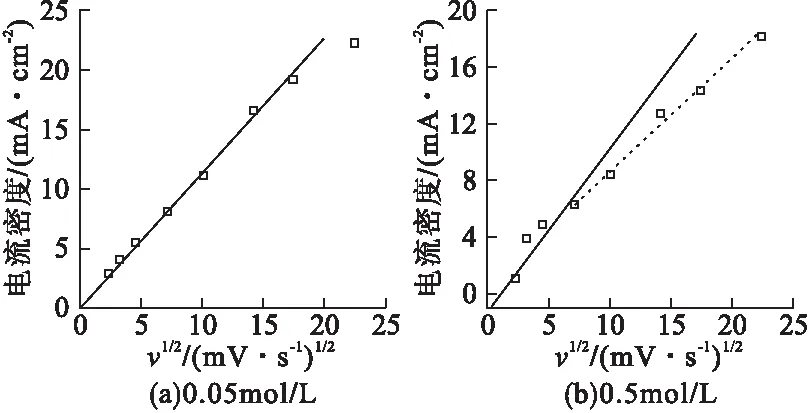
图4 0.05mol/L LiCl溶液中峰值电流密度随扫描速率平方根的变化关系

拟合得到第一个阴极峰和第二个阴极峰的斜率分别为0.813和0.826。据此计算得到第一个阴极峰对应的扩散系数DC1为1.73×10-6cm2/s，第二个阴极峰对应的扩散系数DC2为2.84×10-6cm2/s。关于钯离子在电解液中的扩散系数，目前可用于比较的数据十分有限。Jayakumar M等[7]的研究表明，100°C时PdCl2在1-丁基-3-甲基咪唑氯盐离子液体中的扩散系数为1.637×10-7cm2/s，说明1-丁基-3-甲基咪唑氯盐离子液体在100℃时的粘度仍比本文采用的LiCl溶液粘度大，因而离子扩散速率慢，扩散系数较本文实验得到的数值小。

2.3 旋转盘电极实验

旋转盘电极实验在研究电化学反应动力学方面具有独特优势，通过旋转操作，可使反应迅速达到动态平衡。PdCl2溶液在不同浓度的LiCl溶液中不同旋转条件(转速)下的循环伏安曲线如图5所示。因设备量程限制，LiCl溶液浓度为0.5mol/L和5mol/L时未测量转速为400rpm下的数值(图5b和图5c)，LiCl溶液浓度为8mol/L时未测量转速为200rpm和400rpm下的数值(图5d)。

图5 旋转盘电极下PdCl2在不同LiCl溶液中的循环伏安曲线

由图5可见，图5a和图5b中曲线出现明显的扩散控制区域。Levich提出了关于旋转圆盘上对流扩散的精确理论[9]，见式(10)所示。Levich方程主要用于分析由传质控制的电化学反应[10-11]，随后由Koutecky继续扩展，当反应为混合动力学控制机制时，使用Koutecky-Levich方程精确描述还原反应的动力学[9-11]，见式(11)所示。

i=0.62nFAD2/3η-1/6Cω1/2

(10)

式中：i为电流，A；η为溶液的运动粘度，cm2/s；C为溶液浓度，mol/cm3，本文中PdCl2溶液浓度为5×10-5mol/cm3；ω为转速，rad/s。

(11)

式中k为反应速率常数，cm/s。

根据图5中第二个阴极峰的实验数据，按照式(10)，对电流密度和转速平方根的关系(Levich方程)进行线性拟合，结果如图6a所示；按照式(11)，对电流密度的倒数和转速平方根的倒数之间关系(Koutecky-Levich方程)进行线性拟合，结果如图6b所示。

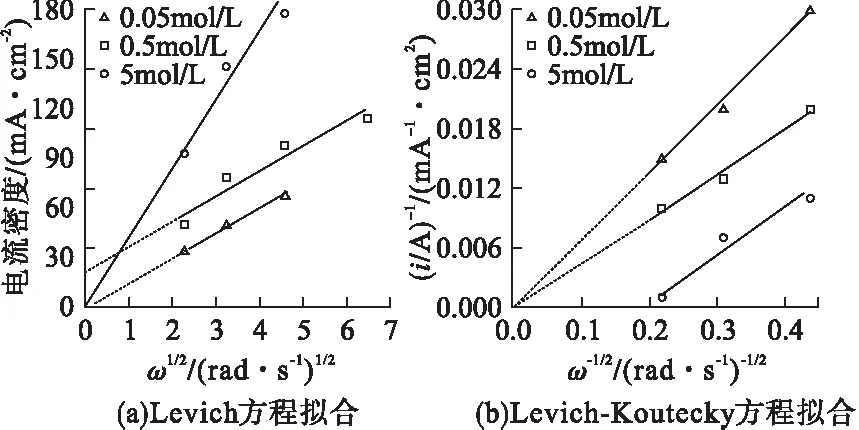
图6 不同浓度LiCl溶液中PdCl2电化学还原对应的Levich方程和Levich-koutecky方程拟合图

由图6可以看出，当LiCl溶液浓度为0.05mol/L和5mol/L时，Levich方程的延长线靠近坐标原点，根据Levich公式可知，此时反应主要受扩散控制；当LiCl溶液浓度为0.5mol/L时，相应Levich方程拟合直线截距较大，说明此时反应为传质与反应速率混合控制[8]。

由图6拟合得到Levich方程和Levich-Koutecky方程的线性关系如表2所示。

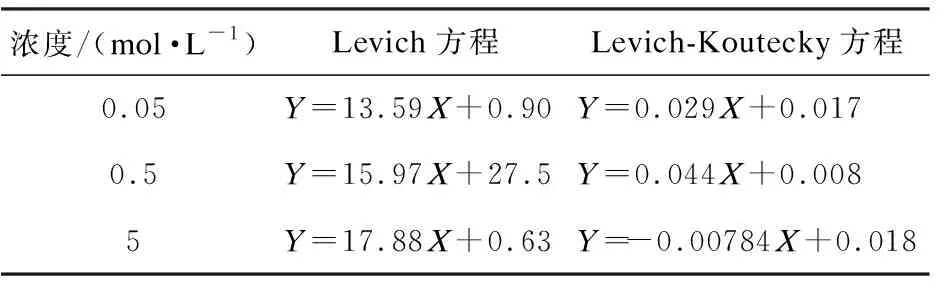
表2 不同浓度LiCl溶液下循环伏安曲线中第二个阴极峰的Levich拟合方程和Levich-Koutecky拟合方程

由表2中Levich方程和Levich-Koutecky方程的线性关系进一步计算得到钯络合离子在不同浓度LiCl溶液中的扩散系数和反应速率常数，结果如表3所示。

表3 不同浓度LiCl溶液下电极反应的扩散系数和反应速率常数

由表3可以看出，钯络离子的扩散系数随着LiCl溶液浓度的增加而增加，表明高浓度的LiCl溶液对钯络合物的还原具有积极作用。随着LiCl溶液浓度的增加，反应速率常数增大，反应速率加快。

3 结论

采用循环伏安法研究了PdCl2在不同浓度LiCl溶液中的电化学行为，结论如下。

(3)静态循环伏安曲线有两个阳极峰，第一个阳极峰对应Cl-在钯沉积物上的解吸过程，第二个阳极峰对应金属钯的电化学氧化反应。

(4)循环伏安曲线结果表明，钯的电化学还原反应不可逆，在0.05mol/L LiCl溶液中，钯化合物在溶液中的扩散系数为10-6cm2/s数量级。

(5)旋转盘电极实验结果表明，钯络合物还原的阴极反应属于混合动力学过程。随着LiCl溶液浓度的增加，钯离子在溶液中的扩散系数和反应速率常数均增大，扩散系数为10-6cm2/s数量级，反应速率常数约为10-4cm/s数量级。