黄土孔径和持水特性的分形维数研究
廖红建,刘少华,何玉琪,孙俊煜
(西安交通大学 人居环境与建筑工程学院,陕西 西安 710049)
黄土地区发生的许多地质灾害,如黄土湿陷、黄土滑坡、崩塌等都与黄土中含水状态的变化有关[1]。自然界中的黄土大部分都是以非饱和土的形式出现,土中的水分大多存在于土中大小不一、数量繁多的孔隙中,孔隙的分布特征是决定土中水分存在和变化规律的主要因素[2]。因此,有必要对黄土在各种外界因素的作用下内部细观结构的变化进行预测、观察和评价,并对内部细观结构变化引起的土体含水状态变化进行预判断。
分形理论用于描述“不规则的、分数的、支离破碎的”物体[3]。土中孔隙分布十分不规则,大小孔径数量级之间差异很大,符合分形理论的基本特点。大量研究表明,形状、大小各异的颗粒骨架和孔隙所组成的土体具有明显的分形特征[4-9]。岩土分形理论中,若能确定土体孔隙体积的分形维数D,则可对岩土体的宏观物理力学特性进行判断和预测。
土的孔径分布曲线,可以确定土的孔径和相对应的孔隙体积百分数,从而求出土的孔隙体积-孔径分布的分形维数。因此,本文通过压力膜仪试验,结合孔径分布计算理论,做出孔径分布曲线,并结合分形理论,总结土体的不同干密度和含水率对其内部孔隙的影响规律,分析孔隙的变化对土体持水特性的影响。
1 孔径分布
1.1 孔径计算理论
1871年,William Thomson提出了开尔文公式

(1)
其中:r为土中孔隙的半径(μm);Ts为毛细管的液相表面张力(J/m2);α为土体固相和液相之间接触角;vw是水蒸气的偏摩尔体积(m3/mol);R为通用气体常数(J/(mol·K));T为热力学温度(K);RH为孔隙水蒸气的相对湿度(%);ua-uw为基质吸力(kPa)。
由于土颗粒中可能存在的结合水膜,实际的孔隙尺寸rp还需要考虑水膜厚度t的影响[10]
rp=r+t
(2)
土体结合水膜的厚度可以直接用厚度法来计算[11],它与含水率和土的相对比表面积有关

(3)
其中:wa为结合水的含水率(%);ρew为结合水的密度(g/cm3);As为土样的相对比表面积(m2/g)。
土样的比表面积As与土体的细观结构相关,可以通过气体吸附法进行测定。
崔德山[12]根据实验结果得到了结合水密度ρew和含水率w之间的估算关系如下
ρew=0.000 2w2-0.027 2w+1.800 5
(4)
在压力膜仪试验中,每一级吸力均对应一个孔隙尺寸rp,倘若假定每一级吸力作用下,对应孔隙尺寸范围内孔隙水均完全脱水,由于土样初始饱和,则该孔隙尺寸范围内孔隙的总体积Vvi等于脱出的水的总体积ΔVwi
Vvi=ΔVwi
(5)
因此,结合土水特征曲线和压力膜仪试验,即可通过式(1)~式(4)来估算土中每一级吸力下孔隙的半径,又可以通过式(5)估算对应孔隙半径的孔隙体积,即可求得以孔隙的半径和孔隙体积为坐标的孔径分布曲线。
1.2 孔径分布分形理论
基于Sierpinski垫片模型和分形理论,当观测尺度为L时,土中的颗粒含量N(L)可表示为[13]
N(L)=C*L-D
(6)
其中,C*为常数,D为分形维数。则此时土中颗粒的总体积V(L)可以表示为
V(L)=C1L3-D
(7)
土中总的孔隙体积为土的体积减去土颗粒总体积,故总的孔隙体积Vv(L)可以表示为
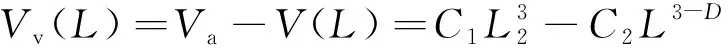
(8)
其中:Va为土样总体积;L2为总尺度,等于土样的总尺寸;C1和C2为常数。根据Sierpinski垫片模型,当观测尺度为L2时,观测到的总体孔隙体积为0,则
C1=C2
(9)
土中孔径大于等于r的孔隙所占体积含量Vv(≥r)可表示为

(10)
其中:n为孔隙比;Vv为孔隙体积。为了便于计算,将式(10)变换为

(11)
对式(11)两边取自然对数,可得

(12)
在取对数的前提下,式(12)中的n和L2仅仅是对曲线进行了上下平移,并不改变曲线的斜率。因此,根据孔径分布曲线,即可做出ln[Vv(≤r)/(Vv)]和lnr的关系曲线。再根据式(12)可知,由该关系曲线的斜率(3-D)可求出孔隙体积-孔径的分形维数D。
利用分形维数D,即可分析土体内部孔隙的变化规律和孔隙的变化对土体持水特性的影响。
2 压力膜仪试验
2.1 试验仪器与方案
压力膜仪试验所用仪器设备为美国土壤水分公司(SME)推出的1500F1型压力膜仪。
为了研究不同的压实度下,土中细观孔径分布对于土体持水特性的影响,采用了以干密度作为变量。击实前,3组试样含水率均设定为18.5%,再分别对试样进行45、60、75次的击实后,3组试样的干密度分别为1.674 g/cm3、1.786 g/cm3、1.837 g/cm3。
为了分析土体中含水率不同的情况下,土中细观的孔径分布对土体持水特性的影响,采用含水率作为变量,以最优含水率17.3%为界限,依次在含水率为15.8%、17.3%、18.5%的情况下,对试样击实60次,击实后土样的密度分别为2.02 g/cm3、2.06 g/cm3和2.12 g/cm3。
2.2 试样制备与试样条件
试验所用的土样取自西安市地铁四号线工程行政中心站地以下10 m处。通过基本物性试验,测得该土样的土粒相对密度ds为2.68,最大干密度ρdmax为1.842 g/cm3,液限wL为27.5%,塑限wp为17.2%,塑性指数Ip为10.3。对土样进行风干、研磨后进行筛分析试验,得到其颗粒组成情况如表1所示。

表1 非饱和黄土的颗粒组成Tab.1 Particle composition of unsaturated loess
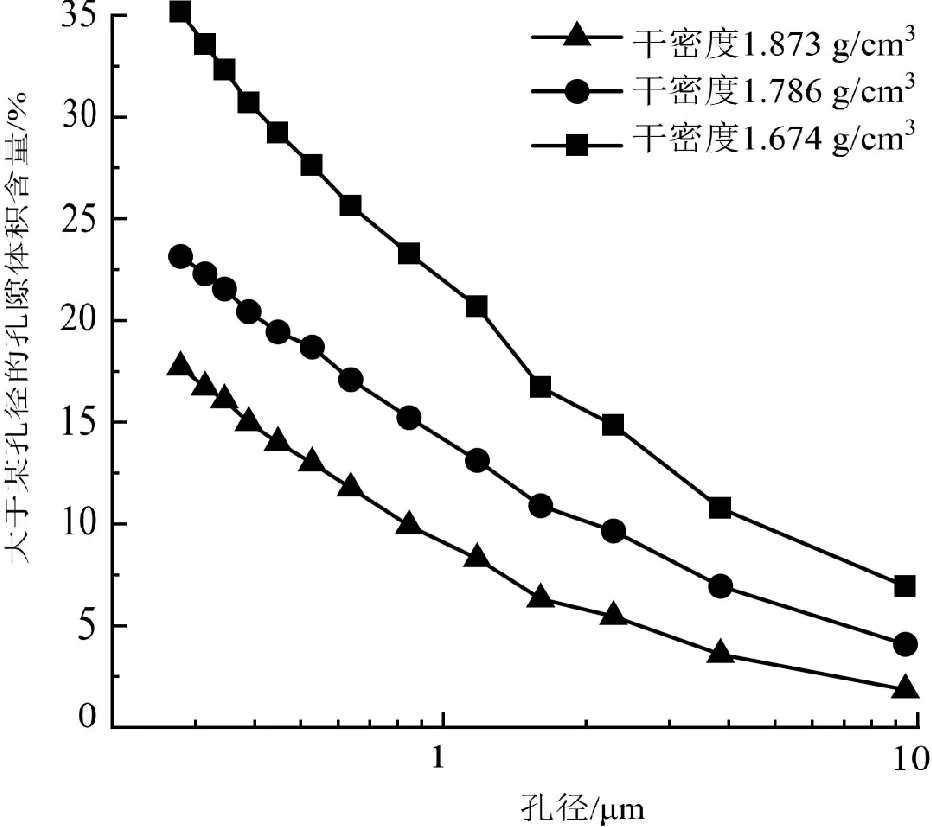
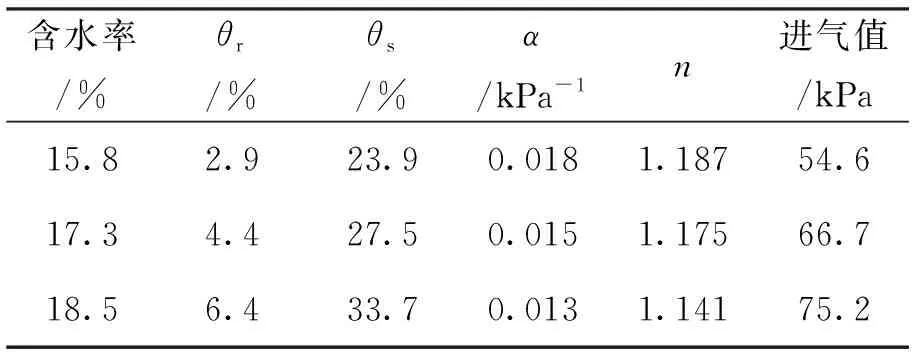
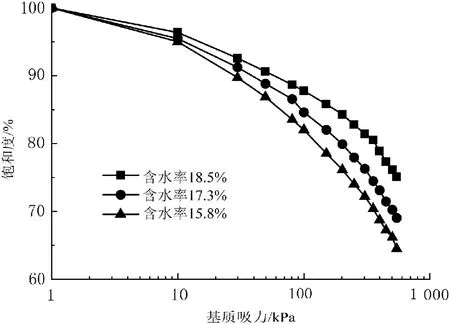
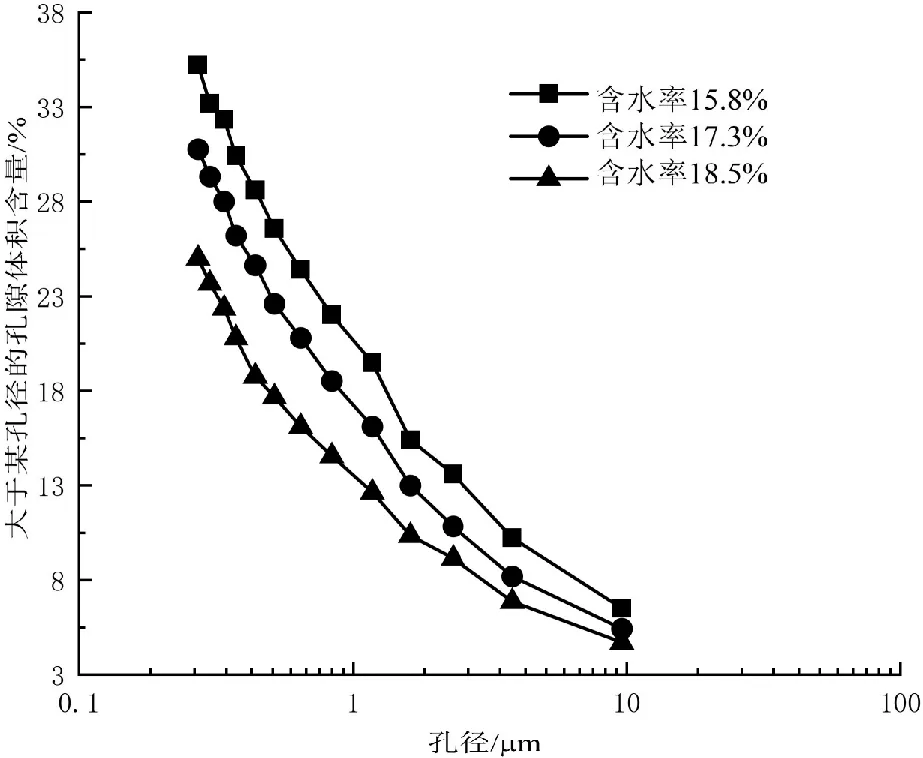
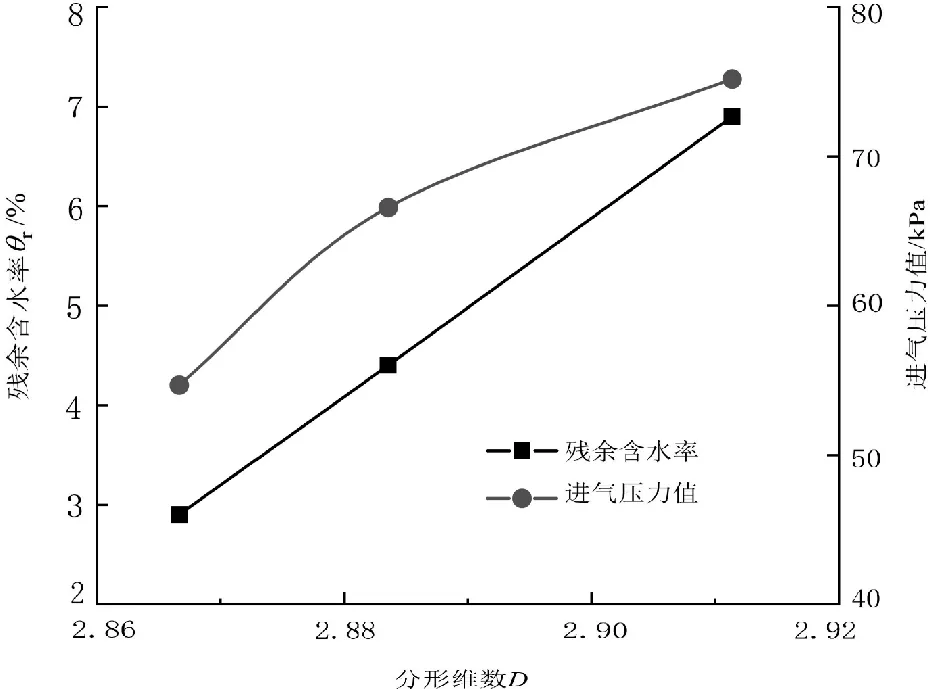
粒径大于0.075 mm的粉黏粒含量未超过50%,且土样的塑性指数满足10 通过试验,得到的3组不同干密度土样的土水特征曲线如图1所示。结合孔径分布的计算理论,可以计算出孔径分布曲线。 图1 含水率为18.5%时不同干密度土样的土水特征曲线Fig.1 Soil-water characteristic curves of soil samples with different dry densities with water content of 18.5% 为了从试验结果中提取表征土体持水特性的进气值和残余含水率等参数,使用van genuchten (VG)模型[15]对土样的土水特征曲线进行非线性拟合。 (13) 其中:θw为体积含水率(%);θr为残余体积含水率(%);θs为饱和体积含水率(%);α在数值上约等于进气压力值的倒数(kPa-1);φ为基质吸力;n为孔径分布参数;m为试验参数。 用VG模型对不同干密度试样的土水特征曲线(见图1)进行拟合,得到3组不同干密度土样的相关参数,如表2所示。 表2 不同干密度土样VG模型计算参数Tab.2 Calculation parameters of VG model for soil samples with different dry densities 结合试验数据和孔径分布理论,得到的孔径分布曲线如图 2所示。 由图2可知,该组试样的孔径分布曲线在试验范围内均呈下凹型,说明压实后的土样中,大孔径的孔隙体积含量小,小孔径的孔隙体积含量多。且随着干密度的增大,相同孔径时曲线的斜率明显减小,说明随着击实次数的增多,试验范围内各孔径的孔隙体积含量均减小。且试样密实度增大的同时,相同的基质吸力下能排出的水的体积明显减小。 图2 不同干密度土样的孔径分布曲线Fig.2 Pore diameter distribution curve of soil samples with different dry densities 为了进一步分析不同干密度试样的孔径分布特征和其持水特性之间的关系,利用分形理论对试样的孔隙体积-孔径进行分析。结合式(12)和图2,以lnr为横坐标,以ln[Vv(≤r)/(Vv)]为纵坐标,可对不同干密度试样的孔径分布特征进行分形分析,结果如图3所示。 根据图 3,不同干密度的土样,在孔径较小的时候,其lnr和ln[Vv(≤r)/(Vv)]呈较为明显的直线关系,说明土样的孔隙分布在小孔径的前提下具有明显的分形特征,其内部孔隙体积百分比含量的分形维数D分别为2.873、2.917 1和2.933 2。可以发现,孔隙体积百分比含量的分形维数D随着试样干密度的增大而增大。 图3 不同干密度土样的孔隙体积-孔径分形维数Fig.3 Fractal dimension of pore volume and pore diameter of soil samples with different dry densities 为了分析土体内部的孔隙体积百分比含量的分形维数D与土体持水特性的关系,将根据VG模型得到的土体持水特性参数——残余含水率θr和进气压力值参数α的关系整理如图4所示。 由图4可知,不同干密度的黄土试样,内部的孔隙体积百分比含量的分形维数D与残余含水率呈正相关,且有较为明显的线性关系,分形维数D越大,残余含水率越大,土体的持水性能越强。分形维数D与试样的进气压力值也呈正相关,进气压力值是土体中开始出现气泡的吸力,对于饱和土而言,进气压力值越大,其持水能力越强,最大孔隙的半径越小,但它们之间不呈线性关系。 图4 孔隙体积-分形维数与不同干密度土体持水特性的关系Fig.4 Relationship between fractal dimension of pore volume to pore diameter and water-holding characteristics of soils with different dry densities 综上所述,土体内部的孔隙体积百分比含量的分形维数D可以反映不同压实度下土中孔隙分布特征,也可以用于评价土的持水特性,土体较为松散时,土中孔隙体积较大,此时土的持水能力较弱,分形维数D较小;相反,土体较为紧密时,土中孔隙体积较小,此时土的持水能力较强,分形维数D较大。 3组不同含水率的黄土试样的土水特征曲线如图5所示。图中,3条土水特征曲线差异较小,初始含水率较低的土样略陡,含水状态变化略明显。 同样,利用VG模型对图5中的土水特征曲线进行非线性拟合,得到3组不同含水率的黄土试样的持水特性相关参数,如表3所示。 表3 不同含水率土样VG模型计算参数Tab.3 Calculation parameters of VG model for soil samples with different water content 图5 击实60次时不同含水率土样的土水特征曲线Fig.5 Soil-water characteristic curves of soil samples with different water content after 60 compaction times 结合试验数据和孔径分布理论,得到3组不同含水率试样的孔径分布曲线如图6所示。 由图6可知,该组试样的孔径分布曲线在试验范围内同样呈下凹型,孔隙的累积速度较慢,不同含水率的试样中,孔径大于0.01 mm的孔隙含量均在4%~6%之间。说明不同的含水率条件下,土中的大孔隙的体积所占比例基本保持不变。随着含水率的增大,相同孔径时曲线的斜率变化不明显,可以认为,各孔径值对应的孔径分布曲线的斜率基本保持不变。这说明,在增湿条件下,土中结构状态发生改变时,不同孔径的孔隙体积基本按等量变化。综上,初始含水率越大的土样,土中孔径整体略小,持水能力稍有提高。 图6 不同含水率土样的孔径分布曲线Fig.6 Pore diameter distribution curve of soil samples with different water content 同样,结合式(12)和图 6,以lnr为横坐标,以ln[Vv(≤r)/(Vv)]为纵坐标,对不同含水率试样的孔隙分布特征进行分形分析,结果如图7所示。 图7 不同含水率土样的孔隙体积-孔径分形维数Fig.7 Fractal dimension of pore volume and pore diameter of soil samples with different water content 同样地,排除试验数据中孔径较大的数据点,不难发现,不同含水率的土样,lnr和ln[Vv(≤r)/(Vv)]也呈较明显的直线关系。根据图 7计算可得,其内部孔隙体积百分比含量的分形维数D分别为2.866 6、2.883 4和2.911 6。土样的初始含水率越大,土的孔隙体积-孔径分形维数D越大,在湿度增大的同时,大于某一孔径的孔隙体积百分比减小。由此推断,在增大水分时,在观测区域内,土中孔隙的整体孔径水平减小。 为了进一步分析不同含水率的土体孔隙体积-孔径分形维数D与持水特性的关系,整理土的残余含水率与进气压力值与分形维数D的关系,如图8所示。 图8 孔隙体积-分形维数与不同含水率土体持水特性的关系Fig.8 Relationship between fractal dimension of pore volume to pore diameter and water-holding characteristics of soils with different water content 由图8可知,孔隙体积百分比含量的分形维数D与残余含水率正相关,且表现为明显的一次线性关系,分形维数D越大,残余含水率越大,土体的持水性能越强,这一点与不同干密度土样的试验结果相一致。此外,土样的进气压力值与分形维数D同样正相关,但两者之间不呈线性关系。 由此可见,土体内部的孔隙体积百分比含量的分形维数D可以反映不同湿度下土中孔隙分布特征,也可以用于评价土的持水特性。土体较为干燥时,土中孔隙体积较大,此时土的持水能力较弱,含水状态变化大,分形维数D较小;相反,土体较为湿润时,土中孔隙体积较小,此时土的持水能力较强,含水状态变化不明显,分形维数D较大。在土的各项持水特性指标中,残余含水率与分形维数相关关系简洁、明显。因此,分形理论可以有效的用于分析土中孔隙分布特征这一细观因素,并对土的残余含水率进行可靠的评价。 本文以分形理论为基础,分析了不同压实条件和不同含水率条件下土的孔隙变化特征和含水状态变化规律,得出了主要结论如下: 1)分形维数D可以反映不同压实度和不同湿度下土中孔隙分布特征,也可以用于评价土的持水特性。土体较为松散、干燥时,土中孔隙体积较大,此时土的持水能力较弱,分形维数较小;相反,土体较为紧密、潮湿时,土中孔隙体积较小,土的持水能力较强,分形维数较大。 2)分形维数与残余含水率正相关,且表现为明显的一次线性关系,分形维数越大,残余含水率增大的同时,土体的持水性能也增强。分形理论可以对土的残余含水率进行可靠的评价。 3)分形维数与土样的进气压力值同样正相关。但不同的是,干密度组试验中,随着分形维数的增大,土样的进气压力值会显著增大,但在含水率组试验中,随着分形维数的增大,土样进气压力值的增大幅度越来越小。压实和增湿两种不同的作用,对于改变土体进气压力值的效果明显不同。3 土体持水特性与细观组成的关系
3.1 不同干密度下试验分析

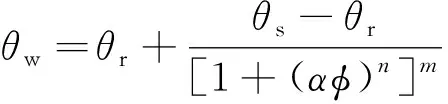



3.2 不同含水率下试验分析

4 结论

