基于改进的樽海鞘群算法求解机器人路径规划问题

刘景森 袁蒙蒙 李 煜

1(河南大学智能网络系统研究所 河南开封 475004) 2(河南大学软件学院 河南开封 475004) 3(郑州科技学院信息工程学院 郑州 450052) 4(河南大学管理科学与工程研究所 河南开封 475004)

近年来，移动机器人技术得到国内外普遍关注，它被认为是近百年来最重要的技术发明之一，对经济和社会发展具有重要意义.如今，移动机器人已涉及人类生活的各个领域，在工业、农业、服务业、太空探索、医疗康复等方面有着广泛应用.路径规划技术是移动机器人领域的关键、核心技术，它是机器人完成任务、抵达目标及智能化程度的重要标志，也是机器人导航中最重要的任务模块之一.路径规划问题是指基于某种优化策略和约束条件，在移动空间中寻找一条从起始点到目标点的最优或近似最优的安全路径，如何规划出能够平滑绕避障碍的高效路径是一个极具挑战性的研究课题.

国内外许多学者对这一领域不断进行研究，取得了较为丰硕的成果.提出和使用了A*算法[1]、栅格法[2]、人工势场[3]、可视图法[4]、Voronoi路线图搜索[5]、拓扑法[6]、模糊逻辑算法[7]、神经网络[8-9]、强化学习[10]、深度学习[11]等多种具有各自不同机制特点的规划技术及方法.虽然这些技术为求解移动机器人路径规划问题带来了可行有效的方法，但在实际规划中也都或多或少存在着一些较明显的缺点和不足.如：A*算法在求解大规模空间场景路径规划时，计算量和规划时间爆发性增加，所规划的路径中可能含有冗余点，估价函数也难于构造和选取.栅格法中算法性能过于依赖栅格划分粒度的大小，划分粒度小，则计算量和存储量急剧增加，环境干扰增强，栅格划分粒度大，则环境分辨率下降，难以规划出有效路径.人工势场法面对复杂障碍环境时引力势场较难规划，容易使机器人路径陷入停滞、抖动和局部最优，不适于进行大规模全局路径规划.可视图法灵活性较差，路径起始点或目标点一旦有变，可视图就要重新构建，而对于复杂环境中障碍物顶点较多时，规划时间也会急剧增加.Voronoi路线图搜索方法所规划的路径完整性和安全性较好，但最优路径质量和路径光滑性较差，而且路线图的绘制较为冗琐，难以应用到大规模场景规划中.拓扑法中拓扑网络的建立和更新都比较复杂，且拓扑图所包含的环境信息较少，难以识别和区分场景中存在的相似位置节点，对规划出的路径质量有不利影响.模糊逻辑算法的路径规划质量主要依赖于规则库，规则更新比较频繁，当输入输出量增长时，推理规则将会呈指数级增加.神经网络方法在求解复杂障碍环境时，需要的网络规模较大，而且各节点的阈值及之间的权值都在不断调整更新，对机器人的计算能力要求较高.强化学习方法不需先验知识，但要不断从环境中得到反馈，需要学习的参数较多，其路径规划质量取决于根据环境特征构建的模型，更适用于比较简单的结构化环境.深度学习方法是一类能提取数据中更高阶、更抽象隐藏特征的多层神经网络，在对复杂场景进行规划时计算量庞大、收敛较慢，同时处理空间不透明，决策性较差.因此，随着对移动机器人路径规划问题研究和应用的不断深入，规划场景的类型、规模和复杂程度不断变化和增加，移动机器人的有限资源能力和高实时性要求，使得这些算法在规划时间和路径结果上往往难以得到满意效果.最近几年，通过大量的研究和实验发现，元启发式智能优化算法在求解机器人路径规划方面具有独特优势，并且多种智能优化算法已经成功应用于路径规划的搜索策略中，如蚁群算法[12-14]、人工蜂群算法[15-16]、模拟退火算法[17]、遗传算法[18-20]、粒子群算法[21-22]等.但目前的应用还比较初期，使用的规划算法多为几个基础老算法，而对于当前智能计算领域中机制更优、能力更强、性能更好的新兴基础和改进算法研究很少，路径规划过程中也存在着一些各自的问题.如遗传算法对环境改变的适应性较差，搜索效率偏低；蚁群算法收敛速度较慢，有时会产生机器人停滞现象.故此，探索求解效率更高、环境适应性更好、寻优能力和鲁棒性更强的优化算法路径规划方案，是这一领域研究者们持续追求的目标和方向.

樽海鞘群算法(salp swarm algorithm, SSA)作为一种具有较高认可度和影响力的新型启发式智能优化算法，由Mirjalili等人[23]于2017年提出.SSA算法模拟了樽海鞘群体的链式觅食行为，机制清晰、参数简单、寻优性能优越，已成为智能计算领域广受关注和研究的重要算法，并在光伏系统优化[24]、图像处理[25]、生物医学信号处理[26]等诸多领域和问题的优化中得到成功应用.

但与此同时，SSA与其他元启发式群智能优化算法类似，存在着全局搜索能力有所不足、寻优质量不够稳定、有时易陷入局部极值等缺点，许多学者也针对这些问题提出了相应改进.Jia等人[27]在领导者和追随者位置更新公式中分别引入交叉策略和莱维飞行轨迹，提高了算法的收敛速度和收敛精度.王梦秋等人[28]在算法中增加了自适应评估移动、邻域最优引导以及反向学习扰动等策略，提高了樽海鞘群算法的寻优性能.Qais等人[29]基于高斯模型改进领导者公式中的参数，并在追随者更新公式中引入随机数，不但使算法更快收敛，而且增强了对高维函数的寻优能力，在变速风力发电机的应用中能够获得更高效率和更低成本.邢致恺等人[30]将莱维飞行机制应用于领导者位置更新，更好地平衡了算法的探索和挖掘能力，而后用改进算法进行图像分割，取得了不错结果.Ewees等人[31]将萤火虫算法与樽海鞘群算法相结合，增强了SSA算法在局部区域的挖掘能力，并成功应用于平行机最小化调度问题.

为了更好地求解机器人全局路径规划问题、提高樽海鞘群算法的寻优性能、扩展其应用范围，本文提出一种差异演化的寄生樽海鞘群算法(a parasitic salp swarm algorithm based on differential evolution, PDESSA).首先在领导者位置更新公式中引入上轮进化代对应领导者的位置信息，以增强算法的全局搜索继承性，提升对局部最优点和局部极值区域的摆脱能力；同时还在该全局搜索公式中增加了随进化代数自适应递减的惯性权重，更合理有效地平衡了算法的前期广泛探索和后期精细挖掘能力，提升求解性能和精度；最后将寄生-宿主双种群的寄生行为和优胜劣汰机制引入算法的演化结构和策略中，进一步增强了樽海鞘个体的多样性，提高了算法的搜索效率和摆脱局部极值能力.随后，基于算法流程伪代码和时间复杂度分析，证明了本文算法PDESSA与基本SSA算法时间复杂度相同.然后使用6种性能优越的代表性对比算法，在10个不同极值特征的标准测试函数上进行优化对比实验，对测试结果的统计分析表明，PDESSA的寻优精度、收敛性能和求解稳定性相比于对比算法均有显著优势.最后，把改进后算法PDESSA结合三次埃尔米特插值方法，定义基于路径上节点组合的个体编码方式，构建能避开所有障碍并实现最小路径的数学模型，进行机器人全局路径规划问题的优化求解.2种不同障碍环境下的路径规划算例求解实验和对比分析显示，融合三次埃尔米特差值的PDESSA算法对于解决机器人全局路径规划问题有着明显的可行性和有效性，与其他对比算法和插值方法相比优越性显而易见.

1 PDESSA算法

1.1 标准SSA算法

步骤1. 产生初始种群：

(1)

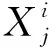
步骤2.计算种群中每个樽海鞘个体的目标函数值，并依据此适应度值将种群个体排序，适应度值最优的个体所在位置便是初始食物源.

步骤3.种群中前1/2个体称为领导者，后1/2称为追随者.

步骤4.对樽海鞘领导者进行位置更新：

(2)

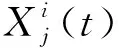
c1=2e-(4t/Max_iter)2,

(3)

其中，Max_iter为最大进化代数.

步骤5.对樽海鞘追随者进行位置更新：

(4)

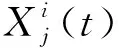
步骤6.对于更新后的樽海鞘个体进行逐维边界处理，用各维边界值替代个体在对应维度上的越界值，比较替换得到新的当前全局最优位置，并用其刷新食物源坐标.

步骤7.判断迭代次数是否已达到最大进化代数.若是，就输出得到的全局最优结果；若否，则转回步骤3继续执行寻优迭代过程.

1.2 改进领导者全局搜索方式

1.2.1 上代领导者位置信息的影响

在标准SSA的整个迭代过程中，占种群个体数量1/2的领导者，都是直接奔向当前全局最优解位置(食物源)的，这种位置更新方式会导致算法搜索过程中跳跃性过强，执行全局搜索的领导者多样性较低，难以保证全局空间中搜索的充分性和完备性，易早熟收敛和滞困于局部最优.针对这一问题，本文将上轮迭代中对应的领导者信息引入领导者更新公式，使领导者既受到全局最优解的影响，又与上轮进化结果相关联，既分享了整个樽海鞘群的全局进化成果，也保留了每个领导者的个体进化印记，从而提升了算法跳出局部极值区域找到全局最优的能力.改进事后的领导者位置更新：

(5)

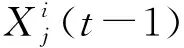
1.2.2 非线性惯性权重

本文还在领导者位置更新公式中增加了自适应惯性权重w，权重值的大小控制着当前全局最优位置(食物源)对领导者位置更新的影响，从而决定了领导者的全局搜索能力.w的值随着进化代数的递增呈非线性递减趋势，迭代前期w比较大，领导者受食物源位置影响较强，从上代位置向较大空间范围广度搜索，而进化后期领导者已搜索至全局最优区域，此时较小的w取值能使领导者在上轮进化到达的位置附近精细挖掘，增强了算法全局和局部搜索的平衡性，提高了寻优能力和求解精度.w计算为

(6)

结合式(5)(6)，新的樽海鞘领导者位置更新：

(7)

其中，w的取值随进化代数的不断增加以双曲正切函数的方式非线性减小，其值域为(0,1).自适应权重的使用，更好地平衡了算法在不同进化阶段对领导者搜索能力的不同需求，使它们更有效、更合理地发挥领导作用，增强算法寻得全局最优解的可能和能力.

1.3 寄生和宿主双种群

寄生是一种生物(寄生者)生活在其他生物(宿主)体表或体内，并从宿主中吸取营养以维持寄生者生存需要的现象.寄生者是生物界一种非常普遍的存在，如病毒、细菌、真菌等.依据寄生程度不同，可将寄生现象分为离开寄生无法独立生活的专性寄生、既可寄生也可独立生活的兼性寄生2种.

受寄生现象启发，本文提出一种拥有双种群及2套进化机制的改进算法结构，在算法演化过程中始终维持着宿主和寄生2个种群，每个种群的个体数量均为N.两者的进化策略不同，独立演化，其中宿主群使用标准SSA的位置更新公式，而寄生群则使用1.2节改进后的领导者更新方式.每隔一定进化代数M，就发生一次寄生群从宿主群吸收营养的寄生行为，即寄生群用P个适应度值最差的个体置换宿主群中前P个适应度值最好的个体.P是每次寄生行为的个体置换数，取值随进化代数的增加自适应减小：

P=round(((Max_iter-t)/Max_iter)×N/4)，

(8)

其中，round()是四舍五入函数，用来对置换个数取整.随着进化代数不断增加，寄生行为也在不断发生，宿主群中位置较优的个体(营养)不断被寄生群吸走，寄生群已经得到了较多营养，因此交换个数也在不断递减，直到进化终止，寄生行为也随之彻底结束.

为了保持宿主种群的个体质量和活跃性，每一次寄生行为后还要对宿主种群中一定比例的Q个较差樽海鞘进行随机淘汰，替换以搜索空间中产生的随机个体Q:

Q=round((0.5+rand()/2)×N/4).

(9)

宿主群进行优胜劣汰的步骤为：

fori=1:Q

ifrand()>0.5

淘汰替换当前个体;

end if

end for

通过对宿主种群中最差的Q个樽海鞘个体实行随机劣汰，有效提升了宿主群的个体质量和多样性，降低了算法陷入局部极值的可能性.同时这一策略也很好地契合了自然进化和优化搜索机制中的优胜劣汰思想，较好地解决了由于宿主群中高质量樽海鞘个体持续流失减少而导致种群活跃度较低、易陷入低效搜索的问题.

2 PDESSA的流程与时间复杂度

2.1 PDESSA流程伪代码

算法1.PDESSA.

begin

设置算法中基本参数的初值;

计算寄生群和宿主群中樽海鞘个体的初始位置;

计算2个种群中个体的适应度值;

设置宿主群、寄生群的食物源位置;

while (t≤Max_iter)

由式(6)计算w;

fori=1 toN

if (i≤N/2)

forj=1 toD

由式(7)对寄生群中的领导者进行位置更新;

end for

else

由式(4)对寄生群中的追随者进行位置更新；

end if

end for

fori=1 toN

if (i≤N/2)

forj=1 toD

由式(2)更新宿主群的领导者位置;

end for

else

由式(4)更新宿主群的追随者位置;

end if

end for

if mod (t,M)==0

由式(8)执行寄生行为;

由式(9)计算优胜劣汰个体数Q;

对宿主群中Q个较差个体进行随机劣汰替换;

end if

fori=1 toN

对2个种群更新后的樽海鞘个体进行边界

处理;

计算宿主群、寄生群中个体的适应度值;

对宿主群、寄生群的食物源位置进行更新;

end for

t=t+1

end while

end

2.2 PDESSA时间复杂度分析

评价一个优化算法的优劣需要兼顾寻优性能和时间复杂度，时间复杂度是考量和评估算法运行效率的重要指标.下面对PDESSA的时间复杂度进行分析.

在文献[32-33]中,我们都对标准SSA的时间复杂度做了详细分析.设算法的总迭代次数为Max_iter，种群规模为N，个体维度为n.

在SSA算法的初始化阶段，设初始化基本参数的时间为η0，产生个体位置中每一维初值的均匀分布随机数的时间为η1，由目标函数计算每个个体适应度值的时间为f(n)，根据适应度值对种群个体进行排序并由此找到初始代全局最优个体(食物源位置)的时间为η2，则这一阶段的时间复杂度为

T1=O(η0+N(nη1+f(n))+η2)=O(n+f(n)).

进入迭代循环，总迭代次数为Max_iter.

算法中樽海鞘领导者的数量为N/2.在更新领导者位置阶段，c1的值在同轮迭代中保持不变，c2和c3则是随个体和维度的变化而改变，设由式(3)求c1的时间为η3，c2和c3是均匀分布随机数，其生成时间均同η1.在式(2)中，2种公式的计算时间完全一致，由式(2)更新每个个体每维位置的时间为η4，则该阶段的时间复杂度为

T2=O(η3+(N/2)n(η1+η1+η4))=O(n).

算法中樽海鞘追随者数量是其余的N/2.在追随者位置更新阶段，设由式(4)对每个追随者位置进行更新的时间为η5，则此阶段的时间复杂度为

T3=O((N/2)η5).

在边界处理和更新食物源阶段，设每一个体做边界处理的时间为η6，求个体适应度值的时间仍为f(n),按适应度值与食物源位置进行比较替换的时间为η7，则这一阶段的时间复杂度为

T4=O(N(η6+f(n)+η7))=O(f(n)).

因此标准SSA的总时间复杂度为

T(n)=T1+Max_iter(T2+T3+T4)=O(n+f(n)).

在本文提出的PDESSA算法中，种群的规模、个体维数、初始化基本参数的时间、产生一个均匀分布随机数的时间、计算目标函数适应度值的时间、按个体适应度值对种群中个体排序并得到当前最优位置(食物源)的时间均与标准SSA相同.由于PDESSA中包含寄生群和宿主群2个种群，因此PDESSA在初始化阶段的时间复杂度为

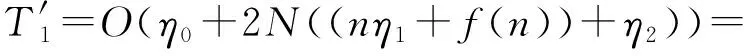
进入迭代循环，总迭代次数为Max_iter.

算法中寄生、宿主2个种群的领导者数量均为N/2，而追随者数量则为各自种群中剩余的N/2.

对于寄生群，设由式(6)求w的时间为t1，其值在同轮迭代中保持不变.在寄生群领导者位置更新阶段，设由式(7)更新每个领导者位置中每一维度的时间为t2，则这一阶段的时间复杂度为

在寄生群追随者位置更新阶段，由式(4)更新每个追随者位置的时间与标准SSA相同，则这一阶段的时间复杂度为

对于宿主群，所有个体(领导者、追随者)的位置更新都分别与标准SSA相同，执行这些操作所花费的时间也相同，故而该阶段的时间复杂度为

在寄生行为和宿主群优胜劣汰阶段，设计算个体适应度值的时间为f(n)，按适应度值对樽海鞘个体进行排序的时间为t4，此时种群数为2，故执行寄生行为和宿主群优胜劣汰2步操作的总个体数为基本算法的2倍.设由式(8)计算寄生行为个体交换量P的时间为t5,交换寄生群和宿主群中P个个体的时间为t6，由式(9)计算宿主群中劣汰率Q的时间为t7，随机新个体并替换劣质旧个体的时间为t8，则在2个种群间发生一次寄生并对宿主种群进行一次劣汰的时间为

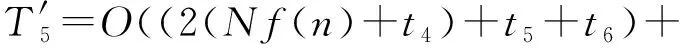
在边界处理和食物源更新阶段，对每个个体进行边界处理、由目标函数计算个体适应度值、按个体适应度值比较替换全局最优解位置(食物源)的时间都与标准SSA相同，而且对寄生群和宿主群的处理完全一致，因此该阶段的时间复杂度为

由此得出，PDESSA算法总的时间复杂度为

与标准SSA相比，本文算法PDESSA的执行时间有所增长，但时间复杂度保持不变，PDESSA的机制改进没有降低算法的运行效率.

3 PDESSA函数优化仿真实验

为测试本文算法PDESSA的优化性能，使用10个具有不同极值特征的复杂标准测试函数，将本文提出的PDESSA算法与基本樽海鞘群算法(SSA)、改进樽海鞘群算法(ISSA)[28]、基于莱维飞行的樽海鞘群算法(LSSA)[30]、标准粒子群算法(PSO)[34]和PPSO(phasor particle swarm optimization)[35]共6种算法，分别在30维和100维上进行对比测试.其中，ISSA和LSSA算法是2个代表性SSA改进算法；PSO是求解机器人路径规划问题最常用和性能优越的群智能算法之一；PPSO是一种新的PSO改进算法，有效提高了PSO算法的收敛性和鲁棒性.所有6种算法均在相同软、硬件条件下独立运行，环境为Windows8、处理器Intel i5-3337@1.8 GHz，内存为4 GB，编程环境为Matlab R2014a.算法参数方面，4种樽海鞘算法无需另外设置参数，而PSO，PPSO算法的惯性权重w=0.8，学习因子c1和c2均为1.5，都与各自算法的原文献和源代码保持一致.

3.1 测试函数

本文使用的10个不同寻优特性的典型复杂标准测试函数如表1所示.其中f1(x)～f2(x)为多维单峰函数，这类函数只有一个全局最优值，没有局部极值，常用于验证算法的收敛速度与求解精度；f3(x)～f10(x)为多维多峰函数，这类函数不仅具有大量的局部极值，而且最好的局部极值点与全局最优点距离较远，主要用来测试算法摆脱局部极值的能力及全局、局部搜索的平衡性.

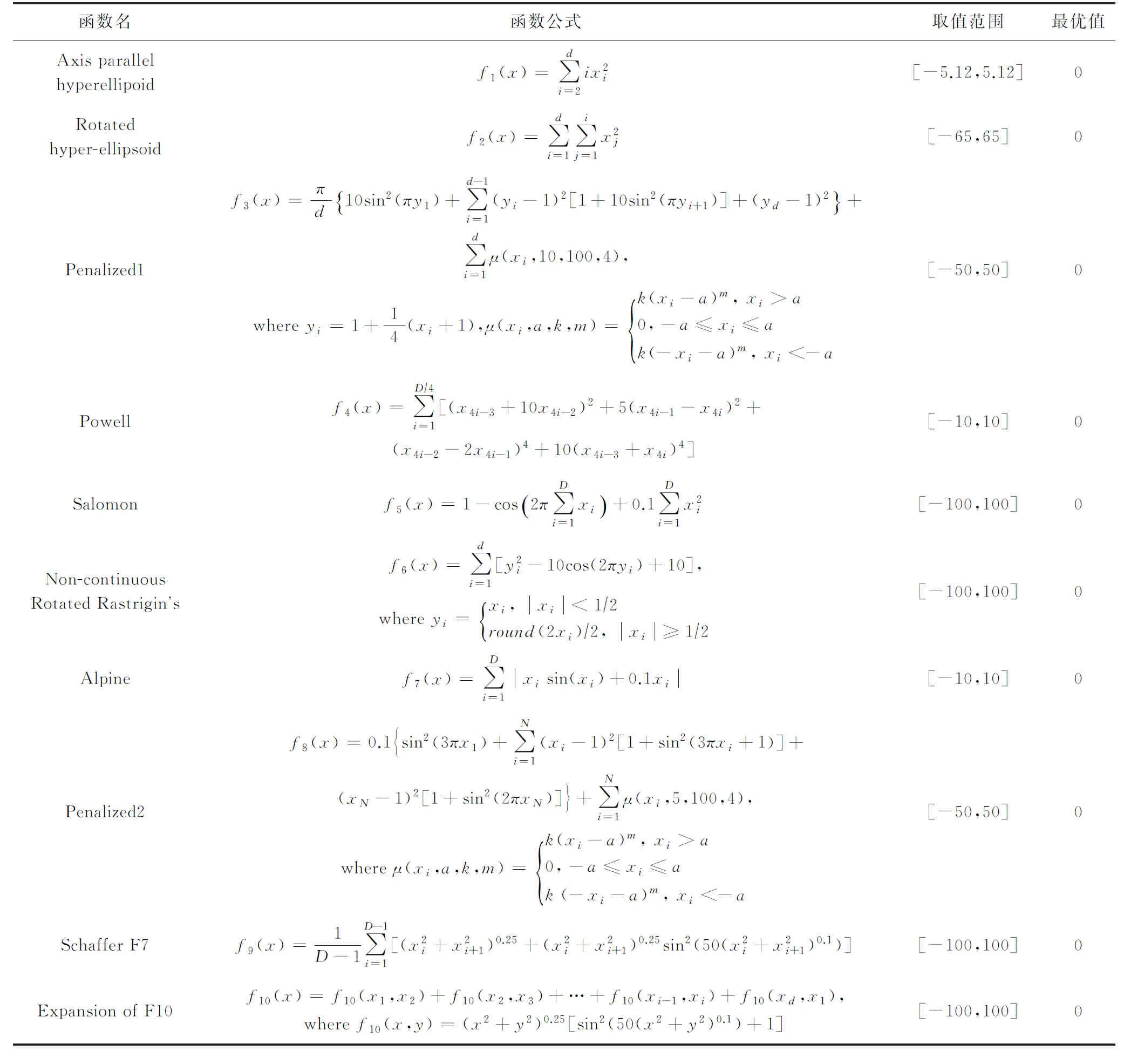
Table 1 Test Function表1 测试函数

3.2 寻优精度分析

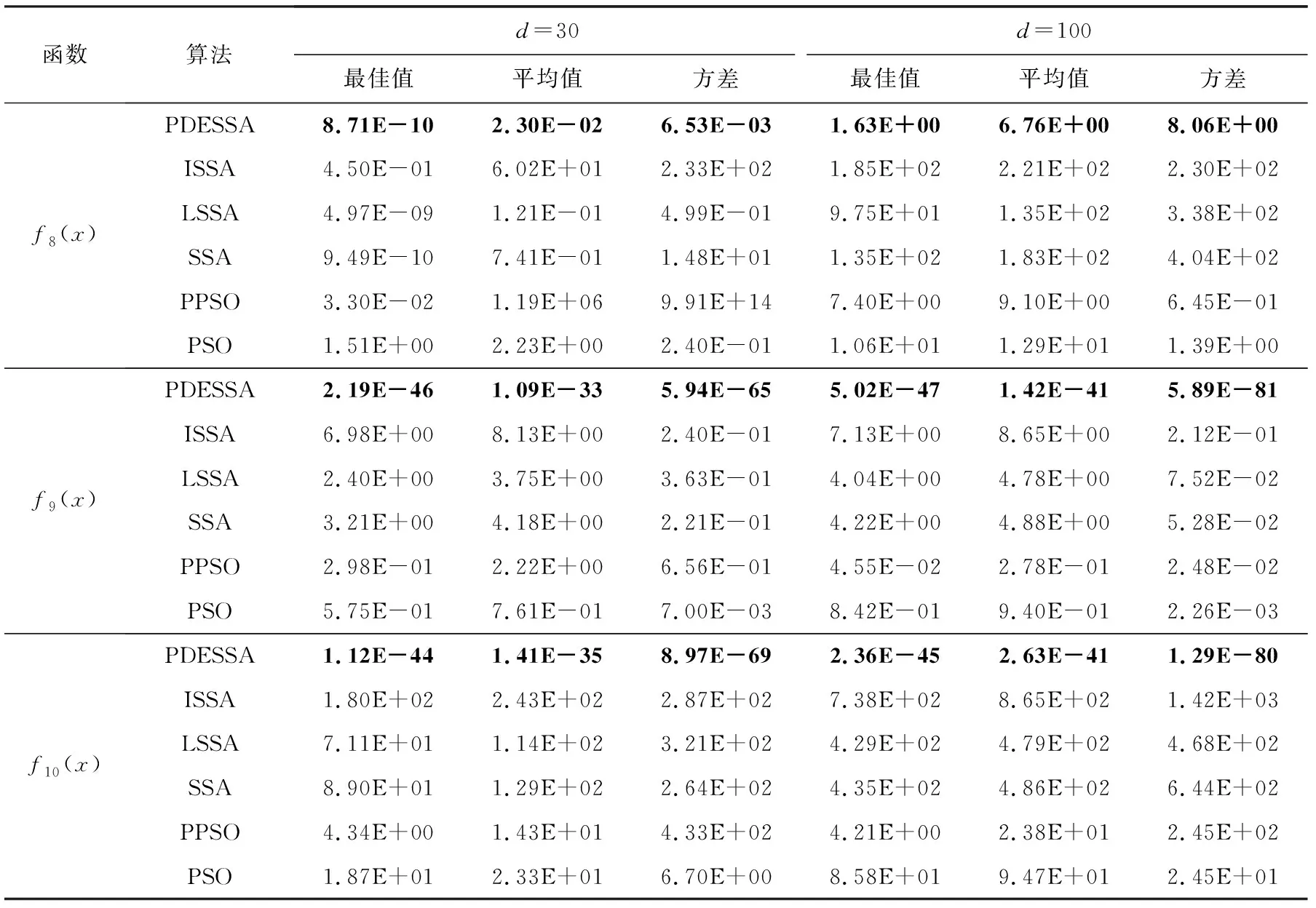
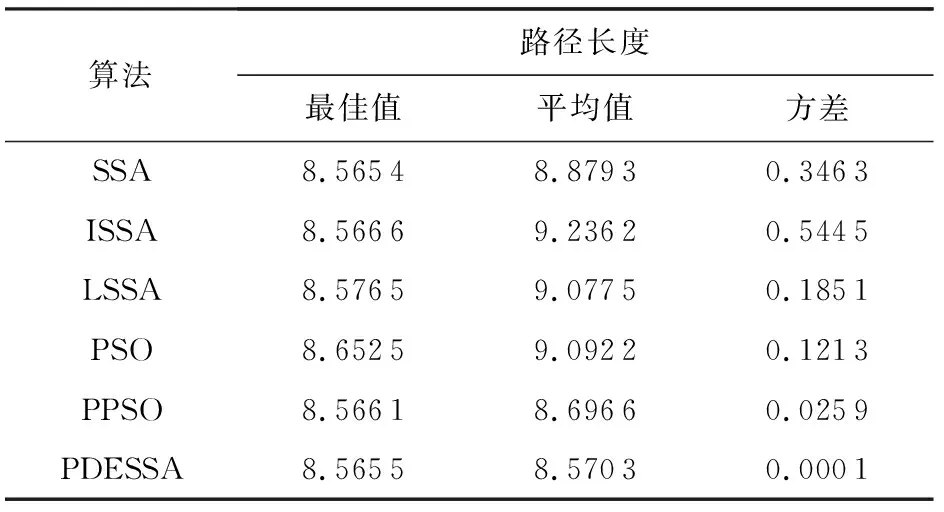
为测试和检验PDESSA的寻优性能，将f1(x)～f10(x)的维度分别设置为d=30,100进行极值优化实验.基于测试的客观性和充分性，各算法在相同环境下独立运行50次，种群规模N=30，最大进化代数Max_iter=1 000.表2统计了30维和100维下各算法运行50次得到的寻优结果的最佳值、平均值和方差，其中各项对应的最优值均做了加粗显示.

观察表2可以看出，除了很少数的个别情况外，PDESSA算法求解不同维度下各个函数的寻优精度和稳定性都明显优于其他5种对比算法，且在全部10个测试函数的所有维度上，50次寻优结果的最佳值、平均值和方差皆优于基本SSA算法，显示出本文算法对于SSA机制改进的显著性和有效性.

在30维条件下，对于2个复杂单峰函数f1(x)～f2(x)，PDESSA的最佳值、平均值和方差都明显优于其他5种对比算法，求解优势突出.对于8个复杂多峰函数f3(x)～f10(x)，PDESSA的最佳值、平均值和方差也全部优于其余5种算法，尤其是对于函数f6(x)，PDESSA的最佳值、平均值和方差均为理论最优值，求解能力十分出色.

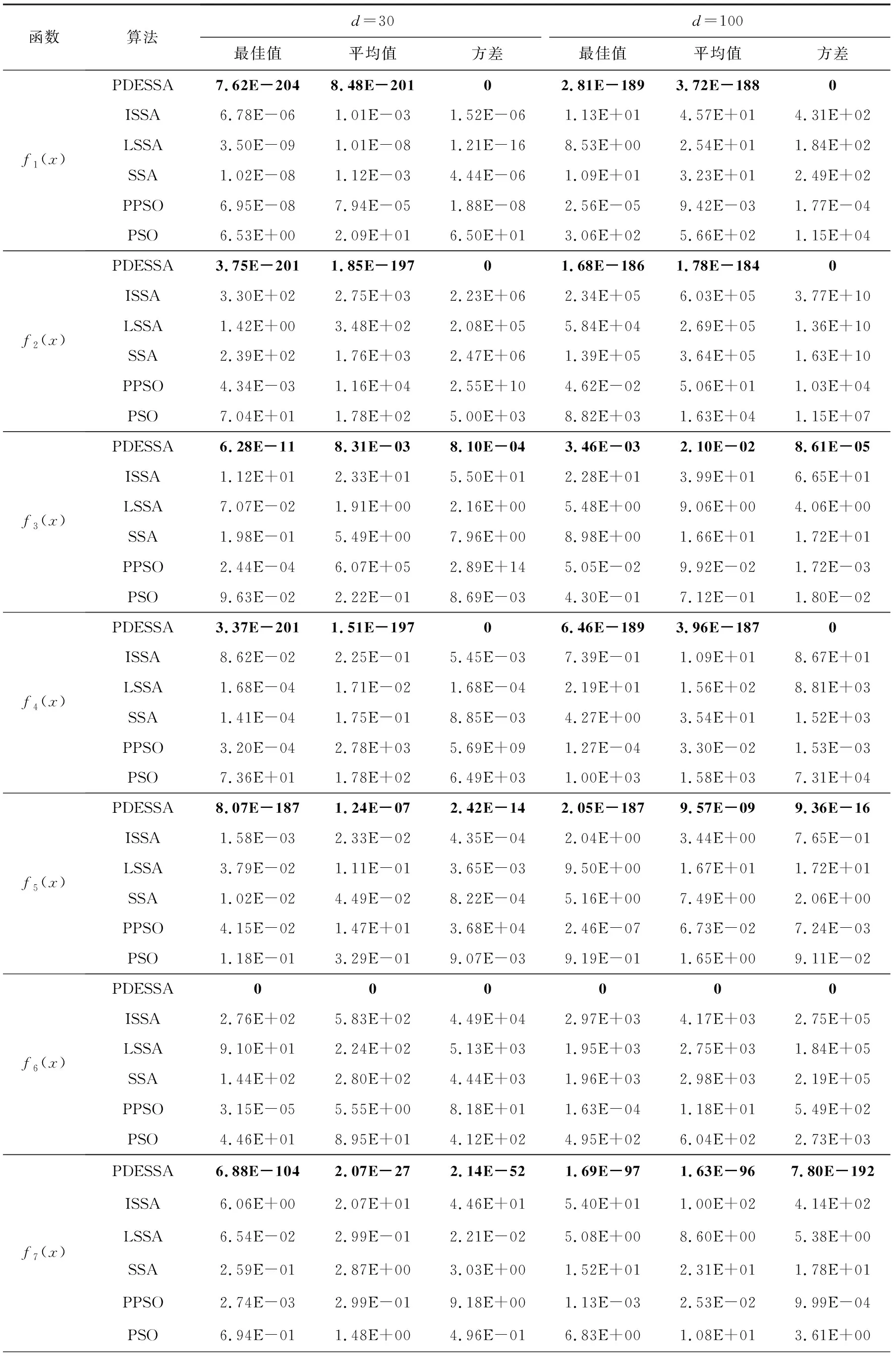
Table 2 Comparison of Optimization Results of 6 Algorithms Under Fixed Iteration Times表2 6种算法在固定迭代次数下的寻优结果比较

续表2

在100维条件下，由于维数增加6种算法的寻优精度都会有所下降，但PDESSA仍然表现出优越的求解能力和维度适应性，寻优结果受维数变化影响较小，寻优精度优于其他5种算法.对于2个单峰函数f1(x)～f2(x)，PDESSA的最佳值、平均值和方差都远优于其他5种算法，求解能力依然出色.对于多峰函数f3(x)～f7(x)和f9(x)～f10(x)，PDESSA在这7个函数上得到的最佳值、平均值和方差都优于其他5种算法，特别是对于函数f6(x)，PDESSA寻优结果的最佳值、平均值和方差仍是理论最优值，求解效果优越且稳定.对于函数f8(x)，PDESSA的方差略逊于PPSO算法但优于其余4种算法，而最佳值和平均值则都是6种算法中最好的.

以上求解结果和分析表明，无论是单峰、多峰还是低维、高维，相比于5种求解性能较为优越的代表性对比算法，本文算法PDESSA整体呈现出较好的寻优性能，求解精度和稳定性更加出色，很好地解决了SSA算法在求解复杂函数全局优化时易陷入局部极值、寻优性能不稳定、求解精度有时不高的问题.

3.3 收敛曲线分析

一个算法的收敛曲线显示了该算法在寻优过程中收敛速度的变化及陷入局部极值的次数，通过收敛曲线可以直观地展现和对比出算法寻优性能的优劣.图1～10给出了6种算法在d=100维时，求解10个复杂标准测试函数f1(x)～f10(x)的收敛曲线对比图.

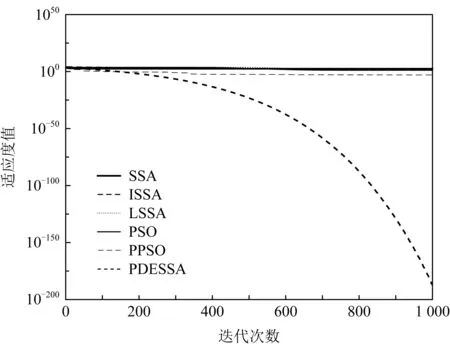
Fig. 1 Convergence curve of f1(x) function图1 f1(x)函数的收敛曲线

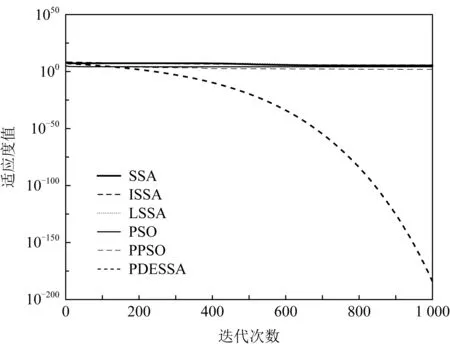
Fig. 2 Convergence curve of f2(x) function图2 f2(x)函数的收敛曲线

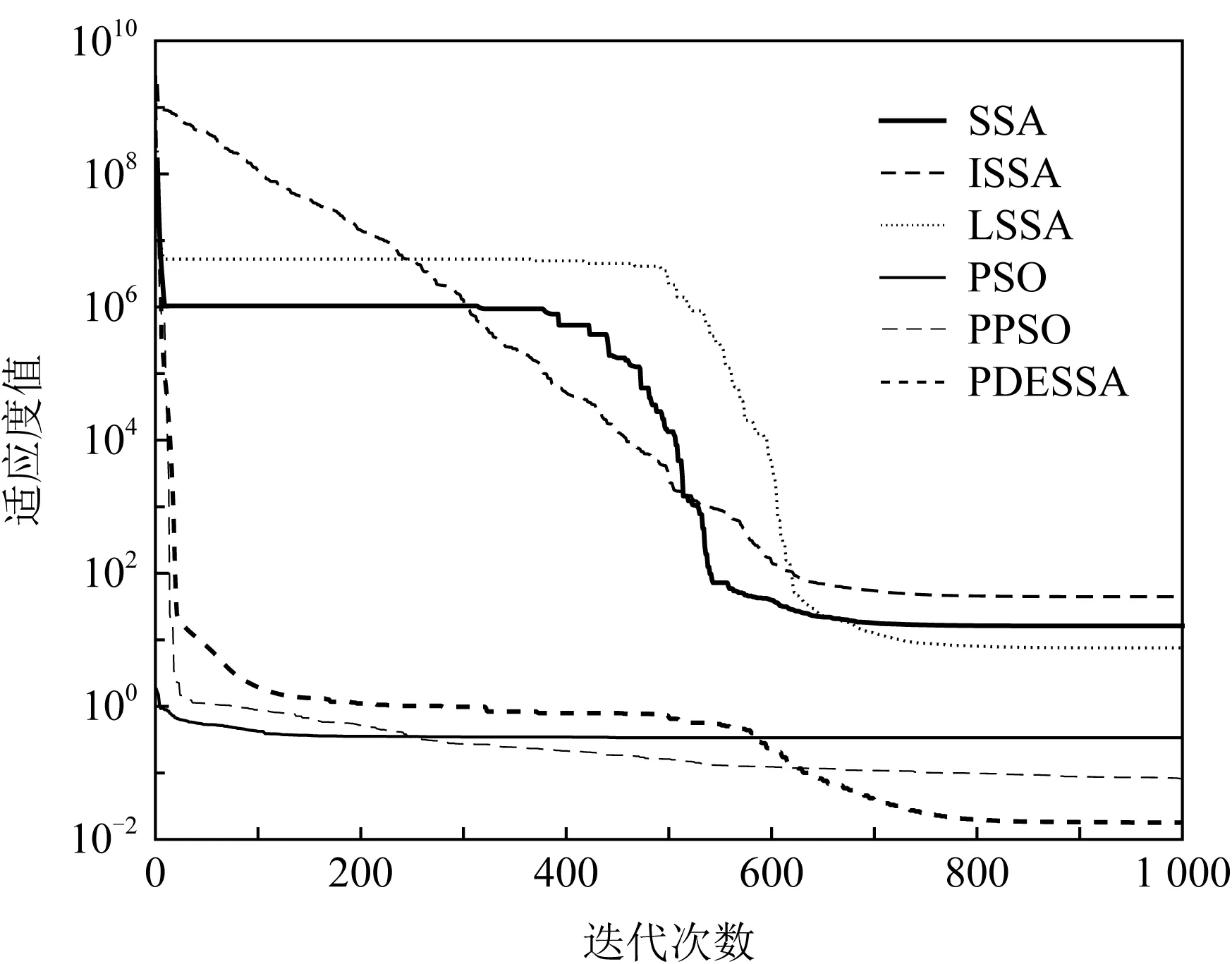
Fig. 3 Convergence curve of f3(x) function图3 f3(x)函数的收敛曲线

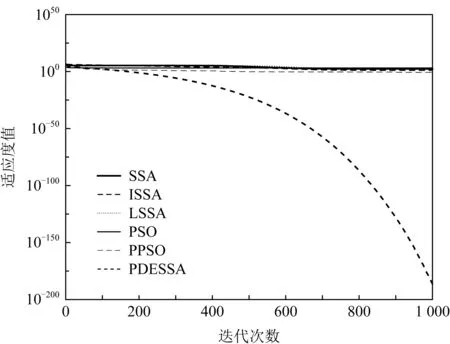
Fig. 4 Convergence curve of f4(x) function图4 f4(x)函数的收敛曲线

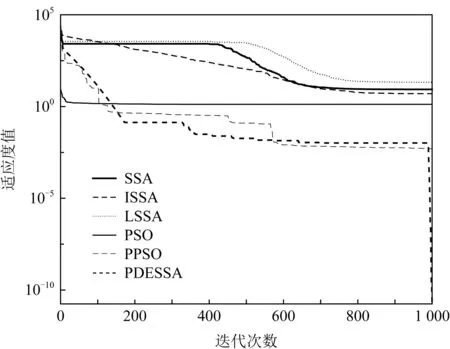
Fig.5 Convergence curve of f5(x) function图5 f5(x)函数的收敛曲线

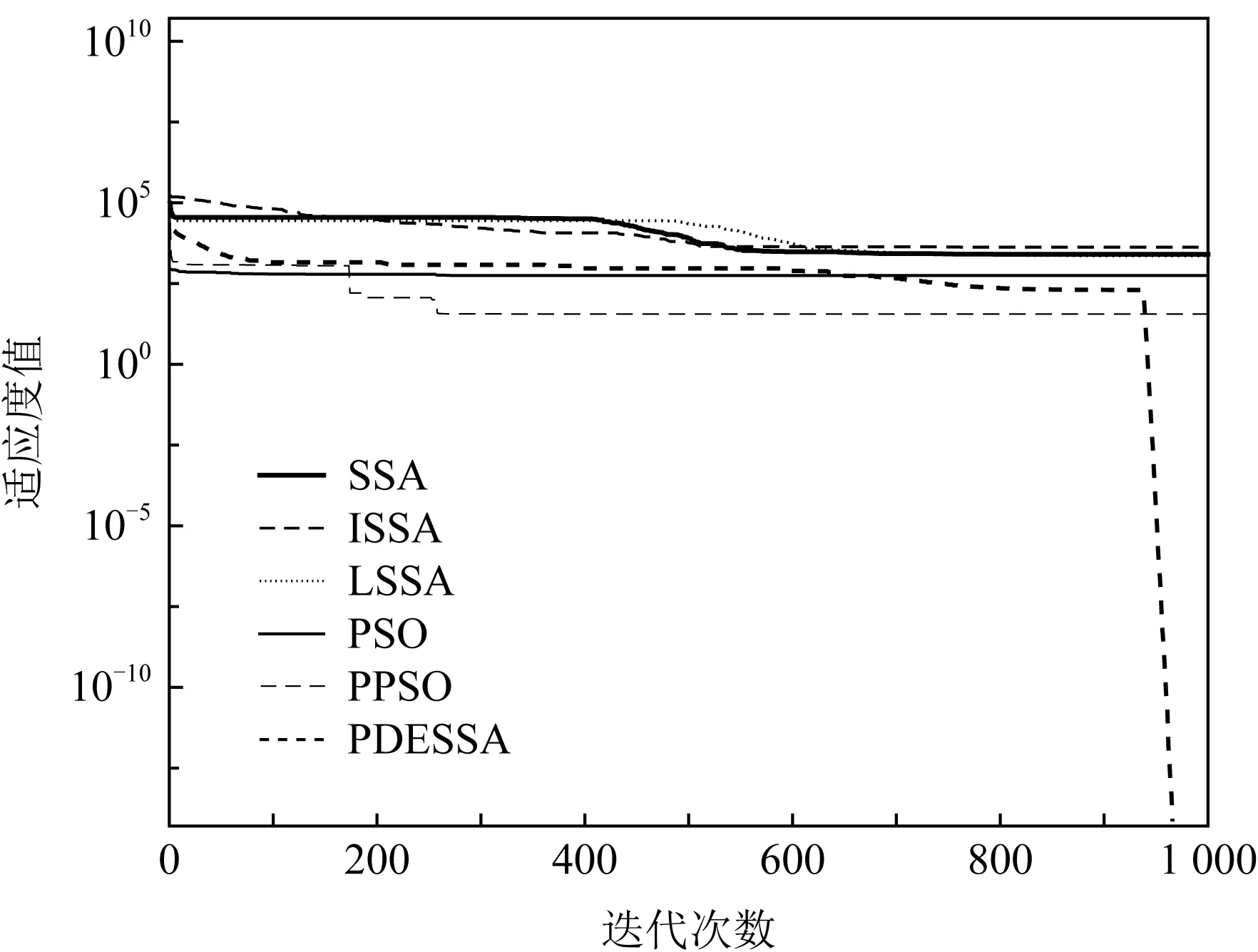
Fig. 6 Convergence curve of f6(x) function图6 f6(x)函数的收敛曲线

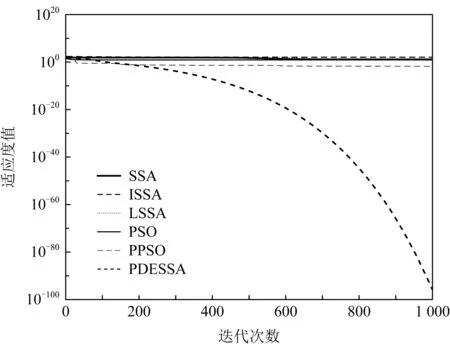
Fig. 7 Convergence curve of f7(x) function图7 f7(x)函数的收敛曲线

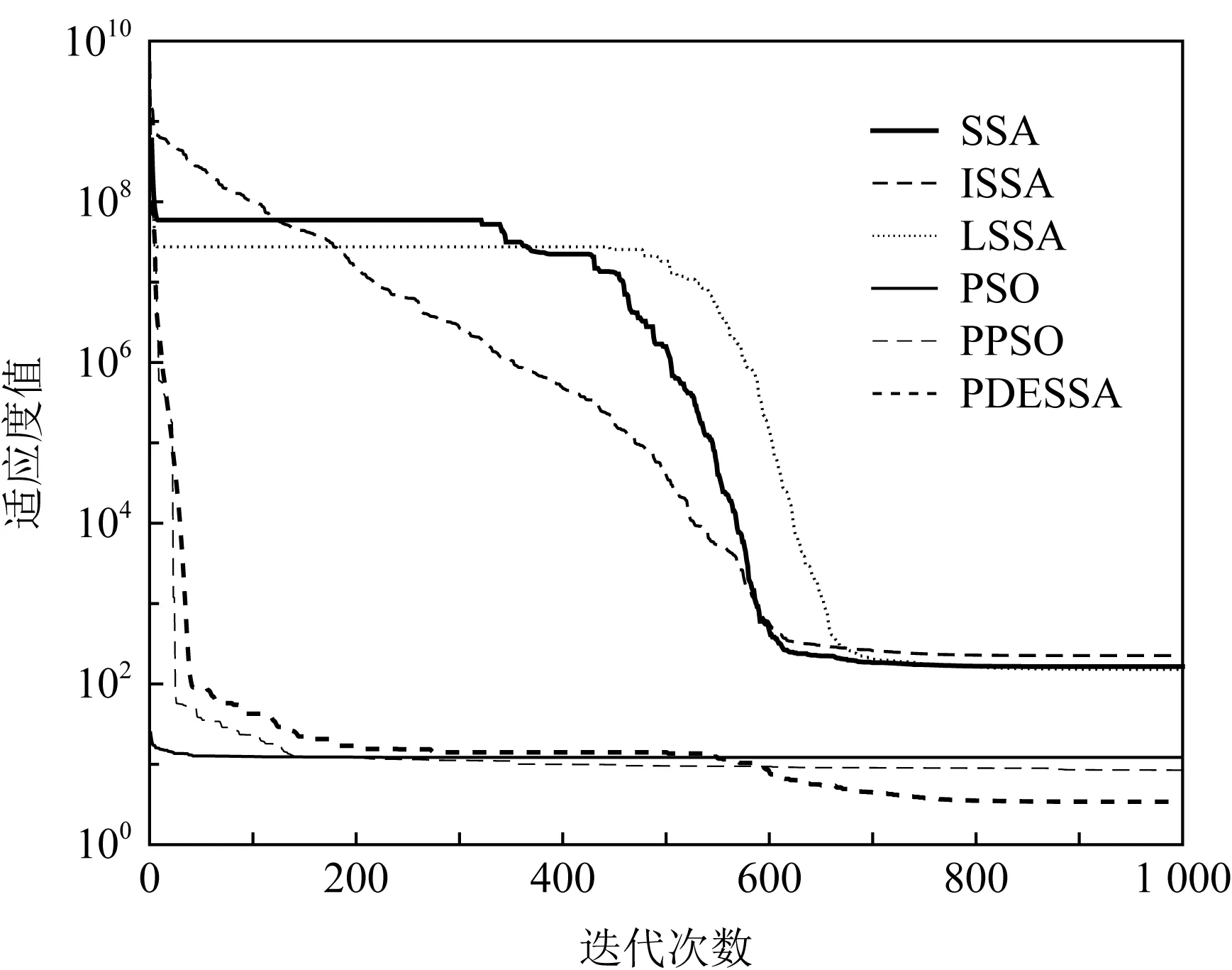
Fig. 8 Convergence curve of f8(x) function图8 f8(x)函数的收敛曲线

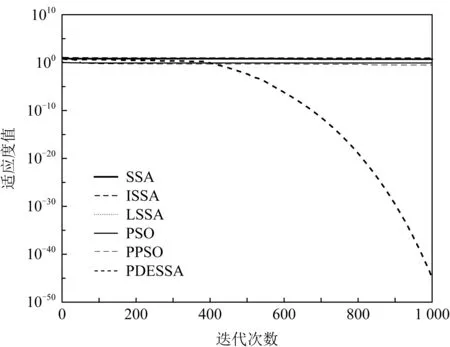
Fig. 9 Convergence curve of f9(x) function图9 f9(x)函数的收敛曲线

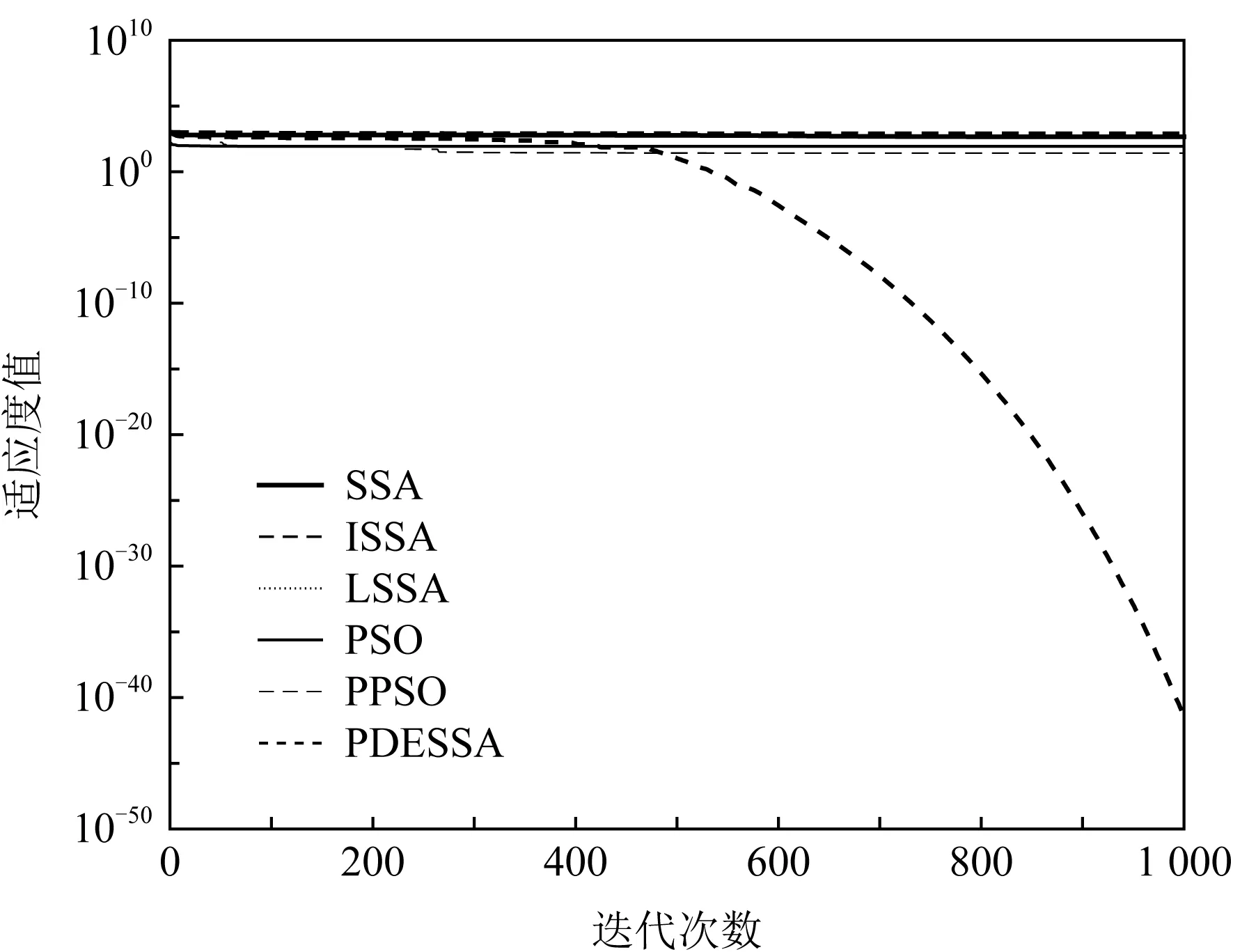
Fig. 10 Convergence curve of f10(x) function图10 f10(x)函数的收敛曲线

图1～10清晰展现出PDESSA及5种对比算法在整个迭代过程中当前最优适应度值的变化趋势对比.可以看出，相较于其他5种算法，PDESSA的收敛速度更快，收敛曲线总体比较光滑，陷入局部极值的次数少，寻优能力更强.

在求解高维复杂单峰函数时，对于图1和图2，SSA，ISSA，LSSA，PSO和PPSO算法从迭代开始曲线的下降就极其缓慢，收敛基本陷于停滞状态；而PDESSA算法从迭代开始到结束，始终保持较快下降趋势，最终收敛于理论最优值附近.

在求解高维复杂多峰函数时，对于图3和图8，SSA，ISSA和LSSA算法从迭代开始到结束收敛速度一直很慢，PSO和PPSO算法前期收敛速度略快于PDESSA，但600代后收敛速度已全部慢于PDESSA算法.对于图4和图7，PDESSA算法从迭代开始到结束都以很快的速度收敛，而其他5种算法从迭代进化的早期便陷于局部极值中无法摆脱.对于图5，PDESSA在进化前期也曾落入局部最优，但随着迭代的不断进行能在后期成功摆脱，并以较快速度收敛到全局最优解附近；而SSA，ISSA和LSSA算法的收敛速度始终很慢；PSO算法的收敛速度虽然在进化早期快于PDESSA，但100代时陷入局部极值无法跳出；PPSO算法在迭代前期收敛速度略快于PDESSA，但在100代之后就明显慢于PDESSA算法，到500代时更是陷入局部极值无法跳出.对于图6，PSO算法在进化初期便早早落困于局部最优无法摆脱；而PPSO，SSA，ISSA，LSSA算法的收敛速度则一直很慢，未能收敛到全局最优解；PDESSA前期虽然也曾受困于局部最优，但后期不但可以成功脱离，而且还能以较快速度收敛至理论最优解.对于图9和图10，PDESSA进化初期同样困滞于局部最优，但400代时成功摆脱，并以较快速度收敛，直至迭代结束到达全局最优解附近，而其他5种算法则是从迭代初期就陷入局部极值无法跳出.

由实验结果和分析可知，本文提出的PDESSA算法具有较为出色的优化性能，其寻优精度、收敛速度、求解结果的稳定性都优于其他5种性能优越的代表性对比算法.

4 PDESSA算法与三次埃尔米特插值方法相结合求解机器人路径规划问题

4.1 三次埃尔米特插值方法

在求解插值问题时，为构建更贴近契合于原函数的插值函数，我们要求在节点处，不仅原函数和插值多项式的函数值相同，两者的一阶或更高阶导数值也相同，这种插值就是埃尔米特插值方法，其插值多项式称为埃尔米特插值多项式.

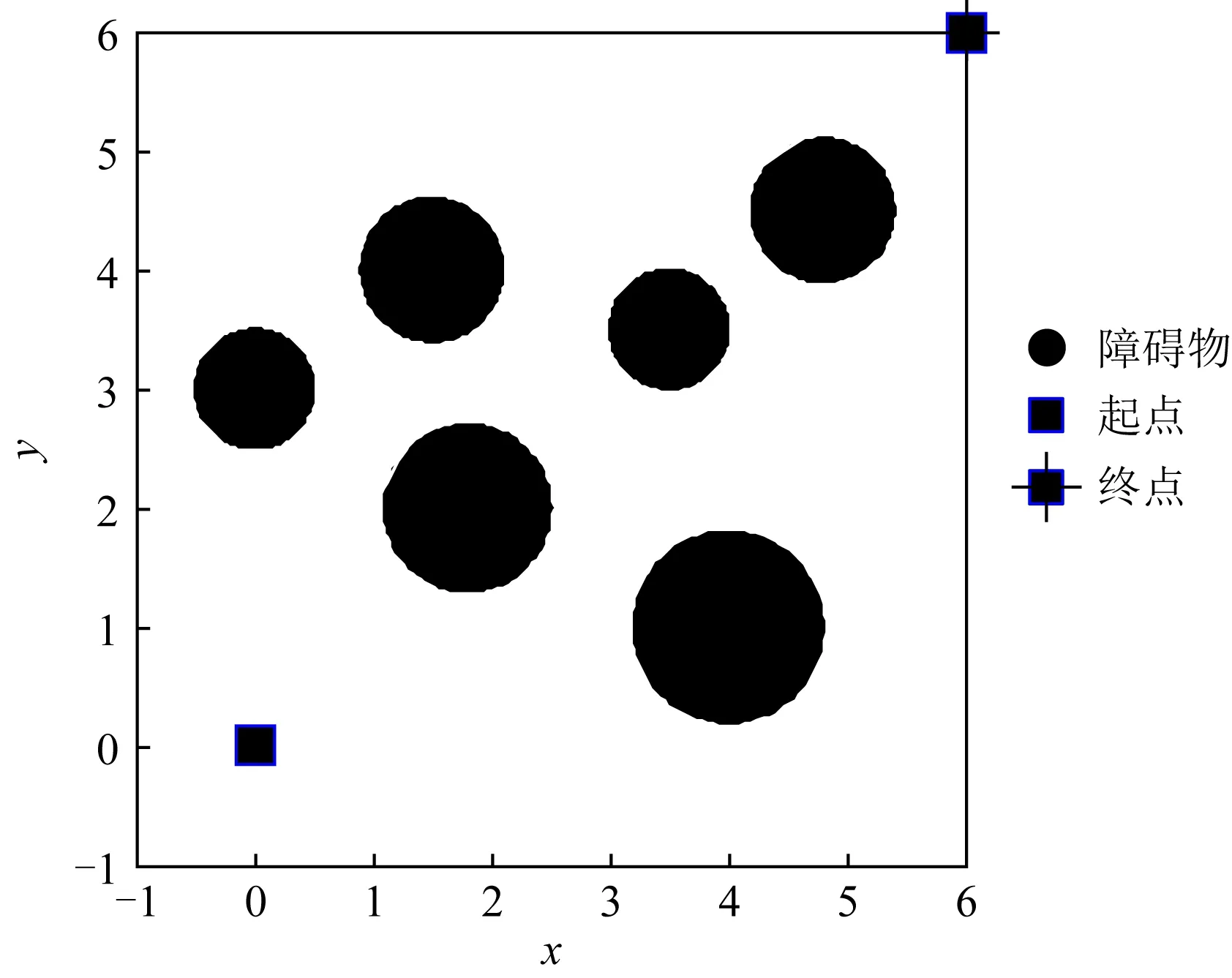
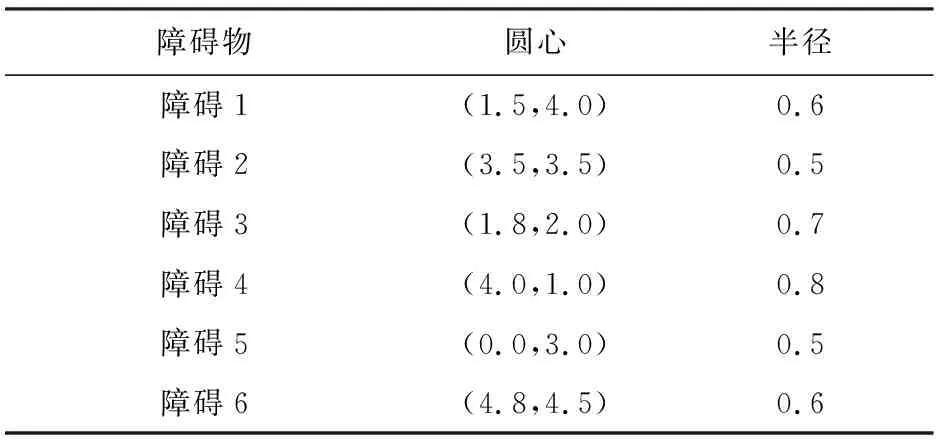
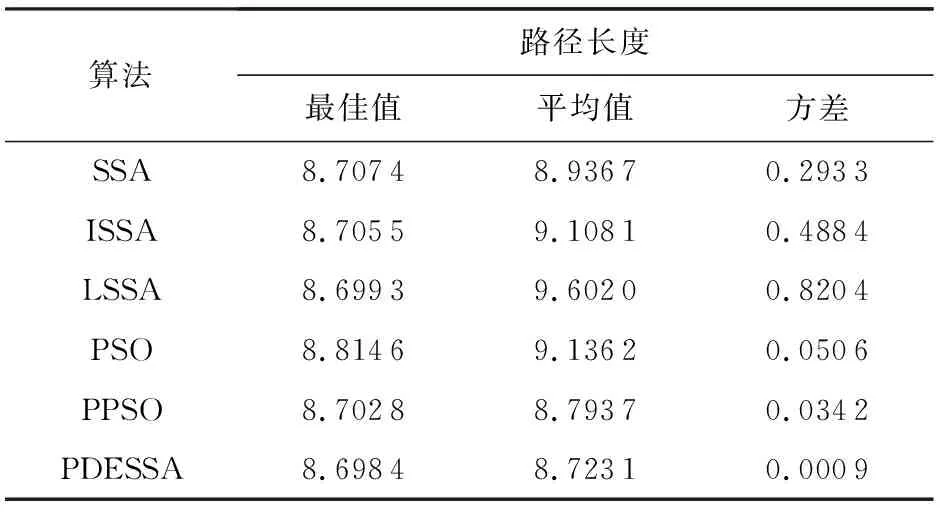
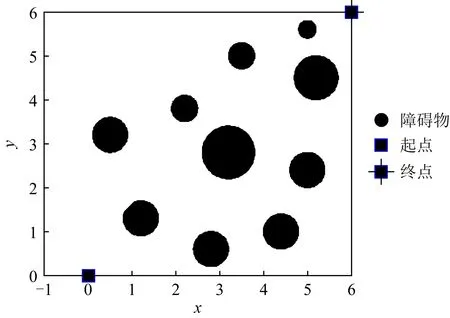
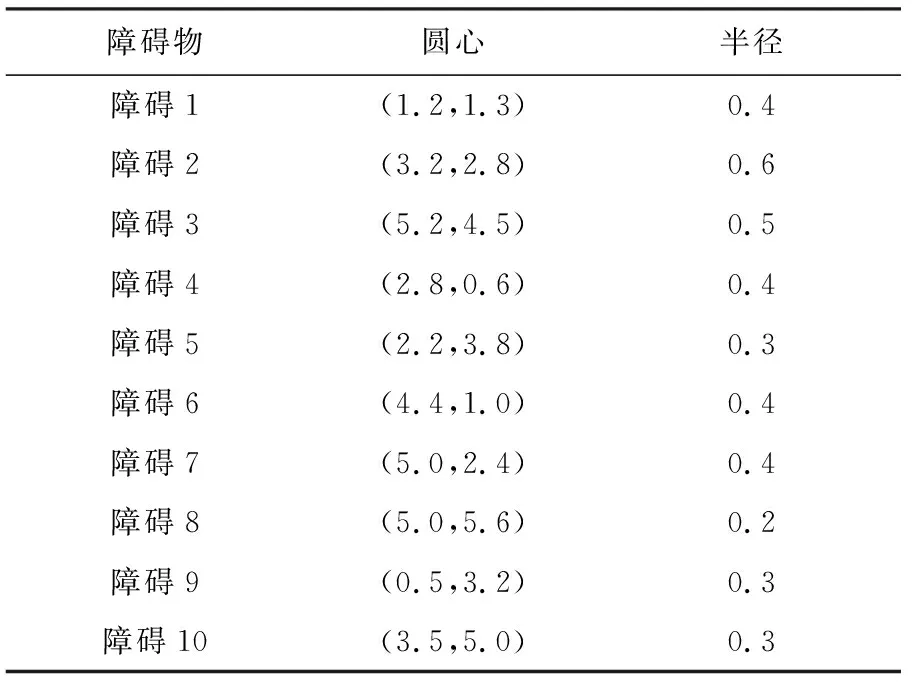
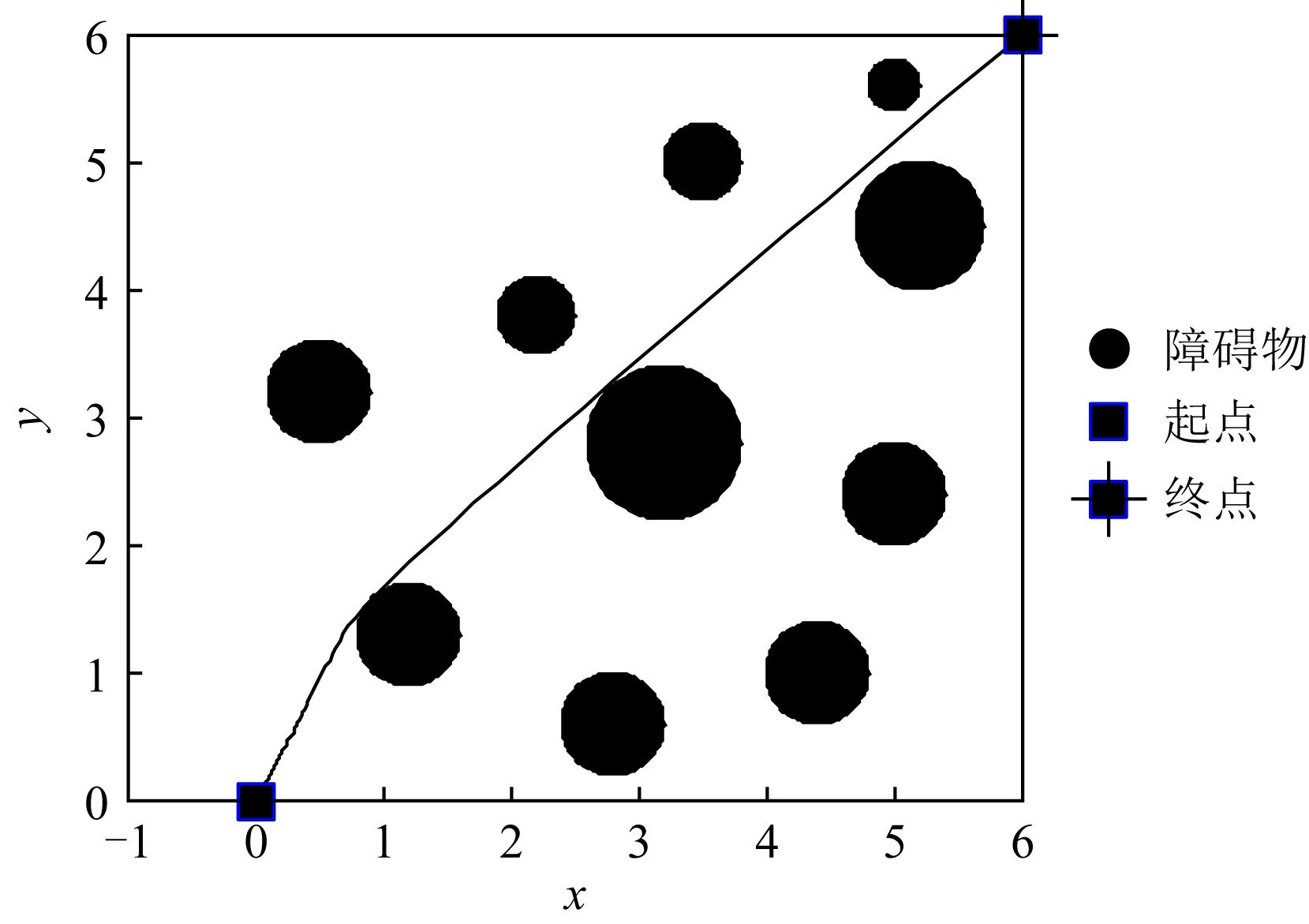
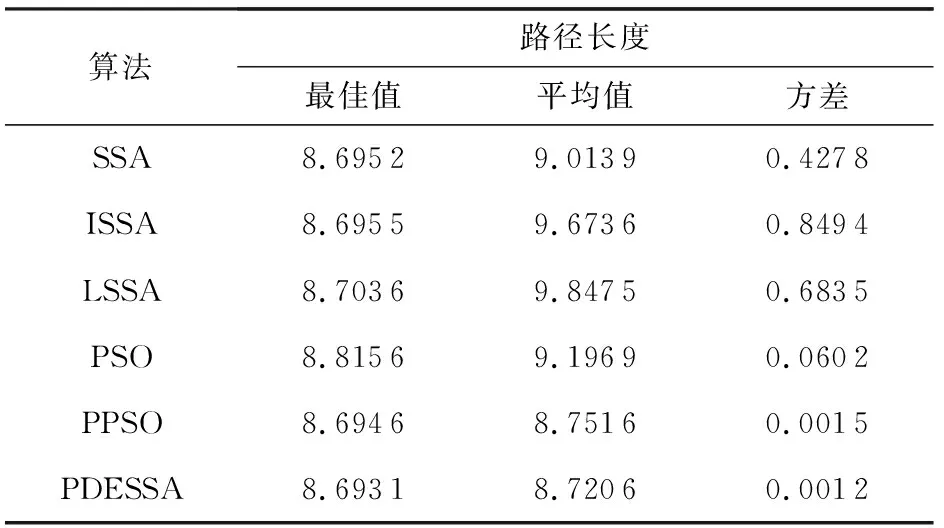
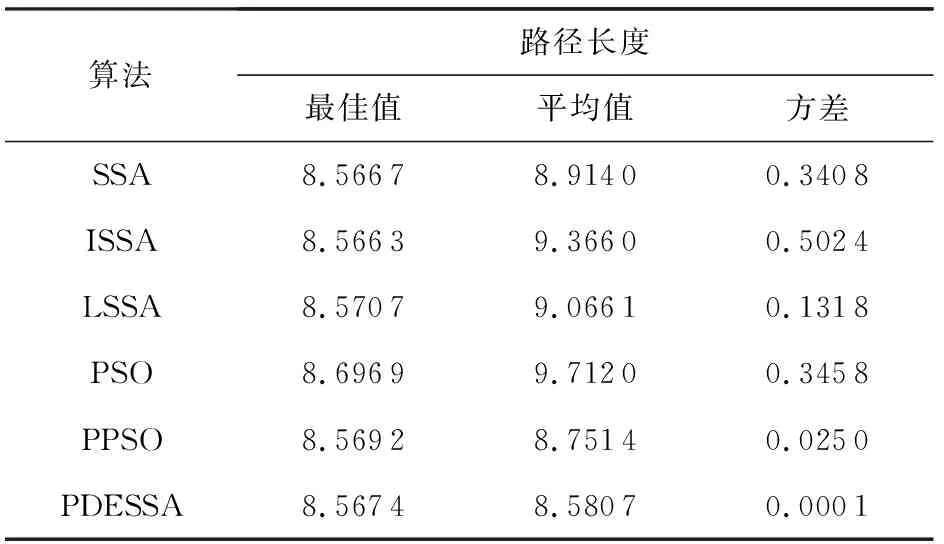
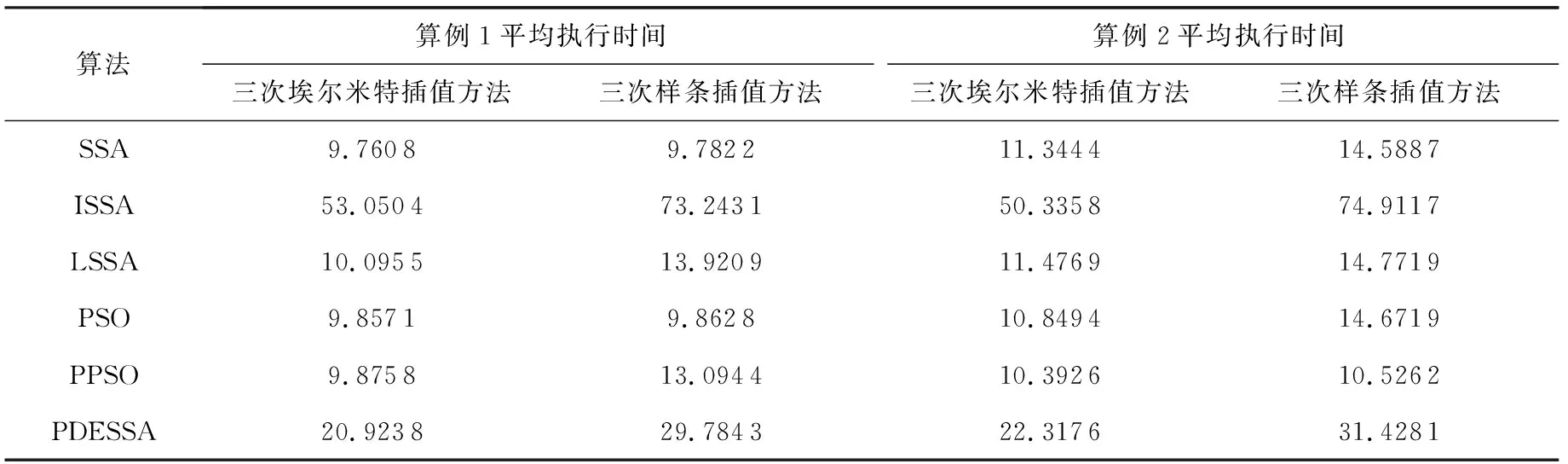
设在节点a≤x0

H(xi)=yi，

(10)

H′(xi)=mi(i=0,1,…,n)，

(11)

因插值节点一共有n+1个，当给出2n+2个条件时，便可唯一确定一个次数不超过2n+1的多项式H2n+1(x)=H(x)，其表达式的形式为

H2n+1(x)=a0+a1x+…+a2n+1x2n+1.

(12)

在由基函数构造埃尔米特插值多项式时，先求出插值基函数αi(x),βi(x)(i=0,1,…,n)，因而共得到2n+2个基函数，每个基函数为一个2n+1次多项式，并且满足:

(13)

(14)

βi(xk)=0，

(15)

(16)

由式(10)～(16)条件构造出的埃尔米特插值多项式为

(17)

作为分段式插值方法，埃尔米特插值在区间内生成一系列中间插值节点，从而构造出一条较光滑曲线.将埃尔米特插值方法融合到机器人全局路径的规划构建上，能够使机器人在移动过程中更加自然地避开障碍，形成更符合动力学原理特性的平滑路径.

三次埃尔米特插值问题的数学描述为：设y=f(x)是[a,b]上的实函数，x0,x1是[a,b]上相异的2点，且x0

(18)

H3(x)称为三次埃尔米特插值多项式，式(18)即为此问题的插值条件.

4.2 构建模型与适应度函数

4.2.1 求解问题的数学模型与算法编码方式

为了将智能算法更好地应用于移动机器人全局路径规划问题，充分发挥算法的优化作用，在建立该问题的数学模型时做3个假设：

1) 机器人的移动场景为2维有限空间；

2) 移动空间中任意分布着有限个静态障碍物，这些障碍物的位置可知且能以外切圆表示，无需考虑其高度；

3) 机器人被看作质点，其大小形状可以忽略.

基于算法处理的效率和统一性以及所规划出机器人路径的光滑性考虑，将各种不同形状的障碍物抽象为其各自的外切圆，以圆形表示.模型中正方形表示机器人的路径起点、终点，圆形区域为障碍区，其余为可移动区域.本文将基于这类环境和场景，进行移动机器人的全局路径规划，而这样的环境也能够与无人车间、智能仓库、特殊环境作业等许多实际应用场景相吻合.

在该问题模型的基础上，可使用本文算法PDESSA或其他群智能优化算法，求解出一条最优路径，而与三次埃尔米特插值方法相结合，各插值段的转折连接点即为路径节点.在本文的编码策略中，1条路径映射为算法中的1个个体，个体位置的每一维便依次对应于所映射路径的各节点坐标，即1个d维个体的1个维度值由1个路径节点的坐标数组(x,y)构成，而维数d则是路径上所有节点的个数.

设1条路径上共有m个节点，各节点的坐标为(xnode1,ynode1)，(xnode2,ynode2),…,(xnodem,ynodem)，路径的起点、终点坐标为(x0,y0),(xn+1,yn+1)，用三次埃尔米特方法对各节点间的连线进行插值，共产生n个插值点，坐标可表示为(xi,yi),i=1,2,…,n，那么由该路径的起点、包含m个路径节点在内的n个插值点、路径终点共n+2个有序点，即(xi,yi),i=0,1,…,n+1构成的连线就是机器人的移动路线.

4.2.2 构建目标函数

目标函数用于求解机器人全局路径问题的最优解，其适应度值便是评价求解结果和性能的量化值.评判所得到的1个路径是否最优，需要满足：

1) 不经过任何障碍物区域(没有碰撞)；

2) 产生的路径最短.

基于此2条件所构造的机器人路径规划问题适应度函数为

F=L(1+ρ×Z),

(19)

其中，惩罚系数ρ的值要足够大，以起到若发生碰撞便死刑惩罚的作用，本文取ρ=100，从而排除进化求解过程中那些穿越障碍物圆形区域的路径.L为从起点、每个插值点直到终点的序列点距离和，即路径长度，其计算为

(20)

其中，xi,yi和xi+1,yi+1分别是第i个和第i+1个插值点的横坐标与纵坐标.

Z用来判断插值点是否位于障碍物区域，即该路径是否经过障碍物，其初值为0，计算Z的代码段为：

fork=1:CN

Pk=max(1-Dk/CRk,0)；

Z=Z+mean(Pk)；

end for

其中，x，y分别是路径上全部插值点横、纵坐标的集合，CN是障碍数，CXk和CYk分别是障碍k的圆心横、纵坐标，CRk则是障碍k的圆形区域半径.Dk用于存储障碍k圆心到路径上各插值点的距离值.Pk为标志数组，用来判别每个插值点是否位于障碍k的圆形区域内，当路径中存在落入障碍区域的插值点时，说明路径未能避开障碍，此时Pk中对应于该插值点的标志值为正，有Z>0；否则数组Pk的所有元素都是0，有Z=0，这说明此路径没有经过任一障碍区域，所对应的目标函数适应度值为L.

4.3 机器人路径规划

为验证PDESSA算法对于机器人全局路径规划的有效性，将第3节的6种算法在相同环境下进行算例求解仿真实验，从而全面检验和分析PDESSA及5种对比算法分别与三次埃尔米特插值相结合，求解这一问题的寻优结果和性能.

为保障比较的公平性，6种算法均独立运行求解过程30次，种群规模N=50，最大迭代次数Max_iter=100.各算法的运行环境及参数设置也都与第3节相同，即参数值与各自算法的源文献和源代码保持一致.

4.3.1 基于三次埃尔米特插值方法的算法对比

1) 算例1：普通场景下6种对比算法的求解实验分析.

Fig. 11 Space scene diagram of case 1图11 算例1的空间场景图

算例1为普通障碍场景，机器人移动的起点和终点坐标分别是(0.0,0.0)和(6.0,6.0)，场景空间中障碍物的个数为6，将路径节点数设置为3，插值点个数设置为400.图11给出了机器人移动时的空间场景，表3则列出了此场景中各个障碍物的位置与大小.

Table 3 Location and Size of Obstacles in the Scene of Example 1表3 算例1中各障碍物的位置与大小

表4统计了对于普通障碍场景的算例1，6种算法30次求解得到的路径长度最佳值、平均值和方差.图12给出了本文算法PDESSA求解规划出的一条机器人移动路线.

Table 4 Solution Results of the Six Algorithms for Example 1表4 6种算法对算例1的求解结果

Fig. 12 Path planning curve of case 1 by PDESSA图12 算例1中PDESSA规划的路径曲线

2) 算例2：复杂场景下6种算法的求解实验分析.

算例2为较复杂障碍场景，机器人移动的起点和终点坐标分别是(0.0,0.0)和(6.0,6.0)，场景空间中障碍物的个数为10，将路径节点数设置为5，插值点个数设置为600.图13给出了机器人移动时的空间场景，表5则列出了此场景中各个障碍物的位置与大小.

Fig. 13 Space scene diagram of case 2图13 算例2的空间场景图

Table 5 Location and Size of Obstacles in the Scene of Example 2

表6统计了对于较复杂障碍场景的算例2，6种算法30次求解得到的路径长度最佳值、平均值和方差.图14给出了本文算法PDESSA求解规划出的一条机器人移动路线.

Table 6 Solution Results of the Six Algorithms for Example 2表6 6种算法对算例2的求解结果

Fig. 14 Path planning curve of case 2 by PDESSA图14 算例2中PDESSA规划的路径曲线

表4和表6分别统计了6种算法各自独立运行30次来求解2种不同复杂程度场景的算例1和算例2，规划出的路径长度的最佳值、平均值和方差.由表4和表6中的统计数据可以看出，无论对于普通亦或是较为复杂的障碍场景，PDESSA所求出的路径长度平均值和方差都是6种算法中最小的，这说明其求解效果和稳定性都更为出色.在最佳值方面，对于普通障碍场景，本文算法PDESSA的最佳值也是6种算法中最优的；对于较为复杂的障碍物环境，本文算法PDESSA的最佳值与SSA几乎相同，明显优于其他4种算法.由于PDESSA算法的最佳值始终名列前茅，而且平均值和方差更是优于其他5种对比算法，充分说明了其求解结果的有效性.同时，观察图12和图14也可看出，由PDESSA算法规划出的路径曲线平滑自然且能有效绕避空间中存在的各个障碍.实验结果和分析可知，在求解机器人路径规划问题上，相比于其他5种对比算法，PDESSA算法显现出明显的优越性，并具有更好的可靠性.

4.3.2 不同插值方法的对比和选择

1) 基于三次样条插值的算例求解对比实验

在求解移动机器人全局路径规划时，本文中采用了将PDESSA和其他群智能优化算法与三次埃尔米特插值方法相结合的方案，而与此同时，三次样条插值也是求解这一类问题时常被用到的方法.三次样条插值也是一种经典的分段式插值方法，能够通过一系列基于三次多项式的插值区间，构造出一条平滑流畅的曲线，该方法已被成功地应用到求解移动机器人全局路径规划问题中[36-37].下面在相同对比算法、参数设置、算例场景和实验条件下，将这6种算法分别与三次样条插值相结合，求解不同障碍场景下的机器人全局路径规划问题，如算例1和算例2，并与本文融合三次埃尔米特插值的求解方案进行对比分析，以便选择出一种更具优势和有效性的分段式插值方法，从而更好地与PDESSA等群智能优化算法相结合，高效、优越地求解移动机器人全局路径规划问题.

表7和表8分别统计了6种算法融合三次样条插值方法，各自独立运行30次，求解普通和较复杂障碍场景的算例1和算例2，得到的路径长度的最佳值、平均值和方差.

Table 7 Solution Results of the Six Algorithms Based on Cubic Spline Interpolation for Example 1表7 6种基于三次样条插值方法的算法对算例1的求解结果

Table 8 Solution Results of the Six Algorithms Based on Cubic Spline Interpolation for Example 2表8 6种基于三次样条插值方法的算法对算例2的求解结果

观察表7和表8中的统计数据可以很清楚地看出，对于2种不同复杂程度障碍场景的算例1和算例2，PDESSA算法与三次样条插值方法相结合所求得的路径长度的平均值和方差依然全部优于其他5种算法.在最佳值方面，对于算例1，本文算法PDESSA的最佳值也是6种算法中最优的；对于算例2，本文算法PDESSA的最佳值与ISSA，SSA算法基本相当，明显优于另外3种算法，而平均值和方差更是显著优于ISSA，SSA和其他对比算法，充分说明了其求解路径长度值的优越性和稳定性.

这些结果再次证明了本文算法PDESSA在求解移动机器人全局路径规划问题上，具有出色的稳定性和良好的适用性.

2) 基于2种不同插值方法得到的路径长度

将表4，6与表7，8中统计的路径长度数据进行比较可以看出，在求解普通障碍场景的算例1时，对于PSO算法，用三次埃尔米特插值方法所求出的路径长度最佳值、平均值和方差都优于用三次样条插值方法求出的值；对于ISSA和SSA算法，用三次埃尔米特插值方法求出的路径长度的平均值和方差都优于用三次样条插值方法；对于LSSA，其采用三次埃尔米特方法求出的路径长度最佳值和平均值更优；只有PPSO算法使用三次埃尔米特方法求出的值稍逊于三次样条插值方法；对于本文算法PDESSA，用三次埃尔米特插值方法求出的路径长度的最优值和方差都优于三次样条插值方法.这些结果表明用三次埃尔米特插值方法求出的路径长度并不是全都优于三次样条插值方法，但整体而言结果较优，而且每次运行求出的路径差异性较小，求解性能更稳定可靠.

对于较复杂的障碍场景，基于三次埃尔米特插值的求解方案优势更加显著，其中SSA，PSO，PPSO以及本文算法PDESSA使用三次埃米尔特方案求解算例2得到的路径长度的最佳解、平均值和方差，全都优于该算法采用三次样条插值的求解方案，使用三次埃尔米特插值的求解效果明显更为出色.

通过以上测试结果的比较和分析，可以清楚地看到对于不同复杂程度的障碍场景，融合三次埃尔米特插值的求解方案规划出的路径长度，跳跃性较小，稳定性更强，整体更为可靠，尤其是在较为复杂的障碍环境下，采用三次埃尔米特插值的方案求解效果更佳，优势更突显.

3) 采用2种不同插值方法的算法平均执行时间

表9统计了6种算法分别融合引入三次样条、三次埃尔米特2种不同的插值方法，各自独立运行30次求解算例1和算例2，得到的算法平均执行时间.

由表9可以看出，在求解算例1和算例2时，由于6种算法的寻优机制各异，这些算法的平均执行时间也各不相同.但当6种算法融合三次埃尔米特插值方法时，求解各算例所需的平均执行时间都小于该算法融合三次样条插值方法时求解同一算例的平均执行时间，显然前者的执行时间更短、效率更高.

由关于2种不同插值方式下路径长度和算法执行时间的实验结果与分析可知，采用融合三次埃尔米特插值的求解方案，求解移动机器人全局路径规划问题时，所规划出路径的长度整体更短也更加稳定，

Table 9 Average Execution Time of Algorithms with Different Interpolation Methods表9 采用不同插值方法的算法平均执行时间 s

并且执行算法所花费的平均时间也更少.因此，本文采用将三次埃尔米特插值方法与PDESSA算法相结合，求解移动机器人全局路径规划问题的方案是合理而且有效的.

5 结 论

为了更好地求解移动机器人全局路径规划问题，进一步拓展樽海鞘群算法的应用空间，本文针对樽海鞘群算法所存在的不足进行改进.首先在樽海鞘领导者位置更新公式中，引入上一代位和惯性权重，然后在整个算法的进化机制中引入具有不同进化机制的寄生-宿主双种群思想和生物学中的优胜劣汰思想，增强了算法的全局搜索能力，平衡了领导者广度搜索与深度挖掘之间的平衡，提高了对于局部极值的摆脱能力.而后通过对6种算法在10个不同特征测试函数上进行对比分析，仿真结果证明改进算法具有可靠的寻优能力.最后将改进算法与埃尔米特插值方法相结合，定义了编码方式，构造了以绕避障碍和最短路径为目标的适应度函数，求解机器人路径规划问题.通过6种算法在2种不同障碍环境下进行对比实验，验证了本文算法对于求解机器人路径规划问题的优越性.下一步将继续改进樽海鞘群算法的寻优能力和性能，进一步增强算法的稳定性和适应性，将其应用到更多复杂实际问题的优化求解中.

作者贡献声明：刘景森提出算法机制和应用方案，负责并参与论文的写作和修改；袁蒙蒙参与论文的撰写，提出算法和方案的实现代码，测试和分析实验数据；李煜参与论文的写作与修改，对研究方案进行理论分析.