一种联邦学习中的公平资源分配方案
田家会 吕锡香 邹仁朋 赵 斌 李一戈
(西安电子科技大学网络与信息安全学院 西安 710071)
随着物联网、大数据、5G网络架构的发展,机器学习(machine learning, ML)在自动驾驶、信息检索、能源检测等领域得到了广泛应用.机器学习通过训练模型对数据进行分析,提取有用的信息.随着手机等智能设备的快速发展,数据分布趋向于本地化.单个用户或机构通常拥有较小规模或较低质量的数据,仅使用这些数据进行训练容易导致模型过拟合,所以需要将参与方数据汇集到一起来训练模型.然而,出于数据的隐私考虑,各方通常不愿意将自己的数据直接共享给别人,从而形成数据孤岛问题.联邦学习(federated learning, FL)是面向这种数据孤岛现实场景而设计的机器学习范式.通过分享模型参数或梯度的方式,联邦学习参与方可在保持数据本地私有的情况下协作训练一个高性能的共同模型[1].
联邦学习自2016年由谷歌提出以后,就引起了学术界和信息产业界的巨大关注.这使得联邦学习场景下的许多方向也都得到了迅速发展,如安全和隐私保护.研究表明,仅上传部分参数或梯度,本地训练数据仍有可能会泄露给诚实但好奇的服务器[2].因此联邦学习通常与差分隐私[3]、同态加密[4]、安全多方计算[5]等技术结合来保护数据隐私[6].当联邦学习应用于银行借贷、预测警务、犯罪评估等重大决策场景时,公平性也引起了人们的重视.然而,传统的联邦学习并没有考虑公平性的问题,聚合模型可能会潜在地歧视一些特殊群体,特别是当训练数据本身就存在偏见时.一个典型的例子是在“替代性制裁的惩罚性罪犯管理分析”(correctional offender management profiling for alternative sanctions, COMPAS)算法中.美国法院使用该算法预测一个人再次犯罪的概率,从而对罪犯做出假释审核.研究发现,在同等条件下使用该软件,与白种人相比,非裔美国人会得到更高的犯罪评分[7].
造成联邦学习中这种不公平现象的原因之一是它的目标函数,联邦学习的目标函数是最小化各个参与者的局部损失和样本比例的加权平均,从而使模型可以拟合大多数设备的本地数据.在真实场景中,参与者之间的数据通常是高度异构的.且因为网络、设备、用户习惯等因素的影响,参与者拥有的数据量差距也比较大.因此简单使用上述方式可能得到较高的平均准确率,但不能保证单个参与者的性能.即最终聚合模型在参与者本地数据之间的准确率悬殊较大,这是不公平的,可能会影响聚合效果.因此设计一种优化算法来使联邦学习参与者之间性能分布更公平是非常重要的.
目前有许多文献致力于联邦学习公平研究,如文献[8]提出了一种名为AFL(agnostic federated learning)的联邦学习框架,在此框架下全局模型可以优化任何客户分布混合而成的目标函数但是它们仅优化单个最差客户的性能,适用于小规模客户且缺乏灵活性.文献[9]中作者提出了一种新的目标函数q-FFL(q-Fair Federated Learning)来使参与者准确率分布更均匀,但该方法无法提前确定最佳的参数q值来达到公平性和有效性的平衡,且算法在本地数据异构较强时较难收敛.
在本文中我们提出了α-FedAvg算法,引入Jain’s Index和α-fairness来研究联邦学习模型公平性和有效性的平衡.该算法可以在保持联邦学习模型整体性能不损失的情况下,有效减小各参与方准确率分布的方差,使准确率分布更均衡.与文献[9]相比,我们的方法更简单,并且可通过算法在训练之前确定参数α的取值,而不需要该文中所述使用多个参数值训练获得全局模型后,验证模型性能再从中选择表现较好的参数值.
在本文的设定中,参与者是诚实的,它会如实地执行协议并向服务器上传最新的梯度和准确率.以合作的方式,获得比单独训练较好的本地模型.服务器是诚实但好奇的,它在诚实执行协议的同时可能会从参与者上传的参数中推测出一些敏感信息.因此我们的算法中也有相应的隐私保护机制.我们的应用场景为一些金融或医疗机构.在这些机构中,协同训练中谎报参数可能会付出沉重的法律代价.对于法律约束较弱的一般场景,参与者可能是自私的,会通过谎报模型在本地数据上的准确率来影响聚合过程的情况,我们在3.4节扩展部分也给出了解决方案.
本文的主要贡献包括4个方面:
1) 将Jain’s Index引入联邦学习领域来度量公平,并同时给出了系统有效性的度量.
2) 通过研究α-fairness中参数α对联邦学习模型公平性和有效性的影响,我们采用一种基于梯度的算法来确定最佳α值达到二者之间的权衡.
3) 提出了α-FedAvg算法,在保证原有模型性能的基础上有效提高公平性,且该算法具有可扩展性,可与已有的隐私保护技术相结合.
4) 我们在2个标准数据集MNIST和CIFAR-10上评估了α-FedAvg算法.并分别在图像、表格、文本类的数据集上与最新的其他3种公平方案进行了对比.实验结果表明,本文提出的算法实现了联邦学习模型公平性和有效性的平衡,且效果优于其他方案.
1 相关工作
近几年,机器学习算法的公平性得到了人们的高度重视,公平方向的研究不断涌现.总的来说,一个公平的算法不会基于其需要的特征歧视或者偏向于某些特定群体.通常机器学习算法消除歧视追求公平的方法可分为3类[10]:
1) 预处理(pre-processing).预处理考虑到算法不公平的原因可能是训练数据的问题,即受保护变量的分布是有歧视/不平衡的,因此预处理通常会改变受保护变量的样本分布来消除歧视.如文献[11]中作者提出了一种歧视意识(discrimination-aware)的审计过程,它与常规训练分类器的过程类似,主要是增加了歧视测试模型.文献[12]中作者借用了生成对抗网络(GAN)的思想,提出了FairGAN,它可以从在保证数据可用性的基础上从原始数据中生成更公平的数据用于训练,从而产生公平的模型.
2) 中处理(in-processing).中处理考虑到算法本身可能会产生偏见,因此中处理通常会尝试修改算法或增加一些公平约束,从而消除模型训练过程的歧视.如文献[13]中作者针对回归问题损失函数引入了公平正则器(fairness regularizers),且通过改变正则化权重来权衡给定数据集的准确性和公平性.文献[14]中作者通过增加约束来从训练集中学习到一个非歧视预测器.
3) 后处理(post-processing).后处理中将算法和模型视为黑盒,它倾向于对模型输出进行一定变换来提高预测的公平性.如文献[15]中作者介绍了一个开源的Python工具包AIF360(AI Fairness 360),为公平研究者提供一套共享和评估算法的通用框架,它包括一套完整的数据和模型公平度量标准以及缓解歧视的办法,研究人员可根据需求选择最适合的工具应用.
先前的机器学习公平研究大都聚焦于中心化设置而没有考虑分布式情况.联邦学习作为一种有前景的分布式机器学习范式,近几年也吸引了大量公平研究者的目光.由于应用场景不同,对公平的需求也不一样.总的来说,以联邦学习为主的分布式机器学习公平性研究也可分为2个方向:
1) 引入激励机制,参与者根据自己在聚合中的贡献得到不同的奖励(如金钱激励或得到不同的最终模型).如文献[16-17]中作者都设计了一种本地信誉互评机制,这种机制会评估参与者在学习过程中的贡献并迭代更新信誉值,使得参与者最终获得与其贡献相匹配的聚合模型.不同的是文献[17]中作者使用区块链进行交易,改变了传统联邦学习的B/S模式,且设计了一种3层洋葱式加密方案来保护参与者隐私.文献[18]中作者提出了一种分层联邦学习框架,首先基于参与者本地数据量的多少将其分为几个不同的贡献水平,在此框架下进行训练,不同水平的用户将收到不同的模型更新.
2) 参与者获得有效模型的机会均等.减小参与方之间或参与者内部训练和测试数据准确率分布的方差[8-9,19-21].本文的工作也属于这一方向.在文献[20]中作者证明了经验风险损失最小随着时间的推移会扩大群体之间的差异,因此作者开发了一种基于分布式鲁棒性的优化方法.与文献[7]相似,这种方法通过优化少数最坏群体的风险损失来达到公平.文献[19]中作者提出了AgnosticFair框架,解决当测试数据与训练数据分布不同时,在未知测试数据上达到公平的问题.文献[21]中作者提出了一种算法FedFa,它基于双动量梯度,可以加快模型收敛,并且采用了一种基于参与者训练数据准确率和训练频率的权重选择算法来达到公平.
2 理论基础
在本节中,我们主要介绍本文用到的相关理论,包括联邦学习和公平度量(fairness measure).
2.1 联邦学习
联邦学习是一种分布式机器学习框架,旨在保护数据隐私.联邦学习中通常有2种实体:参与者(数据拥有者)和服务器(模型聚合者).参与者有多个,记为{P1,P2,…,PN}.他们拥有各自的数据集{D1,D2,…,DN}.在联邦学习框架下,参与者之间不需要交换原始私有数据集,通过本地训练更新模型参数,并上传参数至中央服务器聚合的方式协同训练模型.
在联邦学习框架中,令K表示每轮聚合时的参与者个数,Dk表示第k个参与者拥有的数据集,其元素个数为|Dk|=nk,n表示所有参与者的样本总数,则联邦学习的目标是优化全局损失函数[1]:
(1)
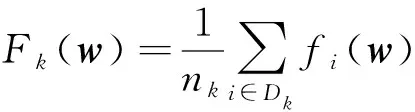
2.2 公平度量
在资源分配中,决策者进行资源分配时,不仅要考虑资源分配的有效性,还需考虑它的公平性.公平度量是资源分配中量化当前分配方式公平程度的方法,它通过一个函数f(x)将向量x∈映射为一个实数,且需满足5个性质[22]:
1) 连续性.公平度量f(x)是关于变量x∈的连续函数.
2) 单调性.当有2个用户时,公平性f(θ,1-θ)随着2元素之间差异|1-2θ|的增加而减小.
3) 同质性(homogeneity).公平度量f(x)的值与x代表的数学含义无关,只需统一即可.f(x)是一个齐次函数,满足f(x)=f(x)×t0=f(x×t),∀t>0,且对于任何单个用户都有|f(x)|=1.

5) 划分无关(irrelevance of partition).f(x)的值与x的划分无关,如果对x进行划分,可通过一定公式递归计算得到最终结果.
受到公平资源分配的启示,在本文中我们将联邦学习中的全局模型作为一种资源,其在各个参与者本地数据集上的准确率分布组成向量,使用Jain’s Index和α-fairness公平度量,保证联邦学习的公平性和有效性.Jain’s Index的定义为
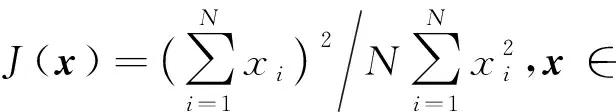
(2)
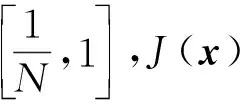
α-fairness通过改变参数α的取值来达到系统公平和效率之间的权衡,α值越高代表分配越公平,但同时系统有效性可能随之减小.在此框架下单个用户效用定义为
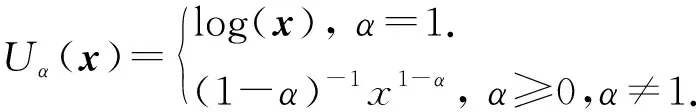
(3)
3 方案设计
在本节,我们首先会给出联邦学习过程中公平性和有效性的度量方法;然后提出一种算法确定最佳的α值,达到二者之间的权衡;最后我们利用求出的α值对联邦学习聚合过程重新加权,提出了一种α-FedAvg算法来产生更加公平的全局模型,并在扩展部分给出了应对自私参与者的解决方案.
3.1 联邦学习公平性和有效性的度量方法
参考2.1节所述的联邦学习的训练过程,我们用K表示每轮聚合时的参与者个数,pk表示参与者k本地训练的模型在中央服务器聚合时所占的权重,集合{a1,a2,…,aK}表示聚合后的全局模型wg用于各参与者本地数据上的准确率,用Rk=akpk表示聚合后参与者k获得的实际效用(utility),则本次训练过程中系统有效性(effificiency)量化为
(4)
系统公平性量化为
(5)
E和J都是0~1之间的实数,E值越大代表聚合模型越有效,加权平均准确率越高.J值越大表示聚合模型越公平,参与者之间准确率分布越均匀.
3.2 联邦学习公平性和有效性的权衡
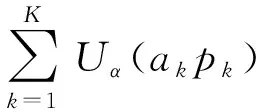
(6)
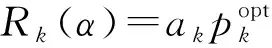
(7)
为了研究函数J(α)和E(α)的单调性,我们在α的定义域内分别对这2个式子求导,判断导数的正负.当α>1时,得到了2条定理,详细证明过程参考附录部分.
定理1.联邦学习系统公平性J(α)随α的增大而增大.
定理2.联邦学习系统有效性E(α)随α的增大而减小.
类似的工作在资源分配领域已经取得了巨大的进展,如文献[23-24].通过定理1、定理2可知,α取值会影响联邦学习系统有效性和公平性,因此我们需确定最佳的α取值来达到二者之间的平衡.我们的目标是在确保达到经典联邦学习最终模型同等有效性ET(阈值)的基础上,最大化系统公平性,即可以被描述为优化问题:
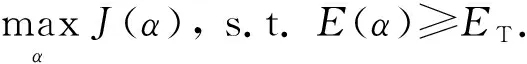
(8)
由定理1,2可知,当E(α)=ET时,α的取值为最优解.因为等式E(α)=ET中α在指数位置直接求解较为困难,利用该函数的单调性,我们使用一种更为简单有效的基于梯度的方法求解,通过逼近阈值ET来确定最佳α的取值.该方法可总结为算法1,其中{a1,a2,…,aK}为准确率,ET为有效性阈值;参数λ表示容忍误差,Λ表示改变步长大小,τ表示迭代过程中当α取负数时代替它的最小正实数,i表示迭代次数.
算法1.基于梯度的逼近算法.
输入:{a1,a2,…,aK},ET;
输出:α.
① 初始化λ=10-5,Λ=1,τ=10-10,α0=1,i=0;
② repeat
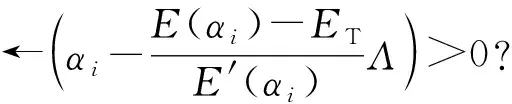
④ if (E(αi+1)-ET)(E(αi)-ET)<0 then
⑤Λ←Λ/2;
⑥ end if
⑦i←i+1;
⑧ until (|E(αi)-ET|<λ).
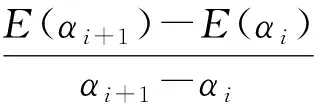
3.3 公平联邦学习算法(α-FedAvg)

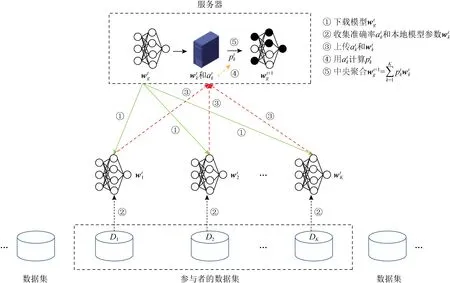
Fig. 1 Fair federated learning framework图1 公平联邦学习框架
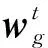
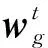
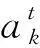

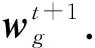
算法2.α-FedAvg.
输入:参与者个数K,聚合次数T,本地批大小B,本地时期数E,学习率η,参数α;
输出:全局模型wg.
服务器执行:

② for轮数t从0~T-1
③SK←选择K个参与者;
④ for参与者k∈SK,并行执行
⑤ ift≠0
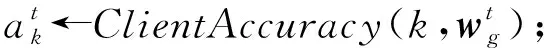
⑦ end if
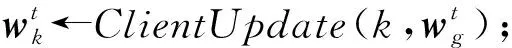
⑨ end for
⑩ for参与者k从1~K
参与者k执行:
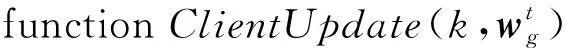
②Bk←将数据集Dk划分为小批量;
③ for时期e从1~E
④ for批量b∈Bk
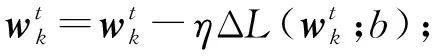
⑥ end for
⑦ end for

⑨ end function
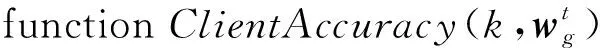
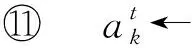
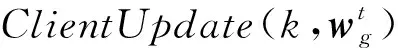
3.4 算法扩展
α-FedAvg算法设定每轮中所有参与者都会诚实地向服务器汇报本地模型参数和准确率,这使得它的应用场景具有很大的局限性.对于一般场景中可能存在的会谎报准确率的参与者,我们也给出了解决方案:通过参与者提交部分合成数据、服务器进行验证的方式,保证参与者汇报准确率的真实性.同时服务器可通过设定容忍参数将超出阈值的参与者踢出聚合过程.
合成数据发布技术是通过发布合成的数据集,来取代对原始数据集的查询结果,且生成的合成数据可以隐藏原始数据中的敏感信息.目前,该领域的发展已经非常成熟.我们可使用文献[26]中提出的基于贝叶斯网络的差分隐私合成数据发布方法.在预处理阶段,每个参与者都先与服务器约定好密钥,使用该方法,以本地测试数据为原型生成合成数据集并将加密后的数据发送给服务器.服务器端收到后解密并存储数据.服务器端设定2个参数:容忍误差λg和容忍次数阈值Tg.服务器可在每轮中选取部分参与者,验证全局模型在该参与者的合成数据集上的准确率与参与者提交的准确率是否一致,误差超过λg则容忍次数加1,容忍次数超出阈值Tg则将会被服务器标记为不可信,无法参与后续的聚合过程.该方法有效地保证了参与者提交准确率的真实性,保障了存在自私参与者中的α-FedAvg算法的公平性.
3.5 通信和计算开销
表1展示了每一轮迭代中2种算法的计算和通信开销对比,其中K代表参与者个数,n代表模型参数个数,t1代表前向传播计算时间,t2代表反向传播时间,E代表本地训练轮数.
1) 通信开销.对于传统的FedAvg算法,服务器需要与K个参与者通信,因此其通信开销为O(K).每个参与者仅需与服务器通信,因此其通信开销为O(1),本文所提的α-FedAvg算法也是如此.
2) 计算开销.传统的FedAvg算法中,服务器基于参与者上传的K个模型计算全局模型,每个模型包含n个参数,对于每个参数计算其平均值,因此时间复杂度为O(Kn).我们提出的α-FedAvg算法在此基础上,通过K个准确率计算对应的模型权重,其时间复杂度为O(2K),因此总的时间复杂度为O(2K+Kn).传统的FedAvg算法中,参与者基于本地数据优化模型,本地训练轮数为E,每一轮中,通过神经网络优化算法更新模型参数,包括一次前向传播和反向传播,因此其时间复杂度为O(E(t1+t2)).我们所提的α-FedAvg算法在此基础上,需要根据全局模型计算准确率,其相当于一次前向传播过程,时间复杂度为O(t1),因此总的时间复杂度为O(E((t1+t2)+t1).
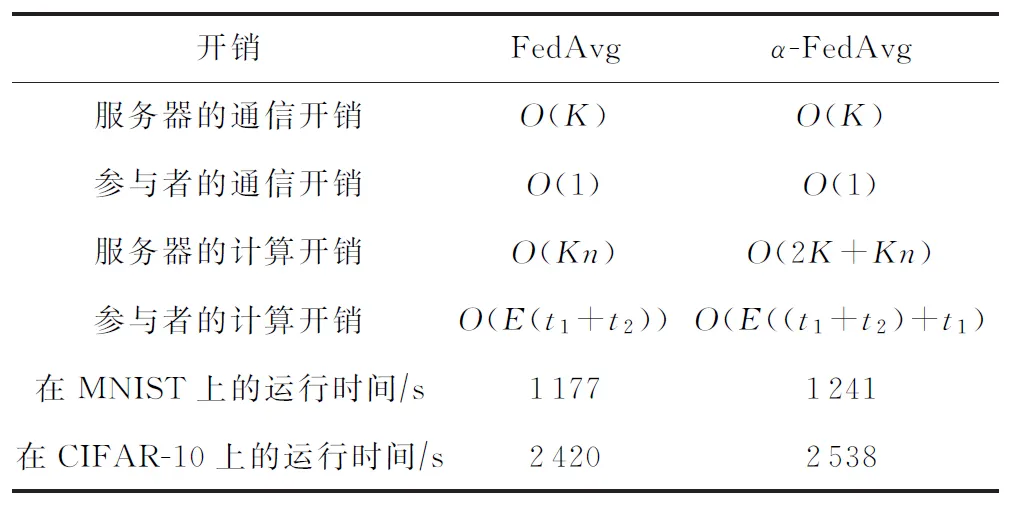
Table 1 Communication Cost and Computation Cost表1 通信开销和计算开销
我们在实验过程中记录了相同条件下多次运行100轮经典联邦学习FedAvg和本文算法所需要的平均运行时间,它们的差值约在2 min以内.总的来说,我们所提的算法在保证联邦学习公平性和有效性的基上,复杂度与原来相差不大,不会引入过多的计算开销和通信开销.
4 实验结果
在本节中,我们评估了本文所提算法α-FedAvg的性能.首先我们描述了实验设置,包括数据集和本地模型;然后展示了α-FedAvg相比于经典联邦学习算法FedAvg的有效性;最后将α-FedAvg和已有的其他公平联邦学习算法作了对比.
4.1 实验配置
1) 数据集.我们在深度学习常用的2个基准数据集上实现了我们的算法,第1个是手写数字识别数据集MNIST,它包含了60 000个训练样本和10 000个测试样本,每张图片为数字0~9中的1个,且数字位于图片中央.为了提高算法的泛化能力,我们在训练之前对原始数据做了一些增强处理,如将每张图片旋转任意角度或进行平移变换.为了更好地模拟真实世界,将数据集在参与者间进行划分时采用non-IID不平衡划分方式.首先我们将数据集按照数字标签排序,然后将其划分为1 200个分片,每个分片包含50张数据,设定每个参与者拥有的最大分片数为30,最小分片数为1.实验中共100个参与者,每个参与者拥有一定分片的数据,且所有参与者分片总数一定.这种划分方式保证了每个参与者最多拥有3个类别的数字样本,且相互之间样本数量差距悬殊.第2个是CIFAR-10数据集,它包含50 000个训练样本和10 000个测试样本,共10个类别,每个类别有6 000个图像,每张样本是由32×32个像素点组成的彩色图像,这个数据集最大的特点在于将识别迁移到了普适物体,数据中需要提取的特征较大且含有大量噪声,识别物体的比例也不一样,因此CIFAR-10数据集对于图像识别任务更具有挑战性.CIFAR-10数据集在参与者间的划分方式也采用non-IID不平衡设定,实现细节和MNIST类似.
2) 模型.如图2所示,我们在实验中用到了2种模型:①一个最简单的多层感知器(MLP),包含一个隐藏层;②一个经历2次卷积和最大池化的卷积神经网络(CNN).2种模型中激活函数都使用ReLU并加入Dropout层缓解过拟合的发生.

Fig. 2 Neural network architectures图2 神经网络结构
3) 实现.我们在深度学习框架Pytorch上实现了我们的代码,用电脑模拟了联邦学习的训练过程,虚拟对象包括一台服务器和100个参与者.
4.2 实验和结果
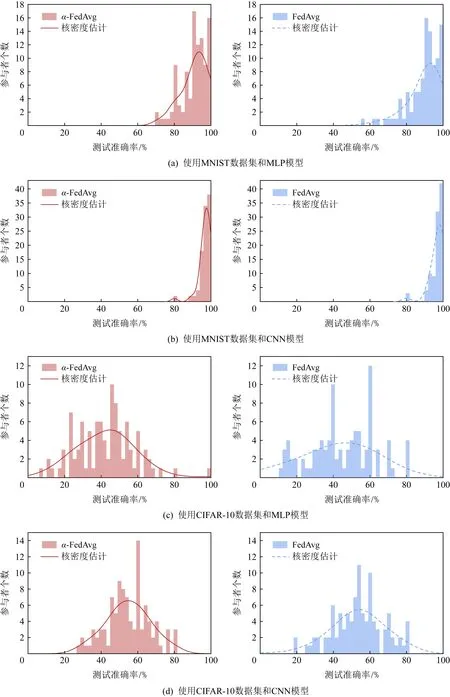
Fig. 3 Changes of the number of participants under different test accuracy intervals in two algorithms图3 2种算法中参与者个数在不同测试准确率区间的变化
为了突出本文所提算法α-FedAvg的公平和有效性,我们将其与经典联邦学习算法FedAvg做了比对.为了排除无关因素的影响,我们控制2种算法的实现条件基本相同,包括参与者之间的数据划分、全局模型初始化数值和一些参数设置.实验中,我们设置每轮聚合中参与者个数K=10,本地批大小B=5,本地时期E=5,学习率n=0.01.我们用MNIST和CIFAR-10数据集及其模型组合共进行了4组实验,分别测试最终模型在各个参与者本地数据集上的准确率,得到1组数值.我们将整个准确率区间0~1共分为50份,统计这组数值落入对应区间的客户数目,画出频数分布直方图.图3展示了α-FedAvg和FedAvg算法经过100轮聚合后,最终模型在各个参与者的准确率分布图,曲线部分为准确率数组的核密度估计,通过核密度估计图可以比较直观地看出数据样本本身的分布特征.以图3(a)为例,通过左右2部分子图对比,我们可以看出α-FedAvg算法中参与者准确率分布更集中,曲线更陡峭,从而反映出参与者之间准确率方差更小,系统更公平.
表2进一步描述了2种算法得到的参与者准确率的统计分布和系统度量对比,其中T表示中央聚合次数,E表示有效度量,J表示公平度量.我们选取了T=5和T=100的情况研究聚合次数是否对算法表现造成影响.从表2中可以看出,无论是T=5或T=100,本文所提的α-FedAvg算法都可以提升聚合模型的公平和有效性,且在保持参与者的平均准确率不变或略有增加的情况下,提升最坏参与者的准确率,降低最好参与者的准确率,减小参与者之间准确率分布的方差,即α-FedAvg算法可在达到公平需求的同时保持总体性能不受影响.
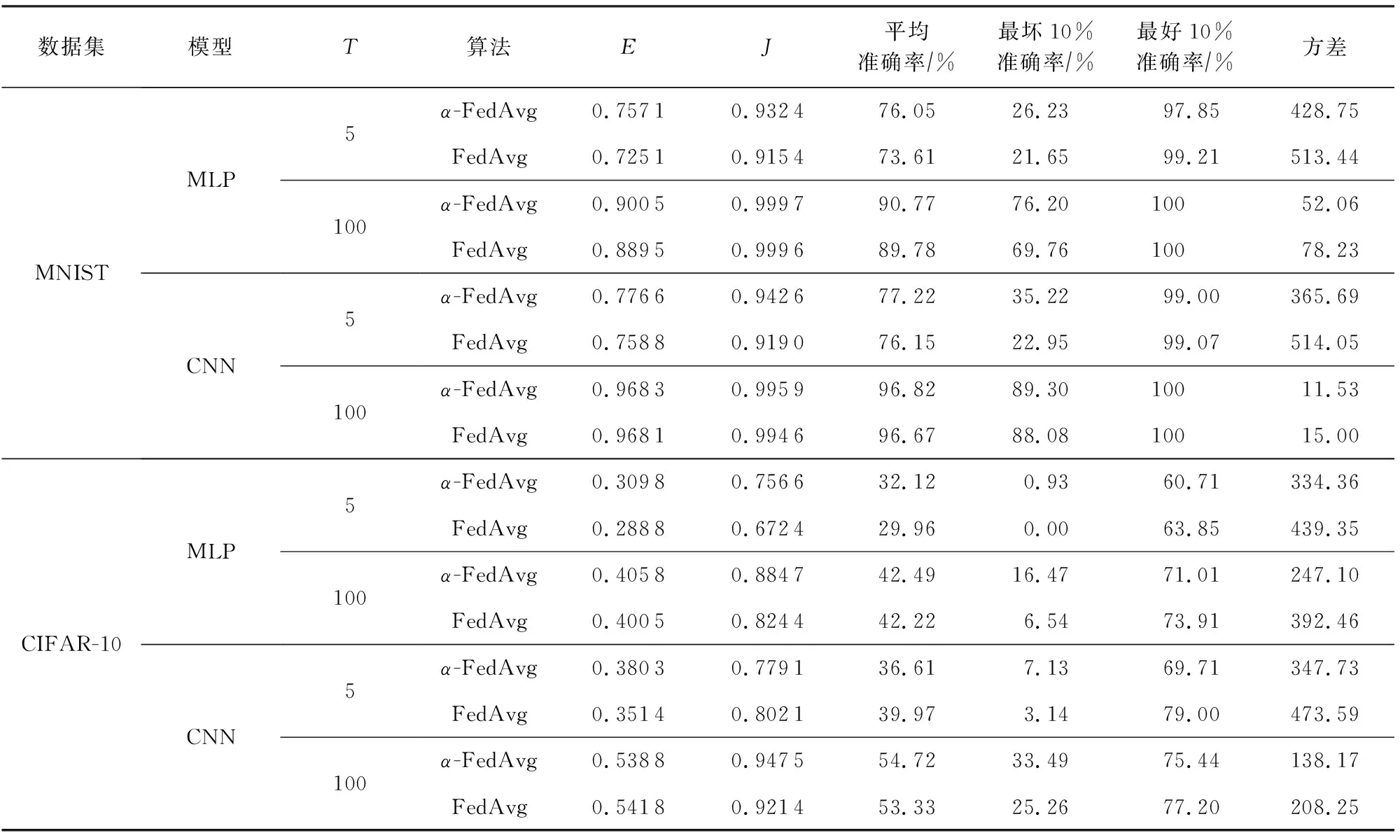
Table 2 Statistics of the Test Accuracy Distribution for Our Algorithm Compared with Normal Federated Learning Algorithm FedAvg表2 本文算法与常规联邦学习算法FedAvg相比在测试集上的准确率分布
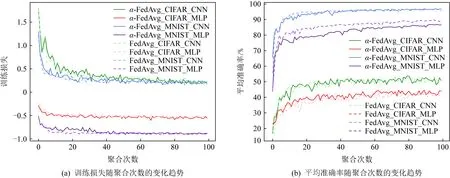
Fig. 4 Training loss and average accuracy changing with the communication rounds图4 训练损失和平均准确率随聚合次数的变化
α-FedAvg算法取得的公平性已在图3和表2得到了论证.接下来我们会进一步研究它的有效性.在训练中,我们记录每一轮聚合后的模型在参与者本地训练数据上的平均准确率和损失函数值,画出图4所示曲线.从图4(a)中可以看出,本文提出的α-FedAvg算法与经典联邦学习算法FedAvg的收敛速度基本一致;从图4(b)中可以看出,2种算法在训练集上的平均准确率变化情况也大致相同.图4再一次说明我们的算法是有效的,在追求公平需求的同时不会影响联邦学习的整体性能.
4.3 其他对比实验
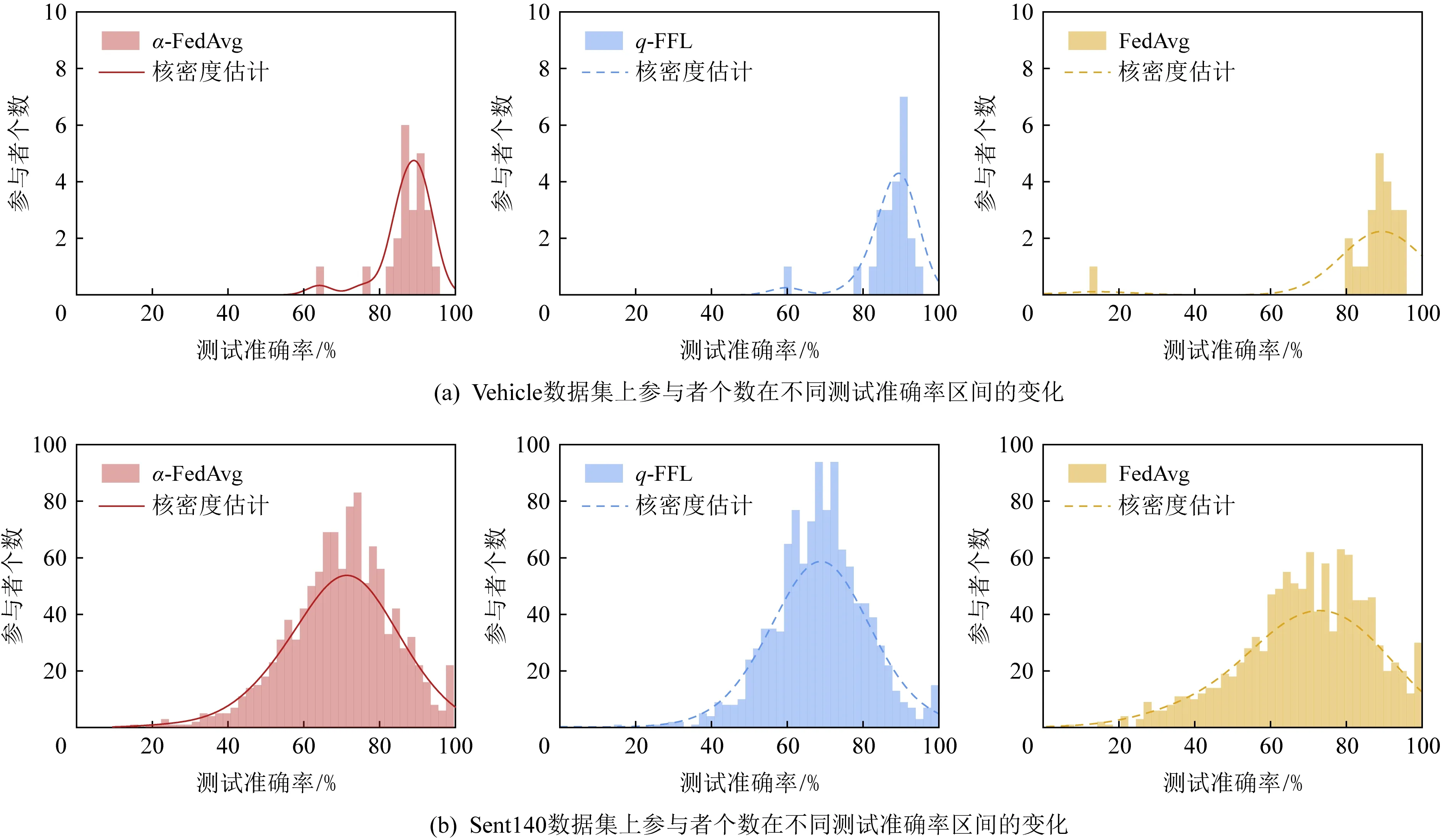
Fig. 5 Changes of the number of participants under different test accuracy intervals in three algorithms图5 3种算法中参与者个数在不同测试准确率区间的变化
在本节中,我们将α-FedAvg与已发表的其他在联邦学习中施加公平约束的方案作了对比,与我们工作相似的最新成果是2020年发表的文献[9,21].在文献[9]中,该文作者提出了一种新的更公平的联邦学习优化目标q-FFL,为了解决这一优化目标,设计了一种高效的学习算法q-FedAvg,它能有效降低学习到的最终模型在设备间准确率分布的方差,同时保证平均准确率不受影响.文献[21]中作者提出了算法FedFa,它通过参与者的频率和准确率来调整聚合权重,使最终模型对参与者来说更公平.我们分别复现它们在Vehicle,Sent140,Synthetic,Femnist[27]数据集上的实验结果,并在此基础上实现了我们的算法和基准算法FedAvg.其中Vehicle为图像数据集,由23个传感器中收集的声学、地震和红外传感器数据组成.我们将每个传感器作为一个参与者,模型使用SVM完成基本的二分类问题.Sent140数据集是用于情感分析任务的文本数据集,模型使用2层长短期记忆网络(LSTM)和一个密集连接层.Synthetic是一个采用文献[28]中设定的合成数据集,使用简单的回归模型来做分类任务.Femnist是一个衣物图像数据集,模型使用MLP.图5展示了α-FedAvg与其他2种算法在相同条件下训练得到的最终模型在参与者本地数据集上准确率的分布情况.可以看出相比于FedAvg,α-FedAvg的曲线更陡峭,直方图更集中,方差更小;q-FFL与α-FedAvg结果较为接近.
我们在表3中进一步报告了最终准确率的统计分布,包括平均准确率、最坏10%准确率、最好10%准确率和方差.可以看出,在其他3个数据集上,α-FedAvg算法在保证平均准确率与基准算法FedAvg相似甚至略好的情况下,参与者之间的准确率方差都比其他2种公平算法更小一点.而q-FFL虽然在Sent140上方差小于α-FedAvg,但相较于基准算法,损失了准确率.而α-FedAvg算法既保证了有效性又保证了公平性.

Table 3 Statistics of the Test Accuracy Distribution for Our Algorithm Compared with q-FFL and FedFa表3 本文算法与q-FFL, FedAvg和FedFa相比在测试集上的准确率分布统计
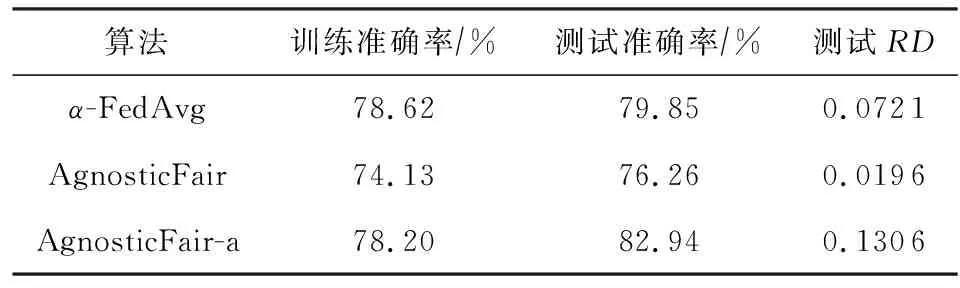
Table 4 Model Performance Under Data Distribution Shift表4 在数据分布转移下的模型性能
从表4中可以看出,我们的算法测试准确率和公平性都介于不加公平约束的AgnosticFair-a和AgnosticFair算法之间.这说明算法α-FedAvg在测试集存在分布转移时也是有一定公平作用的,因为我们在每轮中收集了测试集上的准确率来调整权重.AgnosticFair算法在该场景下能达到较好的公平性,但是可能会以牺牲准确率为代价.
5 总结和未来展望
在本文中,我们提出了一种新的联邦学习算法α-FedAvg,使聚合模型在参与者本地数据上的准确率分布更均衡.首先,类比资源分配领域,我们给出了联邦学习系统公平和有效性的度量方法;然后我们引入了α-fairness并研究了参数α对公平和有效性的影响,通过一种算法确定了我们需要的α值;最后根据求得的α值和权重pk计算公式对聚合过程重新加权,提出了α-FedAvg算法.α-FedAvg可在保持与经典联邦学习算法FedAvg同等有效性的基础上,使参与者之间准确率方差更小,即聚合结果更公平,实验结果证明了我们提出的方法是有效的.进一步的工作也非常具有吸引力.特别是,研究如何抵御上传伪造模型参数来影响聚合模型公平的恶意攻击者,并设计适用于本文算法的激励机制,鼓励更多的参与者加入我们的聚合过程.
作者贡献声明:田家会提出研究思路,设计研究方案,负责实验设计和撰写论文;赵斌提出研究思路,设计研究方案;吕锡香、邹仁朋和李一戈参与论文修订.

