基于E-DP和DLP一种无限非交换群上的密钥交换协议

东莞职业技术学院现代工业创新实践中心 张静

首先，本文提出与分解问题等价的一个困难问题：等价分解问题。其次，基于等价分解问题(E-DP)和离散对数问题(DLP)，提出了一种无限非交换群上的密钥交换协议。在协议中，通过半直积的运算法则，使共享密钥同时包含两个困难问题。这两个困难问题共同保证了密钥交换协议的抗攻击性。最后利用代数攻击和暴力攻击进行分析，证明了协议具有较高的安全性。

Sidelnikov等人提出在无限非交换群和半群上建立公钥密码系统的思想[1]。非交换群上的公钥密码系统主要是应用困难问题隐藏因子，公开的困难问题有共轭搜索问题、分解问题、子群元素搜索问题、离散对数问题、同态搜索问题等。许多研究已经提出了一些非交换代数结构上基于困难问题的密钥交换协议。在文献[2]中，作者提出了无限非交换群上基于分解问题的密钥交换协议[2]。

在文献[3]中，作者提出了辫群上基于共轭搜索问题的一种新的密码系统[3]，其中辫群是一种无限非交换群，并具有很好的密码特征。随着量子算法和分解算法的发展[4]，只应用一个困难问题已经不能保证密码系统的安全性。而且单独应用共轭搜索问题构建的密码系统也已经被证明对于安全性是不充分的[5]。为了提高安全性需要同时使用几个困难问题，2007年，Eligijus等人同时使用共轭搜索问题和离散对数问题在非交换群上构建了一种密码协议，并阐明了同时使用两个困难问题足够保证密码交换协议的安全性[6]。2013年，Maggie Habeeb等人第一次将群的半直积用到密码系统中，并提出了一种基于半直积运算的密码交换协议[7]。

本文，首先提出了等价分解问题，它是分解问题的一种变形，它的求解困难性与分解问题的困难性相同。其次通过半直积的运算法则，构建了基于离散对数问题和等价分解问题在无限非交换群上的密钥交换协议。因为目前在非交换群上没有分解困难问题的有效量子算法，并且同时在密钥协议中设置两个困难问题可大大提高密钥的安全性，所以该密码交换协议具有抗量子攻击性。最后，通过代数攻击和暴力攻击分析，阐明了该协议的安全性。

1 数学知识

定义1 (半直积)：(G,·)和(G',。） 是两个半群， Aut(G)是G的自同构群，其二元运算是合成运算。ρ:G'→Aut(G)是一个自同构，G和G'的半直积是一个元素对集合：

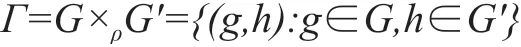
其二元运算定义为：

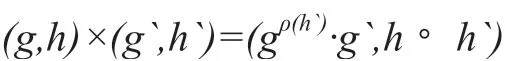
其中，g,g`∈G和h,h`∈G`,gρ(h`)表示g在自同构ρ(h`)下的像。

如果G`=Aut(G)，ρ=idG,那么

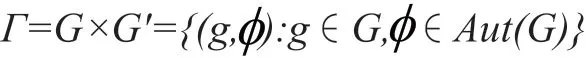
其二元运算为：

Bij(G)表示G→G上所有双射构成的集合。在本文的密钥交换协议中，只需要映射是双射，即在集合中，仍按以上方式定义二元运算其中表示双射的合成运算，并定义1(g,φ)， m∈Z+。如果G是一个群，对于∀a,b∈G，让，显然 是一个双射，并且那么有

定义2 (中心化子)：G是一个群，g∈G，那么集合

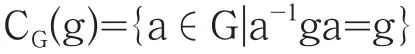
是g的中心化子。

事实上，CG(g)是G的子群，对于∀a∈CG(g)满足ag=ga。

定义3 (等价分解问题): G是一个群，对于∀μ,找到满足μ=α.ϑn，其中n∈Z+。

定义4 (离散对数问题): G是一个群，对于∀μ,找到满足

2 密钥交换协议

公钥：g

私钥：m,n,k,h

步骤1：Alice选择私钥m∈Z+和k∈G满足kg≠gk，那么她有映射计算中心化子CG(k-1)，选择中心化子的一个子群G'，使得|G'|≥N，其中N是正整数。Alice计算积：

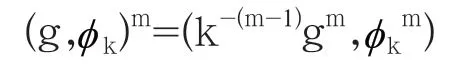
让A=k-(m-1)gm，A'=k-1A=k-mgm, 发送A'和G'给Bob。

步骤2：Bob选择私钥n∈Z+和h∈G'满足hg≠gh，那么他有映射Bob计算积：

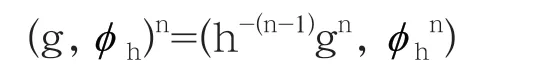
让B=h-(n-1)gn,B'=h-1B=h-ngn,发送B'给Alice。

步骤3：Alice计算：

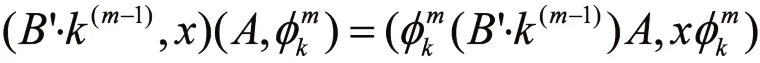
如果你在威尼斯，不如徜徉在迷人的广场下或者乘坐浪漫的贡多拉（威尼斯特有的小船），当然，起泡酒必不可少，与两三好友享受此地的浪漫。如果贡多拉的浪漫不适合你，那就试找家地道的意大利餐厅，坐下吃吃意大利面吧，开瓶当地红酒相配，相信那会是番茄肉酱意粉的最佳拍档！

这样Alice的密钥为：

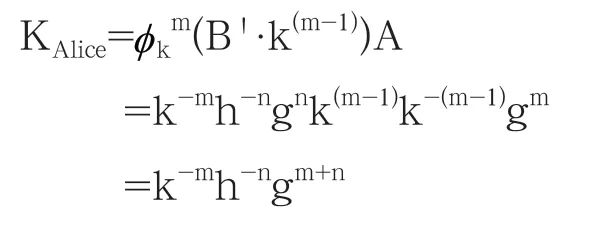
步骤4：Bob计算：

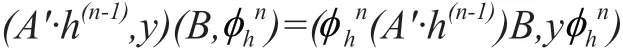
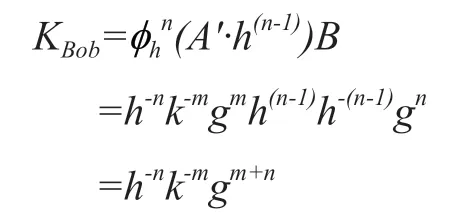
因为h∈G',G'是一个群，所以h-1∈G'，有等式：

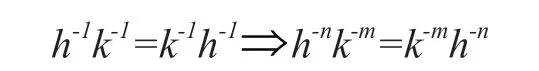
即对于∀m,n∈Z+，h-nk-mgm+n=k-mh-ngm+n,得到

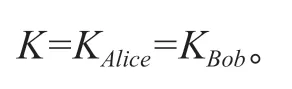
共享密钥为：

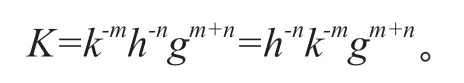
在计算CG(k-1)中，Alice不必算出中心化子CG(k-1)中所有的元素，她只需计算出满足安全要求的元素数量。当Alice发送子群G'给Bob时，她也只发送G'的生成元集合S，即G'=〈S〉。密钥交换流程如图1所示，密钥交换运算量如表1所示。

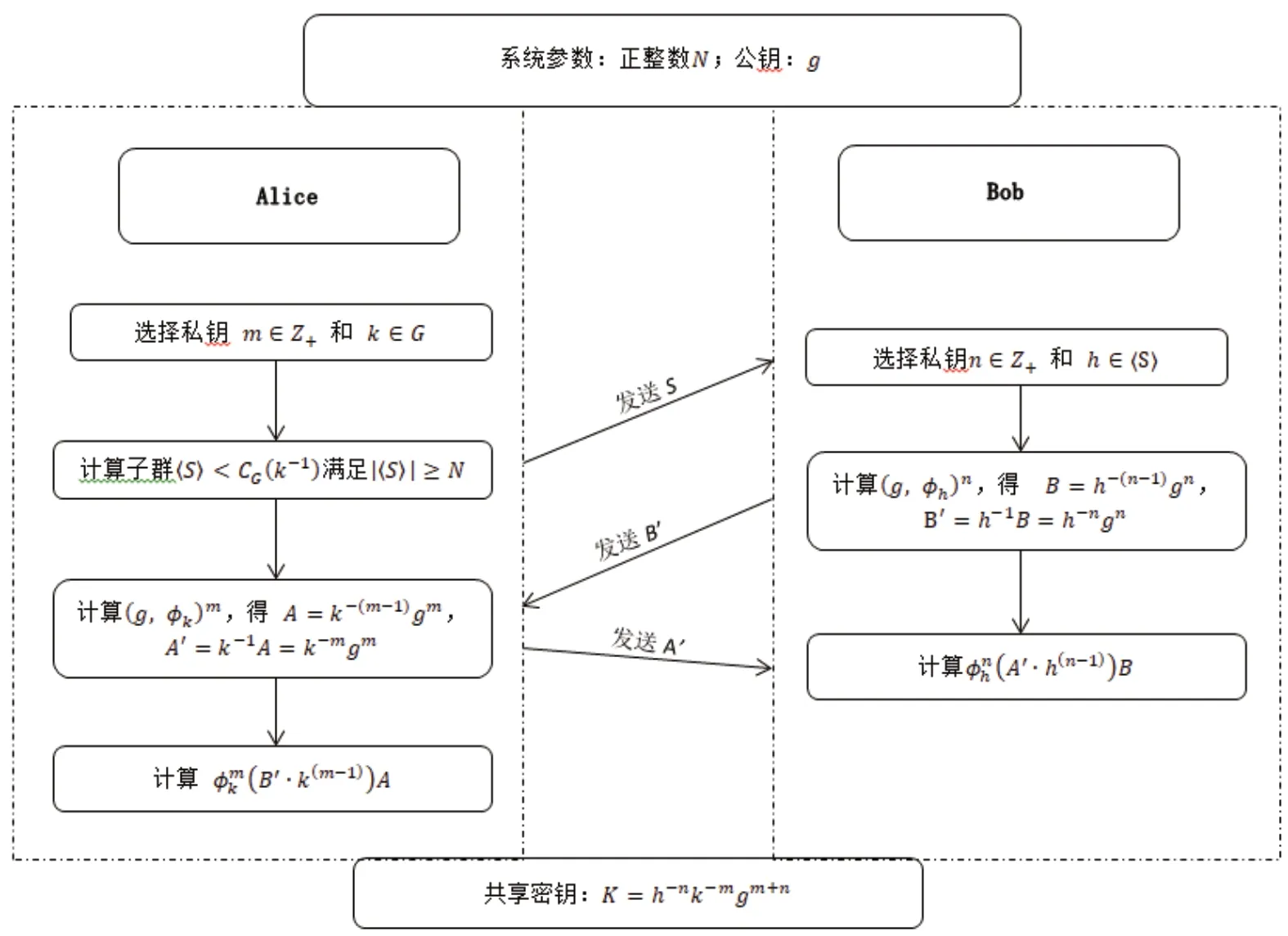
图1 密钥交换协议流程图Fig.1 Flow chart of key exchange protocol

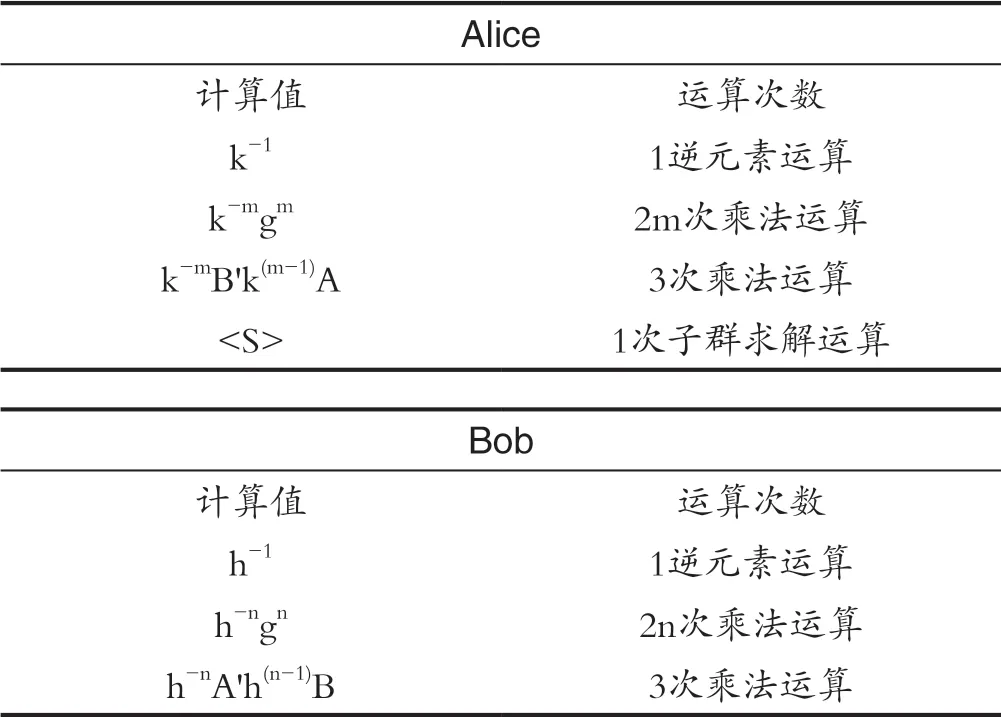
表1 密钥交换协议运算量Tab.1 The amount of computation in the key exchange protocol

3 安全性

本文的密钥交换协议的安全性依赖于无限非交换群上的两个困难问题：等价分解问题(E-DP)和离散对数问题(DLP)。在构建密钥过程中，A'和B'通过公共信道被发送，攻击者可以观察到；而对攻击者来说k-m和h-n是未知的，将他们分别看做一个整体，从A'=k-mgm和B'=h-ngn中计算k-m,h-n,gm,gn就是等价分解问题，计算m和n，攻击者必须解离散对数问题。

Alice和Bob通过公共信道发送信息，攻击者能够观察到传输的协议，并得到一个三元组(g,A'=k-mgm,B'=h-ngn)，他的目的是得到共享密钥K。如果他能从A'中算出k-m和gm，那么共享密钥K=k-mB'gm就能被得到。类似的，如果他能从B'中算出h-n和gn，那么共享密钥也能被得到。这里，仅考虑以上两种情况中的第一种。

3.1 代数攻击

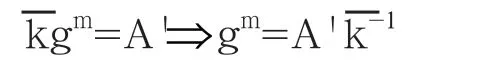
从上式中计算私钥m是一个离散对数问题，因此没有多项式时间算法可以找到m。这样，让A代替gm，得到

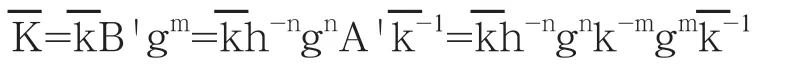
攻击者也可以选择任意一个正整数m∈Z+，让代替m，代替gm，那么有以下等式：

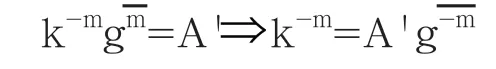
3.2 暴力攻击

暴力攻击意味着攻击者找遍所有可能的密钥。因为k∈G，h∈G'并且G'＜G，所以攻击者从G'入手进行攻击效率更高，即攻击者寻找所有可能的和n∈Z+，满足因为G'＜CG(k)，有N≤|G'|≤|CG(k)|，即至少有N种可能性。假设元素g的阶是γ，那么攻击者必须计算γ次gi(i≤γ)。所以暴力攻击的复杂度介于Nγ和|CG(k)|γ之间。因为G是无限群，可以选择具有足够大的N、|CG(k)|和γ的元素以保证协议的安全性，因此通过暴力攻击获得共享密钥也是不可能的。

引用

[1] Sidel'Nikov V M,Cherepnev M A,Yashchenko V V.Systems of Open Distribution of Keys on the Basis of Noncommutative Semigroups[J].Doklady Mathematics,1993,48(2):566-567.

[2] SHPILRAIN V,USHAKOV A.A New Key Exchange Protocol Based on the Decomposition Problem[J].Contemp.Math.Amer.Math.Soc,2005,172(2):161-167.

…………

[3] Ko K H,Sang J L,Cheon J H,et al.New Public-Key Cryptosystem Using Braid Groups[C]//Annual International Cryptology Conference.Springer,Berlin,Heidelberg,2000.

[4] MYASNIKOV A D,USHAKOV A.Quantum Algorithm for the Discrete Logarithm Problem for Matrices Over Finite Group Rings[J].Group Complexity Cryptology,2014,6(1):31-36.

[5] SHPILRAIN V,USHAKOV A.The Conjugacy Search Problem in Public Key Cryptography:Unnecessary and Insufficient[J].Applicable Algebra in Engineering Communication&Computing,2006,17(3-4):285-289.

[6] SAKALAUSKAS E,TVARIJONAS P,RAULYNAITIS A.Key Agreement Protocol (KAP) Using Conjugacy and Discrete Logarithm Problems in Group Representation Level[J].Informatica,2007,18(1):115-124.

[7] HABEEB M,KAHROBAEI D,KOUPPARIS C,et al.Public Key Exchange Using Semidirect Product of(Simi)Groups[J].Cryptology and Information Security Series,2013:226-237.