杂交粒子群算法在含模糊价值评判的旅游线路优化中的应用*

阳光学院基础教研部 俞超群

针对粒子群算法在求解时容易早熟收敛，搜索得到最优解的能力差，引入遗传算法中的杂交思想，采用改进后的粒子群算法，应用对福州市10个景点的旅游线路的规划，结合不同旅游价值取向的游客，将杂交粒子群算法应用到含模糊价值评判的旅游线路的优化研究中去。通过仿真实验，验证了该算法理论运用于旅游线路能有效提高寻优的效率，给游客及旅行社一个比较合理的意见和建议。

随着社会经济的发展，近年来，周边游逐渐成为福州人的旅游线路的首选，旅游线路的设计和优化，是各个旅行社以及游客关注的问题所在，节约时间成本，优化旅行距离，是旅行线路选择的一个关注点。考虑到游客的旅行价值偏好[1]，文献[1]将模糊评价引入遗传算法理论，建立基于遗传算法的旅行线路优化算法，设计出既满足追求最少的路程时间消耗和又满足游客最大的旅游价值的旅行线路。但遗传算法编码复杂，收敛速度慢，导致寻优过程耗时较长。粒子群算法[2]（PSO）是对鸟类觅食行为这样一个简单的社会系统进行模拟,通过迭代的形式进行全局优化的一种群体智能算法，目前已经开始应用于诸多领域[3-5]，其在优化问题上的研究已经逐渐被人们重视，但是如果优化问题的搜索空间大，粒子群算法在求解时容易早熟收敛，不容易得到最优解。杂交粒子群算法[6]由Angeline提出，将遗传算法中杂交的概念引入到粒子群算法中，是对粒子群算法的一种改进，把个体粒子的交叉、变异操作引入到粒子群的结构当中，该算法保留了粒子间的差异，同时其在收敛性和鲁棒性都优于标准粒子群算法。本文采用杂交粒子群算法，结合模糊评价理论[7]，建立基于杂交粒子群算法的旅游线路的优化算法，充分发挥遗传算法和粒子群算法的优势，以期选择的线路既满足实现最少的路程时间消耗，又能给予游客最大的旅游价值体验。

1 旅游线路优化问题描述

旅游线路选择问题是指具有一定价值偏好的游客从追求最小的路程时间消耗和满足最大旅游价值感出发，在选定的一组景点中选择合适的起点进行遍历。为了便于进行比较，采集的景点坐标和价值偏好均采用文献[1]的数据，在百度地图上选定10个景点，采集景区坐标，针对景点的景观属性和游客的主观感受构造综合评判矩阵，得到各个景点的模糊综合评价[1]。每个景区的坐标、对应序号以及旅游价值如表1所示。

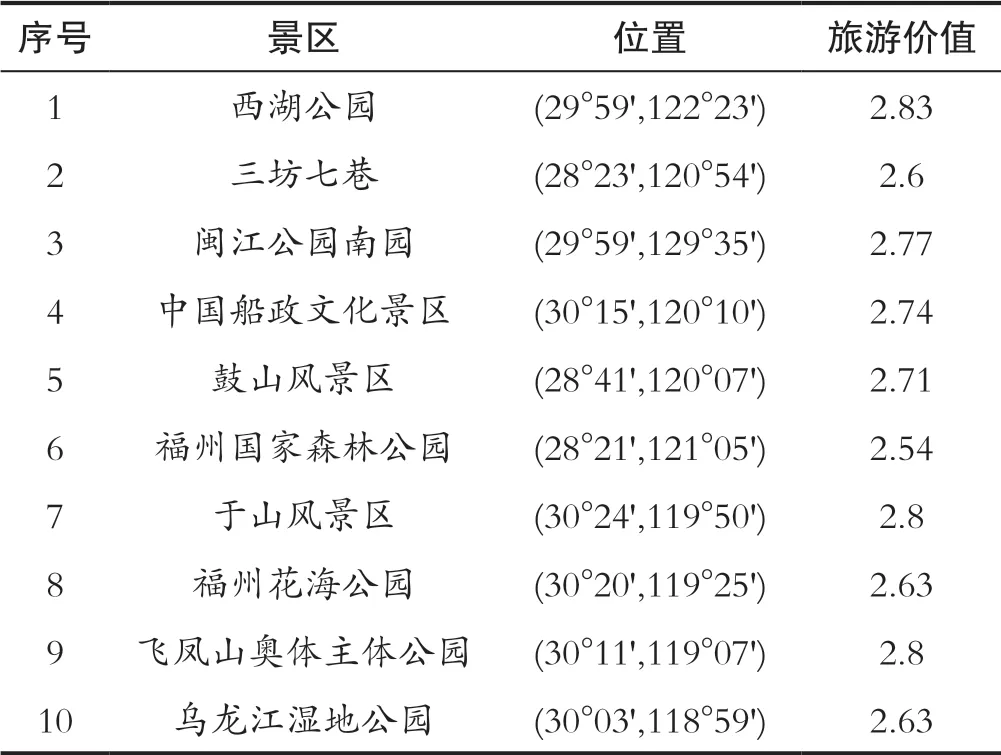
表1 10个景区位置的数字序号、位置和旅游价值Tab.1 Number, location and tourism value of 10 scenic spots

文献[1]中单独利用遗传算法进行求解可以实现旅游价值的优化，但收敛速度慢，寻优过程耗时较长。

2 粒子群算法和杂交粒子群算法简介

粒子群优化算法[2]是于1995年首次提出来的一种在全局范围内搜索最优解的群体智能算法，根据目前广泛使用的标准粒子群算法的流程，该算法的数学思想是：设m维空间中有popsiz个粒子，第i个粒子在时刻t的位置为

群体最优位置（全局极值）为gbestt=[g1,g2,…,gm]T，

所有的粒子都通过追寻个体极值和全局极值在这个群体空间中飞行以找到最优解。其速度和位置的更新的数学表达式如下所示：

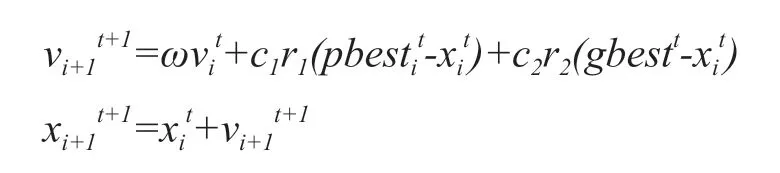
其中，ω为惯性权重系数，c1，c2为学习因子。

算法通过maxiter次迭代得到最优解，也就是将最大迭代次数作为算法的终止条件。

作为粒子群算法中最重要参数的惯性权重系数，其数值的大小决定了算法的全局和局部搜索能力的强弱，分别提出了自适应权重法、随机权重法、线性递减权重法。戴文智,杨新乐于2015年提出了惯性权重对数递减的粒子群优化算法[8]。为了提高算法的收敛速度，王玉燕,李帮义,申亮将算法迭代公式中个体粒子的速度项去掉，保留位置更新公式，并将惯性权重系数放在位置矢量上，这样算法迭代公式由二阶降为一阶微分方程，能有效提高算法收敛速度[9]。文献[10]中，谭皓和王金岩等将粒子群算法和蚁群算法这两种不同设计的杂交算子，通过模拟自然界中的物种在不同种群间的协作和交流，将杂交粒子选择机制引入到粒子群结构中，提高算法的寻优能力，这也为粒子群算法改进给予启发。

传统PSO算法容易出现粒子收敛于一个非最优解后，无法跳出来导致搜索停止。为了解决这个问题，本文在进行旅游线路寻优，采取了基于杂交机制的粒子群算法[4]，该算法是借鉴遗传算法中杂交的概念，选择一定数量的粒子放入杂交池内，将个体和最优个体或个体和群体最优的粒子进行杂交，完成粒子间的信息交换，提高寻优能力。子代位置由父代位置以一定的概率交叉得到c(x)=kp1(x)+(1-k)p2(x)，其中c(x)为子代个体的位置，p1(x),p2(x)父代个体的位置，k在[0,1]上服从均匀分布，子代个体的速度

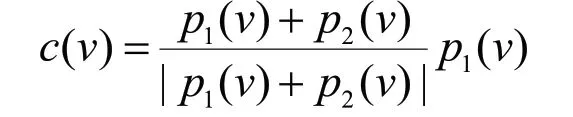
其中p1(v),p2(v)父代个体的速度。

3 杂交PSO算法对于旅行线路优化求解设计

杂交PSO算法对旅行线路优化求解设计的算法流程如图1所示，根据图1中杂交PSO算法对旅行线路优化求解设计的算法的流程图所示，具体步骤如下：

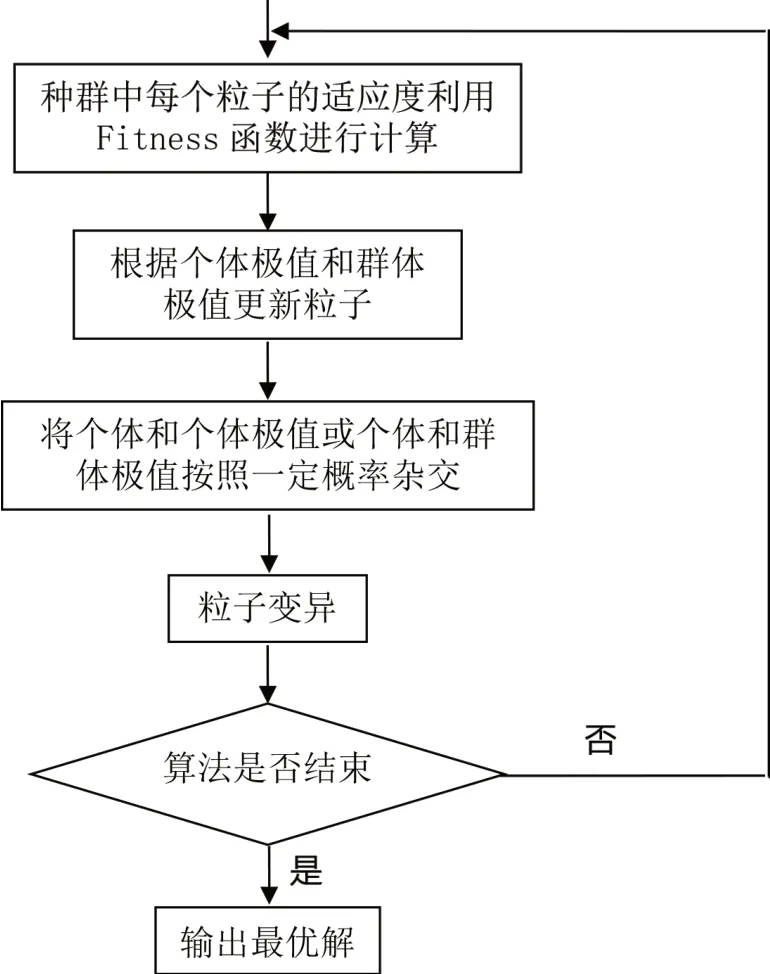
图1 杂交PSO算法对旅行线路优化求解设计的算法流程Fig.1 The algorithm flow of the hybrid PSO algorithm for the optimal solution design of the travel route

(1)对粒子群进行初始化，设置各个粒子的位置，群体规模和迭代次数。粒子的编码采用整数编码的形式，每个粒子表示遍历的10个景区的路线，比如粒子编码为[1,2,3,4,5,6,7,8,9,10],表示从西湖公园开始，三坊七巷，闽江公园南园，船政文化景区，中国鼓山风景区，福州国家森林公园，于山风景区，福州花海公园，飞凤山奥体主体公园这样的一条路线。

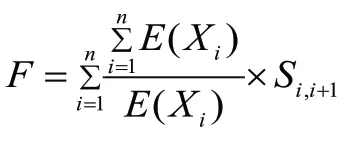
(3)将每个粒子的适应度和个体极值进行比较，更新个体极值pbesti。

(4)比较当前所有的pbesti，更新gbest。

(5)将粒子和个体极值、群体极值进行交叉，按一定的概率选择两个位置，然后把粒子和个体极值或者粒子和群体极值进行交叉，产生新的个体粒子，如果新的个体粒子中存在重复位置，则将个体粒子中未包括的景区序号代替重复的景区序号。

(6)对自身进行变异，随机选择个体粒子中的两个位置，进行互换，如果变异后的个体粒子优于原来的粒子，才保留，否则放弃。

(7)判断是否满足算法终止条件，满足则停止搜索，如果不满足，则返回步骤（3）。

(8)输出最终结果。

4 仿真结果

在程序中，种群规模我们取为20，总共进行100次迭代。适应度值变化情况如图2所示，可以看出，杂交PSO算法具有较强的收敛能力，较快得到全局最优解。

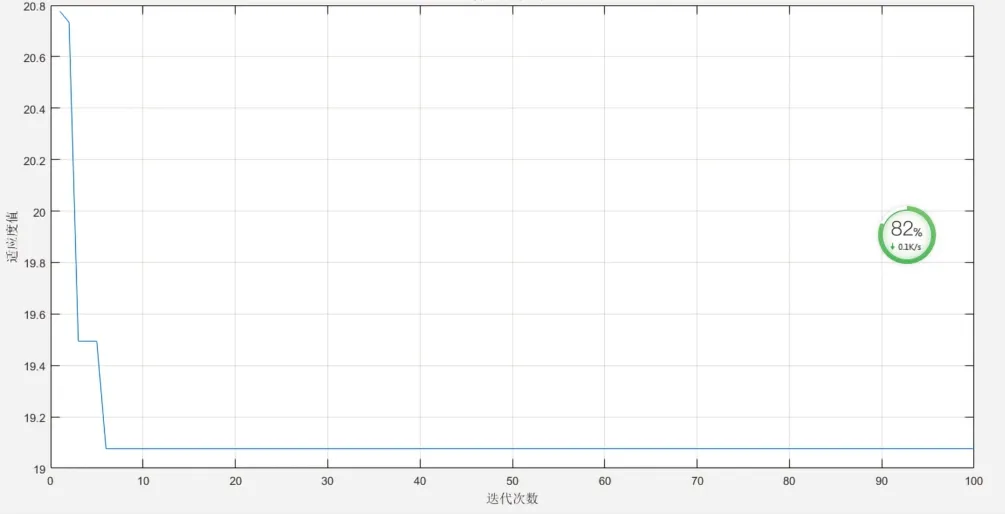
图2 适应度值变化Fig.2 Changes in fitness value

综合考虑游客的价值偏好和最大效率的路线规划，如图3所示，游客可以选择乌龙江湿地公园—于山风景区—中国船政文化景区—福州国家森林公园—闽江公园南园—西湖公园—三坊七巷—鼓山风景区—飞凤山奥体公园—福州花海公园。

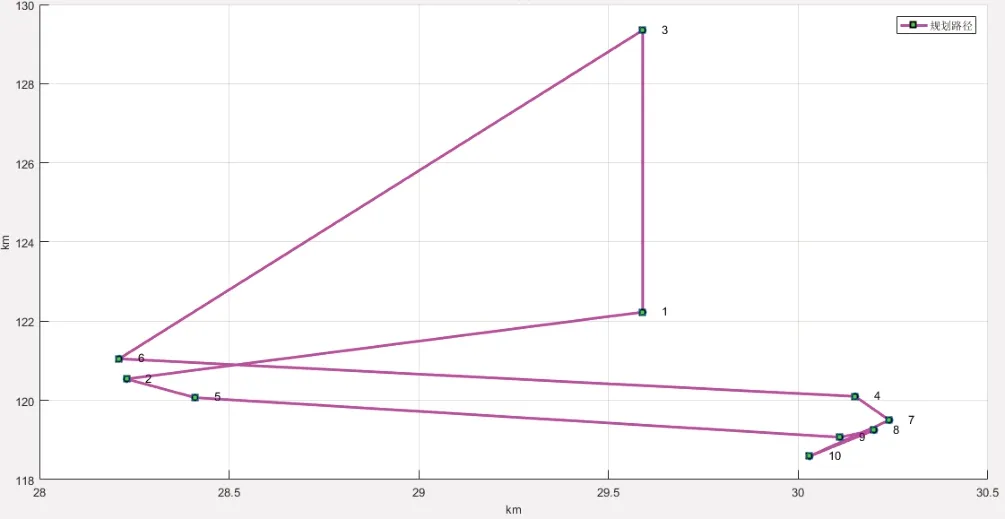
图3 种群中10个景点的路线优化方案Fig.3 Route optimization scheme for 10 scenic spots in the population

5 结论

在旅游线路选择问题上，既要考虑优化旅行距离和时间，使得效率最大，又要考虑游客的旅行价值偏好，在智能算法中遗传算法编码复杂，寻优过程耗时长，在求解最优解时，存在收敛速度慢，局部搜索能力差等缺点，本文提出了基于杂交机制的粒子群算法，并结合游客对于景点的模糊评价，设计出完善可行的旅游线路。经过实验仿真，验证了该算法理论运用于旅游线路能有效提高寻优的效率，给游客及旅行社一个比较合理的意见和建议。但是，对于景点的评价方式，还是比较标准化，评价手段比较单一，在应用中还要寻求更灵活的评价方式，以期能广泛应用于旅游线路的规划和设计。

引用

[1] 俞超群.基于模糊综合评判和遗传算法的旅游线路的优化[J].宁德师范学院学报(自然科学版),2018,30(2):171-175+181.

[2] 杨明轩.粒子群算法的改进及应用研究[D].岳阳:湖南理工学院,2020.

[3] 张津源.基于改进粒子群算法的物流路径规划研究[D].哈尔滨:哈尔滨师范大学,2021.

[4] 邢晓溪.粒子群算法研究进展[J].数据通信,2015(3):19-21+30.

[5] 赵先章,常红星,曾隽芳,等.一种基于粒子群算法的移动机器人路径规划方法[J].计算机应用研究,2007(3):181-183+186.

[6] 黄炜霖,刘建军,张明,等.带有退火和杂交变异思想的改进粒子群算法[J].计算机工程与应用,2015,51(19):43-49.

[7] 徐永琳,王斐然.基于多因素模糊综合评价的最优旅游线路分析[J].湖北民族学院学报(自然科学版),2014(1):81-84.

[8] 戴文智,杨新乐.基于惯性权重对数递减的粒子群优化算法[J].计算机工程与应用,2015,51(17):14-19+52.

[9] 王玉燕,李帮义,申亮.TPT-CLSC的协调研究[J].中国管理科学,2007(05):101-106.

[10] 谭皓,王金岩,何亦征,等.一种基于子群杂交机制的粒子群算法求解旅行商问题[J].系统工程,2005(04):83-87.