针对复杂噪声场景的FCM聚类算法非局部改进*

聊城大学数学科学学院 吕美琪 韩红燕 刘婷婷 孙忠贵

作为一种常用的图像分割算法，模糊C均值聚类(FCM)对噪声过于敏感。针对此缺陷，研究者们提出了诸多改进算法。然而，现有算法在面对较为复杂的噪声场景时，所得图像分割效果往往不令人满意。通过对经典FCM算法的目标函数施加非局部正则化，该文给出一个FCM非局部改进算法(FCM_UNL)。在复杂噪声场景下进行图像分割时，FCM_UNL能保持较高的分类精度。初步的图像分割实验表明了所提算法的有效性。

图像分割是图像处理的关键内容之一，分割质量的好坏往往对后续的图像识别、分析等环节有着直接影响[1,2]。因此，图像分割一直是计算机视觉领域的研究热点之一。而聚类算法则是一类常用的图像分割工具[3,4]。与传统聚类非此即彼的硬划分相比，模糊C均值聚类(Fuzzy C-Means，FCM)[5]充分利用了模糊理论在类别描述上的灵活性，克服了硬划分的缺陷，能更灵活地反映现实事物的类属关系，从而有可能取得更好的图像分割效果。FCM的相关研究也吸引着众多科研工作者的关注。

目前FCM用于图像分割的具体研究主要集中在单一高斯噪声，而实际的图像获取过程往往会受到更为复杂噪声的影响，因此开展复杂噪声场景下的FCM图像分割研究更具有实用价值。近年，在图像增强领域已有了一些关于复杂噪声去除的相关研究[6,7]。文献[6]通过重新定图像块的相似度量，设计出一个通用的非局部滤波算法(Universial NonLocal Means，UNLM )，UNLM不但能滤除高斯噪声，还能滤除脉冲噪声及高斯与脉冲两者的混合噪声。受文献[6]工作的启发，本文拟对FCM开展通用的非局部改进，以增强其在复杂噪声场景下图像的分割性能。

本文第1节对FCM及一些现有的改进算法进行总结，并指出这些算法各自的优、缺点，说明它们面对复杂噪声场景，图像分割性能下降的主要原因。结合第1节的分析，第2节给出一个FCM算法的通用非局部改进模型，并通过模型求解，使改进算法得到具体实现。第3节给出本文相关算法的图像分割仿真实验，测试所提算法有效性。最后总结全文，并对未来值得进一步研究的方向进行初步探讨。

1 经典FCM及现有改进算法

1.1 经典FCM算法

令X={x1,x2,…,xn}表示有n个像素点的图像，其中xi为第i个像素的灰度值，则经典FCM算法为了把图像分割为c类定义如下目标函数：

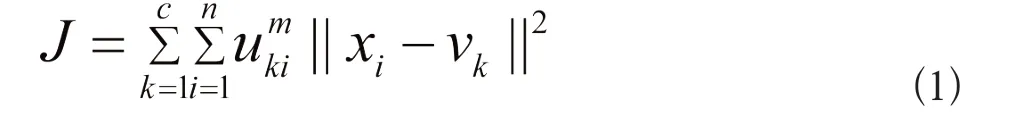
约束条件为：

在上式中||·||为欧几里得范数，m(m＞1)为模糊参数。通过拉格朗日乘子法对Jm求最小值，隶属度与聚类中心如下：

通过选取初始聚类中心，对(3)式进行迭代优化，得到各聚类中心的隶属度，从而完成对图像X的分割。

1.2 现有改进算法

经典FCM算法对噪声十分敏感，在对含噪图像进行分割时往往不能获得理想效果[5]。为弥补FCM算法的这一缺陷，研究者们开展了一系列工作：

以邻域像素构成正则项，通过对FCM目标函数施加空域正则化约束，文献[8]提出了FCM_S算法，其目标函数如下：

其中β为正则化参数，Si为第i个像素的邻域，SR为相应领域中像素的数量。FCM_S较传统FCM算法在图像分割中对噪声的鲁棒性明显提高。然而，由于FCM_S算法涉及大量邻域计算，较FCM算法运算复杂度增加十分明显。为提高FCM_S的运算效率，文献[9]提出FCM_S1与FCM_S2算法，分别用均值滤波（FCM_S1）或中值滤波（FCM_S2）取代FCM_S中的邻域计算，先得到一幅滤波图像，然后以此滤波图像为参考图像，并将其与目标图像相结合进行图像分割。在保证对噪声鲁棒性的同时，FCM_S1与FCM_S2算法在运算速度方面较FCM_S有了明显提升。

其中FCM_S1与FCM_S2的目标函数分别为：

上面目标函数中α为正则化参数，与别为第i个像素的均值与中值滤波输出。

非局部均值滤波器(NonLocal Means，NLM)[10]由于更好地利用了图像的周期性，取得了较传统滤波算法更优秀的去噪效果，并在图像增强领域得到广泛应用[11-13]。受NLM算法的启发，文献[14]将NLM滤波取代FCM_S1算法中的局部均值滤波得到一个非局部的FCM改进算法，并称之为FCM_NLS，其目标函数相应化为：

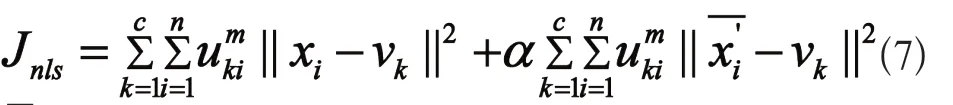
需注意，上述这些对FCM的改进算法主要是针对单一高斯噪声，且污染强度不高的情况。考虑到实际的图像获取图像过程往往会受更为复杂噪声的污染(如强噪声或混合噪声)。如何使FCM算法能在复杂噪声场景保持好的图像分割性能就变得很有意义。

2 FCM非局部改进算法(FCM_UNL)

在图像增强领域，已有一些利用非局部策略对复杂噪声进行滤除的工作[6,7]。其中文献[6]提出的通用非局部滤波器(UNLM)在滤除强高斯噪声及高斯、脉冲混合噪声时均取得了较好效果。在UNLM中像素i与像素j间权值wij获取步骤如下：

算法开始：初始化最小图像块边长dmin，最大图像块边长dmax

(1)d=dmin;

(2)若d≤dmax，计算匹配块中可信像素的指标集KU[6]，否则转（6）;

(3)若j∉KU，转(6);

(4)若KU＜T则d=d+1，转(2)；(T为可信阈值，默认为15)

(6)wij=0；

算法结束。

与NLM类似，UNLM在本质上依然是一个加权滤波器，其中第i个像素的滤波输出为。将此滤波输出用于FCM算法的非局部正则化约束，得到改进算法FCM_UNL的数学模型：

相应拉格朗日函数为：

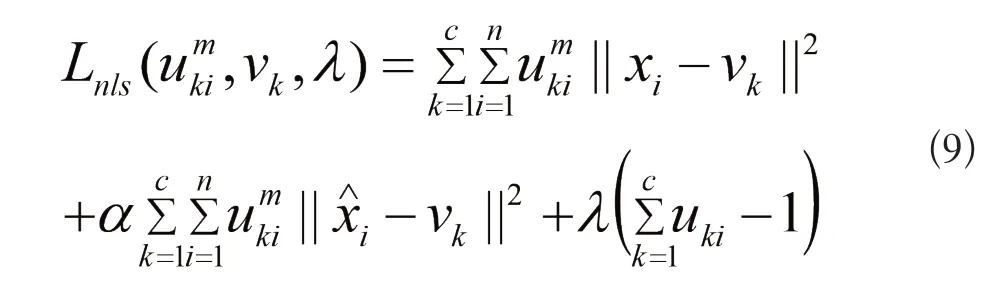
分别令

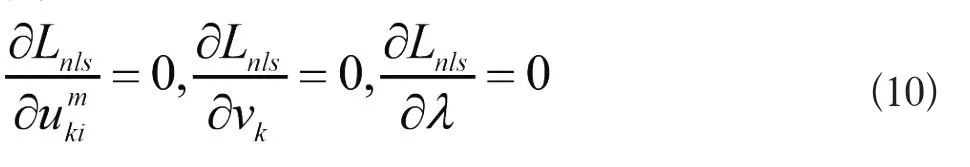
得

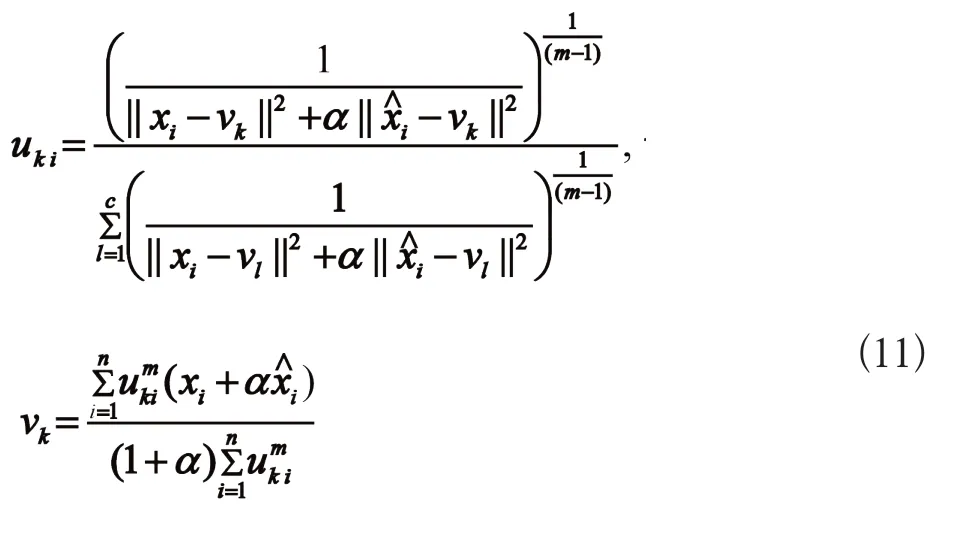
从而得到FCM_UNL模型的解。

3 实验仿真

实验采用一幅人工合成图像，首先对图像施加不同程度的高斯噪声、高斯与脉冲混合噪声，然后进行分割实验，从分割精度(Clustering Accuracy, CA)[15]与视觉效果两个方面进行实验结果比较。其中脉冲噪声强度用方差σ表示，脉冲噪声强度用r表示。分割精度CA采用下式计算：

其中C为类别总数，Ai是分割算法得到的第i类的像素集，Ci为第i类像素的正确参照，|·|为相应集合中元素的数量。

在具体实验中，本文所提FCM_UNL算法的正则化参数α取值为6，图像块的搜索边长从dmin=4到dmax=6，搜索窗边长为21。考虑到实际中噪声类型、强度等往往为未知数，为增强算法的实际应用，FCM_UNL在进行非局部滤波时，受文献[14]启发，FCM_UNL中高斯核参数h固定为30，不再依赖具体噪声类型及强度。实验中其余算法的参数选择均依照原始文献。

图 1 高斯噪声σ = 50 时人工合成图像分割的视觉效果Fig.1 Segmentation results on the synthetic corrupted byGaussian noise with σ=50

3.1 单一高斯噪声情况

对一幅人工合成图像施加不同强度高斯噪声，然后采用不同算法进行图像分割，各算法对图像的分割精度如表1所示。其中σ=50时分割视觉效果如图1所示。

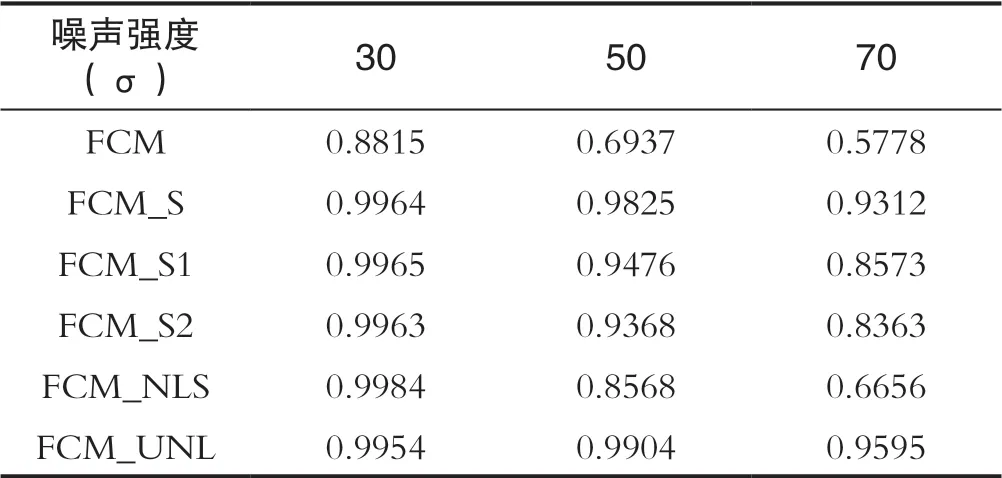
表1 不同强度高斯噪声下人工合成图像分割精度（CA）Tab.1 Segmentation accuracy of synthetic image under different intensity Gaussian noise(CA)

由上述实验结果可以看出，对单一高斯噪声环境，随噪声强度的增加(方差大于30)，本文所提算法(FCM_UNL)在所有比较算法中均取得最高的分割精度与最好的视觉效果。

3.2 混合噪声情况

对图像施加不同程度的混合噪声，不同算法的分割精度如表2所示。

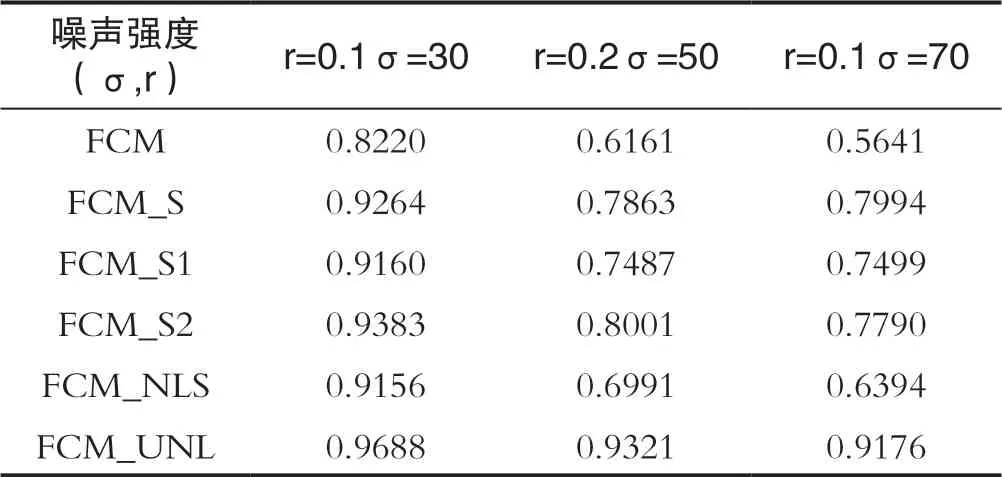
表2 脉冲与高斯混合噪声下人工图像的分割精度（CA）Tab.2 Segmentation accuracy of artificial image under impulse and Gaussian mixture noise(CA)

当r=0.2，σ=50时的视觉效果如图2所示。

4 结论

本文对经典FCM算法的目标函数施加通用非局部正则化空域约束，提出了一个FCM的改进算法(FCM_UNL)，并将其用于图像分割任务。FCM_UNL算法克服了现有一些FCM改进算法只能处理单一噪声的缺陷，仿真实验表明，相对于一些现有改进算法，FCM_UNL在复杂噪声场景下依然能够取得良好的图像分割效果。需注意的是，如同FCM_NLS算法，本文提出的FCM_UNL算法由于实现过程中要进行非局部滤波，这使得其运行速度较一些局部正则化改进算法有所降低。因此，如何提升对FCM_UNL算法的运算速度，将值得进一步开展研究。

图 2 混合噪声为r=0.2σ=50时人工合成图像分割的视觉效果Fig.2 Segmentation results on the synthetic corrupted bymixed noise with r = 0.2 and σ=50

引用

[1] LEI T,JIA X H,ZHANG Y N,et al.Superpixel-based Fast Fuzzy C-means Clustering for Color Image Segmentation[J].IEEE Transactions on Fuzzy Systems,2018,27(9):1753-1766.

[2] 林开颜,吴军辉,徐立鸿.彩色图像分割方法综述[J].中国图象图形学报:A辑,2005,10(1):1-10.

[3] 李旭超,刘海宽,王飞,等.图像分割中的模糊聚类方法[J].中国图象图形学报,2012,17(4):447-458.

[4] 王晓飞, 郭敏. 结合模糊 C 均值聚类与图割的图像分割方法[J].计算机应用,2009,29(7):1918-1920.

[5] DUNN J C. A fuzzy relative of the ISODATA Process and Its Use in Detecting Compact Well-separated Clusters[J].Journal of Cybernetics,1973,3(3):32-57.

[6] SUN Z G,CHEN S C.Modifying NL-means to a Universal Filter[J].Optics Communications,2012,285(24):4918-4926.

[7] XIONG B,YIN Z.A universal denoising framework with a new impulse detector and nonlocal means[J].IEEE Trans.on Image Proc essing,2012,21(4):1663-1675.

[8] AHMED M N,YAMANY S M,MOHAMED N,et al.A Modified Fuzzy C-means Algorithm for Bias Field Estimation and Segmentation of MRI Data[J].IEEE Trans.on Medical Imaging,2002,21(3):193-199.

[9] CHEN S C, ZHANG D Q.Robust Image Segmentation using FCM with Spatial Cnstraints Based on New Kernel-induced Distance Measure[J].IEEE Trans. on System,Man,and Cybernetics.Part B:Cybernetics,2004,34(4):1907-1916.

[10] BUADES A,COLL B,MOREL J M.A Nonlocal Algorithm for Image Denoising[C]//In Proc.Int.Conf.Computer Vision and Pattern Recognition (CVPR),2005,2:60-65.

[11] BUADES A,COLL B,MOREL J M.Image Denoising Methods a New Nonlocal Principle[J].SIAM Review:Multiscale Modeling and Simulation,2010,52(1):113-147.

[12] ROUSSEAU F.A Non-local Approach for Image Super-Resolution Using Intermodality Priors[J].Medical Image Analysis,2010,14(4):594-605.

[13] XU Q,JIANG H L,SCOPIGNO R,et al.A New Approach for Very Dark Video Denoising and Enhancement[C].International Conference on Image Processing,2010:1185-1188.

[14] ZHAO F,JIAO L C,Liu H Q.Fuzzy C-means Clustering with Non Local Spatial Information for Noisy Image Segmentation[J].Frontiers of Computer Science in China,2011,5(1):45-56.

[15] WU M R,SCHOELKOPF B.A Local Learning Approach for Clustering[C]//In Proc.20th Annual Conference on Neural Information Processing Systems,2007,1529-1536.