大规模复杂疾病基因组交互网络嵌入算法*

北方工业大学 刘海煜 史岩 刘林涵

复杂基因组网络往往具有大量的节点和边，学习其节点特征并应用于一些下游任务如链路预测往往不那么容易。因此，对比找到一种合适的嵌入算法以提高对复杂基因组网络的嵌入效率同时更好的应用于一些下游任务成为了一个非常有意义的问题。本文采用三种常用的嵌入算法（DeepWalk，Line，Node2vec）对复杂基因组网络进行嵌入学习得到节点的低维向量表示，然后将其应用于链路预测任务。同时重新定义了评估指标Micro-F1的各项参数，经过实验后发现DeepWalk对于复杂基因组网络的链路预测更为适用。

任何复杂的系统都以网络的形式出现。而网络数据往往是复杂的，处理起来具有挑战性。为了有效地处理网络数据，关键是寻找有效的网络数据表示[1]。人们致力于开发新型网络嵌入[2]。文献[3]提出了DeepWalk算法。文献[4]提出的LINE算法。文献[5]提出的Node2vec算法。

链路预测是网络分析中一个重要的应用。链路预测主要是基于已知的网络预测网络中隐藏的链路或未来即将产生的链路。基于共同邻居相似性指标主要有余弦相似性[6]、Adamic指标[7]等。随着深度学习、神经网络在文本处理、图像理解等领域的成功应用，将神经网络应用于链路预测成为目前研究的重点。

然而在以往的研究中对复杂基因组网络的嵌入和链路预测任务还研究甚少。

复杂疾病是指由众多因素共同作用下发生的疾病，主要包含高血压、糖尿病等疾病。当前对于复杂疾病的研究主要采用大规模基因组关联分析。但该方法存在没有充分考虑基因交互、运行效率低等问题。为此本文通过三种嵌入算法对复杂基因组网络进行嵌入得到低维向量表示并进行链路预测。主要贡献如下：

(1)第一次完成复杂基因组网络的链路预测任务。

(2)重新定义了Micro-F1参数使得其能更好的评估边级预测性能。

(3)对比了三种算法在复杂基因组网络上的链路预测性能，得出DeepWalk在复杂基因组网络可以取得更优预测性能的结论，同时发现Line模型更适用于大规模图。

1 模型介绍及相关定义

对于复杂基因组网络G={V,E}，其中，V为SNPS节点集，且V={v1,v2,…,v|v|}，|V|为节点总数；E为网络中链接集，且ei,j∈E表示SNPS节点vi和SNPS节点vj之间存在链接关系。

1.1 DeepWalk模型

DeepWalk主要包括两个部分：随机游走生成器和更新过程。首先DeepWalk采用Random Walk在网络中进行截断的随机行走，生成一组行走序列。算法定义以顶点vi为根的随机游走为Wvi。随机游走生成器就是一个由随机变量Wvi1,Wvi2,…,Wvik组成的一个随机过程。对于每个行走序列，采用Skip-Gram模型，DeepWalk的目标是在该行走序列中最大化节点vi的条件概率，如下：

其中w是窗口大小，(vi)代表着vi当前位置，{vi-w,…,vi+w}vi是vi的上下文节点。

对于序列中的每个顶点，计算条件概率，并借助梯度下降算法更新结点的向量表示。

1.2 Node2vec模型

Node2vec定义了灵活的节点网络邻居的概念，并设计了一种对领域节点进行采样的二阶随机遍历策略。Node2vec定义了俩个参数p和q来实现有偏向的随机游走。考虑一个随机游走刚经过边(t,v)，并正处于顶点v。随机游走需要决定下一步，所以需要计算从顶点v经过边(v,x)的转移概率πvx。定义转移概πvx=αpq(t,x)·ωvx。

Node2vec能够密切学习具有相同网络邻居的节点形式。同时一些实验[5]也证明Node2vec算法是一种高度稳定的学习特征的算法，可以在不同类型的网络都提供最佳性能。

1.3 Line模型

Line主要用于大规模图嵌入，它能够保持一阶和二阶相似性。

一阶相似性对于每个边(i,j)，定义节点vi和节点vj的联合分布概率为：

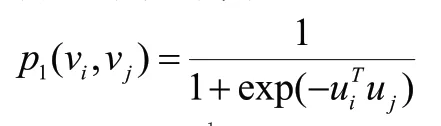
其中ui∈Rd是顶点vi的低维向量表示。(一阶相似性只适用于无向图)二阶相似性对无向图和有向图都是适用的，对于一个边(i,j)定义它的转移概率如下：

其中|V|是节点数量。对于每一个顶点vi，上式定义了一个在整个网络顶点集上的条件分布P2(·|vi)。Line模型可以很容易地扩展到具有数百万个顶点和数十亿条边的网络[4]。

2 链路预测(Link Prediction)实现

网络中的链路预测是指如何通过已知的网络节点以及网络结构等信息预测网络中尚未产生连边的两个节点之间产生链接的可能性。基于Embedding的链路预测是通过嵌入算法学习后得到的节点低维向量表示来估计节点间的相似性度量。以此来预测节点之间是否可能存在联系。

具体做法是对得到的Embedding向量表示进行处理，用两个节点的欧式距离大小来评估两个节点之间的联系程度。

对于两个节点vi和vj的n维向量表示X和Y，vi和vj的欧式距离d为：

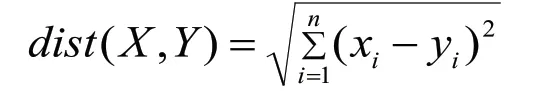
为了更好的进行链接预测，采用K-NN的思想保留欧式距离TOPK的边。

2.1 K-NN算法

设对象x={x1,…,xn}，xi(1≤i≤n)是它的特征值。x是n维特征空间D=(D1,…,Dn)上的一点，x,y∈D，则x，y在特征空间F上的距离为dF(x,y)。

K-NN算法定义了一个下界d'和上界d''，设特征子空间，F1=(D1,…,Dk),k≤n，则围绕x计算dD(x,y)的过程中：

(1)如果dF1(x,y)≤d'，进一步计算dD(x,y)是不必要的，因为必有dD(x,y)≤d'，一定不会满足条件。

(2)如果dF1≥d''，进一步计算dD(x,y)是不必要的，因为必有dD(x,y)≥d''，一定不满足条件。

这样基于K-NN算法可以减少大量无用的计算，提高预测效率。

2.2 基于K-NN算法的欧氏距离TOPK计算

采用K-NN算法的思想设置阈值dmin和dmax，维护一个TOPK的队列保存欧式距离最大的前k个节点对，同时队列内的每一对节点(vi0,vi1)满足：

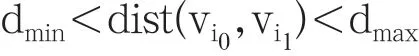
其中dmin和dmax计算方法如下：

从测试集中每次随机抽取10%的数据，计算出欧式距离最小值和最大值分别为dmini和dmaxi，总共取n次，则：

2.3 链路预测评估方法

Micro-F1分数可以很好的表示节点分类性能的好坏，基于节点分类的参数设定，定义用于评估链路预测的Micro-F1参数如下：

TP：预测的边在测试集中

TR：预测的边可能存在

FP：预测的边不可能存在

FN：预测的边在训练集中

则精准率Precision:

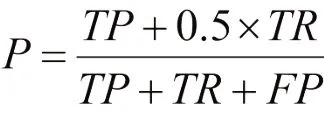
召回率Recall:

这三个指标可以很好的反应链接预测的好坏。

3 实验

实验选用HT(x2＞30)，HT(x2＞35)和HT(x2＞40)三个高血压疾病交互网络数据集，数据集的具体参数如表1所示。

对比DeepWalk，Line和Node2vec三个模型在复杂基因组网络中链接预测性能。实验过程中取数据集70%的点作为训练集，30%的点作为测试集，采用精准率P，召回率R和Micro-F1三个指标。在不同数据集下，三种模型对比数据如表2所示。

实验表明，DeepWalk在不同数据集下都取得了最好的召回率和Micro-F1分数,在HT(x2＞40)中准确率取得最优。Line在三个数据集上都取得了良好的准确率表现，但召回率普遍较低，且各项评估指标在数据集规模较大时能够取得更好的效果。Node2vec模型在三个数据集中表现介于两者之间，且在数据规模较小时，与DeepWalk性能差距较大，随着数据集变大与DeepWalk性能差距逐渐减小。

在不同数据集下，DeepWalk均取得了最优的效果，而Line在数据量较大的数据集中准确率取得了较好的成绩，Node2vec总体表现优于Line，在大规模数据集中接近与DeepWalk。由于DeepWalk采用随机游走的方法学习节点的特征表示，可以在图规模较大的时候有效减少计算量。综上所述，DeepWalk在复杂基因组网络取得了更优的预测效果，Line模型适用于较大规模图的预测。

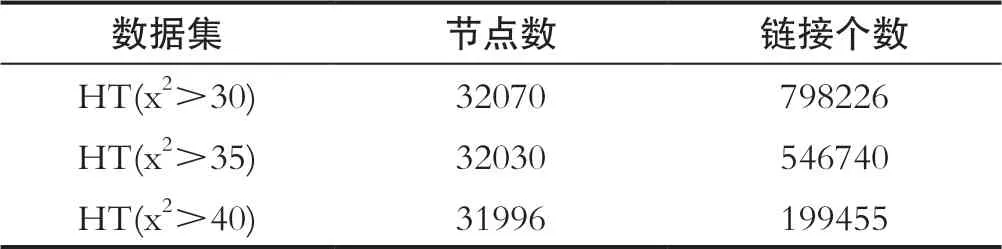
表 1 数据集参数Tab.1 Parameters of dataset

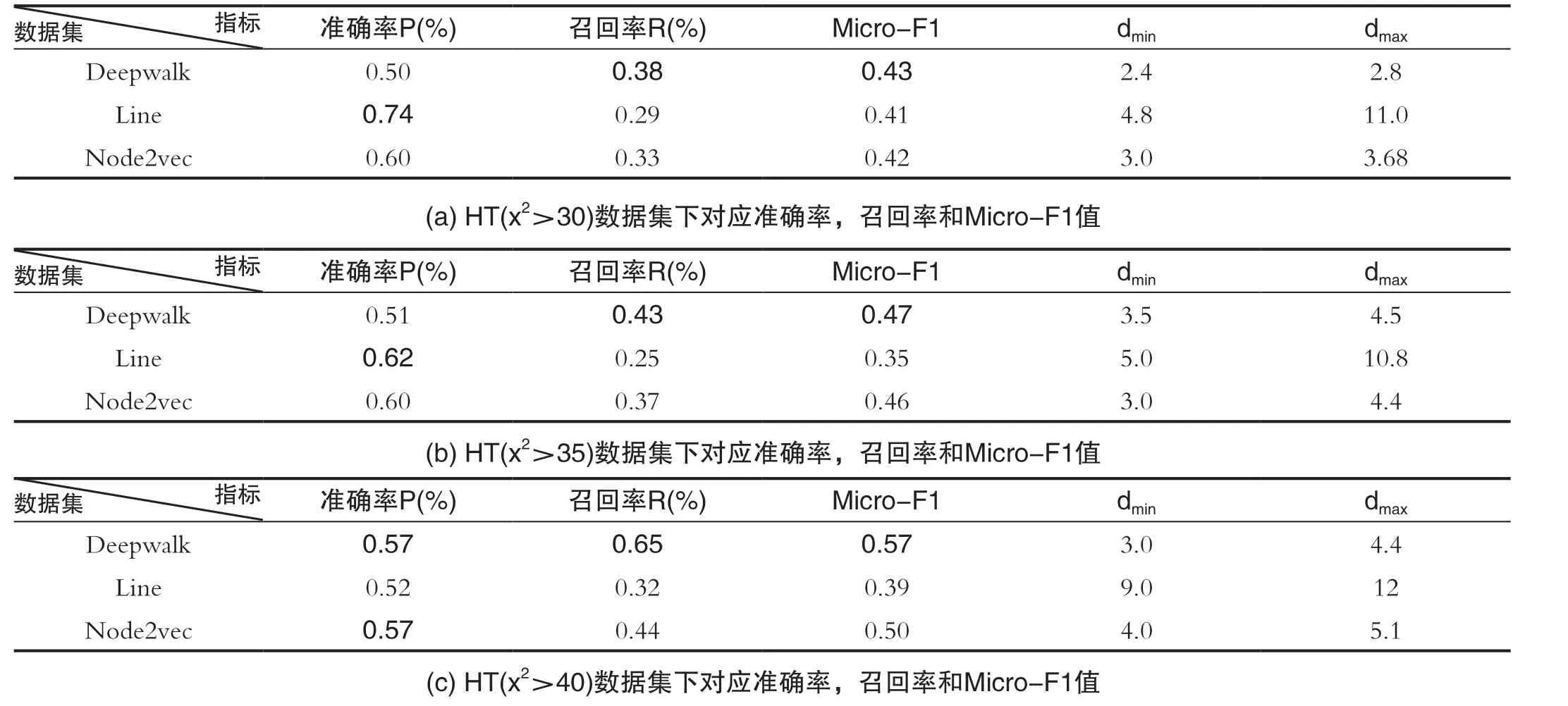
表 2 不同数据集下对应准确率，召回率和Micro-F1值Tab.2 Corresponding accuracy, recall and Micro-F1 values under different datasets

4 结语

本文旨在针对三种嵌入算法对复杂基因组网络预测性能的对比，以找出适合大规模基因组网络的嵌入算法。我们在三个不同高血压疾病交互网络上进行实验，得出DeepWalk在复杂基因组网络上取得更优效果的结论。

引用

[1] CUI P,WANG X,PEI J,et al.A Survey on Network Embedding[J].IEEE Transactions on Knowledge and Data Engineering,2018,31(5):833-852.

[2] ESTRIN D,GOVINDAN R,HEIDEMANN J.Embedding the Internet:Introduction[J].Communications of the ACM,2000,43(5):38-41.

[3] PEROZZI B,Al-Rfou R,SKIENA S.Deepwalk: Online Learning of Social Representations[C]//Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. 2014:701-710.

[4] TANG J,QU M,WANG M Z,et al.Line: Large-scale Information Network Embedding[C]//Proceedings of the 24th International Conference on World Wide Web,2015:1067-1077.

[5] GROVER A,LESKOVEC J.Node2Vec:Scalable Feature Learning for Networks[C]//Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.2016:855-864.

[6] CHOWDHURY G G.Introduction to Modern Information Retrieval [M].UK:Facet Publishing,2010.

[7] ADAMIC L A,ADAR E.Friends and Neighbors on the Web[J].Social Networks,2003,25(3):211-230.