含Ⅰ型中心裂纹板修补结构的应力强度因子计算

◎赵星 重庆交通大学航运与船舶工程学院

1.引言

船舶是海上运输的重要交通工具，其安全性受到了广泛重视。由于海洋环境的复杂多变性，船舶在波浪中航行时受载情况经常发生变化，这使船体结构长期处于交变应力状态，易于萌生疲劳裂纹。而严重影响船体结构安全的裂纹主要出现在船体甲板上，对于这种船舶甲板开裂情况，若不及时采取措施阻止裂纹的扩展，将会导致船体结构突然发生断裂，导致重大灾难事故的发生，2009年巴拿马籍油轮，2013年商船三井（MOL）号集装箱船的断裂就是因为疲劳裂纹的扩展导致的，为了保证船舶的安全运行，对裂纹损伤部位进行及时合理的修复是很有必要的。

现有一种碳纤维增强复合材料(Ca rbon Fiber Rein forced Polymer，简称CFRP)，具有重量轻强度高、抗疲劳和耐久性好、可设计性强等优点，已被广泛应用于飞机结构、混凝土、钢结构等的修复中，但总体上来说，主要集中在结构的加固、改造和补强中。

应力强度因子是表征外力作用下弹性物体裂纹尖端附近应力场强度的一个参量。在含裂纹结构进行强度评估中，不能仅使用常规的强度准则；断裂力学中提出了应力强度因子的概念，即裂纹端部应力强度由应力强度因子度量，能很好的评估裂纹结构的强度，因此在CFRP修复含裂纹结构中，要评估开裂结构的强度以及对裂纹的修复效果，需要计算裂纹尖端的应力强度因子，在裂纹板修补结构中的裂纹尖端应力强度因子有效的计算方法在此显得尤为重要。

2.国内外研究现状

对于复合材料修复结构应力强度因子的计算，在解析方法中，Erdogan等人考虑了胶层的弹塑性变形，采用复变函数方法分析了胶接修复结构的应力强度因子。Rose假设所有材料是线弹性，根据等效夹杂法推导出了修复结构应力强度因子的解析解。陈家权介绍了位移法的基本理论，并通过位移法理论计算公式求解了裂纹板裂纹尖端的应力强度因子说明了使用ANSYS计算应力强度因子的可用性；ROSE和Wang利用数值方法求解应力强度因子，以此为基础建立了关于应力减小修正因子的插值函数，能简洁有效计算应力强度因子。王海涛等人考虑裂纹长度变化的小尺寸裂纹建立了求解双边修补的裂纹应力强度因子求解公式。欧阳煜等人利用叠加原理导出了纤维增强复合材料(Fiber Reinforced Polymer，简称FRP)加固中心穿透裂纹板应力强度因子的解析表达式。穆志韬等人通过超奇异积分给出了应力强度因子的解法。

本文采取有限元模型计算和理论计算方法分别对矩形补片双面修补的含Ⅰ型裂纹板的裂纹尖端应力强度因子进行计算，由于各向同性板可以看成是特殊情况的各项异性板，本文对补片采用各向同性材料进行分析，且不考虑粘结层的脱粘。研究的模型参数为：裂纹板弹性模量为2.06E5MPa,泊松比为0.3，板长100mm,板宽32mm,，板厚为3mm；胶层弹性模量为2.9E3MPa,泊松比为0.3，胶层长60 mm，宽32mm,厚0.1mm；补片弹性模量为1.362E5MPa,泊松比为0.3，补片长60mm,宽32mm，厚1.5mm；模型单元采用SOLID185单元，裂纹半长分别取2～8mm进行计算。

3.ANSYS建模计算

采用ansys有限元软件对矩形补片双面修补裂纹板模型进行建模，由于裂纹板结构具有对称性，因此采用ansys APDL对模型板厚方向上半部分的1/2结构进行建模，就是整体模型的1/4，在Y坐标为0和Z坐标为0的对称面上施加对称边界，需要注意的是由于裂纹尖端具有奇异性，所以在裂纹尖端附近需要建立奇异网格，要使裂纹尖端临近节点向尖端节点移动1/4间距。

Ansys软件带有计算应力强度因子的功能，是采取位移法进行计算，位移法是通过提取裂纹尖端部分节点的位移进行计算，所以需要提取裂纹尖端附近节点的节点编号，定义裂纹路径，首先通过APDL语言快速建立好模型之后，便可以在软件后处理里面通过节点计算功能，定义裂纹路径，计算裂纹尖端应力强度因子，该功能也可以使用APDL语言实现，使用path命令定义路径，使用KCALC命令计算应力强度因子，取裂纹半长为8mm时的有限元模型进行展示如图1所示，通过对裂纹半长a分别为2～8mm的工况进行计算，得到计算结果如表1所示表所示。

图1 有限元模型

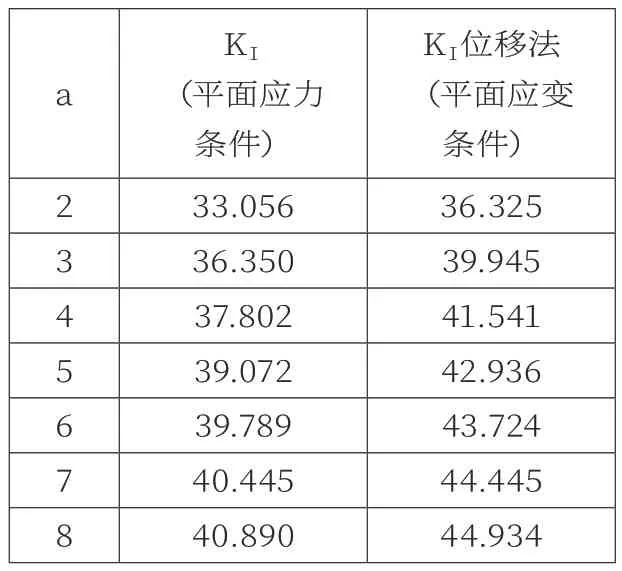
表1 ANSYS计算结果

4.位移法理论计算

该方法是通过提取裂纹附近的节点位移和坐标如图2所示，通过位移外推法求得参数A，之后带入计算公式（1）或（2）,计算裂纹尖端应力强度因子，裂纹尖端附近节点的位移可以通过建立限元模型计算完成之后进行：

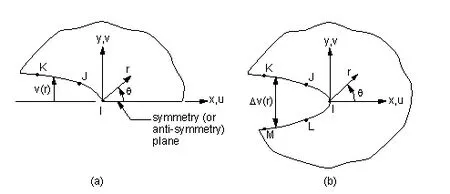
图2 提取裂纹尖端及附近位移的节点（a.半裂纹模型 b.全裂纹模型）

提取ANSYS模型计算得到的裂纹尖端节点位移信息带到位移法理论计算公式中进行计算得到计算结果如表2所示。

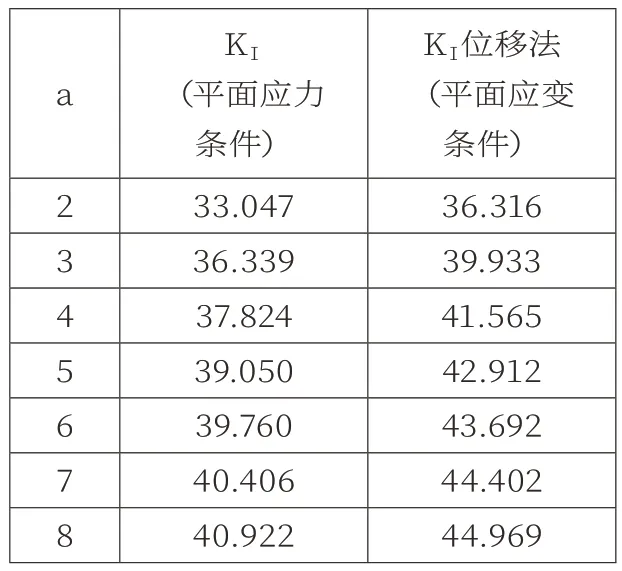
表2 位移法公式计算结果

5.ROSE计算解

根据ROSE计算修补之后的有限长度裂纹板应力强度因子的一般公式如公式（3）所示：

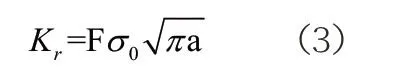
F 为修补后应力强度因子减小因子。

Rose根据其在文献[9]中提供的数值结果建立了插值函数F

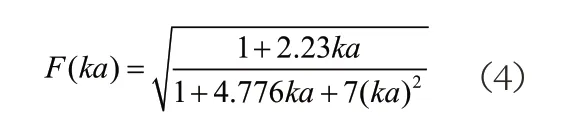
（4）式带入（3）式可得：

σ是未开裂裂纹板上应力

σ是裂纹板远端拉应力

B:补片宽度

A：补片长度

S：刚度比

针对Y 方向单向拉伸情况，λ取0。

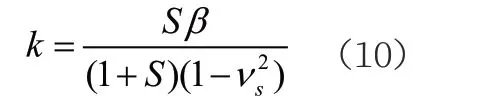
通过理论计算公式（3）得到应力强度因子如表3所示。

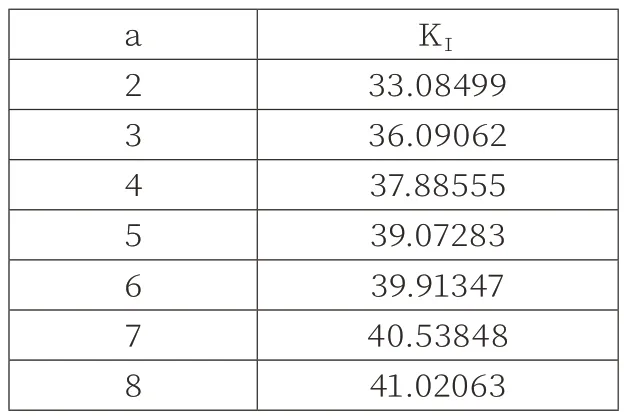
表3 Rose法计算结果

6.王海涛所引用方法

王海涛在文献中给出了CFRP矩形补片双面修补含中心Ⅰ型裂纹有限板的裂纹尖端应力强度因子计算公式为：

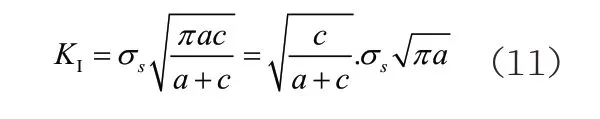
根据公式（11）计算裂纹尖端的应力强度因子得到计算结果见表4。

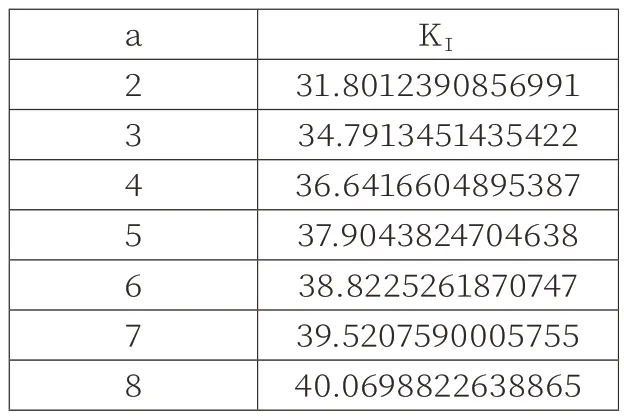
表4 王海涛所用公式计算结果

对位移法公式计算结果、ROSE计算公式、王海涛所用计算公式的计算结果与ANSYS建模分别在平面应力和平面应变条件下计算得到结果进行对比，与ANSYS在平面应力条件下计算结果对比如表5所示，与ANSYS在平面应变条件下计算结果对比如表6所示。

通过表5和表6可以得知ANSYS与位移法公式计算结果分别在平面应变和平面应力条件下的误差都很小，不超过1%；ANSYS在平面应变条件下的计算结果与ROSE计算公式、王海涛所用计算公式得到的结果对比，误差较大，均超过8%；ANSYS在平面应力条件下的结果与ROSE计算公式、王海涛所用计算公式得到的结果对比，误差较小，均在5%以内，其中王海涛所用计算公式得到的结果误差稍大一点，最大误差4.29%，ROSE计算公式得到的结果与有限元建模计算得到的结果误差均小于1%。

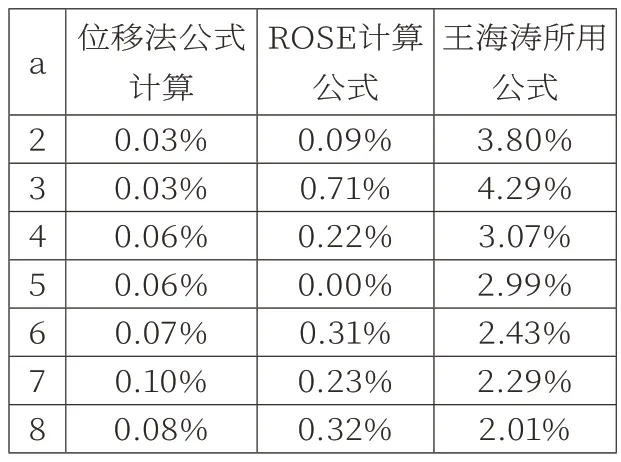
表5 平面应力条件下计算结果对比

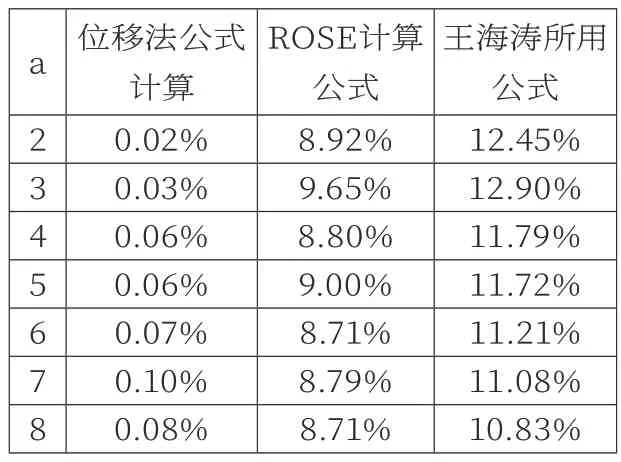
表6 平面应变条件下计算结果对比

7.结论

（1）文章采用的几种计算方法均可以得到较为一致的计算结果，王海涛所用计算公式精度相比于其他方法略低一点。

（2）ANSYS软件通过位移法计算解与位移法公式计算得到的应力强度因子误差很小，表明ANSYS采用位移法计算得到的应力强度因子解是有效的。

（3）ANSYS通过位移法计算得到的平面应力条件下的应力强度因子与ROSE计算公式、王海涛所用计算公式误差更小吻合度更高，因此采用平面应力条件下的计算结果较好。

（4）对中心裂纹板修补结构的应力强度因子求解，采用ANSYS建模计算的结果可靠性较好，可以采用该方法继续进一步研究补片参数变化对用力强度因子影响等问题。