基于FFRLS的电阻点焊预测模型
李 建,王 宾,梁立振,刘 伟
(1.安徽理工大学 电气与信息工程学院,安徽 淮南 232001;2.中国科学院 合肥物质科学研究院,安徽 合肥 230000;3.合肥综合性国家科学中心能源研究院(安徽省能源实验室),安徽 合肥 230000)
电阻点焊的原理是电流流过焊件产生的热量使点状区域熔化从而形成熔核来连接金属材料.电阻点焊技术应用广泛[1-2],由于其焊接过程极短,使用现场干扰颇多,导致焊接的过程具有非线性、耦合性、干扰性的特点,想要准确控制该过程变得困难.
在电阻点焊控制领域,目前已提出多种控制技术,其中应用最为广泛的就是工艺参数(电流、电压、功率)反馈控制,通过PID控制[3]、模糊控制[4]、神经网络[5]等控制策略对电阻点焊过程中的工艺参数进行反馈控制,以此来改善焊接质量.因为工艺参数反馈控制不涉及焊接质量信息,所以无法实现对焊接质量的闭环控制.针对该点不足,有学者提出了对能够反映焊接质量的本征信号进行实时反馈控制的电阻点焊自适应控制技术.在本征信号中,研究者们发现动态电阻和焊接过程联系紧密,更能够反映焊接材料在加热加压过程中焊件内部发生的动态特征变化[6].因此就有学者提出了使用模型预测控制策略跟踪动态电阻的方法[7],其中将电压与电阻的函数关系建立为预测模型,从而实现电阻的跟踪控制.但在实际焊接中动态电阻受多因素耦合影响而难以控制.
在Kas等[8]研究的热力学模型的基础上进行改进,提出的预测模型利用带遗忘因子的递推最小二乘法(FFRLS)对模型参数进行在线纠正,提高了模型的精确度.在本文中叙述了预测模型的推导,以及在MATLAB/Simulink平台上建立中频电阻点焊仿真模型,验证了预测模型的预测能力.
1 电阻点焊预测模型
预测模型包含两个部分,一部分是基于热力学平衡方程改进的预测方程,另一部分是在线参数估计.
1.1 预测方程
首先根据简化的点焊热力学方程[8]对焊接过程中的焊接电流与动态电阻以及温度变化之间的关系进行描述:
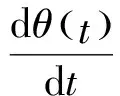
(1)
其中:dθ(t)为温升;I(t)为焊接过程中的电流;R(t)为焊接时的动态电阻;θ(t)为温度;a1、a2、a3为定值参数.此式即为简化的点焊热平衡方程,建立了温度与焊接过程变量I(t)与R(t)之间的函数关系.
在此方程上改进则需要引入电阻与温度之间的函数关系,将式(1)中与温度相关的量用动态电阻R(t)替换.将点焊过程中的动态电阻R(t)与温度之间的关系近似为:
R(t)=
R0[1+α(θ)(θ(t)-θ0)],
(2)
其中:α(θ)为电阻的温度系数;R0为室温下的电阻;θ(t)为当前温度;θ0为参考温度.变换形式可以得到:
θ(t)=φ(θ)(R(t)-R0)+θ0.
(3)
将式(3)对时间单位化有:

φ(θ)′(R(t)-R0),
其中
(5)

(6)
式(6)即为电阻点焊预测模型方程,式中Rk、Ik为当前采样时刻的焊接电阻和电流,可以通过采样检测得到.Rk+1则为被预测的变量,为下一采样时刻的动态电阻.参数ω0、ω1、ω2为与温度有关的时变参数,在具体应用时使用在线辨识的方法对其进行估算.
1.2 FFRLS参数估计
带遗忘因子的递推最小二乘方法(FFRLS)具有跟踪能力强、计算量小、收敛速度快的特点[9],并且可以抑制“数据饱和”现象,使得新数据影响变大[10],经常作为一种在线参数识别方法被广泛应用,本文将其应用在时变参数ω0、ω1、ω2的估算上.
利用FFRLS对预测方程的参数进行在线估计,首先将式(11)写成矩阵形式为:
(7)
再根据FFRLS的估算步骤:
(8)
(9)
(10)
式(8)—式(10)为FFRLS进行估算的迭代方程,其中Kn称为增益矩阵,Kn越大,修正效果越强.Pk为协方差矩阵,λ为遗忘因子(λ∈[0,1]).
在进行FFRLS迭代计算预测模型参数时,首先将ωk和Pk分别初始化为单位矩阵和单位矩阵的δ倍(δ∈(0,e-5));随后在每个采样时刻根据采集到的焊接过程信号进行迭代计算时变参数ωk;最后根据式(7)和计算得到的参数即可对下一采样时刻的动态电阻进行预测.
2 仿真与分析
2.1 仿真平台搭建
在仿真平台MATLAB/simulink中搭建图1所示中频电阻点焊系统验证本文方法的有效性.其中,负载Rx是利用lookup table 模块搭建电阻点焊动态电阻仿真模型,根据寰电智控科技公司生产的IDP-8210型号精密点焊机在低碳钢板上进行恒流焊接得到的动态电阻数据对真实的焊接动态电阻进行模拟,其中动态电阻随焊接时间变化的曲线如图2所示.

图1 中频电阻点焊仿真主电路

图2 电阻点焊焊接动态电阻曲线
预测模型在simulink中利用matlab fuction模块编写程序实现,输入当前采样时刻的电流和动态电阻,输出为预测的动态电阻.模型计算包括根据当前的焊接电流和动态电阻对预测模型的参数ωk进行计算,根据参数ωk对下一时刻的动态电阻Rk+1进行预测,实现预测模型的程序流程如图3所示.在仿真开始时需要初始化ωk、Pk、λ,其中ωk、Pk会以控制步长T为周期进行不断的迭代纠正,并且预测模型在每个控制步长都会输出一个预测的动态电阻,持续到仿真结束.

图3 预测模型程序流程图
2.2 结果分析
在搭建的仿真模型上进行恒流焊接控制仿真,观测到仿真焊接的过程中电流和电压波形如图4所示.在图中可以观察到电流在开始有一段上升过渡的过程,然后由于反馈的控制作用,电流稳定在设定值附近脉动,电压则在波形上跟随电阻变化呈现先上升后下降的趋势.该波形与实际焊接电流电压曲线吻合,证明该仿真模型具有较强的真实性.
为了验证预测模型的预测能力,将预测电阻和实际电阻进行对比,其结果如图5所示.其中(a)为预测模型输出的预测值和实际计算值之间的曲线对比图;(b)为误差率,误差率为预测值与实际值之间的偏差相较于实际值的比重.从图5(a)中可以直观地观察到预测电阻有一段快速上升跟上实际值的过渡过程,除此之外预测电阻与实际电阻两条曲线重合度很高,说明预测模型在收敛之后具备很高的预测能力.对比图4中的电流曲线,可以发现电流在达到设定值后,预测模型同步跟上实际值,证明电流上升过程对预测模型的过渡段存在影响.图5(b)中可以观察到预测模型在越过渡段后误差率逐渐减小并且稳定在0.03以内.由此可见,预测模型收敛后能够达到较高的预测水准.

图4 中频电阻点焊恒流控制仿真电流、电压波形图

(a)预测模型预测值与仿真实际值波形比较
3 结语
本文在电阻点焊的简化热平衡方程下,对电阻与温度之间的关系进行近似,进一步得到电阻点焊的预测模型,该模型可以在当前采样时刻利用采样数据进行计算,对下一时刻的焊接动态电阻进行估计.经过仿真实验,发现预测模型存在一段收敛的过程,证明该模型有较好的预测能力.对动态电阻的预测有利于焊接过程的自适应控制,针对该模型的改进和应用还需要进一步研究.

