自伴椭圆微分算子组广义谱的上界

黄振明

(苏州市职业大学 数理部，江苏 苏州 215104)

0 引言

微分算子的谱问题是数学和现代物理学中一类基本问题，具有广泛的应用性，一直受到众多学者的关注，但在一般的区域和边界条件下，根本无法求得精确的谱值或谱的显式公式，因此，多数情形下，人们只能依靠谱的定性理论估计其大致范围[1～6]，从而达到一定的实际应用。新近，笔者在文献[7]中探讨了如下定态薛定谔算子组的离散谱问题。

(1)

其中Ω⊂Rm(m≥2)是一个边界逐片光滑的有界区域，i=1,2,…,l，并得到了估计问题(1)第n+1个谱上界的一个解析不等式，但是，笔者发现，对问题(1)一般情形的高阶算子组问题讨论的中外文献并不多见，因此，本文将问题(1)中拉普拉斯算子的阶数推广至任意的正整数，考虑含不定权sij(x)的高阶自伴椭圆微分算子组的广义谱问题。

(2)

其中t≥1;l≥2皆为整数，i=1,2,…,l，n是Ω边界∂Ω的单位外法向量，aij=aji是正实数；νij(x)=νji(x)和sij(x)=sji(x)都是Ω→R上的非负函数(i,j=1,2,…,l)，且满足椭圆性等条件，即对任意向量ξ=(ξ1,ξ2,…,ξl)T，有

(3)

(4)

(5)

上述τi,μi(i=1,2)均为正实数。

1 准备知识

为方便推导，记l阶算子矩阵Rh(f)=fhEl×l，其中El×l为l阶单位矩阵，h为自然数，f为任一微分算子，l阶正定矩阵A=(aij)l×l，半正定矩阵V(x)=(νij(x))l×l，正定矩阵S(x)=(sij(x))l×l，l维函数列向量u=(y1，y2，…,yl)T,ui=(yi1，yi2，…,yil)T，将问题(2)化为矩阵形式：

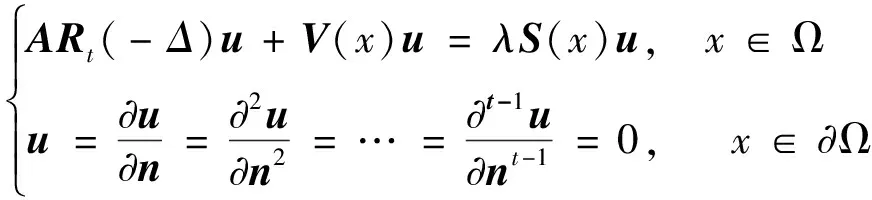
(6)

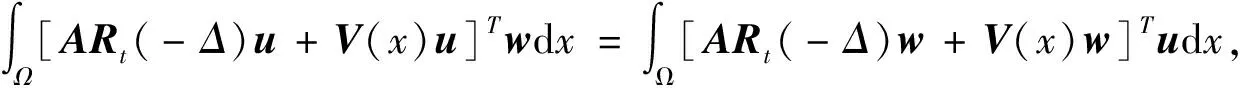
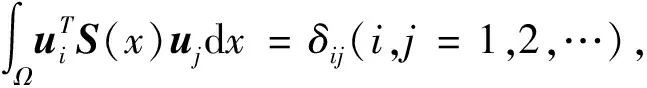
(7)

从问题(6)，利用特征向量的带权正交性、分部积分、式(3)和(4)，有

即

(8)

引入试验向量函数

(9)

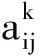
(10)

(11)

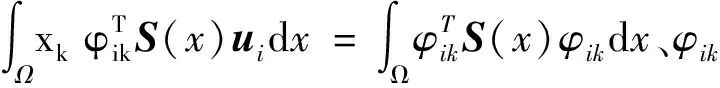
(12)

2 引理

引理1 设ui是问题(6)对应谱λi(i=1,2,…,n)的特征函数，则

证明 首先，用数学归纳法证明不等式

(13)

当p=1时，利用分部积分、Schwarz不等式和式(7)，有

此时式(13)成立。

假设p=k≤t-2时，式(13)成立，则当p=k+1时，类似地，利用分部积分、Schwarz不等式和假设条件，有

化简上式，得

即p=k+1时，式(13)也成立，于是式(13)得证。然后，反复利用不等式(13)和式(8)，得

引理1得证。

引理2 设ui是问题(6)对应谱λi(i=1,2,…,n)的特征函数，则

证明 a)利用分部积分和引理1，有

b)类似a)，分部积分，得

(14)

由式(14)移项得

(15)

利用式(3)、引理1和引理2(a)，从式(15)可得

引理2b)证毕。

证明 根据φik的定义，有

(16)

即

(17)

由式(16)、(17)和(7)得

(18)

利用式(18)、Schwartz不等式、(5)和引理2a)(其中取s=0)，有

(19)

根据式(19)，引理3得证。

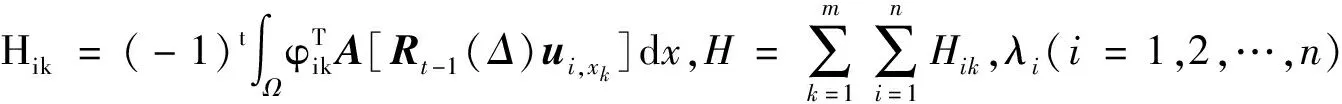
证明 将式(9)代入Hik可得

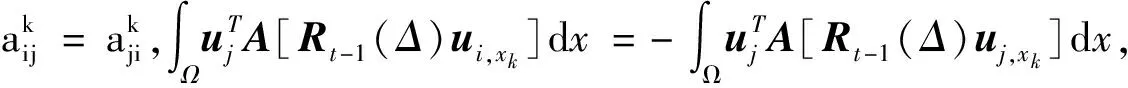
因此

最后，由引理2b)得

引理4得证。

3 主要结果

定理1 对于任意的整数m≥2,n≥1，自伴问题(6)的第n+1个谱有如下的显式估计①

(20)

证明 由式(12)可得

(21)

利用{λi}的单调递增性、式(10)和(21)有

(22)

式(22)即为

(λn+1-λn)W≤2tH

(23)

将引理3和引理4的估计结论同时代入式(23)，并用λn来替代其中所有的λi(i=1,2,…,n-1)，经化简即可得到式(20)。

注① 特别地，问题(6)当t=1且S(x)为数量矩阵，即S(x)=s(x)El×l时，恰好是参考文献[7]讨论的问题，此时，定理1中的式(20)就成为了文献[7]中的谱估计式(23)，且从式(20)知，在其它条件不变的情况下，随着空间维数的增大，λn+1与λn越靠越近。

定理2 对于任何空间维数m≥2，问题(6)的第n+1个离散谱有隐式估计②

证明 式(22)等价于

(24)

令式(24)中引入的参数σ>λn.利用式(18)、Young不等式和式(5)，得

(25)

根据引理1，式(25)右端第二项的上界可估计为

(26)

选取恰当的δ，使式(25)右端取得极小值，此时，由式(24)(25)和(26)可得

(27)

令不等式(27)右端等于零，简化后，有

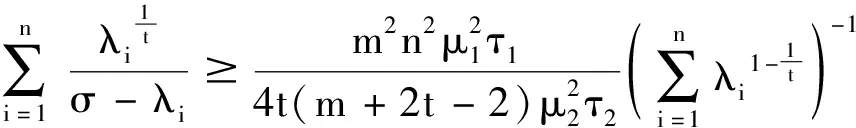
(28)

且从式(27)知，λn+1≤σ，于是用λn+1替代等式(28)中的σ，即得定理2.

注② 当问题(6)中t=1，且S(x)=s(x)El×l为数量矩阵时，定理2中的估计式恰好是文献[7]中的式(22)。

4 结语与建议

运用经典的Sturm-Lioullve定性理论，在薛定谔算子谱问题研究的基础上，进一步探讨了自伴椭圆微分算子组(6)的谱问题，得到了用前n个谱来估计第n+1个谱上界的两个万有不等式，在特殊情形下，本文的谱问题(6)恰好是参考文献[7]讨论过的问题，因此，所得结论包含了文献[7]中的两个谱估计不等式，在现代物理学尤其是量子力学中有着更广泛的参考价值，对于本文所论的自伴算子组在非齐次边界条件下的谱估计，也是今后值得深入思考的问题。