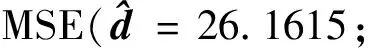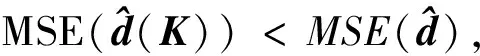混合系数线性模型参数的广义根方估计
蔡 齐,蔡择林,江秉华
(1.泰康保险集团股份有限公司稽核中心,湖北 武汉 430000;2.湖北师范大学 数学与统计学院,湖北 黄石 435002)
0 引言
考虑如下混合系数线性模型
z(t)=[x(t)]Ta+[y(t)]Tβ
(1)
其中x(t)=(x1(t),x2(t)…,xp(t))T,y(t)=(y1(t),y2(t),…,yq(t))T是t的已知向量函数,a是p×1的固定系数向量,β是q×1的随机系数向量,且β~(b,∑).
现对m个样品,分别在tij(ti1
测得以下数据:zij=[x(tij)]Ta+[y(tij)]Tβi+εij
(2)
这里的βi和εij分别是每个样品的随机系数和每次测量的误差,βi与εij独立,且
若记zi=(zi1,zi2,…,zini)T,εi=(εi1,εi2,…,εini)T
则可得:zi=Xia+Yiβi+εi
(3)

设Ci=(Xi,Yi),d=(aT,bT)T,ei=Yi(βi-b)+εi,则式(3)变为
(4)
进一步,记

z=Cd+e,e~(0,D)
(5)
这里还要求rank(Xi)=p,rank(Yi)=q,rank(Xi,Yi)=p+qg.
基于混合系数线性模型的广泛应用背景,许多学者研究了该模型的参数估计问题[3~11]。庄东辰等给出了d的LS估计[3],但当系数阵接近病态时,LS估计虽然无偏但均方误差过大。针对此情况,刘小茂等提出了一种有偏估计——根方估计[4],陈静进一步给出了局部根方估计[5]。本文拓广根方估计后,给出了广义根方估计,并证明了在均方误差意义下,广义根方估计分别优于上述估计,最后讨论了根方参数的选取问题。
1 广义根方估计
基于模型(5),庄东辰等给出了d的LS估计:
模型(5)的典则形式为:
z=Lr+e,e~(0,D)
其中L=CQ,r=QTd,QTCTCQ=Λ=diag(λ1,λ2,…,λg)
刘小茂等给出了d的根方估计:
(6)
其典则形式为:
其中0 若λ1≥…≥λh≥1>λh+1≥…≥λg,为改进根方估计, 陈静给出了d的如下局部根方估计: (7) 其中0 本文将根方估计(6)作如下拓广,将常数k用对角阵K代替,称 (8) 为d的广义根方估计, (9) 可以期望均方误差能够进一步下降。 式(8)的典则形式为: 为叙述方便,此处明确下文记号:若K=diag(k1,k2,…,kg) 证 显然 解得kj的最优值为: 定理得证。 即在均方误差意义下,广义根方估计优于根方估计。 从而 定理得证。 即在均方误差意义下,广义根方估计优于局部根方估计。 定理得证。 此处介绍极小化均方误差的无偏估计法, =rT(ΛK-I)2r+tr[(ΛK-I)2Λ-2LTML]+σ2tr[(ΛK-I)2Λ-1], σ2tr[(ΛK-I)2Λ-1] 模拟中,我们取p=q=1,m=1,n1=2.假设时刻tij服从[0,1]上的均匀分布,由MATLAB生成随机数t11=0.1270;t12=0.9058. 代入数据,由MATLAB计算得QTCTCQ=Λ=diag(2.4890,0.4944). 当0 k0.10.30.50.70.9MSE(^d(k))23.128717.698914.042912.132812.1885MSE(^dL(k))22.739117.208713.06419.96167.6419


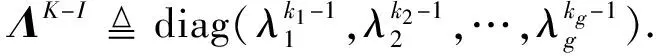
2 广义根方估计的性质


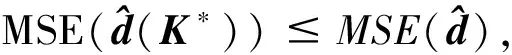



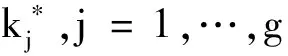

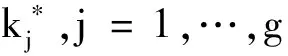

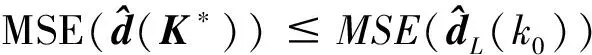
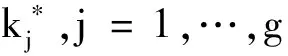
3 根方参数的选取
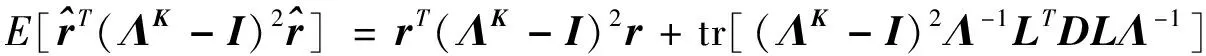

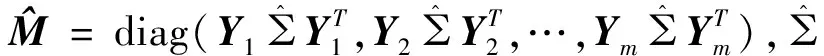
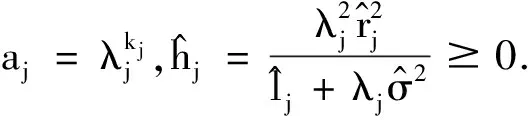
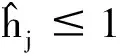


4 模拟算例