基于随机模拟探讨《中国药典》四分法取样的注意事项
寿纪纲,霍志鹏,王玉,何毅
(1.天士力医药集团股份有限公司研究院,创新中药关键技术国家重点实验室,天津 300410;2.中国药科大学 中药学院,江苏 南京 211198;3.天津中医药大学 中药学院,天津 301617;4.天津大学 药物科学与技术学院,天津 300072)
中药材和饮片由于自然或人为原因不可避免地在外观和成分含量方面存在差异,未必能保证批内或批间质量一致性,这给其抽样检测带来了较大困难[1-2]。而无论是在中药现代化研究中还是在药企的实际生产中,采用科学的抽样方法获得能够代表物料总体含量的样本,是决定后续过程的结果是否具有科学性和可靠性的前提条件。2020年11月4日,国家药监局药审中心发布了《中药均一化研究技术指导原则(试行)》,孙昱等[3]指出了获得均化物料必然包含的五个步骤,其中待均化物料的取样检测与均化效果确认两个步骤均涉及混合饮片的抽样评价,但目前尚无发现有明确提出可用于中药均一化的混合饮片抽样评价方法。
按照2020年版《中国药典》四部通则0211 药材与饮片取样法规定,供检验用药材或饮片的取样方法为四分法,其具体操作为:当从药材包件中抽取的样品总量超过检验用量的数倍时,可按四分法再取样,即将所有的样品摊成正方形,依对角线画“×”,使分成四等份,取用对角两份;再如上操作,反复数次,直至最后剩余量能满足供检验样品用量;最终抽取的供检验用样品量,一般不得少于检验所需用量的三倍即1/3 供实验室分析用,另1/3 供复核用,其余1/3 留样保存[4]。可以看到,四分法是一个逐步减小抽样样本量的过程,然而对于取样样本量大小与样本组成的变异却少见报道。
蒙特卡洛方法,也称统计模拟方法,于二十世纪四十年代被“曼哈顿计划”的成员John von Neumann 等人首先提出,是一种通过生成合适的随机数和观察一些服从特定性质或属性的数据来解决问题的方法,可通过计算机进行统计抽样试验来提供近似解[5-6]。因此本文依据蒙特卡洛方法对四分法的取样过程进行随机模拟,首先按照四分取样法的操作流程建立随机抽样模型,然后进行多轮模拟抽样并以抽样结果的频数分布代表抽样模型的概率基础,最后通过对抽样结果的频数分布情况进行对比与分析,探讨取样量与抽样结果变异大小的关系。
1 材料与仪器
Windows 10 系统计算机(处理器:Core i7-855U四核1.8 GHz,内存:8G);Python3.8;GraphPad Prism7。
白芍饮片(天津天士力现代中药资源有限公司,2007002);焦糖色(上海爱普食品工业有限公司)。
2 方法与结果
2.1 混合饮片抽样模型的建立
取同一批白芍饮片1 800 g,其中900 g 用焦糖色染成黑色,代表一批白芍饮片,剩余900 g 代表另一批白芍饮片,将两批饮片充分混合后作为抽样总体,混合效果如图1所示。抽样样本的大小依照《中国药典》一部白芍饮片项下的【鉴别】、【检查】、【含量测定】、【浸出物】设置为30 g。基于抽样总体的平均片重(0.25 g/片)可以将实际抽样过程转化为从7 200 片随机混合的饮片总体中抽120 片的过程。饮片取样模型采用编程软件Python 3.8 建立,建模流程如图2所示。

图1 染色白芍饮片与未染色白芍饮片混合效果图Fig.1 Mixed effect of dyed and non-dyed pieces of Radix Paeoniae Alba

图2 混合饮片抽样模型运行流程图Fig.2 Operation process of sampling model of mixed decoction pieces
将实际抽样与模拟抽样各100 次的结果的频数分布情况进行对比,如图3a所示。从图中可以看到两条曲线的形状近似且均在未染色饮片占比为0.5 时累计频数达到最大,这说明将混合饮片抽象化为均匀的抽样单位后使用计算机进行模拟抽样可以对实际抽样的情况进行初步预测。
从抽样结果的产生的过程分析,上述抽样服从二项分布规律,基于二项分布的理论概率对此进行验证[7]。将混合饮片抽样模型的抽样次数设为100 000,得到抽样模拟的结果后使用GraphPad Prism 软件分别对模拟抽样结果和基于二项分布理论概率预测的结果绘制频数分布曲线如图3b所示。可以看到两条频数分布趋势线基本一致,这说明对于两批饮片混合得到的抽样总体,当抽样总体量与抽样量相差较大时,抽样过程符合二项分布的抽样模型。

图3 实际抽样与模拟抽样各100 次的结果的频数分布情况进行对比Fig.3 Comparison of frequency distribution between actual sampling and simulated sampling
2.2 基于随机模拟探讨“四分过程”对抽样结果的影响
基于随机模拟探讨《中国药典》0211 药材与饮片抽样法中的“将所有的样品摊成正方形,依对角线画“×”,使分成四等份,取用对角两份”过程对抽样结果的影响。使用Python 3.8 编程语言分别建立四分过程抽样模型与直接随机抽样模型。
建立四分过程抽样模型思路如下:使用random库中的随机数函数生成一个长度为900 的数组并使每一个数代表染色饮片与未染色饮片的概率各为1/2,表示从两种饮片1∶1 混合的无限大的抽样总体中获得一个包含900 个饮片的抽样大样本;同时将获得的抽样大样本排列为30×30 的正方形平面并使用matplotlib 库绘图表示;然后从“正方形”的对角线处将平面分为四个区域且使每个区域内的饮片数相等;最后将“正方形”上下两个对角区域的饮片合并作为模拟四分过程抽样的结果,建模流程如图4所示。

图4 四分过程抽样模型运行流程图Fig.4 Operation process of quartering process sampling model
直接随机抽样模型按照相同方式获得抽样大样本,但将四分过程取消,而是直接随机从抽样大样本中取出半数饮片作为抽样结果。
将两个抽样模型的抽样次数均设为100 000,得到抽样模拟的结果后使用GraphPad Prism 软件分别对它们绘制频数分布曲线,如图5a所示;运行四分过程抽样模型后可同时得到四分过程绘图的结果如图5b所示。黑色圆点表示染色饮片,白色圆点代表未染色饮片;按照四分过程的步骤,从对角线处将“正方形”分为四个区域并保证每个区域中的饮片数相等,如图5c所示。对照图5c 中的白色区域,从图5b 中取出对应位置的饮片作为四分过程的抽样结 果。
从图5a 中可以看到两条频数分布趋势线基本一致,这说明当抽样总体是随机分布时,使用包含四分过程的取样方法进行抽样与直接随机抽样产生的结果是一致的。

图5 抽样模型软件模拟图Fig.5 Sampling model software simulation diagram
2.3 基于随机模拟探讨重复抽样过程对抽样结果的影响
基于随机模拟探讨《中国药典》0211 药材与饮片抽样法中的“如上操作(四分过程),反复数次,直至最后剩余量能满足供检验用样品量”过程对抽样结果的影响。
重复过程抽样模型采用编程软件Python 3.8 建立,使前一次抽样得到的样本作为下一次抽样的抽样总体并继续按照相同的抽样过程进行下一次抽样,直至获得最终样本,建模流程如图6所示。

图6 重复过程抽样模型运行流程图Fig.6 Operation process of repeated sampling process sampling model
重复抽样过程是一个逐步减小样本量的过程,为探究逐步减少抽样样本的过程对抽样结果的影响,对重复抽样四次过程中初始样本到最终样本的均值变化情况进行分析。将重复过程抽样模型的初始大样本量设置为5 760,抽样次数设为100 000,循化抽样数依次设为1、2、3、4、5,即对包含5 760 个抽样单位的抽样大样本进行反复抽样分别获得最终样本量为2 880、1 440、720、360、180 的抽样结果并绘制频数分布曲线,如图7所示;然后分别对上述抽样结果落于期望值±5%区间内的累计频数进行统计,如表1所示。可以看到随着抽样样本量减小,模拟抽样结果的频数分布区间逐渐增大;而抽样结果落入期望值左右固定区间内的累计频数逐渐减小。
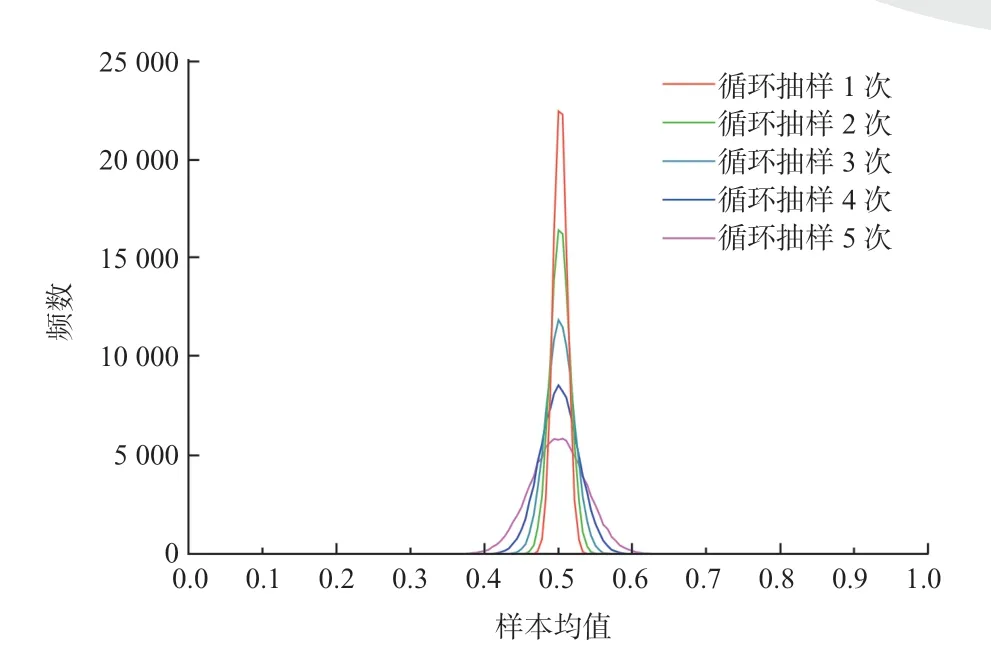
图7 对包含5 760 个饮片的抽样大样本循环抽样1 次、2次、3 次、4 次、5 次的抽样结果对比Fig.7 The sampling results of one,two,three,four and five times of cyclic sampling for large sample of 5 760 decoction pieces
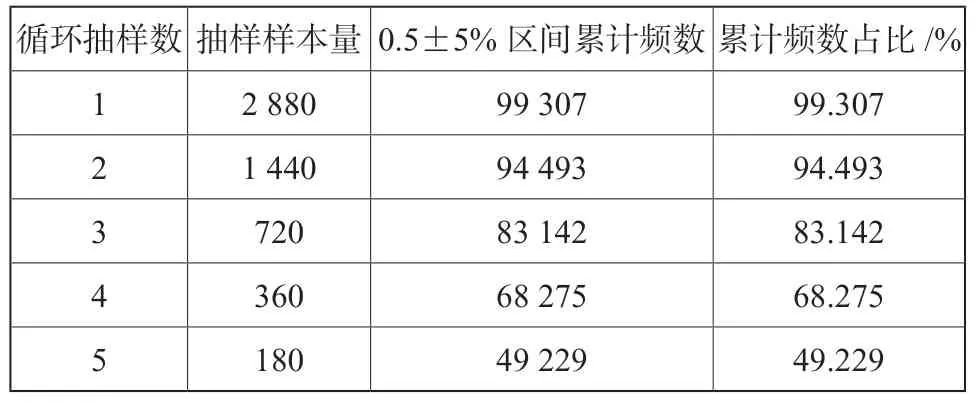
表1 对包含5 760 个饮片的抽样大样本循环抽样不同次数时抽样结果落于0.5±5%区间的累计频数及其占比Tab.1 The cumulative frequency and proportion of the sampling results of 5 760 decoction pieces in the 0.5±5% with different times of cyclic sampling
对循环抽样数不同时抽样结果的变异进行考察,分别以2 次、3 次、4 次、5 次、6 次、10 次抽样作为一轮并计算每轮结果的相对标准偏差(RSD),通过计算机模拟得到10 000 轮抽样模拟的RSD 并对其小于5%的轮数占比进行统计,如表2所示。可以看到在每轮抽样次数不同时,10 000 抽样模拟的RSD 小于5%的比例都会随抽样样本量减小而减小,以5 次抽样作为一轮为例,对循环抽样数不同时10 000 轮抽样模拟的RSD 的频数分布情况进行作图,如图8a~e所示;当循环抽样数不同时,随每轮抽样次数的增加,10 000 轮抽样模拟的RSD小于5%的比例的变化规律不一致,分别对循环抽样数为3、4、5 时,抽样模拟的RSD 在每轮抽样次数不同时的分布情况进行作图,如图8f~h所示。此外根据二项分布的数学模型可以推导得到抽样量一定时理论RSD 的计算公式为RSD=σ(x)/μ(x)=[7],计算得循环抽样数为3、4、5时理论RSD 分别为3.726%、5.270%、7.453%,并将它们标注到图8(f~h)中,可以看到在循环抽样数一定时,随每轮抽样次数的增加,RSD 分布的拟合曲线近似为钟形且分布范围逐渐减小,其对称轴逐渐趋近于理论RSD。
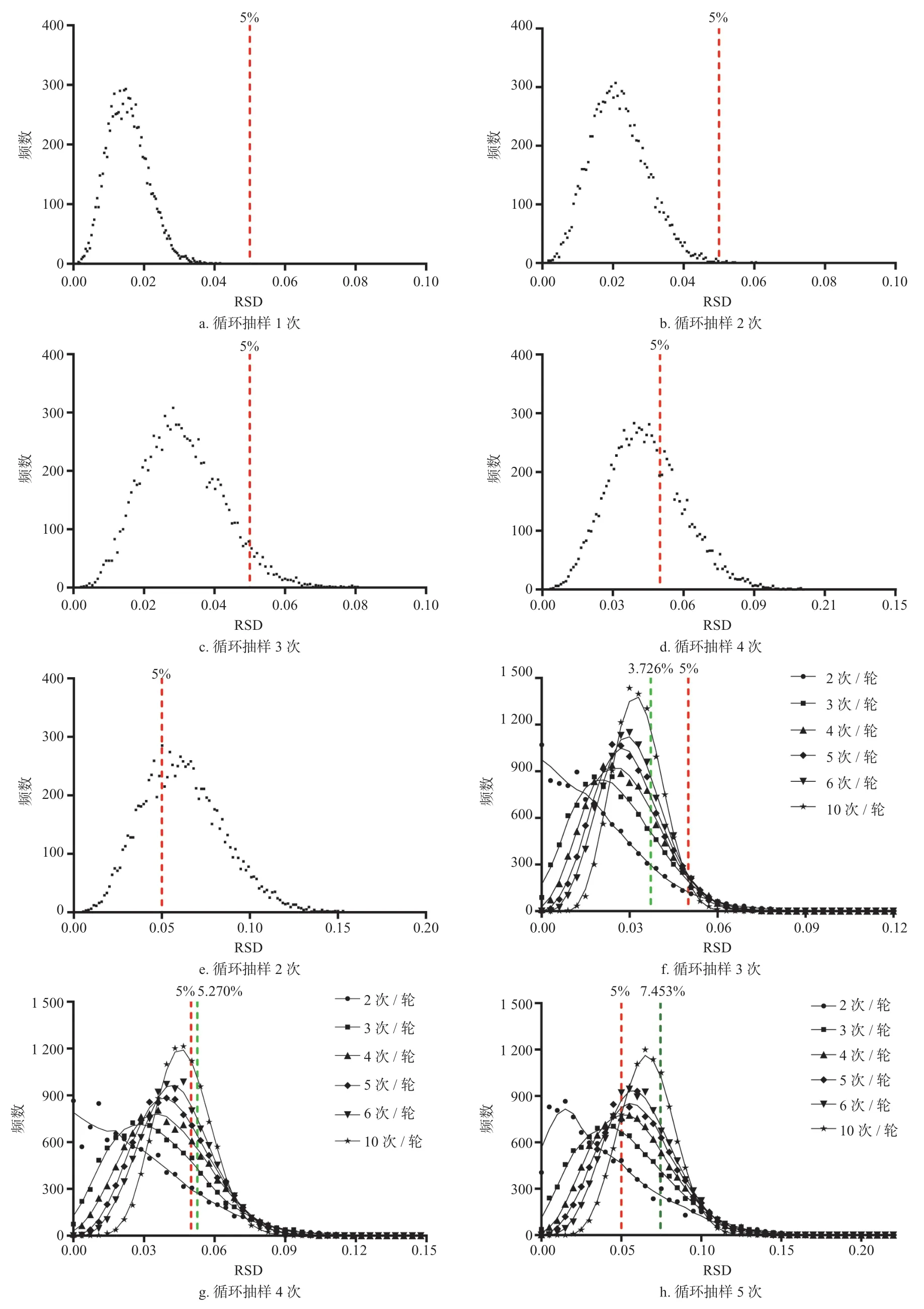
图8 抽样模拟的RSD 分布情况Fig.8 RSD distribution of sampling simulation

表2 每轮抽样不同次数且不同循环抽样数时10 000 轮抽样模拟的RSD 小于5%的占比Tab.2 When the number of cyclic sampling and sampling number of each round is different,the proportion of RSD simulated by 10 000 rounds of sampling that is less than 5%
最后对重复抽样方式与直接随机抽样方式进行对比。将2.2 中直接随机抽样模型的抽样大样本数与抽样样本数分别设置为5 760 与180,使之能够通过一次抽样从抽样大样本中直接获得最终样本;然后将重复抽样模型与直接随机抽样模型的抽样次数均设为100 000,得到它们抽样模拟的结果后使用GraphPad Prism 软件绘制频数分布曲线,如图9所示。从图中可以看到两条频数分布趋势线基本一致。这说明当抽样总体是随机分布且最终样本量一定时,使用重复抽样与直接随机抽样产生的结果是一致的。

图9 重复过程模拟抽样与直接随机模拟抽样的结果对比Fig.9 Comparison between results of repeated process simulation sampling and direct random simulation sampling
3 结论
本文按照《中国药典》通则中的饮片取样方法四分法的操作步骤使用计算机语言Python 建立了混合饮片的抽样模型,然后基于蒙特卡罗方法得到了四分法模拟抽样结果的概率分布情况,并对其进行了分析,旨在探讨四分法的抽样方式与抽样量对抽样结果代表性以及变异性的影响。相对于繁重的人工取样统计,计算机模拟混合饮片取样可在短时间内获得大量模拟数据,有助于快速了解抽样的概率分布特征[8]。
由模拟结果分析发现,当抽样总体是随机分布且最终样本量一定时,计算机模拟四分法抽样与模拟直接随机抽样产生的结果是一致的,且四分法抽样结果的代表性同样会由于样本量的减小而降低[9]。实际上,随机分布状态是一种完全混合状态[10],当物料未达到完全混合的状态时,由于四分取样法包含对中间样本重新混合的过程,可能对减少抽样变异有一定改善效果;在已经充分混合的总体中,为使抽样样本具有充分的代表性,需要根据抽样的具体情况评估合理的抽样量大小。
考虑到变异性也是反映抽样代表性的指标之一[11],针对不同抽样量时抽样结果的RSD 分析,发现当抽样样本量减小时,样本的RSD 增加,每轮抽样模拟RSD 小于5%的概率会减小;当每轮抽样次数增加时,RSD 的分布范围逐渐变小且其对称轴逐渐趋近于理论RSD,这提示设计适当的抽样次数才能获得接近理论分布的RSD。以循环抽样数为5 时为例,两次抽样作为一轮时,模拟抽样的RSD 落在理论RSD 周围的概率远小于10 次抽样作为一轮时,且两次抽样结果的均值实质上有更大的变异,此时以2次抽样的RSD 评价抽样代表性显然是不合理的。
由于中药原料来源的复杂性,很多情况下无法得知混合饮片的具体情况,很难综合判断抽样方法本身对抽样结果产生的影响,从影响混合的主要因素入手对抽样过程进行简化或为一种可行的解决方法[12]。本研究发现实际抽样与模拟抽样的结果频数分布曲线相似度较高,这表明随机因素为影响物料混合的主要因素,因此本文从随机混合的角度入手,对抽样方式与抽样量对抽样结果代表性以及变异性的影响进行了初步推测,有助于为中药均一化发展中更合理的混合饮片抽样评价方法提供参考。

