基于连续小波变换的房价与股价因果及联动关系

王敏会，尹晓翠，刘伟，张艺琳

(1.青岛农业大学理学与信息科学学院，山东青岛 266109；2.青岛农业大学经济管理学院；3.青岛农业大学巴瑟斯未来农业科技学院)

研究经济序列之间的联动和因果关系，现有文献大多分为三类：①传统方法，包括Granger因果关系检验、协整分析、误差修正模型等[1-3]，分析序列之间静态的时域关系；②动态方法，包括状态空间模型、拔靴分样本滚动窗口因果关系等[4-5]，分析序列之间关系的时变性质或结构变化；③频率方法，包括傅里叶方法[6]，分析不同频率下序列间的关系。这些方法通常只考虑了时间或频率的单一角度。小波分析方法通过时频变化突出序列在某些方面的特征[7]，是傅里叶分析的良好替代。虽然傅里叶分析可以借助谱技术揭示不同频率下序列间的关系如何变化，但它丢弃了局部时间上的信息[8]。另外，傅里叶分析只适用于平稳序列。相比之下，小波分析估计时间序列的光谱特征作为时间的函数[6]，可以同时提取时域和频域的局部信息。此外，小波分析比傅里叶分析具有显著的优势，它可以适应非平稳或局部平稳序列[9]。小波分析能够进行多分辨率的时频域分析，特别适合非平稳序列，近些年来，越来越多地被应用到经济领域，以分析经济序列及其相关性。

本文采用小波分析方法，探讨了股价和房价在时域和频域之间的联动和因果关系。小波分析将潜在的时间序列扩展到时频空间，可以以直观的方式呈现序列的时变和频变信息。小波相干性和相位差同时评估了股价和房价之间的联动及因果关系如何在时间-频率窗口内随时间及频率变化。通过这种方式，可以观察到两个市场之间的高频(短周期)和低频(长周期)关系，以及可能的结构变化和时间变化。本文提供了一个研究股票和房地产市场关系的合适工具，为该领域的研究提供新的视角。

1 理论方法

母小波ψ(t)通过简单的伸缩和平移可以得到子小波族：

(1)

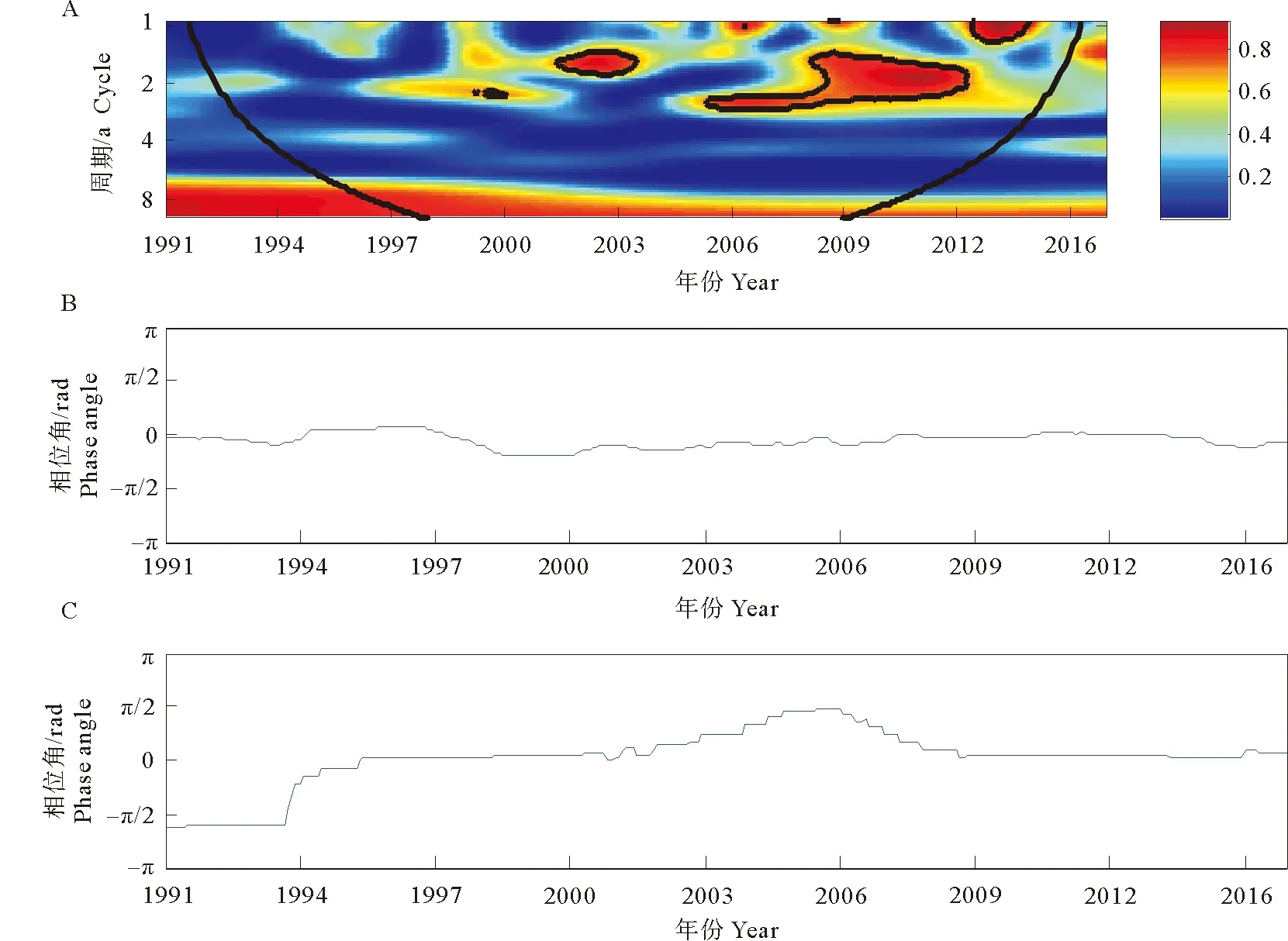
其中a是控制小波位置的平移参数，b是控制小波宽度缩放或扩张的尺度参数，t代表时间。

给定离散时间序列，其连续小波变换为：

(2)

其中ψ*(t)为ψ(t)的复共轭函数。小波在时域上的位置由a给出，在频域上的位置由b给出。小波变换将原始序列映射为a和b的函数，同时得到时间和频率的信息。相关文献建议了几种具有不同性质的母小波ψ(t)，而Morlet小波因其易解读性而获得广泛的应用。Morlet小波的形式为：

(3)

其中π为圆周率，e为无理数，ω0表示频率，应用中常取ω0=6。

小波能量谱被定义为：

|(WPS)x(a,b)|=|Wx(a,b)|2

(4)

它测度时间序列在时间和频率域内的方差，高的小波能量谱反映序列的高波动性。

实际应用中，通常需要量化两个时间序列的关系。交叉小波能量谱、小波相干性和小波相位差能够处理两个时间序列的时频依赖关系。两个时间序列x(t)和y(t)的交叉小波变换定义为：

(5)

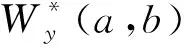
(6)

两个时间序列的交叉小波能量谱描述它们在每个时间和频率上局部协方差的大小。

为了分析两个序列的关系，引入小波相干性来测度时间和频率域上的相关性。小波相干性数值介于0和1之间，且越接近于1，两个序列的相关性越大，反之越小。两个序列的小波相干性定义为：

(7)

其中S表示时间和尺度上的平滑算子。

虽然小波相干性可以提供两个序列相关性强弱的测度，但无法区分序列间的正负相关性。为了区分在时间和频率域内序列的正负相关性及其领先-滞后关系，引入相位角。当小波ψ(t)是复值时，小波变换Wx(a,b)也是复值，可分为实部R{Wx(a,b)}和虚部S{Wx(a,b)}，则小波相位角定义为:

(8)

相位角为0意味着两个序列一起联动，相位角为π(-π)意味着两个序列完全反向运动。如果ωxy∈(0,π/2)，则两个序列正相关，且x(t)领先于y(t)；如果ωxy∈(π/2,π)，则两个序列负相关，且y(t)领先于x(t)；如果ωxy∈(-π,-π/2)，则两个序列负相关，且x(t)领先于y(t)；如果ωxy∈(-π/2,0)，则两个序列正相关，且y(t)领先于x(t)。

2 实证分析

房价与股价的关系与互动机制一直是学术界关注的重点，两者之间的关系可以通过两种传导机制来解释。“财富效应”表明，股价上升所产生的额外收益可以提高房屋的消费和价格；“信贷价格效应”表明，房价上升可以提高抵押品的价值并减少企业和家庭的借贷成本，因此能够刺激经济活动并提高企业未来盈利，从而影响股价。本文从RESSET数据库[10]调用了1991年1月至2016年9月期间全国房屋销售价格和上证综合指数收盘价的月度数据，其中房屋销售价格数据是根据所查的商品房销售面积和销售额计算得到的平均销售价格。对数据取对数处理以消除异方差的影响，然后利用Matlab软件处理得到小波分析的结果。图1和图2分别给出了房价和股价的小波能量谱图。小波能量谱图中：纵轴表示周期，用颜色标记序列的波动性大小，高能量(高波动性)和低能量(低波动性)分别用红色和蓝色来表示。小波能量谱图中，粗黑线表示由蒙特卡洛法模拟2 000次得到5%显著性水平下的估计值。使用周期代表频率，1～2 a代表短周期，2～4 a代表中周期，4～8 a代表长周期。

从图1房价的小波能量谱图中可以看出，1994—1997年间，房价在1～2 a的短周期内具有明显的波动性。20世纪90年代，随着我国住房改革的逐步推进，房地产市场发展出现了以沿海城市为中心的第一轮高潮，政府从1993年开始实行房地产紧缩调控以抑制市场过热。房价在1993年前持续上升到最高点，之后迅速下降，到1994年达到最低点，之后在1997年由于亚洲金融危机的影响又迅速下滑，因此在这段时间内表现出明显的波动性。

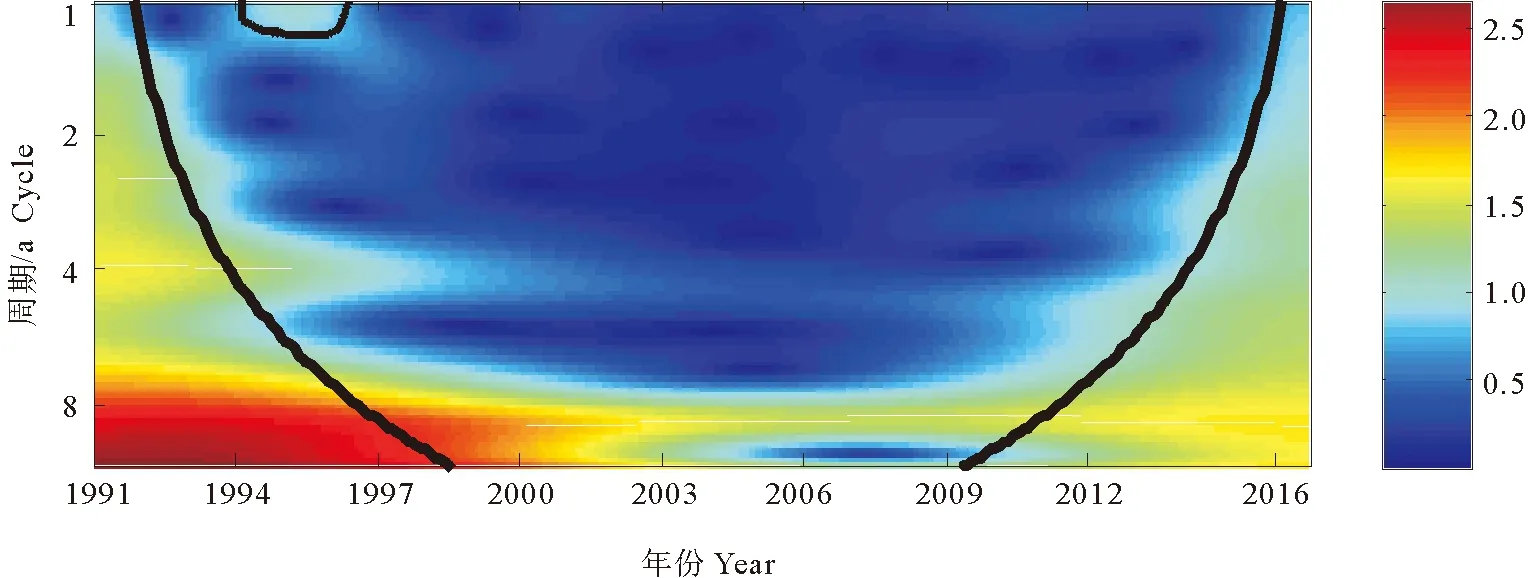
图1 房价的小波能量谱

从图2股价的小波能量谱图中可以看出，整体上股价在1～2 a的短周期内波动性不显著，在2～4 a的中周期内具有一定的波动性，在4～8 a的长周期内，股价均具有较强的波动性，这与我国股市多年来一直处于大起大落的震荡状态是相符的。值得注意的是，股价在2008年前后具有显著的波动性，这是因为，该时期上证综合指数正处于牛熊市轮替阶段，并受国际金融危机影响，上证综合指数在不到1 a的时间内从2 675点升至6 124点，随后又在短短1 a的时间内跌至1 664点，造成股价的剧烈波动。

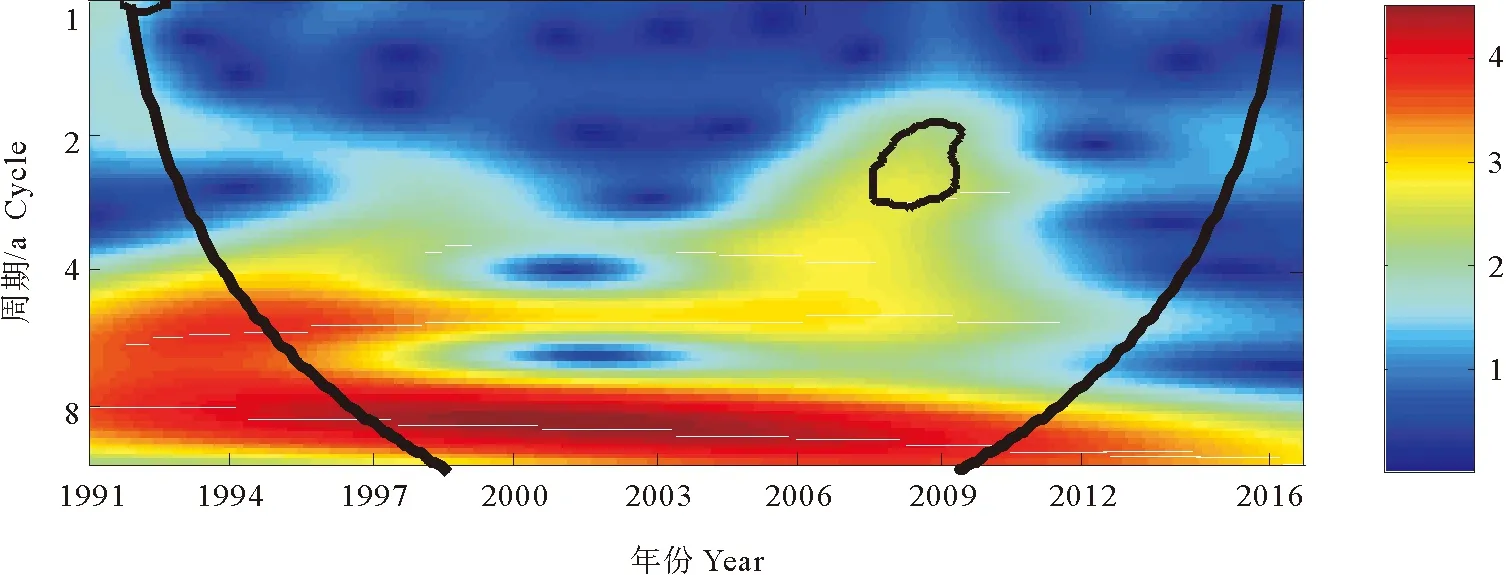
图2 股价的小波能量谱

小波相干性可以进行三维分析，即可以同时考察时间、频率和关联强度3个因素，而相位角可以用来考察两个序列的领先-滞后关系。小波相干性和小波相位角图中红色代表强相关，蓝色代表弱相关。从图3可以看出，我国房价和股价的关系随时间和频率变化，表现出变化的不稳定性关系，且在这段样本期内，大部分时间存在正向相关关系(相位角位于第一或第四象限)。在2002—2004年间，1～2 a短周期内，房价和股价具有显著的短期正相关性，并且这段时期内，股价显著影响房价。2001年后，我国股票市场转入熊市，股价震荡下跌，股民财富缩水，从而减少了对房地产市场的投资，对房价也产生明显的影响，股价变化带来的财富效应明显。

A. 小波相干性； B. 1～4 a频率段相位角；C. 4～8 a频率段相位角。

2005—2012年这段时期，1～4 a中短周期内，房价和股价具有显著的正相关性，且相位角接近于0，表明房价和股价二者的变化具有明显的同步性。受全球经济危机影响，2008年，我国房价和股价都出现明显下滑，之后政府实施一系列积极的政策，使房价和股价在2009年迅速回升，这段时期表现出较强的同步性。此外，在2013—2014年间，1～2 a的短周期内，房价和股价同样表现出明显的正相关性，并且也具有明显的同步性。从4～8 a的长周期看，房价和股价的相关性较强，但不显著，且由于1996年之后，相位角位于第一象限，长周期内房价影响股价更多，表明长周期内房价上涨对股价产生正向影响，股价的波动对房价波动的影响则十分微弱，这与沈悦等[11]的研究结果是一致的。由于我国股市的不稳定性，投资者在长期投资方面更青睐于房地产市场，因此从长周期来看，股价变化带来的财富效应对房价影响较小，而房价变化带来的信贷价格效应对股价影响较大。

3 结论

本文利用连续小波变换方法研究我国房价和股价之间的联动和因果关系，以及两个序列随时间和频率变化的动态关系。研究发现，从中短周期来看，2002年之后，我国房价和股价表现出明显的同步性；而从长周期来看，房价影响股价更多，房价上涨对股价形成显著的正向影响，而股价的波动对房价影响则十分微弱。