基于12成分模型和分子动力学的沥青材料性质模拟研究

郑仕跃，邹卓民，周权峰，朱应

(1.中海建筑有限公司，广东 深圳518057；2.中南大学 土木工程学院，湖南 长沙410075；3.比利时鲁汶大学 建筑工程学院，比利时 根特9000)

沥青是一种高度复杂的材料，主要来源于原油蒸馏的副产品，被广泛用作道路路面的黏结剂。沥青包括数百万不同的有机分子，这些有机分子的极性和分子量差异很大[1]。因此，沥青的物理、化学和力学性质在一定程度上取决于极性和非极性分子的含量以及大分子和小分子之间的比例[2]。几十年来沥青这种材料一直在被使用和研究，但其结构组成和性能仍然存在不确定性[3-5]。沥青的化学成分和分子结构影响着沥青的物理性能和力学性能，从而直接影响沥青路用性能[6-7]。研究人员通过物理分离方法(在活性氧化铝上进行选择性吸附−解吸附)研究沥青的成分，得出沥青材料由3种主要成分组成，即沥青质，数值和油分[8]。此外，美国试验与材料学会(ASTM)提出了4组分概念，将沥青分为饱和组分、芳香组分、树脂组分和沥青质组分[9]。目前，许多研究人员基于以上分类方法利用分子模拟技术，将沥青各组分的分子结构和相互作用与宏观物理，化学和力学性质联系起来[10]。唐伯明等[11]采用分子动力学模拟方法，基于自由体积理论开展了沥青分子模型黏度预测研究。YANG等[12]采用分子动力学方法研究了时间为皮秒级沥青的氧化老化行为。SONIBARE等[13]采用分子动力学方法对废弃植物油中主要脂肪酸成分及其与模型沥青混合料在不同温度下进行了分子动力学模拟。LUO等[14]采用分子动力学模拟方法研究了沥青氧化老化对沥青混合料热力学性能和界面结合性能的影响。基于传统的4组分模型，LI等[15]提出了一种新的沥青分子组成(12成分模型)，它能更好地表征沥青的物理和力学性能，但由于键的冲突产生的戊烷效应，使得该沥青质分子具有较高的内能。因此，LI等[16]改变了烷基的位置，降低了分子内部的高内能。虽然有一系列关于沥青材料分子动力学的研究成果，但针对沥青材料的各种物理性质(密度、黏度、表面自由能和内聚能密度等)采用3组分还是4组分的分子模型计算更适用的问题还少有研究。鉴于12成分的沥青分子模型能更好地表征沥青的基本性质，本文基于12成分的沥青分子模型，展开沥青基本性质的分子动力学研究。首先，基于CVFF力场以及LAMMPS分子模拟软件，建立2种沥青分子模型(3组分沥青分子模型和4组分12成分沥青分子模型)。然后，利用分子动力学模拟方法分别计算2种沥青分子的物理力学性质(密度，黏度和能量密度)，同时与其他研究人员试验结果和模拟结果相对比，验证本文的模型和方法。

1 分子动力学模型的建立与模拟

1.1 沥青分子模型建立

首先，将所有类型的分子放置在初始密度为0.1 g/cm3的周期性盒子中，防止分子链相互扭曲，建立分子随机分布的沥青模型，分子组成与分子式如表1和表2以及图1和图2所示。采用Nose-Hoover热浴法将模型升温至533.15 K，并在NVT系综(等温等容系综)下运行300 ps(皮秒)。在运行过程中，体系的能量随时间逐步达到稳定状态，沥青分子也在目标温度下由初始状态变为平衡状态。随后，将该沥青分子模型放置于NPT系综下(等温等体积系综)，其中温度设置为533.15 K，压力设置为p=1.0 atm。运行500 ps后，沥青分子体系收缩至稳定状态，达到真实密度。最后，将体系在NVT系综(T=298.15 K)中再运行500 ps，使体系温度达到常温状态，以获得沥青的最终分子结构，如图3所示。考虑到平衡模拟结果的准确性和模拟时间，模拟的时步选择1 fs(飞秒)。

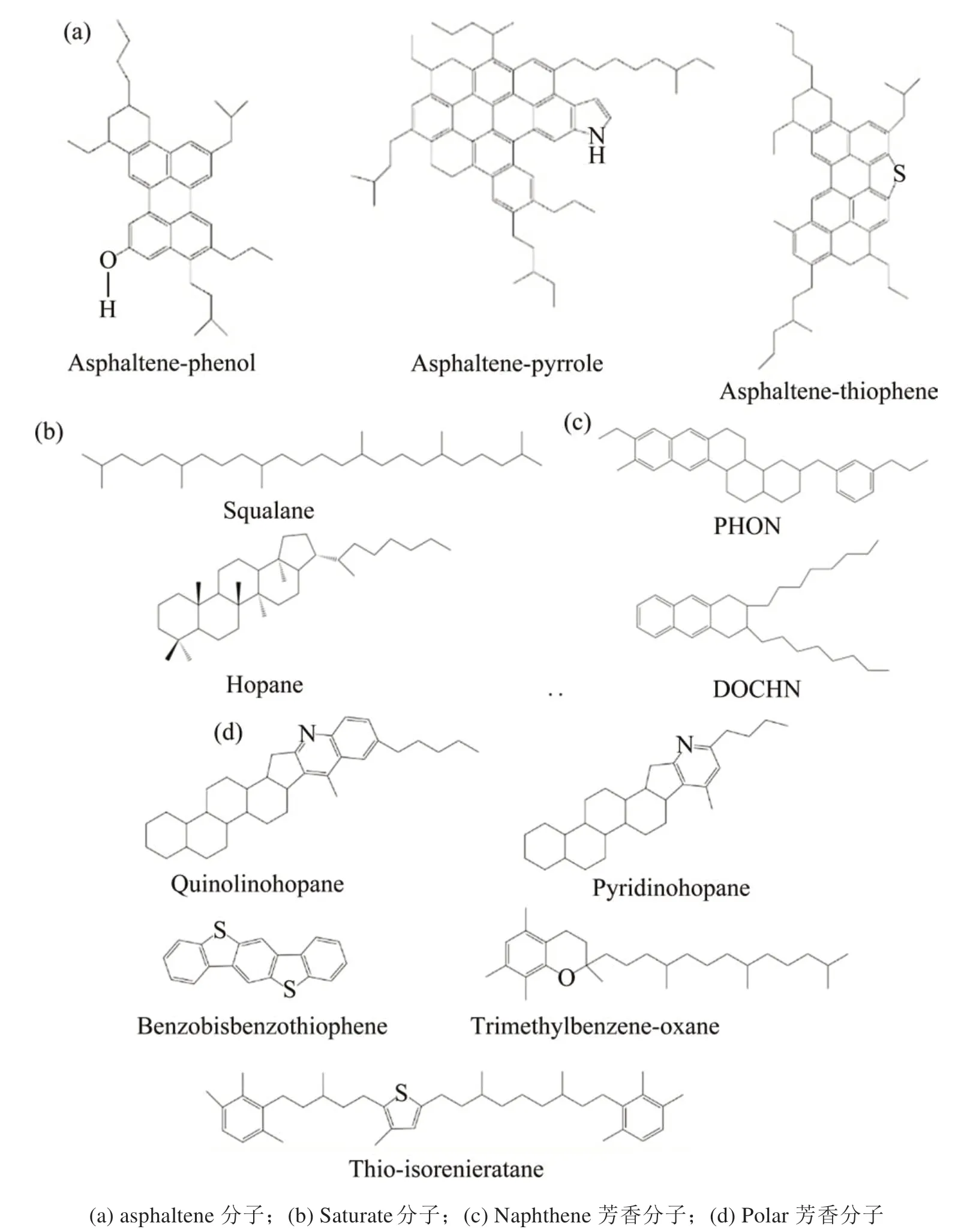
图1 基质沥青分子模型Fig.1 Virgin asphalt model

图2 沥青3组分模型的分子结构Fig.2 Molecular structure of 3 component model of asphalt

图3 2种不同的沥青分子模型Fig.3 Two different asphalt molecular models

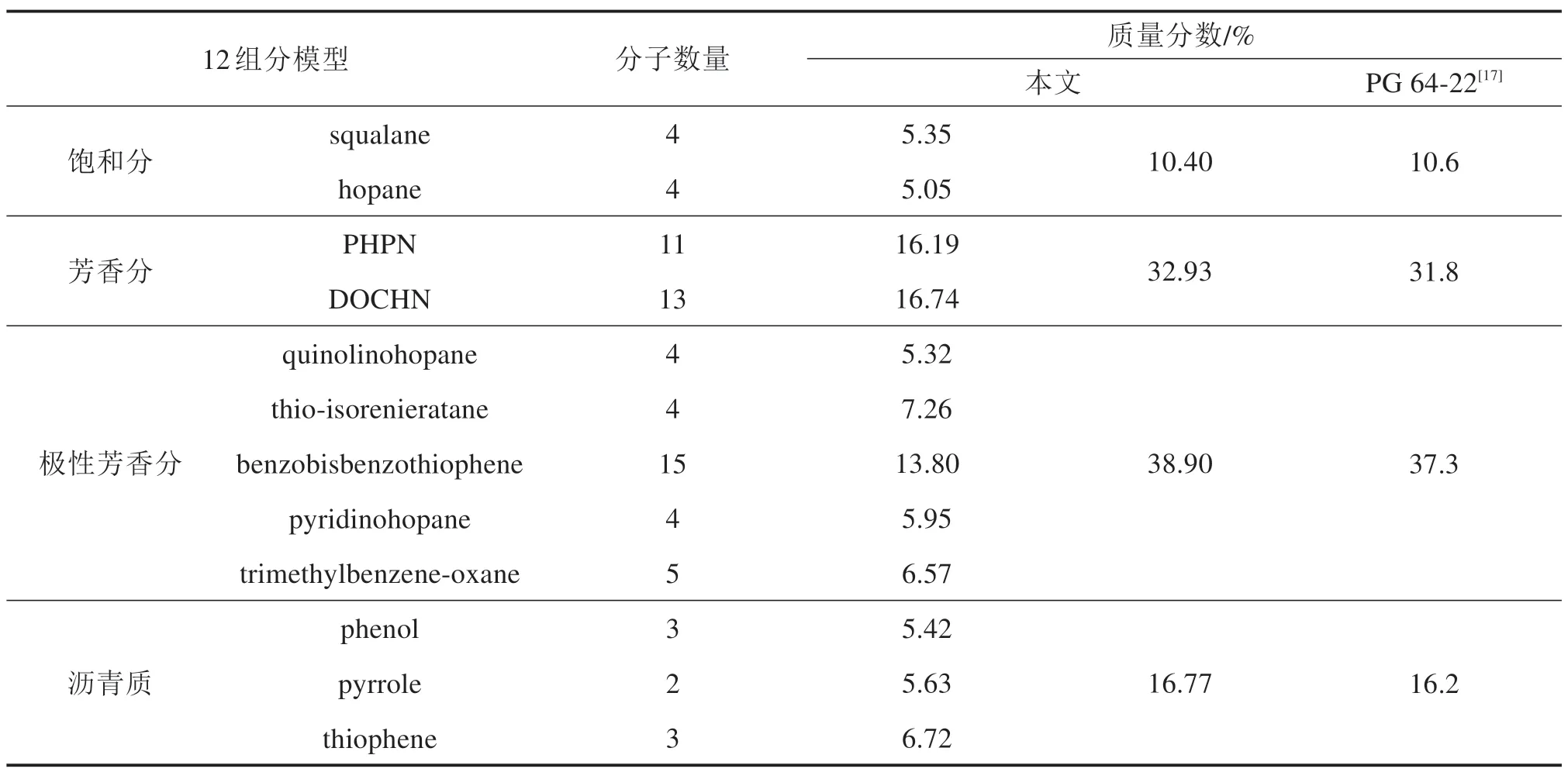
表1 沥青12成分模型分子数量Table 1 Number of molecules of 12 component model of asphalt

表2 沥青3组分模型的分子组成Table 2 Number of molecules of 3 component model of asphalt

1.2 CVFF力场

在MD模拟中，力场在计算分子间的相互作用、键能和非键相互作用中起着重要的作用。力场的选择应根据分子的类型和MD软件的要求。常用的力场包括OPLS力场(Optimized Potentials for Liquid Simulation)、COMPASS力场(Condensedphase Optimized Molecular Potentials for Atomistic Simulation Studies)和CVFF力场(Consistent-Valence Force Field)。OPLS力场注重凝聚相性质的模拟，是模拟生物分子和聚合物的常用方法。COMPASS力场较适用于金属，金属氧化物和金属卤化物，能够预测各种固态性质。已有研究表明CVFF力场适用于各种多肽、蛋白质和有机分子，并能准确表达模拟系统的机制和结合能[18]。该力场包含了氨基酸、水和各种有机官能团的参数，适用于小型有机晶体(酰胺和羧酸等)，气相结构，多肽和蛋白质等有机系统。一系列关于沥青与沥青混合料的研究大多都采用了CVFF力场，具有比较好的适应性[18-19]。CVFF力场的能量表达形式如式(1)所示：

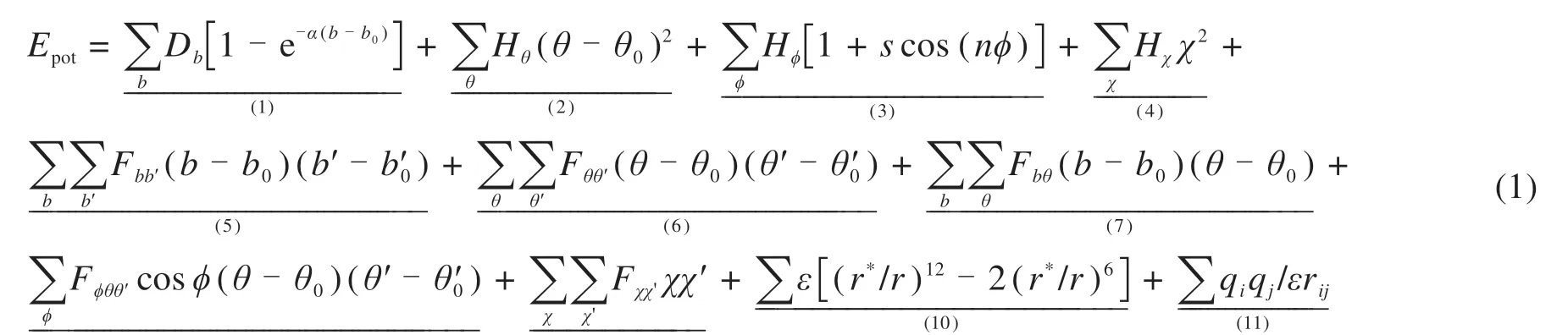
式中：1～4项通常称为力场的对角项，分别表示键长、键角、扭转角和面外相互作用的变形能。5～9项是偏离对角线(或交叉)项，表示内部坐标变形之间的耦合。其中，第5项描述相邻键拉伸之间的耦合。10～11项描述了非键相互作用，其中第10项表示范德华尔与Lennard-Jones函数的相互作用，第11项是静电相互作用的库仑表示，介电常数ε可以与距离有关，是rij的函数。

2 模拟结果与分析

2.1 模型验证

首先，基于MD计算基质沥青的密度，将MD作为直接指标，观察基质沥青模型是否正确，力场的选择是否合理。密度作为基质沥青最重要的材料性质之一，被广泛应用于沥青分子模型的验证[11-19]。本文基质沥青的密度是在NPT集成在目标温度和恒定压力1 atm条件下计算，计算时间为200 ps。每100 fs收集一次密度数据，时间步长为1.0 fs，然后通过平均数据得到最终密度值。图4为基质沥青模型在CVFF力场下与LI等[15]在OPLS力场下的计算数据的密度结果对比。从图4可以看出，沥青的密度与温度之间的关系与Greenfield的测量结果一致，而本文的模拟数据因力场不同而略高。结果表明，当沥青由固相和液相转变时，密度随温度的升高而逐渐降低。随着温度的升高，沥青密度有2个变化点。第1个点(350 K左右)称为玻璃化转变温度，表示沥青模型由玻璃状固体变为黏弹性状态。玻璃温度的计算结果与之前的模拟结果(298.2～385.2 K)一致[15]。第2个点(440 K左右)是沥青变为牛顿流体状态时的液-液转变温度。在298.15 K时，基质沥青模拟密度最高为1.02 g/cm3，在READ等[20]实验测得的1.01～1.04 g/cm3范围内。因此，基于上述模拟结果，采用4组分12成分的基质沥青模型和CVFF力场模拟沥青材料性质是合理、准确的。

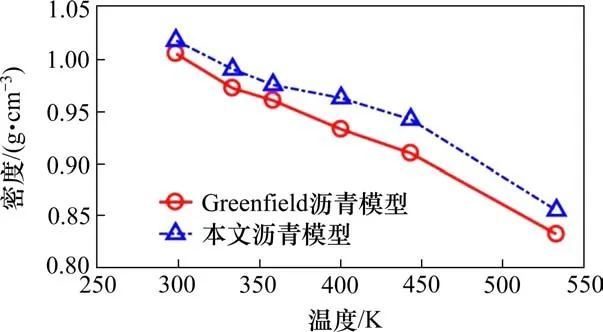
图4 不同温度下的沥青密度使用CVFF力场与使用OPLS力场的Greenfield数据比较Fig.4 Asphalt density at different temperatures using the CVFF force field compared to Greenfield’s data with OPLS force field

2.2 密度对比分析

本文利用分子动力学模拟方法,比较2种沥青分子模型(3组分和4组分12成分分子模型)密度随温度238.15，268.15，298.15，358.15和443.15 K(−35℃，−5℃，25℃和170℃)的变化，这一温度范围涵盖了从寒冷的冬季条件到铺路过程中达到的高低温度范围。每个计算结果都是3次独立模拟的平均值。

模拟结果如图5所示，2种沥青分子的密度都随温度的上升而减小。此外，与3组分沥青分子模型相比，12成分沥青分子在298.15 K的模拟密度为1.02 g/cm3，与READ等[20]的试验结果更为符合。此外，密度斜率的变化表示2种沥青分子模型均存在玻璃态转变行为，同样与实际的试验现象相符。从图6中可以看出，12成分沥青分子转变温度介于268.15 K和358.15 K，而3组分沥青分子模型计算结果则介于298.15 K和433.15 K之间，两者都高于室内试验测得的沥青玻璃态转变温度(低于273.15 K)，这主要是由于分子模拟系统在时间(1 fs=10−12s)和空间(1Å=10−9m)上远小于实际试验，导致需要更高的温度来驰豫沥青分子(即达到热动平衡所需的时间)。

图5 2种不同的沥青分子模型密度随温度的变化Fig.5 Density of two different asphalt molecular models varies with temperature

2.3 黏度对比分析

本文采用平衡态分子动力学模拟方法[21](Green-Kubo)计算2种沥青分子模型的黏度η，如式(2)所示：

其中：V是系统的体积；T是温度；kB是玻尔兹曼常数；Pstab(0)Pstab(t)为应力张量自相关函数；st表示平均等效瞬时非对角应力分量，并从对角线分量中减去压力，从而形成一个无符号的应力张量自相关函数。

图6为沥青分子黏度随温度的变化规律。可以看出，沥青的黏度随着温度的升高而下降，并且12成分沥青的黏度明显高于3组分沥青，与PG64-22型号沥青试验结果相一致。同时，高温条件下(533.15 K)，12成分沥青黏度值约为2.14 cP，3组分沥青黏度值为0.62 cP。其他学者也基于分子动力学方法研究了沥青在高温下的黏度，其中XU等[22]采用Compass力场计算沥青分子的黏度，得到533.15 K下沥青黏度值为3.03 cP，LI等[23]采用OPLS力场计算得到533.15 K沥青黏度为2.2 cP。因此12成分沥青相比3组分沥青更加能够表征实际沥青的流变性质。

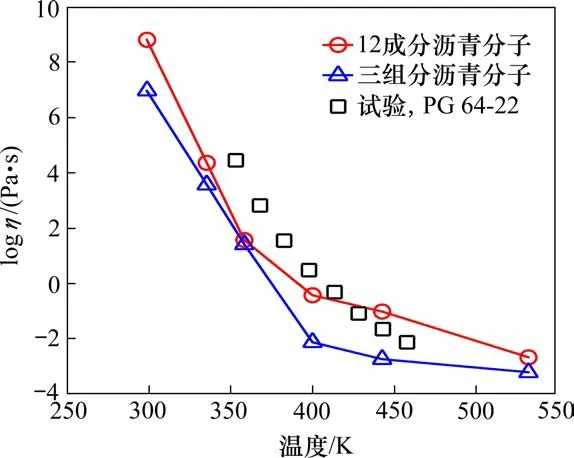
图6 2种不同沥青分子黏度随温度变化模拟结果，以及PG 64-22型号沥青试验结果Fig.6 Simulation results of molecular viscosity of two different asphalt varying with temperature,and test results of PG 64-22 type asphalt

2.4 表面自由能和内聚能密度

表面自由能被定义为分子表面作用力的体现，是指在保持温度，压力和组成不变的条件下，材料增加单位表面积所需的功的大小。表面自由能可以用来衡量当表面产生时分子间相互作用的破坏[24]。表面自由能γa由沥青分子结构与沥青分子层之间的势能差与形成沥青层时的表面积之比得到，如式(3)所示：

其中：Elayer为沥青层的势能；Ebulk为沥青结构的势能；A为增加的单位表面积，由于沥青模型中分子团聚集引起的表面的不均匀，因此本文用Connolly表面积表示增加的单位表面积。Connolly表面积也称为可接近的表面积，由van der Waals表面的所有点组成，2种不同组成的沥青分子模型对应的Connolly表面积如图7所示。

图7 2种沥青分子的Connolly表面积Fig.7 Connolly surface area of the two asphalt molecules

内聚能密度(CED)被定义为单位体积的内聚能，是评价分子内部作用力大小的一个物理量，主要反映基团间的相互作用。一般来说，分子中所含基团的极性越大，分子间的作用力就越大，则相应的内聚能密度就越大，因此用内聚能密度来衡量分子之间的相互吸引性，用以评估沥青分子模型中分子间的相互作用。内聚能密度的值根据溶解参数计算，如式(4)和式(5)所示。溶解参数为最小化整个体系的Gibbs自由能，将溶剂与溶质的相互作用量化为分离溶剂和溶质分子[25]。

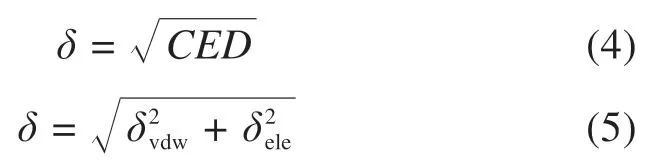
其中：δ是溶解参数；δvdw和δele分别是范德华力和静电相互作用的贡献。

表3为2种沥青分子模型的基本属性，可以看出沥青分子的模拟结果与试验结果或其他学者研究结果均相符。但是由于12成分沥青的分子种类和数量更多，导致其Connolly表面积和表面自由能均大于3组分沥青。同时，3组分沥青的内聚能密度和溶解参数值也略低于12成分沥青，表明12成分沥青中组分间的极性更高，分子间的相互作用更强，且该沥青体系的扩散能力(外部分子进入沥青分子中)比3组分更弱。

表3 基于分子动力学模拟计算2种沥青分子模型的属性Table 3 Properties of the two asphalt molecular models were calculated based on molecular dynamics simulation

3 结论

1)2种沥青分子的密度随温度的变化趋势一致，都随温度的上升而减小，但是12成分沥青分子模型在各个温度的模拟值比3组分沥青分子模型大约高0.09 g/cm3，也更能代表宏观试验下沥青的密度变化。

2)基于平衡态分子动力学模拟方法计算了沥青分子的黏度。黏度变化曲线体现了沥青随温度变化的玻璃态转变行为。12成分沥青分子在低温阶段更能体现实际沥青的流变性质，而3组分沥青分子与实际沥青黏度变化在高温阶段(大于433.15 K)更吻合。

3)3组分沥青结构的分子间作用更符合实际。由于12成分沥青含有更多的分子类型以及极性分子，因此其表面自由能和内聚能密度高于3组分沥青，也略微高于试验值。

4)通过模拟计算结果与试验结果的对比，表明采用CVFF力场可以较为合理地模拟计算沥青的热力学特性。