基于BCH 纠错算法的编解码器设计与实现*
王莞,魏敬和,于宗光
(1.江南大学 物联网工程学院,江苏 无锡 214122;2.中国电子科技集团第58 研究所,江苏 无锡 214072)
0 引言
Nand Flash 是一种非易失性存储器,与NOR Flash 相比具有读写速度快和存储密度高等优势,但由于NAND Flash 本身结构特点,其存储单元出现数据位翻转现象比NOR Flash 中更常见[1],与此同时,随着NAND Flash技术的飞快发展,NAND Flash 从SLC 结构发展为MLC结构及现在的TLC 结构,每个存储单元可以存储2 bit 以至更多的数据,使得数据位之间的相互干扰变大,进而导致出错概率增大,随着工艺水平的不断提高,超深亚微米下的电荷效应进一步增加了数据出错的可能性。因此,在对NAND Flash 存储数据时,必须采用更高的纠错技术,以提高存储的稳定性。文献[2]中采用一种8 位并行BCH 编解码器,但因为电路并行处理数据少,影响处理速度,文献 [3] 中设计一种纠错16 位的BCH 编解码器,但纠错位数较少。文献[4]中设计一种校正32 位出错位的BCH 编解码器,相比较纠错位数有所增加,但还不能满足大容量存储的数据校正。本文设计一种16 位并行BCH 编解码器,并且具有最高48 位纠错能力,纠错速度和纠错能力都有了进一步的提高。
1 BCH 编码基本原理
矩阵BCH 码是纠正多个随机错误的循环码,可以用生成多项式g(x)的根来描述。它是一种有限域中的线性分组码,广泛应用于存储和通信领域中的编码。定义如下:给定任一有限域GF(q)及其扩域GF(qm),其中q 是素数或素数的幂,m 为某一正整数。若任一码元取自GF(qm)上的循环码(n,k),其中n=2m-1,其生成多项式g(x)具有2t 根{a1,a2,…,a(2t-1),a2t}时,t 位 数,则 由生成多项式g(x)生成的循环码称为q 进制BCH 码,记为(n,k,t)[5]。最常用的BCH 码通常为二进制的BCH 码,二进制BCH 码的码元都是由0 和1 构成的,便于硬件电路的实现。本文以下讨论的BCH 码是二进制BCH 码,二进制本原BCH 码有以下重要参数,码长为n=2m-1,信息长度为k,纠错位数量为t,校检码长度为mt=n-k,对于本设计中,k=1 024 B=8 192 bit,t=48,n=8 192+48×14=8 864,因此BCH 码为(8 864,8 192,48),其中,校检码长度为672 bit。
2 BCH 并行编码器设计
BCH 编码可以按如下方式构造,假定信息多项式为:
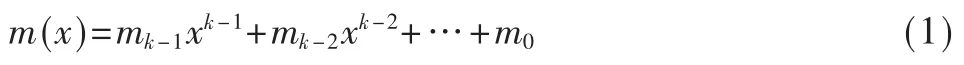
其中,mi∈GF(2),BCH 码系数通常由计算机离线生成,首先找到生成多项式g(x),记为:
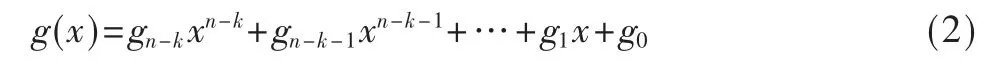
则BCH 编码后的码组c(x)为:

其中校检多项式为:

由n-k=672,故r(x)=(x672m(x))mod g(x)进行16 位并行编码,记k=L·m,L=512,则有:
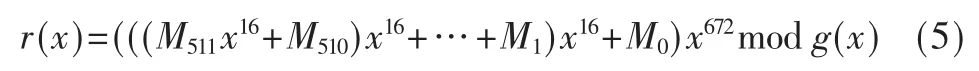
可以得到迭代计算的关键方程式:
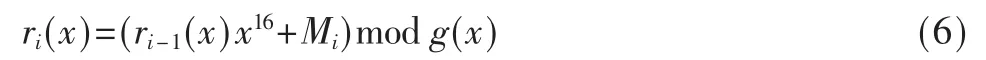
所以BCH 编码的实质就是有限域内以生成多项式为模的除法问题,是将xn-km(x)对生成多项式g(x)求模,可以通过线性移位寄存器(LFSR)来实现,16 位并行编码器原理结构如图1 所示。
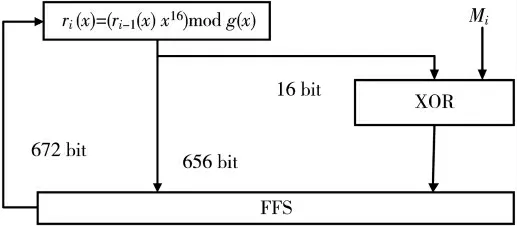
图1 16 位并行编码器结构
16 位并行BCH 编码器工作流程如下:
(1)在编码开始之前,把所有寄存器初始化为0;
(2)把ri(x)=(ri-1(x)x16+Mi)mod g(x)式做循环迭代运算,Mi即为当前时刻要输入到Nand Flash 中16 位数据,信息比特按照从高位到低位的方式依次进入。
(3)迭代到512 次的时候进入另一个阶段,这时设置输入Mi=0,再继续迭代计算42 次,就完成并行编码的计算,BCH 编码寄存器储存的值即为最终校检位。
BCH 编码过程包含3 个状态,分别为空闲状态(IDLE)、编码状态(ENC)、校检因子传输状态(WRITE)。在复位信号为低电平时,状态机都被转入IDLE 状态,在时钟上升沿,纠错使能信号enable_ecc 为高电平,dir_sel 信号为低电平并且码字有效信号data_in_valid 为高电平时转入ENC 状态;当1 024 B 数据编码完成后进入WRITE 状态,当完成校检因子传输后回到IDLE 状态,其状态转换图如图2 所示。
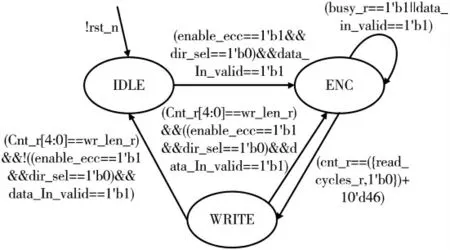
图2 编码过程状态转换图
3 BCH 译码器设计
在所有的BCH 译码算法中最常用是Berlekamp-Massey 迭代算法(简称BM 法),BCH 译码器首先通过计算校检因子实现错误检测,然后通过无逆BM 迭代算法和钱氏(Chien)搜索法实现纠错,译码过程主要分为以下三个步骤完成[6],BCH 译码流程如图3 所示。
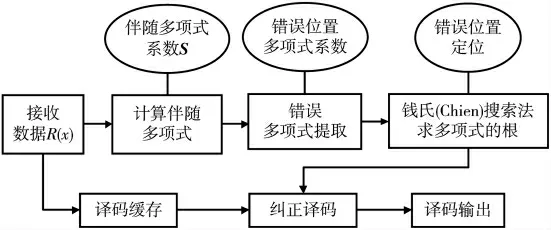
图3 BCH 译码流程
第一步:由接收到的R(x)计算伴随多项式S=(s1,s2,s3,…,s2t),求出伴随式系数。
第二步:根据伴随多项式S 求解错误多项式σ(x)=σtxt+σt-1xt-1+…+σ1x1+1,进行错误多项式系数提取。
第三步:求解σ(x)的根,利用钱氏(Chien)搜索法进行错误位置定位,并进行错误纠正。
3.1 伴随多项式计算
假定发送的码字为:
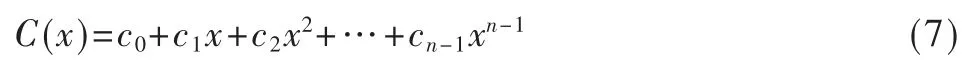
接收到的码字多项式为:
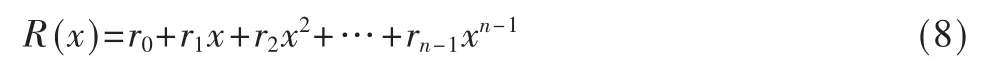
假设错误多项式为:
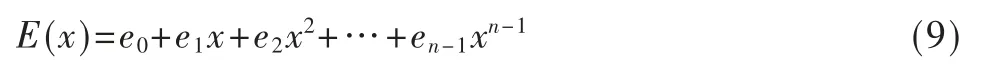
理论上,任何一个接收码字R(x)均可看作发送码字C(x)与错误多项式E(x)的叠加[7],即:
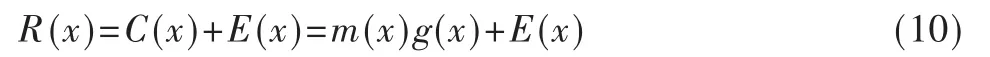
由于ST=HRT,其中H 为校检多项式,因此伴随多项式可以表示为:

由于aj(j=0,1,2,…,2t)是生成多项式g(x)的根,因此,当x=aj时,可得到伴随多项式的系数为Sj=R(aj)=mj(aj)g(aj)+Ej(aj)=Ej(aj),伴随多项式S=(s1,s2,…,s2t)的计算转换为R(x)除以g(x)的除法运算,相除之后的余式即为伴随式,如果伴随多项式中任意一个元素Sj不为0,则表明有错误,否则没有错误。
伴随式电路硬件实现如下:

上式展开得:

16 位并行伴随式电路结构如图4 所示,每个时钟周期可以处理16 bit 数据,其中,乘法器和加法器均为有限域乘法器和有限域的加法器,因为有限域的加法采用模2 进行运算,故加法器为直接的异或运算。在GF(214)域多项式的乘法过程和一般多项式乘法一样,在各项相加的时候按照模2 规则进行,运算过程出现大于a14项需要通过GF(214)域上的本原多项式x14+x10+x6+x1进行高位消除[8]。首先计算S=(S1,S3,…,S2t-1),然后由于伴随系数满足,通过计算得到S=(s2,s4,…,s2t)。由此可得伴随多项式为:

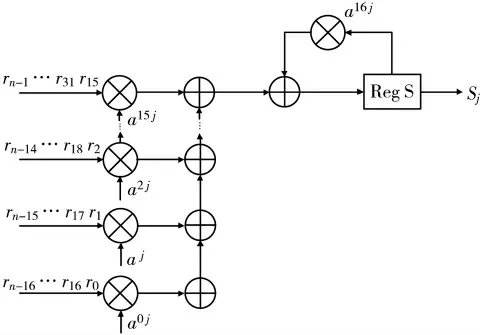
图4 并行伴随式电路结构
BCH 译码首先要进行伴随多项式求解,伴随多项式计算作为流水线的第一级,设计伴随式模块有三个状态分别为空闲状态(SYN_IDLE)、接收码字状态(READ)、伴随式计算状态(SYND_CALC),在复位信号为低电平时,无论伴随式模块在何种状态,都被转入SYND_IDLE 状态,在时钟上升沿,纠错使能信号enable_ecc 和码字有效信号data_in_valid 为高电平时转入READ 状态。当伴随式模块处READ 状态,计数信号cnt_syn_r 为1 024 时,进入SYND_CALC 状态。当在伴随计算状态,如果cnt_syn_r=6′b101110 并且data_in_valid 为低电平时,表明伴随式计算完成,伴随式计算模块转入SYN_IDLE 状态;如果伴随式系数有一个不为零,表明接收码字有错误,需要进入后续的错误位置多项式和钱氏搜索操作,伴随式计算状态转换如图5 所示。
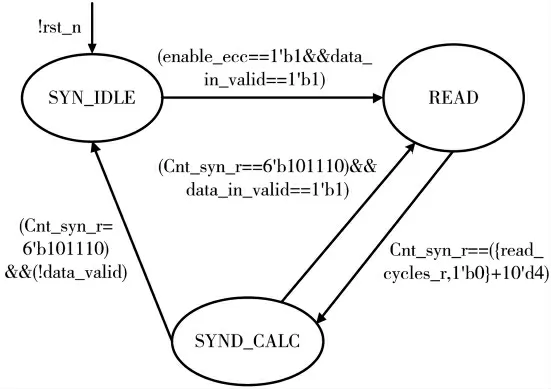
图5 伴随多项式计算状态转换图
3.2 错误多项式提取
求解错误位置多项式是BCH 译码过程中最重要的一步,首先构造错误位置多项式如下所示:σ(x)=σtxt+σt-1xt-1+…+σ1x1+1,其中,错误位置为该式的根,由数学推演,可知错误多项式的系数σt,σt-1,…,σ2,σ1和伴随式有如下关系:
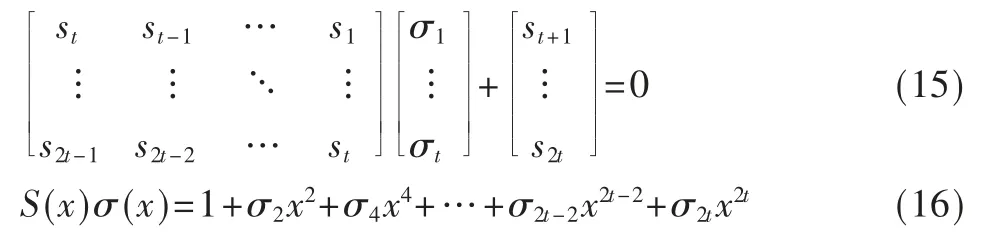
将S(x)和σ(x)带入上面方程式得到σ(x)的关键方程[9]:

由于BM 算法迭代效率,易于硬件实现,本文采用基于二进制BCH 码的无求逆BM 迭代算法求解该方程,首先选择一组合理的初始值σ(0)(x)和ω(0)(x),经过第一次迭代运算求得σ(1)(x)和ω(1)(x)[10],依次类推,由σ(i)(x)和ω(i)(x)求得σ(i+1)(x)和ω(i+1)(x)。迭代过程中定义第j+1 和第j 步的差值为dj,则有:


3.3 钱氏搜索法定位错误位置
通过上面的BM 算法,能够得知错误位置多项式为σ(x)=σtxt+σt-1xt-1+…+σ1x1+σ0,如果直接对上式进行因式分解[13],将得到σ(x)的分解等式:
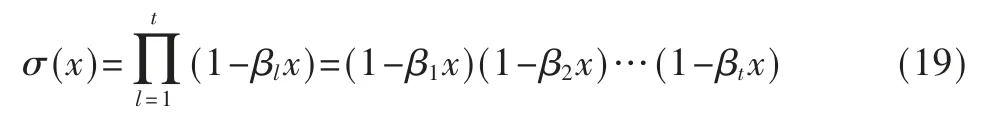
随着t 的值变大时,会发现求σ(x)的因式分解越来越困难,因此通常采用钱氏搜索法求出上式方程的根。钱氏搜索法原理如下[14],当x=1/β1时,σ(x)=0,其中x 的取值范围为ai,i=n-1,n-2,…,0。因此,将ai依次带入σ(x),如果σ(x)=0,则ai为根,说明第i 位发生了错误[15]。
BCH 译码过程第三级通过钱氏搜索法进行错误位置定位并进行纠错,钱氏搜索过程包含四个状态分别为钱氏搜索空闲状态(CHI_IDLE)、接收码状态(CHIEN_NC)、搜索状态(CHIEN)、错误信息发出状态(STIG)。开始chien_state_next 寄存器为SYND_IDLE 状态,在时钟上升沿,chi_err_r 信号变为高电平后,状态机跳转到CHIEN_NC状态。当cnt_chi_r 搜索计数信号满足时,chien_state_next为CHIEN 状态;在钱氏搜索找到错误总数chi_cnt_err_r信号等于cnt_exp_err_r 信号时,完成钱氏搜索chien_state_next 进入STIG 状态,在下一个时钟上升沿dec1_full 信号满足为低电平时,chien_state_next 回到CHI_IDLE 状态,钱氏搜索状态转换如图6 所示。
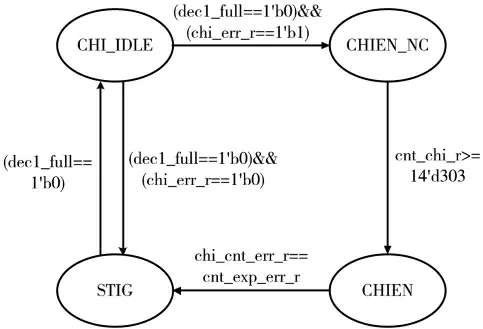
图6 钱氏搜索状态转换图
4 仿真与验证结果分析
利用Verilog 语言完成上述电路模块的RTL 级设计,在Linux 系统下利用VCS 工具进行电路的仿真与验证。发送8 192 比特信息位,通过BCH 并行编码器电路生成672 位校检码,编码过程仿真波形图如图7 所示。完成编码后本文通过后门访问FIFO 寄存器把1、3、5、7、9、11 字节的数据翻转,共产生48 位错误,然后再通过BCH 译码器分别进行伴随式因子的计算,错误多项式系数提取,最后通过Chien 搜索法找到发生了错误位置的定位并正了错误值,伴随多项式计算与错误多项式提取仿真波形图如图8 所示,钱氏搜索仿真如图9所示。

图7 并行编码过程仿真波形图
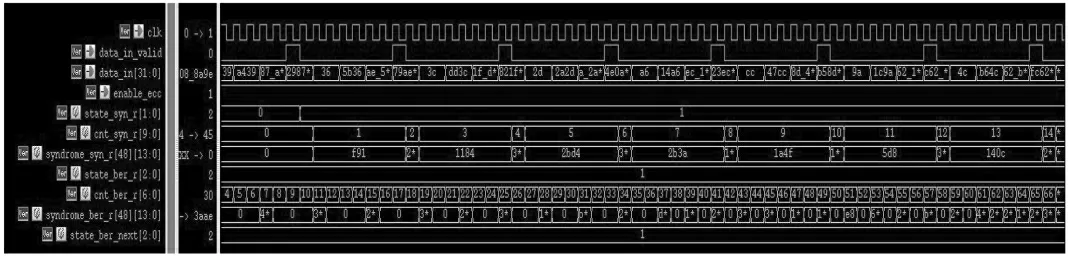
图8 伴随多项式计算与错误多项式提取仿真波形图
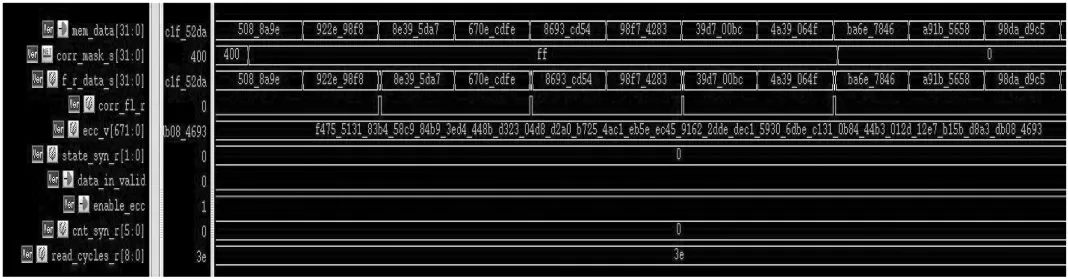
图9 钱氏搜索仿真波形图
5 结论
本文对编译码电路采用高效16 并行电路结构,与此同时译码过程采用流水线结构,BCH 解码器可以在从内存中读取数据时检测错误,提出了一种对于Nand Flash 的48 bit 纠错能力解决方案,同时减少资源的消耗,减少编解码和解码周期。与其他文献中编解码中的数据传输速度、工作频率与纠错能力对比如表1 所示。今后在此基础上研究AES 加密算法,实现对数据的加密和解密方面有进一步研究。

表1 纠错能力及频率对比

