一种基于改进的马尔可夫链的交通状况预测模型

周明升，刘抒扬

(1.上海外高桥保税区联合发展有限公司，上海 200131；2.上海商学院 商务信息学院，上海 201400)

0 引言

确定了用户的出发地和目的地后，准确预测各条可能路线未来某段时间(行驶到达路段时)的交通状况，可以为用户推荐最优出行线路，减少行驶时间，也方便用户私家车与公共交通的选择。某段线路上的行驶时间应综合考虑以下几个因素：路线本身的情况、行驶到该路线上时的交通流量和驾驶员的驾驶习惯等。当前对交通状况、路线推荐的研究主要有以下几类：(1)基于交通分析的方法[1-2]：通过道路上的识别器及车流量信息，通过“识别器-车流量-行驶方向”的范式来研究交通状况推荐路线，这种方法准确性的前提是要有足够的识别器和车流量信息，数据获取比较困难[3]。通过获取车辆信息，估计实时交通流量，预测将来的交通状况[4-6]，其基于路段的分析需要借助大量数据进行分析，当采样率低、数据稀疏时无法准确估计。(2)基于交通模式学习的方法：给出了概率为基础的方法，通过用户历史GPS 轨迹数据，预测驾驶员的目的地和行车路径[7-8]。其通过学习GPS 轨迹数据来获取驾驶和速度模式计算最快路线[9-10]。(3)智能推荐：试图挖掘驾驶员道路选择的倾向，通过人机交互或推理模型推荐个性化路线，其推荐路线没有随行驶时间而优化[11]。其通过GPS 轨迹数据，寻找关键节点和关键路线，结合用户行为，推荐最快线路[12-13]。

与之前的研究不同，本文的研究通过配置了GPS 的出租车作为交通状况的接收器，获取历史交通路况和实时交通路况信息，通过多阶马尔可夫链模型预测未来的交通状况。出租车的GPS 日志信息既反映了不同时间、不同道路的交通状况，也体现了出租车驾驶员的智慧，可以体现驾驶员的行为习惯。本文不是直接从GPS 轨迹数据中直接分析道路行驶速度和驾驶员驾驶模式，而是通过马尔可夫链来预测某些路线将来某段时间的交通状况。预测过程中，将多阶马尔可夫链转化为一阶马尔可夫链，提高了运算效率和用户响应速度。

1 模型建立

1.1 变量定义

假设交通状况服从m 阶马尔可夫链，模型中相关概念、变量定义如表1 所示。

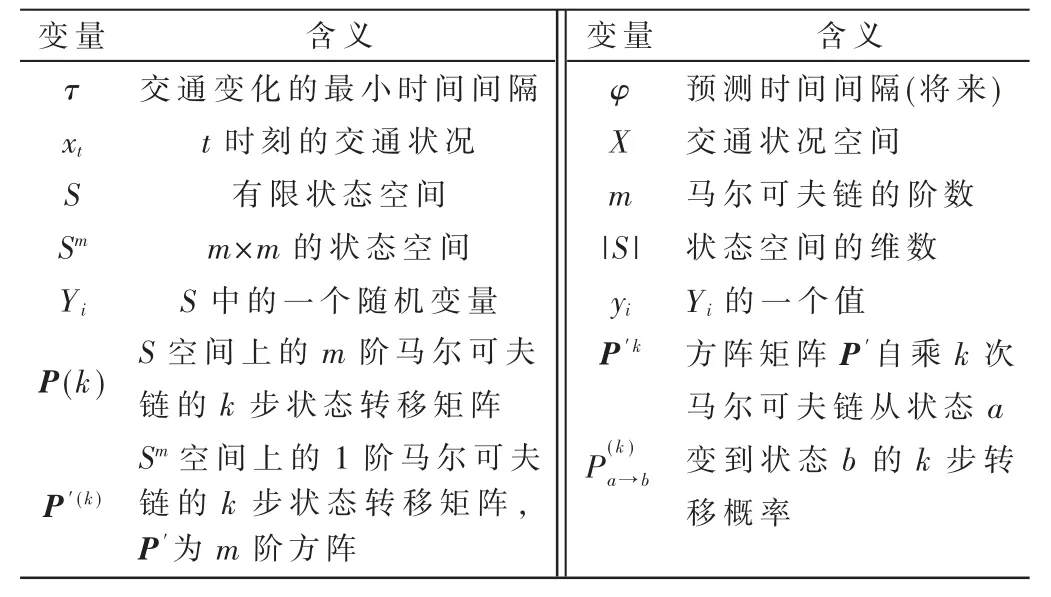
表1 变量定义

1.2 问题描述

交通状况预测模型框架如图1 所示。其中，H 表示历史交通状况，R 表示实时交通路况，F 表示将来的交通状况。本文要做的是用历史交通状况(H)和实时交通路况(R)，预测将来某段时间的交通路况(F)，即H+R→F。

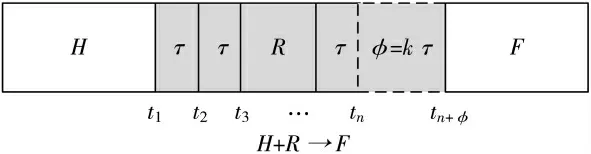
图1 交通状况预测模型框架

时间间隔定义为：

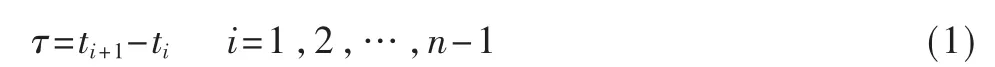
根据实际交通状况，最小时间间隔τ 通常是固定的(是外部变量，由交通系统自身决定，如10 min、15 min、30 min 等)。预测间隔φ 由用户查询时输入，为最小时间间隔τ 的整数倍，即：

根据上述定义，问题转换为已知历史交通状况和当前交通状况，如何预测第k 段(即将来kτ 时间)路况的问题。根据模型假设，如果已知历史交通状况和当前交通状况，求得初始转移概率矩阵和k 步状态转移矩阵，便可求得时间间隔φ 时的交通状况。于是，∀yi∈S，i=1，2，…，n，本文将问题转换为：根据已知分布集合，预测Ym+k的分布，得到转移矩阵：

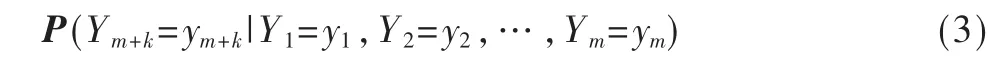
其中，m 和k 是关键指标，m 根据历史数据测算得出或事先给出，k 由用户输入的时间间隔决定。

1.3 实验模型

建模和计算过程如下：

(1)用贝叶斯概率模型计算S 空间的m 阶马尔可夫链的1 步状态转移矩阵P(1)。

根据贝叶斯模型理论，状态转移矩阵P(1)可由下面公式求出：

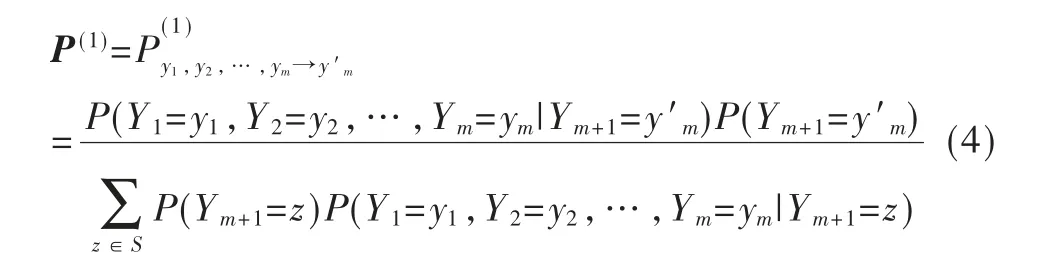
举例说明如下，假设状态空间S={1，2}(其中1 表示畅通，2 表示拥堵)，通过历史GPS 数据可计算得出某路线的初始转移概率，得到转移矩阵P(1)，如图2所示，其中第1，1行第2列的值P1，1→2=0.125表示从状态{Y1=1，Y2=1}到Y3=2的概率。P1，1→2及P(1)中其他元素的值由贝叶斯概率公式求出。

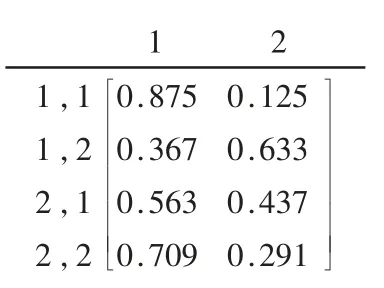
图2 P=P(1)

(2)通过变量的矢量化处理，将m 阶马尔可夫链转换为Sm空间1 阶马尔可夫链。

将S 空间上的m 阶马尔可夫链转换为Sm空间1 阶马尔可夫链[14]，可以简化运算，转换过程如图3 所示。

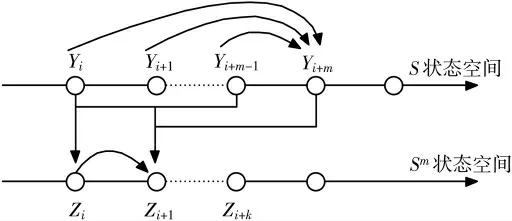
图3 将S 空间上的马尔可夫链转换为Sm 空间的马尔可夫链

接下来，本文计算Sm空间上Zi的1 步状态转移矩阵，计算公式如下：

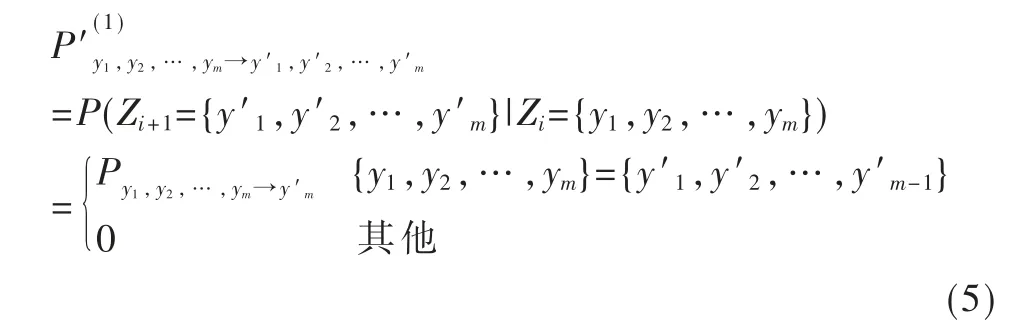
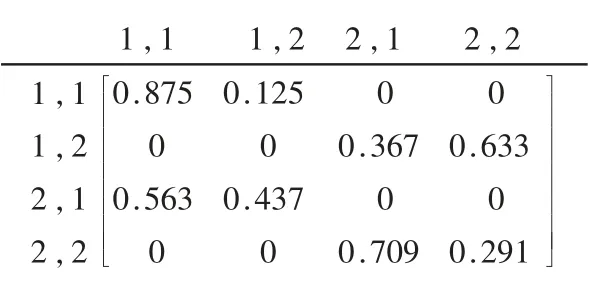
图4 P=P′(1)

(3)计算Sm空间上数列Zi的k 步状态转移矩阵。

根据Chapman-Kolmogorov 方程[13]，Sm空间的Zi的k步状态转移矩可以由矩阵P′自乘k 次得到(P′(k)=P′k），即：

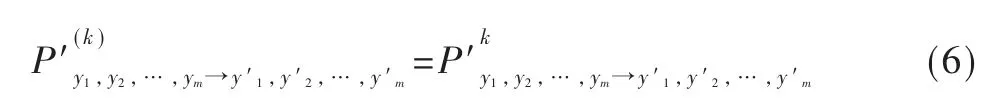
如果k=4，则步骤(1)中在Sm空间的k 步状态转移矩阵转换如图5 所示。

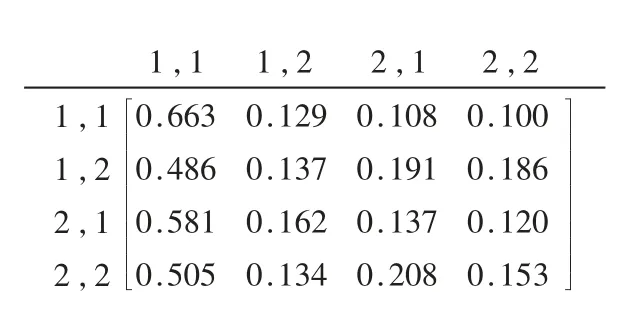
图5 P′(4)=P′4

(4)将步骤(3)的结果，转换为S 空间中m 阶马尔可夫链的k 步状态转移矩阵P(k)。

这一步可以看作是步骤(2)的逆运算，状态转移矩阵计算方法为：

①当1＜k＜m 时，

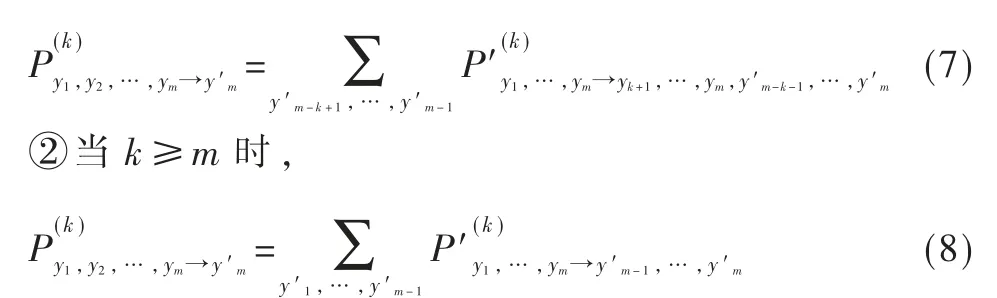
根据上述公式，步骤(1)例子的k 步状态转移矩阵(k=4)如图6 所示。

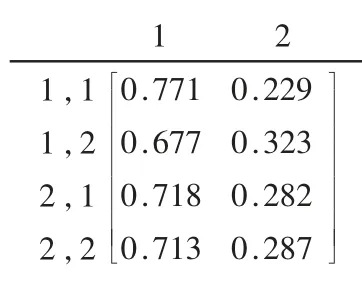
图6 P=P(4)

1.4 模型分析

根据上述模型过程，本文先根据历史记录计算S 空间中马尔可夫链{Yi}的1 步状态转移矩阵P(1)，当k ＞1 时候，状态转移矩阵P′(k)和P(k)可由上述步骤求得[15-16]。计算P(k)的时间复杂度为O(k·|S|∈m)(其中∈＜2.376)，这样要比全部用贝叶斯概率模型计算效率高。实际应用中，马尔可夫链的阶数m 和状态空间S 的阶数通常是比较小的(如m≤3，|S|≤5)，所以，步骤(2)～步骤(4)的计算采用在线计算方式，以提高用户相应速度。

计算得出状态转移矩阵后，本文将得到未来某段时间(φ=kτ)的路况，结合用户的行为分析，可以计算通过某段线路的时间，进而进行最优路线推荐。

2 实验分析

2.1 数据来源及参数配置

(1)数据来源

本文使用的数据来自微软GeoLife 项目的公开数据集。它记录了北京市超过33 000 辆出租车连续3 个月的GPS 日志数据，行驶里程超过4 亿公里，GPS 日志点超过7.9 亿个，平均间隔为3.1 min，相邻点平均距离约600 m[12]。本文用前两个月的数据作为训练集，抽取第3个月的数据作为测试集。本文抽取了10 个工作日、天气状况良好、5 条道路的所有GPS 数据作为测试数据集，样本平均时间间隔3.2 min，相邻点平均距离627 m。

(2)参数配置

实验中，本文定义最小时间间隔τ 为15 min，预测时间间隔φ 为τ 的整数倍(如15 min、30 min 等)(即k 取1，2等)，马尔可夫链的阶数m 取1、2、3、4，分别进行测试。

2.2 模型评价

2.2.1 比较对象

本文的预测方法分别与T-Drive 方法[12]、ARIMA 方法[13]进行比较。ARIMA 方法是著名的交通状况基础预测方法，它依靠当前交通状况信息(通过GPS、高速公路探测器等获得)，预测将来某段时间的交通状况；T-Drive方法通过对历史GPS 日志信息的分析，挖掘交通模式，然后根据其分布预测某时段、某路线的交通状况。

2.2.2 评价方法

本文用均方根误差(Root Mean Square Error，RMSE)来评价预测结果的准确性，定义：

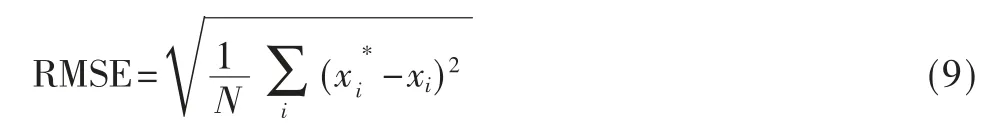
(1)预测时间：分别用本文的预测模型和其他预测模型来预测将来某时间段、某段路线(可以是道路的组合)的通过时间。

(2)基准行驶时间：考虑到工作日与非工作日、时间段、天气状况、驾驶员经验等因素对行驶时间的影响，本文选择同一时间段、同一线路上所有出租车(配置了GPS)的平均通过时间作为基准通过时间(xi)。

2.2.3 评价结果

本文分别用时间段、不同时间间隔φ(因为φ=kτ，τ由外部因素决定，k 变化引起φ 的变化)下3 种方法的RMSE 进行比较(根据RMSE 的定义，RMSE 越低，预测的准确率越高)，然后分析m(马尔可夫链的阶数)取值不同，对本文的模型预测结果准确率的影响。

图7 描述了时间间隔φ 固定时(实验中φ=60 min)，3种方法在工作日不同时间段的RMSE 值。结果显示，本文方法比ARIMA 方法和T-Drive 方法要优异，特别是高峰时段(AM7:30-AM9：30)。

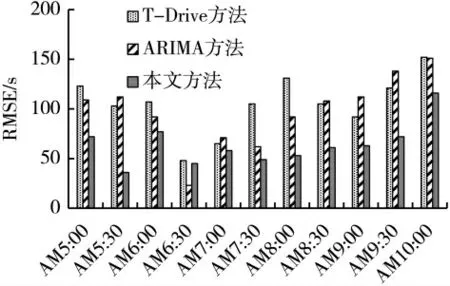
图7 φ=60 min 时，3 种方法的RMSE 比较

图8 描述了时间间隔φ 对预测误差的影响。随着时间增加，3 种方法的误差都在增大，但本文的方法误差更小。换句话说，在相同的误差要求下，本文可以预测更长时间的交通状况。

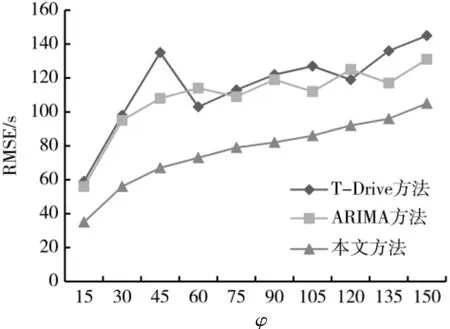
图8 φ 取不同值下3 种方法的RMSE 比较(τ=15 min)

图9 描述了马尔可夫链的阶数选择对准确性的影响。结果显示，其他环境不变时，m 取值越大，结果越准确。这与时间情况是一致的，一段时间以后的交通状况不仅受到当前交通状况的影响，也受到之前若干时间交通状况的影响。但m 取值越大，意味着计算的难度越大。

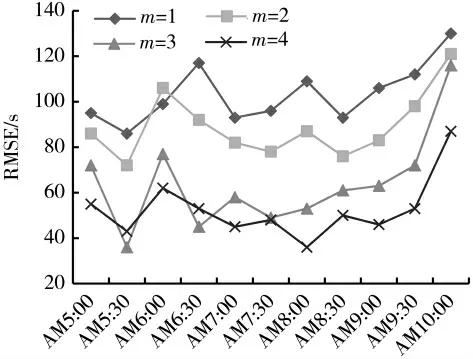
图9 m 的不同取值对RMSE 的影响

3 结论

准确预测未来某段时间的交通路况是进行路线推荐的前提和关键，本文提供了一种基于多阶马尔可夫链的交通状态预测方法。作为一个对实用效果要求很高的课题，为提高模型运算速度，提高对用户的响应速度，对历史数据进行预处理、预计算(初始状态转移矩阵等结果存放在服务器中)，确定好用户的始发地和目的地后，本文对其各条可能路线、未来某段时间的交通路况进行在线运算。运算过程中，本文将多阶马尔可夫链转换为一阶马尔可夫链，进一步提高了运算效率。实验表明，即使采用较小的阶数，也可以得出比较准确的结果，因此本文的方法是行之有效的。