回转体高速入水弹道模型研究
焦伟鹏,黄振贵,陈志华,刘想炎,王浩,周可
(南京理工大学 瞬态物理国家重点实验室,南京 210094)
入水问题是流体力学研究的一个重要领域,在自然学科和工程技术中有着广泛的应用前景,其中回转体高速入水是近几年的聚焦热点。回转体在高速入水过程中,涉及到入水冲击、超空泡流动和流固耦合等物理现象,这使得回转体在运动过程中的运动轨迹和姿态难以预测,空泡形态多变。因此,需要建立回转体高速入水的弹道预测模型,为分析回转体在高速入水过程中的空泡和弹道特性提供一种有效方法。
超空泡是回转体高速入水系统的重要组成部分。Logvinovich等和Basharoua等基于势流理论和试验结果提出了空泡截面独立扩张原理,该理论反映了细长体超空泡流动的本质与主要特征,能够同时适用于定常和非定常超空泡流,为空泡流研究提供了一种简单的研究方法。基于空泡截面独立扩张原理,Savchenko等展开了大量超空泡流动的试验,结合试验数据和理论分析,不仅得到了描述超空泡流动主要特征参数的理论公式和半经验公式,还验证了该理论的正确性和有效性。Guo等基于Rayleigh-Besan问题的理论解析和试验研究,建立了回转体高速入水的空泡形态计算半经验公式,该公式能够有效地适用于定常和非定常回转体高速入水。孟庆昌等通过数值模拟研究了3种不同头型射弹的高速垂直入水空泡特性,对比了弗劳德数与空泡面闭合无量纲时间的关系,发现亚声速射弹的空泡面闭合无量纲时间基本保持不变。马庆鹏等对射弹高速入水时空泡的发展规律、深闭合特性等进行了数值模拟研究,通过分析入水弹道与空化流场的变化规律,获得了射弹入水参数对入水过程中压力、密度场和速度场的影响规律,并给出了各流场的仿真计算结果。
回转体高速入水后,受不同运动初始参数和结构设计参数的影响,回转体的流体动力多变,弹道特性复杂。张宇文等系统研究了回转体在超空泡状态下的流体动力,应用细长体理论和切片法得到了超空泡弹体的流体动力计算公式,通过数值模拟分析了位置力、阻尼力系数的变化规律,并通过局部相似试验研究了模型尾部的流体动力特性。Gao等通过数值模拟研究了射弹不同入射角和入水攻角高速斜入水的空泡形态和弹道特性,发现在小入射角的情况下,弹体会接触空泡壁面,形成周期性尾拍运动,振幅随射弹入射角度和长径比的增大而减小。侯宇等通过试验研究了射弹小角度高速入水过程中的弹道特性,分析了弹体不同侧滑角入水冲击过程的弹道轨迹、喷溅演变和水下压力波传播特征,发现在高速入水过程中,增大射弹侧滑角,会降低射弹入水弹道的稳定性。目前高速入水的研究方法主要集中在试验和数值模拟方面,关于回转体高速入水弹道模型的研究相对较少。
本文针对回转体高速入水问题,基于空泡独立扩张原理,考虑空泡的记忆效应,建立了一种回转体高速入水的弹道预报模型。与相关试验结果进行对比,验证了该弹道模型的准确性,并分析了回转体高速入水过程中空泡的形态发展和弹道特性。
1 回转体高速入水弹道模型建立
1.1 运动方程
如图1所示,建立地面坐标系()和弹体坐标系()。地面坐标系原点置于水平面入水点,轴平行于水平面,轴正方向垂直水平面向上。弹体坐标系原点位于回转体重心处,轴正方向沿回转体轴线指向回转体头部,轴正方向垂直轴向上。轴与轴的夹角为回转体俯仰角,位于轴上侧为正。
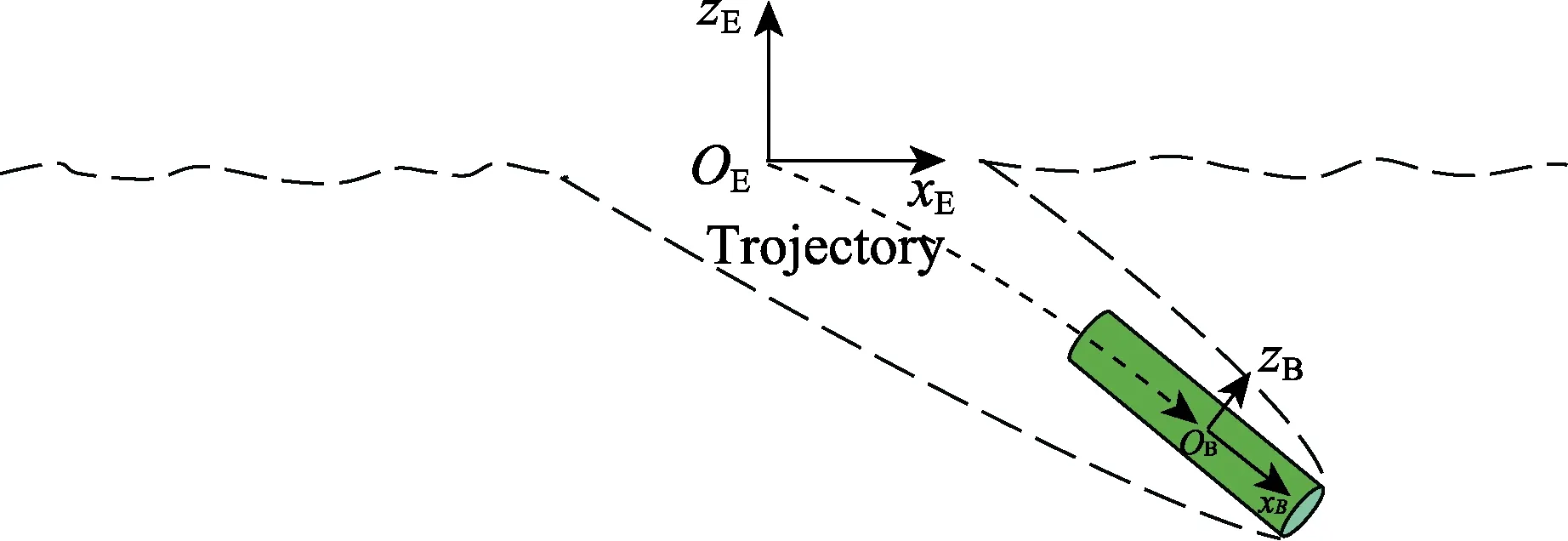
图1 坐标系Fig.1 Coordinate system
基于牛顿第二定理,建立回转体3-DOF运动方程组:
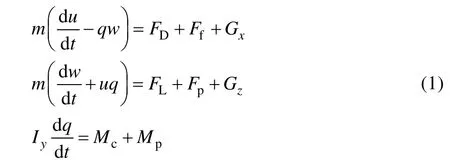
式中:为回转体的质量;I为回转体的转动惯量;和为回转体质心速度在弹体坐标系中的分量;为回转体在平面的转动角速度;G和G为回转体重力在弹体坐标系中的分量;和为回转体头部流体动力在弹体坐标系中的分量;和为回转体尾部沾湿部分的流体摩擦力和滑行力;为回转体头部流体动力对回转体质心的合力矩;为回转体尾部流体动力对回转体质心的合力矩。
1.2 入水空泡几何预报方法
如图2所示,回转体高速入水后,空泡的半径可由式(2)计算。

图2 定常超空泡Fig.2 Steady Supercavitation
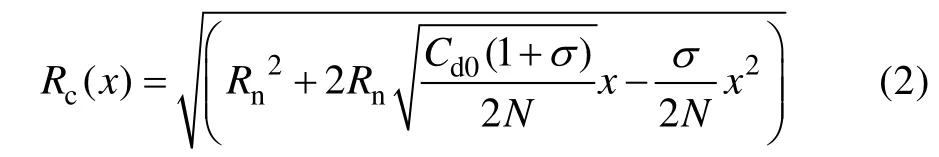
式中:为空化器中心点沿空泡对称轴线的距离;为空泡半径;为回转体头部圆截面半径;为经验系数,取为1.4;为圆盘空化器空化数为0时的阻力系数,取为0.83;为空化数,其定义见式(3)。

式中:为来流速度;为水的密度,取1 000 kg/m;=+(其中为标准大气压,取101 325 Pa,为重力加速度,取9.8 m/s,为回转体头部空化器的水深);为空泡内部压力,考虑空泡内主要为蒸汽相,可近似为水的饱和蒸汽压,水在20 ℃时的饱和蒸汽压为2 350 Pa。

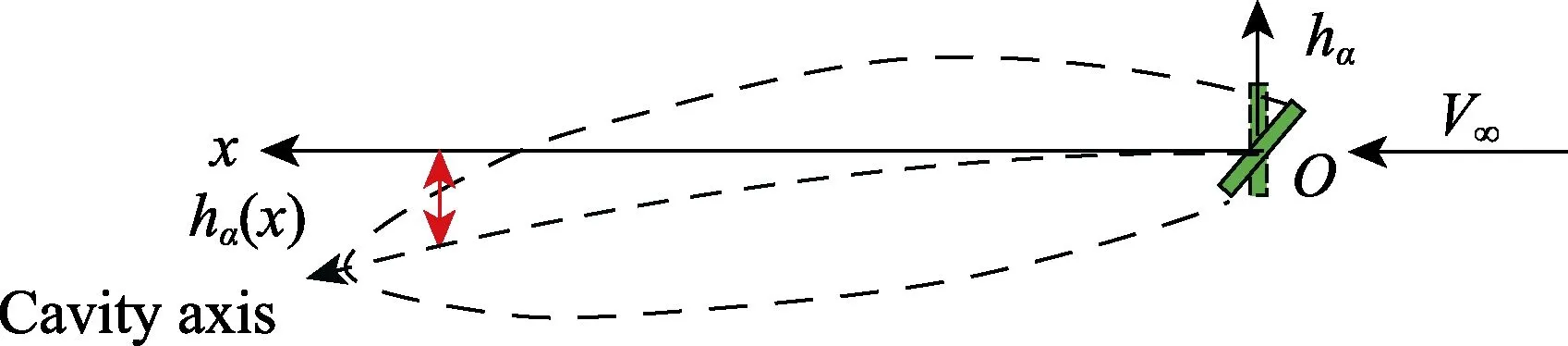
图3 空泡轴线变形Fig.3 Deformation of cavitation axis
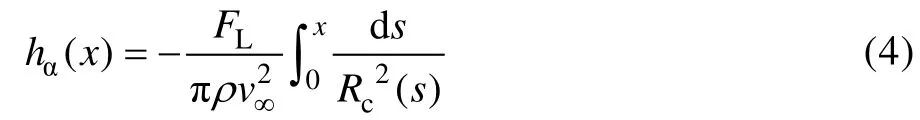
式中:为空泡对称轴线的变形高度;为空化器升力分量;为空泡半径。
如图4所示,回转体入水后,根据空泡截面独立扩张原理,空泡的每一个固定截面都相对于空化物体中心运动轨迹按相同的规律扩张,扩张规律则与空化物体通过该截面所在平面时刻的空化数、速度等状态有关。这种空泡外形不由当前时刻运动参数决定的特点就像是空泡对过去有记忆功能一样,称为空泡记忆效应。任意空泡截面的半径和相对空泡中心轴线的变形高度可由式(5)、(6)计算:

图4 入水空泡截面Fig.4 Section of water inlet cavitation
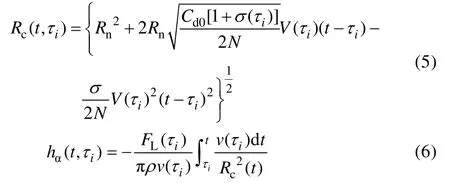
式中:τ为第个空泡截面形成的时刻;为回转体入水后的航行时间;(,τ)和(,τ)为第个空泡截面在时刻的空泡半径和相对空泡中心轴线的变形高度;(τ)和(τ)为回转体τ时刻的质心速度和空化数;()为τ时刻回转体空化器受到升力。
入水空泡的整个变化过程可以看成是空泡的各个截面按照一定规律的独立扩张过程。在纵平面内,空泡的外形可由各个空泡截面的上下顶点确定。在地面坐标系下,纵平面内每个空泡截面的顶点坐标可由式(7)、(8)计算。
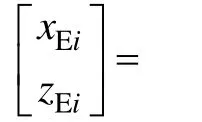

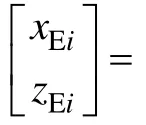
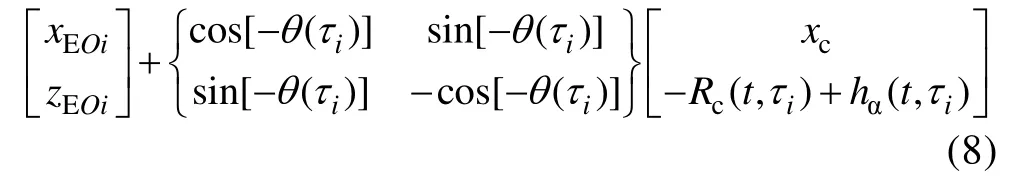
式中:和为空泡顶点在地面坐标系下的坐标;和为回转体质点在地面坐标系下的坐标;(τ)为回转体τ时刻回转体的俯仰角;为回转体头部到重心位置的距离。
1.3 受力求解
如图5所示,高速入水后回转体头部可视为圆盘空化器,流体动力可由式(9)计算。
图5 空化器流体动力Fig.5 Fluid dynamics of cavitator


回转体尾部沾湿部分流体动力由2部分组成,分别为流体摩擦力和滑行力。可通过切片法计算回转体尾部沾湿部分流体动力,如图6所示。

图6 受力分析Fig.6 Stress analysis
如图7所示,将地面坐标系下的空泡坐标转化为弹体坐标系下的坐标。在弹体坐标系下,将回转体均等切片为有限个截面,从尾部开始编号,依次计算每个回转体截面侵入空泡壁面的沾湿深度,其中尾部第1个截面作为回转体的沾湿深度。当沾湿深度为0时,计算该回转体截面与回转体尾部截面的距离,作为回转体的沾湿长度,回转体沾湿面积近似为扇形,可通过扇形面积公式计算。回转体尾部滑行升力可由式(10)计算。
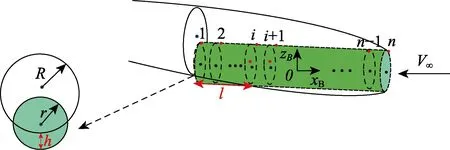
图7 回转体沾湿部分Fig.7 Wetted part of body of revolution

式中:为回转体尾部半径;Δ=-;为回转体尾部空泡半径;=-+(-)+,其中为回转体长度,为空泡横向速度;为尾部空泡收缩速度,收缩为正。
回转体尾部摩擦力可由式(11)计算。

式中:雷诺数=/,为水的动力黏度,20 ℃时,水的动力黏度为1.01×10Pa·s;沾湿面积可由式(12)计算。

回转体尾部合力矩为:

回转体质心重力在弹体坐标系中的分量G和G为:

1.4 验证算例
在回转体高速入水问题研究中,高速垂直和倾斜入水是两大主要的研究方向。通过本文建立的弹道模型编写程序,分别对文献[23]中高速垂直入水试验工况和文献[24]中高速倾斜入水试验工况进行计算模拟,以验证本文所建立的回转体高速入水弹道模型的可靠性及适用性。2种工况采用实心均质回转体结构,尺寸如图8所示,具体工况见表1。
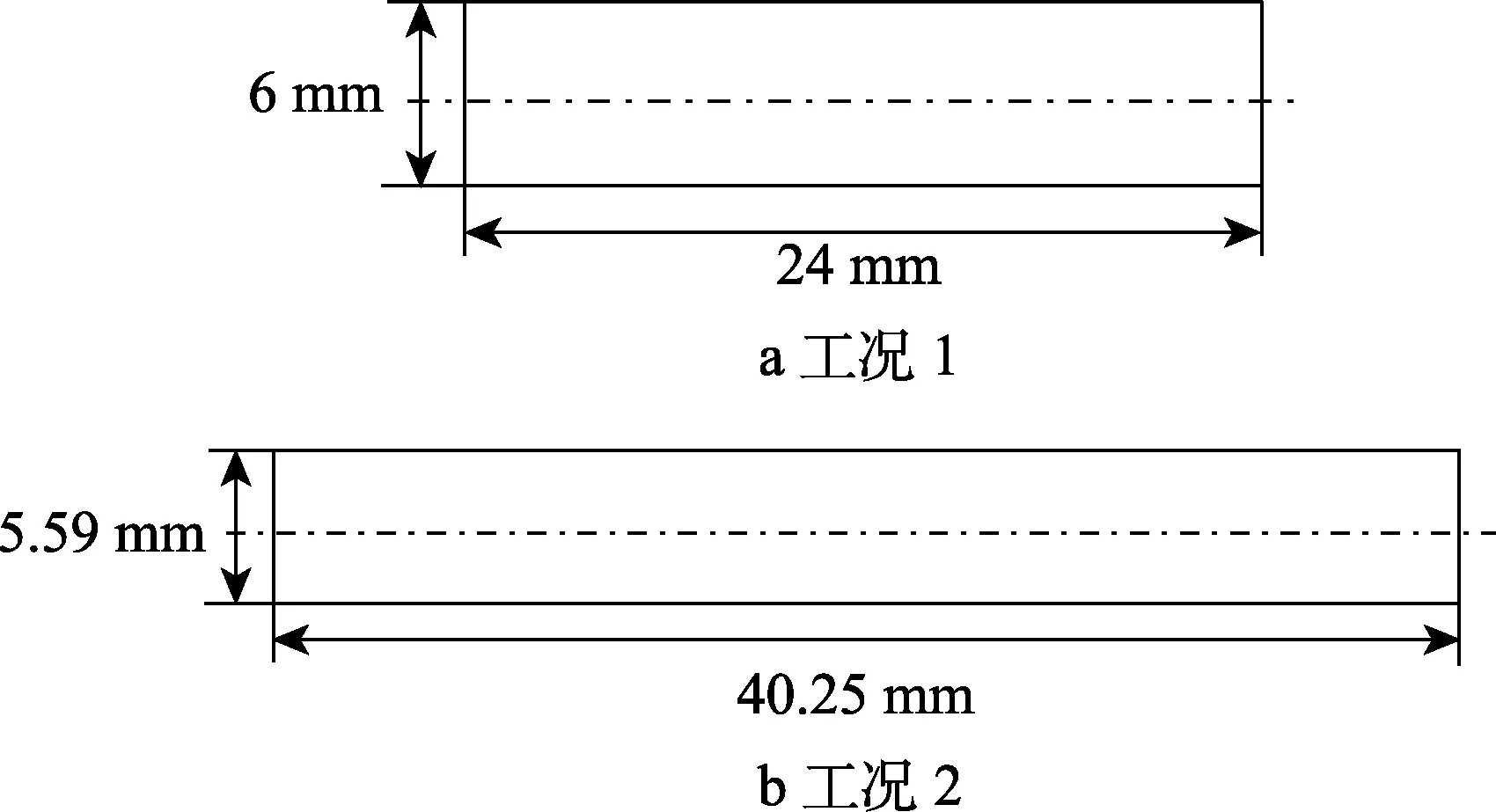
图8 回转体结构尺寸Fig.8 Structural dimensions of body of revolution:a) condition 1; b) condition 2

表1 回转体入水工况Tab.1 Working conditions of body of revolution water entry
2 结果及分析
2.1 高速垂直入水
通过本文建立的弹道模型对工况1进行计算,得到了该工况下回转体的入水空泡变化形态、质心速度和位移变化曲线,并与文献试验结果比较,以验证本文弹道模型对回转体高速垂直入水预报的有效性。
从图9可以看到,入水初期,由于回转体高速撞击水面,以入水点为中心的自由液面上方会形成冠状喷溅薄膜,同时回转体侵入水面以下,形成入水空泡。这个过程中,由于流体的黏性作用,回转体会将空气带入空泡内,并形成涌进空泡内的气流,使得冠状喷溅薄膜的内侧气流速度大于外侧。根据伯努利原理,喷溅薄膜的内侧压强小于外侧,使得喷溅薄膜逐渐由冠状收缩为圆锥状。随后发生表面闭合,液面收缩形成向上和向下2个方向的射流。此时,空泡完全与外界空气隔绝,空泡内部是空气和水蒸气的混合物。闭合后的空泡形态沿弹道轨迹对称,尾部闭合空泡横截面位置不断下降,但空泡长度逐渐增大。
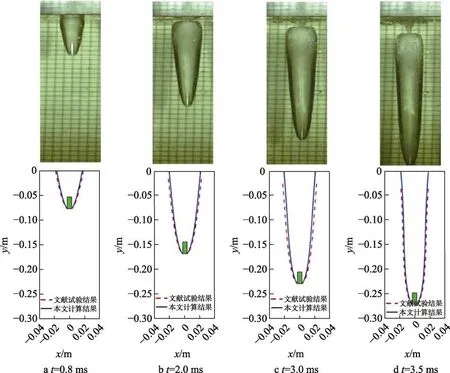
图9 工况1入水空泡Fig.9 Water inlet cavitation under working condition 1
回转体高速垂直入水时速度、位移、阻力和阻力系数变化对比如图10所示。由图10a、b可以看出,回转体质心速度变化和位移变化计算结果与试验结果保持一致,最大相对误差为2.1%。回转体在垂直入水过程中的速度在不断衰减,衰减变化由快到慢,而入水射程则不断增大。这是由于回转体高速垂直入水后,头部空化器受到阻力作用,回转体质心速度开始衰减。由于阻力与速度的平方成正比,初入水时刻回转体质心速度高,阻力较大,使得回转体质心速度的衰减相对较快。随着回转体质心速度的不断衰减,阻力也在快速减小,使得回转体质心速度的衰减速率在不断降低。在整个过程中,回转体的侵入深度在不断增大。
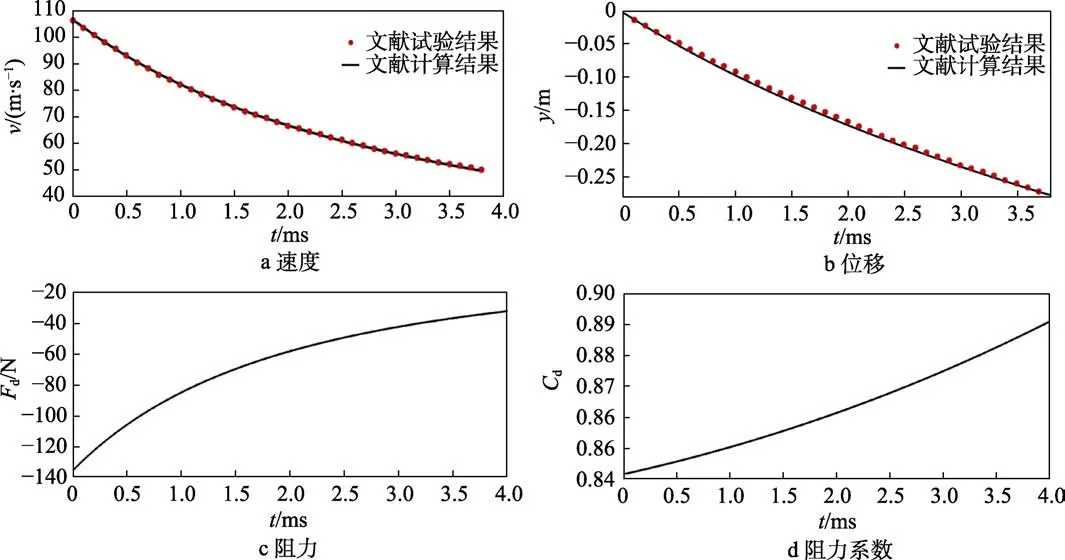
图10 回转体高速垂直入水时速度、位移、阻力和阻力系数变化对比Fig.10 Comparison diagram of variation of vertical water entry velocity (a), displacement (b), resistance (c) and resistance coefficient (d) of body of revolution at high speed
由图10c可知,回转体高速垂直入水过程中的阻力变化与上述分析相符。从图10d可见,虽然回转体在入水过程中的阻力值是在不断减小,但阻力系数却在不断增大。这是由于回转体的速度在不断衰减,使得空化数在不断增大,而阻力系数是有关空化数的弱函数,随着空化数的增大而增大。
2.2 高速倾斜入水
通过本文建立的理论模型对工况2进行计算,得到了该工况下回转体的入水空泡变化形态和位移变化曲线,并与文献[24]试验结果进行比较,以验证该理论模型对回转体高速倾斜入水计算的有效性。
高速倾斜入水初期,回转体撞击水面,头部空化器受力并不均衡。回转体头部下缘位置先受到流体动力作用,然后在极短的时间内头部表面逐渐沾湿受力。这个过程会产生力矩,导致回转体入水角度、姿态角和回转体俯仰角速度发生微小变化。在空化器完全沾湿后,回转体上侧液面会产生喷溅,是由于回转体高速倾斜入水和高速垂直入水有很大差别。回转体垂直入水后,能量主要沿径向传递,形成空泡,同时会受到侧向水压的约束,空泡动能转化为势能,致使之后空泡沿径向收缩,水面会形成表面闭合。回转体倾斜入水时,回转体撞击水面,将能量沿径向传递,但水面与射弹方向存在夹角,回转体下侧水面沿径向空泡扩张,上侧由于无侧向水压的约束,会形成液面喷溅,无法形成表面闭合。回转体倾斜入水过程中,回转体姿态角、攻角会发生变化,弹道也会发生逐渐弯曲,会使空泡上下表面的曲率不一致。与试验的空泡变化形态进行对比可知,模型计算的空泡形态下表面与试验一致,上表面与试验有较小差异,如图11所示。

图11 工况2入水空泡Fig.11 Water inlet cavitation under condition 2
回转体高速倾斜入水地面坐标系方向和方向的位移的计算结果如图12所示。计算结果与试验结果接近一致,最大相对误差为4.7%。通过计算结果可以发现,回转体在倾斜入水过程中,方向和方向的运动距离在不断增加。
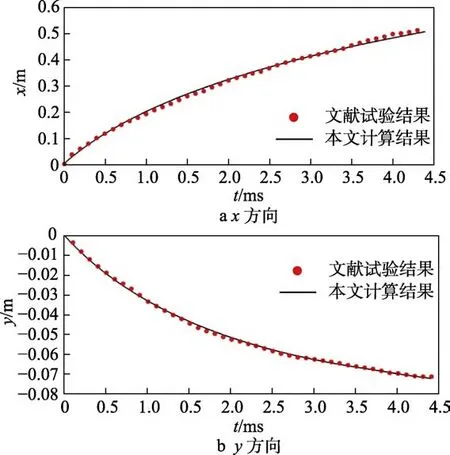
图12 回转体高速倾斜入水位移曲线Fig.12 Displacement curve of body of revolution inclined into water at high speed: a) x direction; b) y direction
从图13a可以看出,回转体速度分量v在不断减小,v变化曲线较为光滑。由图13b可知,回转体速度分量v的速也在不断减小,在3.5 ms前的变化曲线比较光滑,但在3.5 ms后,速率出现变化,v出现局部增大,后又减小,使得变化曲线出现曲折。通过图11可知,v出现局部变化主要是由于回转体侵入空泡壁面,回转体尾部受到了滑行力的升力效果作用。

图13 回转体高速倾斜入水的速率变化Fig.13 High speed inclined water entry of body of revolution variation diagram
从图14可以看出,回转体在倾斜入水后,回转体的攻角在不断减小,但在3.5 ms后,攻角的发展趋势由减小转变为上升。结合图11可知,造成攻角变化趋势改变的主要原因也是回转体侵入了空泡壁面,回转体尾部受到了滑行力的升力效果作用。

图14 回转体高速倾斜入水攻角变化Fig.14 Variation of angle of attack of body of revolution inclined into water at high speed
回转体倾斜入水俯仰角和角速度变化如图15所示。在3.7 ms之前,回转体的俯仰角速度并未发生变化,回转体的俯仰角度呈线性递减。这是由于在回转体倾斜入水初期,回转体被空泡包裹在内,并在空泡内部转动,但回转体尾部并未侵入空泡壁面,因此回转体绕质心转动的运动状态并未改变。在3.7 ms之后,回转体的转动角速率先快速减小,在减小到0时,回转体的转动方向发生转变,转动角速率又快速增大。回转体的俯仰角度先快速减小到最小值,然后又快速增大。这是由于随着回转体的转动,之后回转体的俯仰角不断减小,回转体尾部和空泡的间距在不断减小,直到回转体尾部与空泡壁面接触,回转体尾部会受到流体动力,阻碍回转体的转动,使回转体的转动角速率开始减小。随着回转体尾部侵入空泡壁面深度的增加,回转体转动的动能会被消耗,当回转体达到最大侵入深度时,回转体俯仰角将会达到临界点。随后回转体尾部沾湿部分受到径向的滑行力作用,将回转体沿相反的转动方向快速推出空泡壁面。
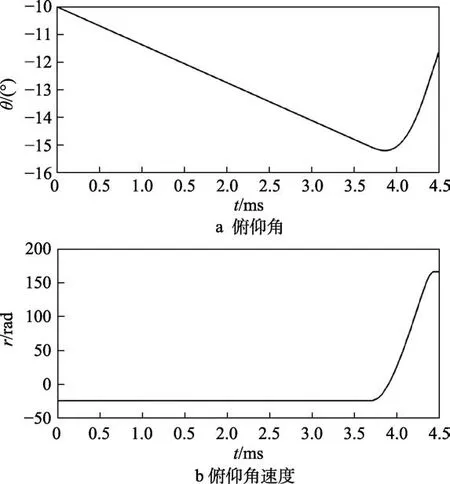
图15 回转体倾斜入水俯仰角和角速度的变化Fig.15 Variation diagram of pitching and elevation angle(a) and angular velocity (v) of body of revolution inclined into water
回转体高速倾斜入水的阻力、滑行力和流体摩擦力的变化如图16所示。回转体高速倾斜入水过程中,阻力值在不断减小,虽然在运动过程中有攻角的变化,但变化幅度较小,对阻力的影响可忽略不计,与高速垂直入水过程中的空化器流体阻力变化形式相同。回转体尾部在未侵入空泡壁面时,回转体尾部的滑行力和流体摩擦力都为0,在回转体侵入空泡壁面的过程中,回转体尾部的滑行力和流体摩擦力的先增大、后减小。
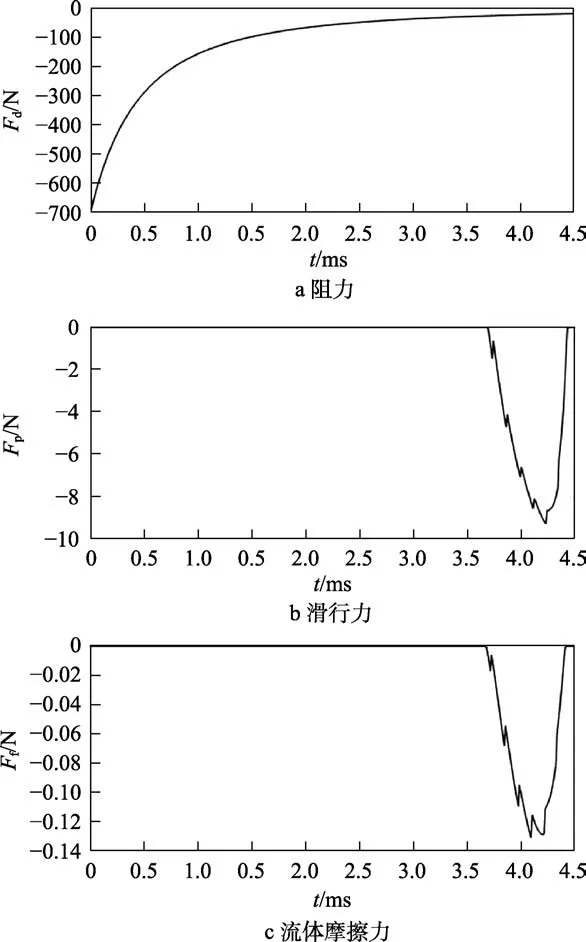
图16 回转体高速倾斜入水过程中阻力、滑行力、流体摩擦力的变化Fig.16 Variation diagram of water inflow resistance (a), sliding force (b) and fluid friction (c) of body of revolution inclined at high speed
通过以上内容可以发现,在回转体高速倾斜入水运动未失稳的情况下,回转体尾部的流体摩擦力要远小于回转体阻力,回转体的阻力主要是由空化器部分的流体阻力提供,这与回转体高速垂直入水时的阻力变化规律相同。滑行力能够为回转体在发生尾拍运动时,提供保持运动稳定的恢复力矩,防止回转体在运动过程中俯仰角和攻角变化过大。
3 结论
本文利用空泡截面扩张原理,考虑空泡记忆效应,建立了一种回转体高速入水弹道预测模型。分别对回转体高速垂直入水和高速倾斜入水过程中的空泡特性、流体动力特性和弹道特性进行分析,得到了以下结论:
1)回转体高速垂直入水,空泡形态沿弹道轨迹对称,液体表面区域会发生闭合;回转体高速斜入水,空泡上下表面曲率不一致,并不沿着弹道轨迹对称,射弹上侧液面会发生喷溅。
2)回转体高速垂直入水和高速倾斜入水时的头部阻力变化规律相同,与速度的平方成正比,对回转体质心速度衰减起主要影响。回转体高速倾斜入水过程中,尾拍运动产生的滑行力有助于回转体保持运动稳定。
3)通过与文献试验结果进行对比,模型的预测误差在10%以内,满足工程应用需求,验证了本文回转体高速入水弹道模型的准确性。

