航行体跨音速斜射入水流动特性数值模拟研究
郝亮,刘涛涛,2,黄彪,2,王国玉,2
(1.北京理工大学 机械与车辆学院,北京 100081;2.北京理工大学 重庆创新中心,重庆 401120)
航行体入水流动特性及弹道特性等问题的研究一直是国内外在发展相关装备研制过程中的焦点。其入水过程涉及到介质突变、湍动、相变等大量复杂流动,具有强瞬时性和非定常运动特性,是物体从空中弹道过渡到水下弹道的一个重要环节。入水过程包含的非定常流体力学问题,涉及到激波、自由液面和超空泡相互作用,还有跨音速跨介质运动造成的结构动态响应力学问题,对入水过程弹道稳定性和超空泡射弹结构具有很大的影响。入水过程是整个航行过程中流动现象和载荷最复杂、航行体姿态和弹道最不确定的非受控阶段,尤其入水初期,介质突变、空泡演变过程和弹道特性的研究尤为重要。
Lundstrom对穿甲弹以跨音速800~1070 m/s入水过程开展了试验研究,分析了入水空泡发展、溃灭的规律,并基于能量守恒推导出空泡预测半径的公式。之后,Hrubes对超空泡射弹开展了以亚音速、跨音速以及超音速入水试验,获得了射弹在水中航行时空泡的形态,以及超音速航行时的水中激波现象。Owis等开发了一种基于Navier-Stokes方程求解可压缩流动的数值计算方法,通过对绕半球体和圆锥体的空化流动进行数值模拟计算,验证了数值方法的可行性。Gekle等对圆盘匀速垂直入水过程进行了试验和数值模拟研究,针对伴随空泡深闭合产生的跨音速射流形成过程建立了数学模型,数值模拟计算结果与试验结果取得了较好的一致性。Jiang等采用有限体积法对水平放置的圆柱体入水过程进行了数值模拟,研究了湍流减阻添加剂在自然超空泡流过程中的作用,结果表明,当加入减阻添加剂时,空泡的长度和直径大于在水中的尺寸。叶取源基于非线性自由面理论,采用了欧拉–拉格朗日混合边界元方法对锥头和圆盘平头物体垂直入水过程进行了数值计算,分析了Froude数等因素对入水空泡发展的影响。李达钦等对绕跨音速射弹可压缩超空泡流动进行了数值模拟,研究了马赫数对超空泡流动特性的影响,推导了激波前后流动参数的表达式,同时分析了冲击波上压力与密度之间的关系。
早期航行体入水弹道研究主要针对二战中鱼雷失灵等问题,具有很强的军事应用背景。1945年,Mason和Slichter开始了对空中发射导弹后入水的现象的研究。May等对不同材料的球体进行了垂直入水的试验,分析了不同密度入水时的附加质量力。Waugh等在《水弹道学模拟》中总结了水弹道学入水试验方法和研究现状。当射弹以跨音速倾斜入水时,弹体更容易由于不稳定性而失稳。跨音速弹道倾斜入水的研究对于实现水下精确打击具有重要研究意义。Truscott对特定射弹斜射入水过程进行了试验研究,记录了射弹以0.3~1.0马赫数的入水速度,在入水角度为5°~15°系列工况下的入水空泡形态演变过程及弹道特征。当射弹跨音速入水时,流体的可压缩性对入水冲击载荷造成了很大影响。Eroshin等考虑了冲击过程中流体的可压缩性,研究表明,考虑可压缩性的入水冲击载荷偏低。
由于跨音速入水试验难度大,得到的观测数据有限,不少学者通过理论和数值计算方法研究了跨音速入水过程。随着计算流体力学的发展,基于N-S方程求解的计算模型结合动态网格技术的数值模拟方法,可以考虑湍流特性对空穴形成和发展的影响,并可以实现非定常流动、多自由度水弹道的计算,数值计算逐渐成为研究入水问题的重要方法。何春涛以RAMICS为研究对象,对超空泡形态和阻力系数进行了数值模拟研究,分析了弹身母线形状、弹身长细比以及空化器直径对空泡形态和阻力的影响,并且对带和不带尾翼的超空泡射弹进行了三维数值模拟,分析了尾翼穿透现象及其对超空泡稳定和阻力的影响。秦阳等对截锥头弹体以500 m/s跨音速斜射入水过程进行了数值模拟研究,结果表明,入水角度越大,压力峰值越高。从国内外的研究现状来看,对于入水过程的研究主要集中在低速垂直入水,对于跨音速尤其是跨音速斜射入水的研究较少。
本文基于数值计算方法,对跨音速多自由度入水展开分析,主要研究了倾斜入水过程的可压缩流体动力特性与弹道特性,讨论了入水攻角对跨音速入水过程空泡形态、流场结构以及弹道特性的影响。
1 数值计算方法
1.1 基本控制方程
本文采用VOF均相流模型对航行体跨音速入水过程多相流动进行求解。在整个计算域内,VOF多相流模型通过对互不相溶的流体求解同一个动量方程组,并追踪每种流体的体积分数来模拟多相流。VOF模型对引入模型的每一相,引入一个称为单元相体积分数的变量,在每个控制容积中,所有相的体积分数之和为1,混合介质的连续方程和动量方程见式(1)、(2)。
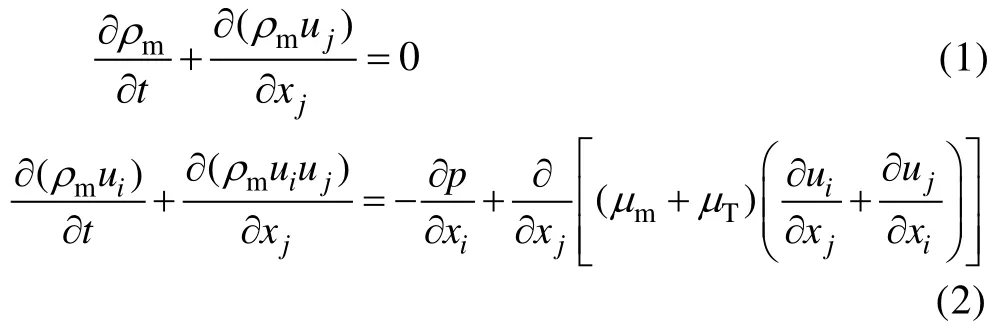
式中:和分别为混合介质的黏度和密度;、(=1,2,3;=1,2,3)表示3个正交坐标方向。
1.2 湍流模型
本文采用SST-湍流模型来封闭RANS方程。Menter提出的SST-模型,在近壁面利用-模型,在远壁面利用-模型求解,并且考虑到了湍流剪切应力的传输,得到了壁面分离流动问题的精确预测。湍流动能和湍流频率输运方程见式(3)、(4)。

式中:Г、Г为湍流扩散系数;G、G为湍流生成项;Y、Y为湍流动能耗散项;S、S为自定义项;G为交叉扩散项;为基于平均体积分数的密度;(= 1,2,3)表示3个正交坐标方向。
1.3 空化模型
Zwart空化模型结合了泡间两相流动理论,认为空穴的内外为连续体,将空穴看作一种密度发生剧烈变化的可压缩黏性流体,很大程度上考虑了空化生长以及溃灭时空泡体积变化的影响,其适用于模拟空化的非定常流动过程。在该模型中,单位体积内的相间传输速率为:


式中:为汽核体积分数;为汽泡半径;为汽化压强;和分别是蒸发和凝结经验系数。在计算中,=5×10,=1×10m,=50,=0.01。
1.4 液相可压缩性修正
水的弹性模量为2.2 GPa,一般情况下可以忽略其可压缩性,但当弹体航行速度达到跨音速或者超音速阶段时,需要考虑水的可压缩性。介质的可压缩性对射弹空泡形态和流体动力均有显著影响,在强可压缩环境下,基于常规计算无法捕捉密度和温度随压力场动态变化的过程。为了解析上述复杂耦合问题,在N-S方程的计算框架内,必须加入能量方程,其本质为热力学第一定律,见式(7)。
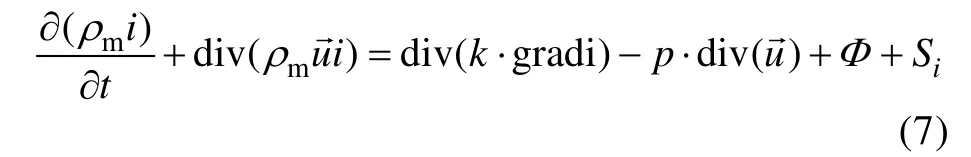
式中:为内能,=(为比热容,为温度);为流体的传热系统;S为热源项。
本文数值计算选择Tait方程作为可压缩流体的状态方程,忽略温度影响的可压缩液相水的Tait方程见式(8)。

其中,和是可以通过假设体积模量是压力的线性函数确定的系数,其值基于参考状态压力、密度和体积模量求得。
Tait方程的简化形式可以写成:

式中:为参考压力,取101 325 Pa;为参考压力下的密度,取998.2 kg/m;为参考压力下的体积弹性模量,取2.2 GPa;为密度指数,取7.15;为液体压强;分别为压力下的密度和体积弹性模量。
1.5 边界条件设置与网格划分
本文计算采用的航行体模型如图1所示,为航行体圆柱段长度,为航行体头部长度,为航行体直径。航行体总长度为240 mm,其中=20 mm,=220 mm,L=20 mm。

图1 航行体模型Fig.1 Model of vehicle
对于航行体斜射入水过程,本文只考虑纵向平面的运动,即、方向的位移和方向的偏转3个自由度。计算域三维示意图及边界条件设置如图2所示。航行体头部距水面的高度为1.25,计算域高度为100,长度为100,宽度为25。航行体表面和Wall设置为无滑移固壁,上下边界设置为压力出口,并且以弹体头部刚触及水面为0时刻。文中采用混合密度网格进行网格划分,航行体附近网格采用非结构网格局部加密,全局采用六面体结构网格。全局网格和局部加密网格如图3所示。为了减少网格,节省计算时间,航行体采用半模,航行体切面与流域前面设置为Symmetry,以减少网格数量。
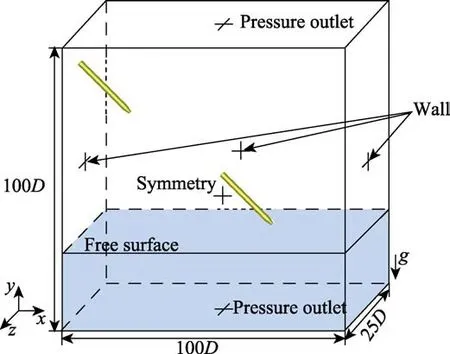
图2 计算模型Fig.2 Calculation model

图3 网格划分Fig.3 Schematic diagram of meshing
采用上文建立的数值计算方法进行模拟,选取入水角度为45°工况。计算采用基于压力的求解器,采用压力–速度耦合,利用SIMPLEC求解策略,利用二阶迎风格式求解密度与动量项,利用一阶迎风格式求解湍动能与湍动能耗散率,利用一阶隐式方程进行瞬态求解。除此之外,数值计算方法基于有限体积法,网格质量和数量对计算方法影响很大,但网格数量过大会影响计算效率,因此在保证计算精度的情况下要尽量减少网格数量。对航行体周围网格以及加密区域边界节点进行加密,建立3种不同网格密度的网格,网格数量分别为160万、400万、600万。3种网格下的阻力系数变化如图4所示。由图4可知,网格为160万时,阻力系数峰值和稳定后的阻力系数偏低,随着网格加密,阻力系数变化趋于一致。为了节省计算时间,选用400万网格密度进行后续计算分析。

图4 不同网格数量下阻力系数变化曲线Fig.4 Variation curves of resistance coefficients under different grid numbers
1.6 数值计算方法验证
为了验证数值计算方法的准确性和可行性,对比了利用上述数值计算方法的计算结果与魏卓慧和Hurbes的试验结果。入水角度=45°斜射入水过程中,航行体速度和弹道轨迹随时间变化的试验结果和数值结果对比如图5所示,其中航行体运动轨迹以航行体质心位置表示。由图5a可知,在入水过程中,随着入水深度的增加,速度不断降低,入水速度数值计算结果和试验结果吻合较好。由图5b可知,数值计算结果弹道轨迹与试验结果基本吻合。综上所述,数值计算结果与试验结果取得了良好的一致性。

图5 数值计算结果与试验结果对比Fig.5 Comparison between numerical results and experimental results: a) speed; b) projectile displacement
为进一步验证数值计算方法对跨音速水中激波现象的模拟,图6给出了=1.03(1540 m/s)下数值计算结果与Hurbes的试验图像结果。从数值计算结果的压力云图可以看出,射弹头部出现的高压现象与试验结果一致,形成了弓状激波,并且激波面与试验中捕捉到的激波面基本吻合,充分验证了数值计算方法的准确性与可行性。
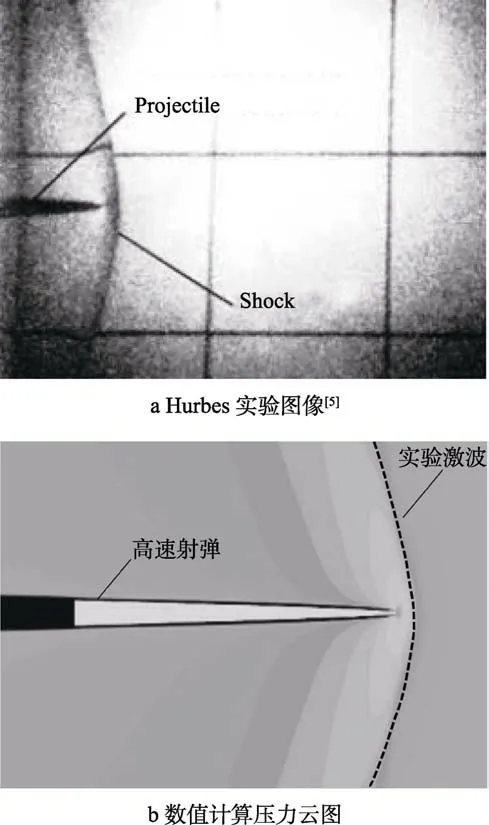
图6 Ma=1.03时射弹超空化试验图像与数值计算结果对比Fig.6 Comparison between projectile supercavity test image(a) and numerical results (b) when Ma=1.03
2 结果及分析
2.1 液相可压缩性对入水流动特性的影响
本文模拟计算了不同时刻下航行体参考线位置的压力分布,参考线如图1所示。当入水角度为45°,入水速度为1 500 m/s时,其压力分布如图7所示。由图7可知,在0.025 ms时,航行体周围压力分布具有很强的不对称性,迎流面侧航行体附近压力最大值明显低于背流面。随着入水深度的增加,这种不对称性逐渐降低,航行体两侧压力分布趋于一致。对于不可压缩工况,航行体两侧压力最大值随入水时间的增加而增大,并且在初始时期迎流面侧压力增长明显,背流面侧压力影响范围基本不变,而迎流面压力分布范围增加。在可压缩流场中,背流面侧压力最大值先减小、后增大,而迎流面侧压力最大值迅速增大后缓慢增加,并且压力分布沿径向方向迅速增加后出现陡降现象。航行体两侧最大压力差值较为明显,并且随着入水深度的增加,由于航行体速度衰减,激波角增大,激波强度减弱,压力发生陡降的转折点逐渐远离航行体,陡降趋势减弱。

图7 航行体附近压力分布Fig.7 Pressure distribution near the vehicle: a) incompressible condition; b) compressible condition
不考虑和考虑可压缩性下,入水过程中空气相与蒸汽相云图见图8,其中黑色实线为空泡轮廓。由于计算深度有限,仅能观察到航行体带空泡航行阶段,入水空泡始终与大气相连。可以看出,入水空泡由空气相和蒸汽相构成。在入水初期,背流面侧空泡几乎全由蒸汽相构成,空气相主要从迎流面侧灌入。随着入水深度的增加,蒸汽相不断增加,并且分布区域紧邻两侧空泡壁面,航行体两侧存在的空气不断减少。对比不考虑和考虑可压缩性工况可以看出,两者水汽分布不同主要体现在迎流面。可压缩工况下,空泡内部的空气相明显多于不考虑可压缩工况(如6.5 μs时刻),迎流面蒸汽相仅沿空泡壁面存在。不考虑可压缩性时,蒸汽相存在范围宽度更大。

图8 不同入水时刻空气相和水蒸气相分布云图Fig.8 Cloud diagram of air phase and water vapor phase distribution at different water entry times:a) incompressible condition; b) compressible condition
2.2 入水攻角对入水流动特性的影响
本小节主要讨论入水攻角对跨音速入水过程流体动力特性和弹道特性的影响。入水速度为1 500 m/s,入水角度为45°,入水攻角分别为:–3°、–1°、0°、1°、3°。相同入水深度下,不同攻角的空泡轮廓以及对应时刻的水相分布云图见图9。可以看出,不同攻角下,空泡轮廓存在很强的相似性;在相同入水深度下,空泡直径趋近一致,背流面空泡长度始终大于迎流面,迎流面产生的飞溅水冠高度始终高于背流面,水冠飞溅高度也不断增长。不同攻角下,迎流面空泡直径趋于一致,水冠飞溅高度和空泡半径近乎一致,而背流面空泡轮廓存在较大差别。对于背流面空泡,在航行体头部附近,空泡直径几乎无差别,但结合水相云图可以看出,随着正负攻角的增加,航行体锥段背流面或迎流面会逐渐出现沾湿,空泡完整性遭到破坏。在自由液面附近,空泡轮廓差异较大。随着入水正攻角的增加,背流面空泡半径增加;随着负攻角增加,背流面空泡半径减小。
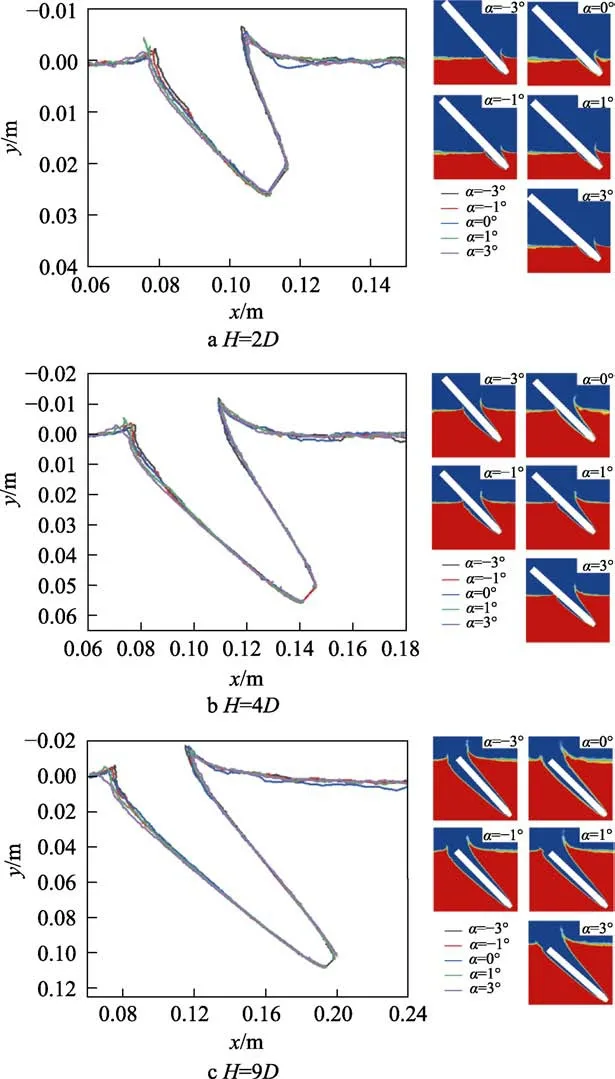
图9 不同攻角下的空泡轮廓Fig.9 Cavity profile at different angles of attack.
为了进一步研究攻角对航行体沾湿面积的影响,图10给出了航行体无量纲沾湿面积随入水时间的变化曲线。可以看出,沾湿面积变化基本可以分为3个阶段:1)在入水撞击瞬间,航行体头部以及航行体沾湿面积迅速增加,随后航行体周围开始形成入水空泡,沾湿面积迅速减小;2)由于在入水初期航行体始终与自由液面水相接触,沾湿面积不断增加;3)随着入水深度继续增加,航行体完全被空泡包裹,沾湿面积再次减小,并且趋于稳定。在阶段1)中,随着入水攻角的增大,沾湿面积峰值增大,并且随负攻角的增大而减小,随正攻角的增加先减小、后增大。这是由于正负攻角的存在改变了航行体撞击水面过程中背流面侧的沾湿面积。在阶段2)中,随着负攻角的增大,航行体沾湿面积大幅增加,并且沾湿面积增长幅度增大;随着正攻角的增加,航行体沾湿面积先减小、后增大。在阶段3)中,–1°~1°攻角下,航行体完全被空泡包裹,航行体沾湿面积趋于一致,但是由于–3°和3°攻角航行体锥段存在沾湿,在稳定阶段沾湿面积高于其他工况。

图10 不同攻角下航行体沾湿面积随时间的变化曲线Fig.10 Variation curves of wetted area of vehicle with time under different angles of attack.
不同攻角下弹体俯仰角及其角速度的变化曲线如图11所示。由图11可知,在–1°~1°攻角内,弹体俯仰角及其角速度变化呈现相同的变化规律。航行体撞击自由液面后,航行体俯仰角沿逆时针旋转,并且随着入水深度的增加而增大,角速度在入水撞击后迅速增加。在带空泡航行阶段,角速度趋于定值,俯仰角基本呈线性增加。俯仰角偏转值随负攻角的增大而增加,随正攻角增加,航行体俯仰角沿逆时针偏转值减小。由于较大攻角工况下航行体与空泡壁面有接触,造成这2个工况具有不同的变化规律。对于–3°攻角,在入水过程中,弹体锥段始终与背流面空泡接触,航行体受力不稳定性加剧,角速度随入水深度的增加而增大,俯仰角变化不再呈线性增长。同理,3°攻角工况下,弹体锥段始终与迎流面空泡接触,导致弹体偏转一定角度后,开始反向偏转,角速度在入水撞击增至峰值后开始逐渐降低,最终反向增加。
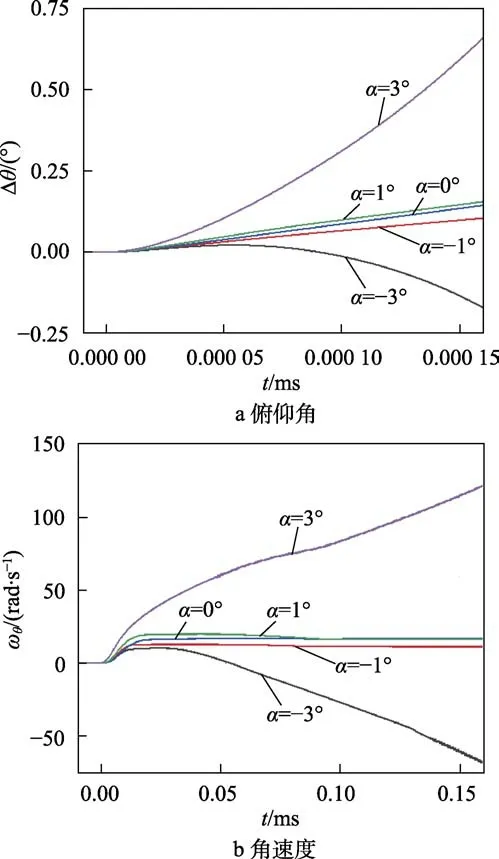
图11 不同攻角下弹体俯仰角及其角速度变化曲线Fig.11 Variation curves of pitching angles (a) and angular velocity (b) under different angles of attack
不同攻角下弹道轨迹和弹道偏移量随时间的变化曲线如图12所示。可以看出,不同攻角下,弹道轨迹接近直线。在入水初期,弹道均向上发生偏移,随着入水深度的增加,弹道偏移量出现不同的变化规律。当入水攻角为–1°~1°时,弹道轨迹偏移量随着入水深度逐渐增大,基本呈线性增长;在攻角为3°时,弹道轨迹偏移量随入水深度的增加而急剧增加,弹道偏移量远高于其他工况;当入水攻角为–3°时,弹道轨迹在入水初期由向右侧偏移逐渐变换,甚至发生反向偏转,弹道逐渐向左侧偏移,且偏转量增长速度逐渐加快。整体来看,随着正攻角的增大,弹道轨迹正向偏转量急剧增加;随着负攻角增加,弹道偏移量先略有增加,随后弹道偏移发生负向偏转。
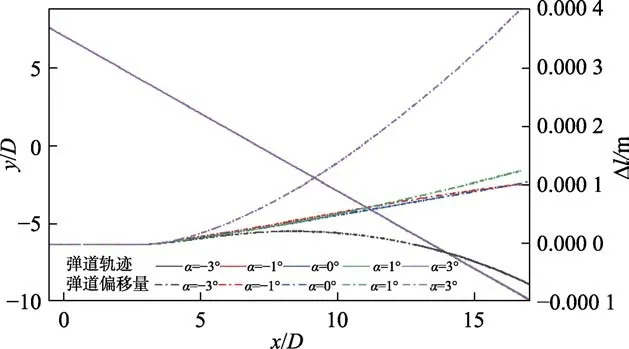
图12 不同攻角弹道轨迹和弹道偏移量曲线Fig.12 Trajectory and trajectory offset curves at different angles of attack.
不同攻角下航行体水平方向和垂直方向受力系数的变化如图13所示。由图13可知,不同入水攻角下,垂直方向受力系数的峰值均高于水平方向。随着正攻角的增加,垂直和水平方向的受力峰值减小;随着负攻角增加,垂直和水平方向的受力峰值先增大、后减小。这是因为随着正攻角的增加,在入水撞击过程中,航行体头部与水面接触面积减小,受力系数峰值降低;随负攻角的增加,虽然在入水冲击过程航行体头部与水面接触面积增加,但速度与航行体轴线夹角不断变大,法向速度减小,可能造成航行体受力降低。在带空泡航行阶段,随着入水深度的增加,航行体逐渐被入水空泡包裹,航行体受力系数迅速降低,并趋于平稳。在小幅度攻角变化范围(–1°~1°)内,稳定阶段受力系数相差很小,但随着攻角进一步增加,水平方向的受力系数随负攻角的增大而增加,随正攻角增加而减小,垂直方向受力系数变化与之相反。因为在–1°和1°攻角下,航行体在带空泡稳定航行过程中始终处于空泡包裹,但当入水攻角进一步增加,在航行体锥段将会出现沾湿,造成了垂直和水平方向受力变化。以–3°攻角为例,航行体锥段在带空泡航行阶段与迎流面始终接触,航行体受到空泡壁面的反作用力,既增加了航行体水平方向受力,也减小了垂直方向受力。
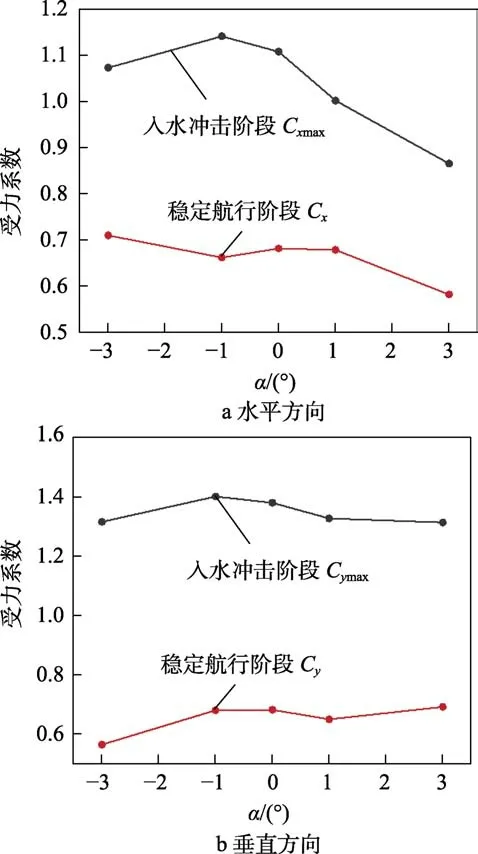
图13 不同入水攻角下水平方向和垂直方向受力系数变化Fig.13 Variation of force coefficients in horizontal direction(a) and vertical direction (b) under different angles of attack
3 结论
本文应用能量方程和水的Tait方程进行了液体可压缩修正,基于SST湍流模型、Zwart空化模型和动网格技术,建立了航行体跨音速斜射入水数值模拟计算方法。数值计算结果与试验结果对比取得了较好的一致性,验证了数值计算方法的可行性。基于该数值计算方法,研究了航行体跨音速斜射入水过程的流动特性及其弹道特征,得出如下主要结论:
1)航行体跨音速入水过程中,流体的可压缩性对航行体受力特性和流场结构有较大影响。在考虑流体可压缩性时,航行体两侧压力分布呈现出明显的不对称性,随着深度的增加,不对称性减弱,并且压力峰值先增加、后减小。除此之外,空泡内部空气明显多于不考虑可压缩工况。
2)航行体以不同攻角入水时,流场结构的发展具有相似性,但随着攻角减小,入水空泡直径略有减小。攻角为3°时,航行体沾湿面积最大,随后逐渐与–3°攻角情况相同。
3)航行体以–3°/3°攻角入水时,航行体姿态发生明显偏转,并随着入水深度的增加,弹道偏移显著变化。

