水下火炮燃气后效流场特性研究

祁晓斌，李瑞杰，范平，顾宇涛，苗圃，王瑞

（西北机电工程研究所，陕西 咸阳 712099）

随着超空泡减阻技术的发展，利用火炮发射超空泡射弹能够实现对水下威胁目标进行跨介质打击。然而，随着水下威胁目标向更深处发展，尤其是面对灵活多变的UUV，这种打击方式将会“力不从心”。通过借鉴导弹水下发射技术思想，发展火炮水下发射技术，可以有效延伸超空泡射弹水下射程，从而提升火炮的水下打击能力。然而，火炮在水下发射时，射弹出炮口后，高温高压燃气进入水中，与水掺混，形成炮口燃气泡，炮口燃气泡在膨胀‒收缩‒断裂等发展过程中，会对炮口附近流场产生较大的压力波动，而高速射弹在入水初期，微小的扰动会对空泡形态和流体动力产生不利影响。因此，研究水下火炮发射后效期流场具有重要的意义。

在水下发射流场/压力场方面，学者们进行了大量的研究工作，但主要集中在水下导弹发射方面。王汉平等针对考虑筒盖系统的水下筒口流场进行了仿真研究，获得了筒口气泡的发展特性和筒盖受载特性，提出了采用附加气室实现筒盖降载的方案。他们还开展了筒口燃气后效对水下潜射模拟弹的影响研究，发现汽水相变对发射过程影响较小，均压气体模型对燃气后效的影响较大。程用胜等采用理论建模的方法，建立了汽水耦合计算模型，分析了导弹水下发射燃气发展规律，获得了发射筒内压力和温度的分布特性。殷崇一等通过建立导弹水下发射模型，掌握了导弹在发射筒内的压力分布规律。蔺翠郎等对潜射导弹“热”发射过程的热效应进行了研究，掌握了发射筒内燃气射流的发展特性及其壁面温度分布规律。苗佩云等基于CFD方法建立了同心筒水下发射三维数值模型，获得了筒内流场分布特性。熊永亮等探究了导弹水下发射过程中发射筒内旁泄流的发展机理，结合多次试验，建立了水下发射外筒疏通的数学模型。

目前，枪炮的水下发射研究成为了热点研究课题，大都针对12.7 mm机枪为研究对象。张京辉等开展了弹道枪水下发射试验研究，同时建立数值仿真模型进行了相互验证，获得了水深对膛口流场发展演变过程与燃气射流分布特性的影响规律。张欣尉等对机枪水下发射过程进行了数值模拟，研究了机枪在空气和水中发射时的温度场特性，获得了装药参数对水下发射膛口流场分布特性的影响。张旋等开展了机枪水下密封式发射时的膛口流场，获得了发射初速对水下发射流场特性的影响规律。可以看出，前人研究主要围绕水下枪械的膛口流场、水下射流等方面展开研究，而在30 mm口径身管武器水下发射过程中的流场特性及其对高速射弹超空泡发展与形态影响的研究较少。

文中针对30 mm口径火炮水下发射超空泡射弹炮口燃气后效问题，基于CFD软件FLUENT，运用UDF和动网格技术，考虑射弹空化，建立含射弹的水下火炮发射模型，仿真计算射弹离炮口过程中燃气后效流场。获得了炮口燃气射流流场燃气泡演变形态以及压力场变化特性，同时掌握了射弹水下自然空泡的发展形态，可为火炮水下发射技术的发展提供理论基础。

1 仿真模型建立

1.1 物理模型简化

为了不失真实性地简化仿真计算，对模型作以下近似假设：

1）仅建模发射炮管和射弹的主体结构，采用二维轴对称计算流场。

2）忽略肩部空泡和发射炮管的传热损失，不考虑水汽相变，将弹尾离炮口作为计算起点时刻，此时不考虑空泡生成。

3）射弹模型为次口径弹丸。弹丸离炮口前，有卡瓣及弹带闭气，认为少量燃气进入水中对初始流场的影响较小；当弹尾离开炮口后，大量燃气涌入水中，暂不考虑脱壳对流场影响。

4）假定计算起点时刻身管内混合燃气压力、温度分布均匀，且为静止状态。管内火药燃气用理想气体代替，其参数按实际弹射气体的组分进行折算。

1.2 VOF方法及其控制方程

1）体积分数方程：

采用VOF实现气、汽、液多相之间的界面追踪。由于本文中暂不考虑相变，方程右端为0。水相为主项，燃气相和蒸汽相作为基本相。各相体积分数的计算基于式（2）的约束。

式中：下标l、g、v分别代表液相、燃气相和蒸汽相；为各相的体积分数。

2）连续方程：

式中：分别为glv；ρ表示对应项的密度；u为不同单一相的速度；为水相与汽相之间的输运量，当发生质量输运时，不为0，反之此项为0。

3）动量方程：

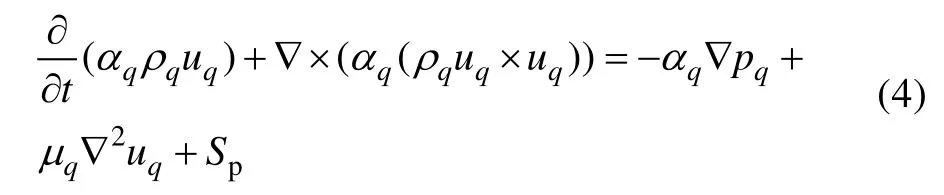
式中：p表示不同单一相的压力；表示水相与汽相发生质量输运时的动量变化，当发生质量输运时，不为0，反之，此项为0。

4）能量方程：

式中：为多相的混合密度；为混合平均能量；为混合相的压力；为混合相的平均温度；为相间的有效热传导率；为能量方程源项，其定义为空化引起的流场能量改变。

5）状态方程：

研究将燃气相作为可压缩相，水相为不可压缩相，=319.6 J/(kg·K)，为火药常数值。

1.3 网格划分

按照上述假设，建立的计算域如图1所示。

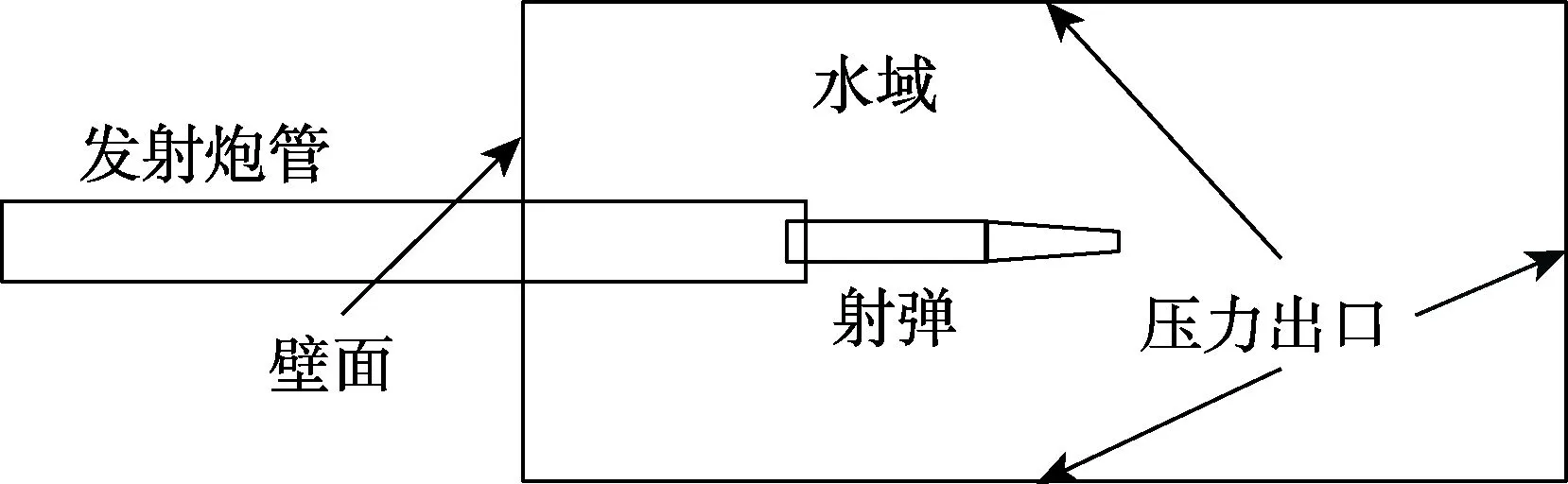
图1 计算域示意图Fig.1 Schematic diagram of the computational domain

由于模型的对称性，计算模型采取二维轴对称。对称中心取为Axis边界条件，发射炮管内壁、射弹壁面等边界条件均指定为Wall，构建外围水域，其周围边界条件取为Pressureoutlet，其压力数值按照实际所处水深指定。最终建立的网格计算域尺度为10 m×5 m，该计算域尺度能够保证流场不受壁面效应的影响。

网格划分的原则：全部流场区域采用结构化网格，网格足够细，使得计算结果不存在网格的依赖性。划分时注意水下火炮炮口附近处的网格大小接近一致，且最小尺度取为0.5 mm。外场划分梯度网格，靠近弹体位置网格细密，远场较为稀疏。按照以上要求划分网格，并进行了网格无关性验证（坐标见表2），如图2所示，最终得到全域网格如图3所示。网格量约为49万，能够保证网格具有较高的仿真精度和计算效率。

图2 压力随时间的变化规律Fig.2 Pressure characteristics vs.time

图3 炮口局部网格Fig.3 Local grid of muzzle

1.4 模型设置

1）采用RNG-模型、标准壁面函数法，Zwart-Gerber-Belamri（ZGB）空化模型。

2）压力‒速度耦合方程求解算法方式采用SIMPLEC，分离算法采用PRESTO！，动量方程、能量方程和湍流方程的离散格式均选用一阶迎风差值格式，体积分数的计算选用QUICK差值格式。

3）松弛因子压力设置为0.3，密度设置为0.4，动力设置为0.3，其他均为默认值。

4）通过fluent中层变（Layering）动网格和UDF二次开发实现射弹的水下运动。

5）初始化过程：先对全域进行初始化，此时全域为水相，然后Patch发射身管，赋予将燃气相，对局部流场参数进行修正。

6）计算步长控制在1×10s内。

2 结果及分析

本文基于30 mm身管口径，通过水下密封式发射试验测试获得的射弹离膛初始速度为500 m/s，膛压为60 MPa，膛温为2 000 K。以此作为发射初始条件，开展在1 m水深环境下的炮口后效期射弹运动过程数值模拟研究。

将射弹弹尾离开炮口定义为=0 ms时刻，此时发射炮管内完全被高温高压火药气体充满，炮口处形成明显的水气分界面，随后火药燃气推动射弹出管，该过程如图4所示。当射弹弹尾离开炮口，炮管内的火药燃气溢出，进入水环境，形成炮口燃气泡，同时亦附着于射弹尾部。在时刻，燃气泡主要沿着轴向（即射弹的运动方向）发展，此时炮口压力最大，燃气速度高于射弹运动速度，射弹受到来自燃气的推力。随着射弹的运动，压力波开始扩张，燃气泡的发展开始向径向扩张，此时燃气速度逐渐降低，射弹受到的推力逐渐降低。在时刻，燃气泡径向发展明显。此后，随着射弹的不断运动，燃气泡被拉断，炮口燃气泡呈现不断膨胀状态，直至泡内压力恢复到当地压力值。

图4 炮口燃气泡发展过程Fig.4 Development process of muzzle gas bubble

射弹运动的速度曲线如图5所示。结合图4可以看出，火炮水下发射后效期发展过程使得射弹获得了加速，期间经历短暂的速度恒定后急剧加速，在0.000 5 s时刻，速度增加到接近508 m/s，随后速度骤降。这是因为在0.001 s时刻前，泡内压力足够大，处于急剧扩张，但随着弹体与炮口的距离拉大，使得燃气泡的体积增大，最终导致产生的推力小于射弹航行阻力，速度开始衰减。

图5 射弹轴向速度曲线Fig.5 Axial motion curve of supercavitation projectile

火炮后效期发展过程中高速射弹超空泡发展过程与压力分布如图6所示，其中上半部为密度云图，下半部为蒸汽相体积分数，为射弹质心位移，为射弹弹长。可以看出，由于射弹尾部燃气泡的存在，使得自然超空泡的发展受到抑制。在/=1.2位置处，射弹尾部燃气泡还未发展颈缩，此时超空泡与燃气泡连通，高压燃气进入空泡内，抑制了自然空化的发展，使得超空泡发展受阻，空泡不能迅速闭合于弹体尾部。随着射弹的不断运动，燃气尾泡内部压力逐渐下降，燃气泡不断发展膨胀‒收缩等历程，高速射弹尾泡逐渐出现颈缩断裂迹象。在/=3位置处，自然超空泡已经发展至弹尾后，尾部交互位置的空泡底凹。随着高速射弹不断远离炮口，高速射弹与燃气泡发射断裂，该位置大致在/=1.5处。此时自然超空泡已充分发展，空泡逐步发展闭合，在/=5位置处，形成闭合空泡。

图6 燃气后效作用下的空泡发展过程与压力分布Fig.6 Cavitation development process & pressure distributions under gas aftereffect

为了考察水下发射流场的压力特性，在炮口处布置了11个不同的监测点。监测点设置思路是为了获得火炮水下过程中不同方向以及不同距离的压力特性，监测点的位置分布见图7和表2。

表2 监测点坐标位置Tab.2 Layout of monitor positions

图7 炮口监测点布置Fig.7 Layout of muzzle monitoring points

测点压力的变化曲线如图8所示。可以看出，在射弹弹尾离开炮口瞬间，燃气射流进入水中，此时炮口中心处压力幅值最大。然后压力急剧下降，在0.5 ms时刻后，出现压力脉动。在2 ms时刻内，呈现周期性脉动，脉动幅值基本维持不变，这与燃气泡的膨胀–收缩发展历程相对应。在随着燃气射流充分发展，炮口测点压力迅速上升，炮口前方测点的压力幅值要大于炮口之后测点压力。在同一射流线上，远离炮口处的压力值会迅速减小，这是因为弹尾离炮管，燃气泡膨胀，管口急剧泄压。随着压力波的扩散，冲击波逐渐减弱。在4 ms时刻后，炮口压力幅值趋于稳定。

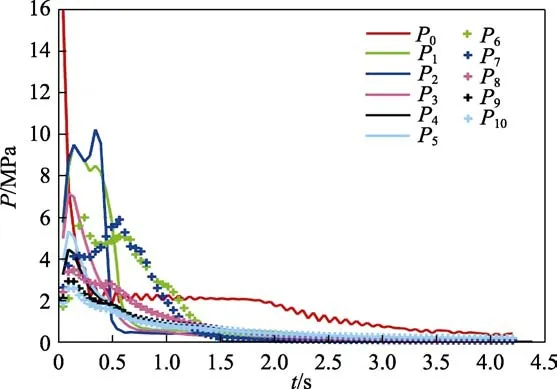
图8 测点压力随时间的变化规律Fig.8 Variation law of pressure at measuring point with time

为了验证模型的有效性，提取弹道炮水下发射高速射弹的空泡形态，通过提取空泡边界与数值计算，对超空泡进行对比。水下发射试验影像图片见图9a，超空泡射弹试验与仿真轮廓对比见图9b。可以看出，火炮水下发射过程中形成了炮口燃气泡，超空泡射弹弹道呈近直线弹道（视场中弹道线倾斜是由于拍摄角度原因），因此文中简化为二维对称模型合理有效。通过将射弹同一位置处的试验与仿真空泡轮廓进行对比，在=0.32 mm位置处的最大误差为9.31%。该结果具有较好的一致性，表明数值仿真方法的基本合理。

图9 数值模型验证Fig.9 Numerical model verification: a) photos of typical gun underwater firing; b) comparison diagram of cavitation profile between experiment and simulation

3 结论

1）水下火炮炮口燃气泡在身管内部火药气体压力、壁面边界及射弹运动的耦合影响下，发生扩张、收缩、断裂等一系列变化历程，燃气泡扩张初期能够加速射弹运动。

2）高速射弹入水后形成超空泡，燃气泡与超空泡随弹体运动发生融合，使得泡内压力升高，射弹自然空化被抑制。在高速射弹距离炮口5倍弹长后，空泡充分发展，形成闭合空泡。

3）炮口中心处压力脉动规律最为复杂，且燃气射流中心压力幅值最大。随着远离炮口中心，压力幅值减小。在4 ms时刻后，炮口附近压力降至最小。