面向高比例新能源并网场景的风光-电动车协同调度方法

风电和光伏出力具有随机性、波动性和不可控性等固有属性，高比例新能源并网给电力系统的安全稳定运行带来严峻考验.同时，随着电动汽车的大规模趋势性发展，电动汽车充电负荷需求增加，其无序充电的不确定性同样增加了电力系统调度的难度.但是，电动汽车充电负荷是具有可调度性的柔性负荷，加以引导变无序充电为有序充电能够起到平滑等效负荷波动性的目的.因此，通过风光-电动汽车协同调度能够有效降低风光出力和电动汽车无序充电等多重不确定性对电力系统的不利影响.

针对风光-电动汽车协同调度，国内外相关学者进行了相应研究.Song等提出的充放电策略考虑了电动汽车与风力发电在平抑负荷波动方面的互补效应；侯建朝等以等效负荷方差和车主支付费用最小为优化目标，构建风电与电动汽车协同调度模型；冉忠等以电动汽车消纳后的风电弃风量最小为目标，建立电动汽车参与受阻风电消纳的源荷优化控制模型；葛少云等通过遗传算法求解以峰谷差率最小为目标的优化模型；郭春林等建立了电动汽车与可再生能源双层协调优化模型，上层模型以等效负荷波动最小和可再生能源渗透率最大为双优化目标，下层模型以实现电动汽车充放电负荷跟踪为目标，并采用遗传算法求解上下层的优化模型.同时，由于风电和光伏出力具有很强的随机不确定性，在不同典型出力场景下，风电和光伏出力特性及其之间的互补关系具有明显差异性，且对电力系统的影响规律不尽相同，在含大规模新能源的电力系统中，风光出力的随机不确定性对电力系统的不利影响也愈发明显.利用典型日聚类方式从大量风电/光伏历史数据中提取典型出力场景集，以典型出力场景反映风光出力特性，并用于不同出力场景下优化调度的差异化建模分析，是目前电力系统调度分析常用的方法.

综上所述，现阶段风光-电动汽车协同调度模型多以等效负荷波动最小为优化目标，仅考虑了等效负荷的整体波动性，无法衡量风光出力与负荷的匹配度，且优化调度模型在不同出力场景下的适用性和鲁棒性也并未展开分析.

（2）流程服务层：该层是开放式流程平台的核心，将所有流程及表单的开发、运行环境统一起来，形成标准化的表单、标准化的流程图、标准化的事件响应代码，即实现流程服务的标准化和平台化。

针对上述问题，提出一种面向高比例新能源并网场景的风光-电动车协同调度方法.首先，通过分析电动汽车行驶规律，构建基于蒙特卡罗模拟的电动汽车无序充电模型；其次，基于风光出力预测数据，构建基于Gap statistic和-means++算法的风光出力典型日划分模型；再次，以等效负荷方差和负荷追踪系数最小为双优化目标，构建风光-电动汽车协同调度模型，并采用NSGA-II算法进行模型求解；最后，基于中国西北某省风光电站预测出力和电网预测负荷数据，验证所提方法的适用性和鲁棒性.

1 基于蒙特卡罗模拟的电动汽车无序充电模型

1.1 电动汽车行驶规律

电动汽车行驶规律主要包括车辆出发前往工作地点时间、返回住所时间、路程耗时和日行驶里程.2017年美国交通部对全美家庭出行调查结果反映了车辆一天中的行驶规律分布，考虑到中国与美国在工作时间上较为接近，均集中于9:00—17:00，可以假定两国电动汽车具有相同的行驶规律.因此，基于上述调查结果对电动汽车充电曲线进行建模分析，得到电动汽车出发前往工作地点时刻符合混合高斯分布，概率密度表达式为

突然，他把手按到我的腹部。他的手指那么修长，以至于掌跟触着我一边的胸腔，指尖还能着另一边。我的心跳得如此厉害，以至于胸口都有些疼了，我盯着他，眼睛睁得大大的。

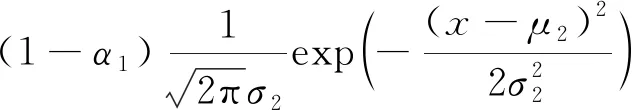
(1)

式中：为时刻；=0830 3，为出发前往工作地点时刻，属于第一个高斯模型概率；=7194 4 和=13147 7 分别为第一个和第二个高斯模型均值；=1508 0 和=8719 2分别为第一个和第二个高斯模型方差.

工作日电动汽车离开工作地点返回住宅区时刻符合高斯分布，概率密度表达式为

()=

(2)

式中：=17.197 2，为离开工作地点时刻均值；=2.619 7，为离开工作地点时刻方差.

每日出发前往工作地点与从工作地返回住宅耗时均符合对数正态分布，概率密度表达式为

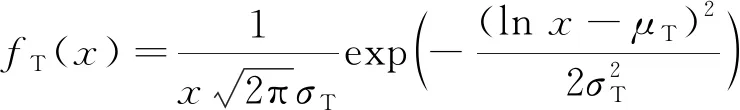
(3)

式中：=-1.052 6，为行程耗时期望均值；=0.749 1，为行程耗时方差.

每日行驶里程符合对数正态分布，概率密度表达式为

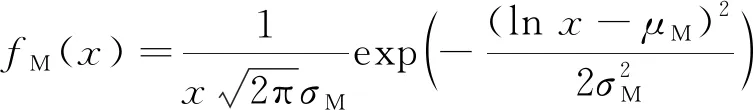
(4)

(3) 基于Gap statistic算法确定最佳聚类数.基于白天、夜间出力特征值矩阵，用Gap statistic 算法分别确定最佳聚类数.

1.2 假设条件

单台电动汽车充电需求主要受电动汽车种类、行驶规律和充电功率等3个方面影响.参考目前电动汽车发展情况，对家用电动汽车作出如下假设：

(1) 百千米耗电为16.7 kW·h.

(2) 电动汽车一天仅需充电一次，电池容量为70 kW·h.

(3) 在工作区，如果时间允许，电动汽车采用慢充方式充电，否则采用快充方式充电；在住宅区，电动汽车采用慢充方式充电；电动汽车充电过程为恒功率，快充、慢充充电功率分别为8 kW和60 kW.

山西体育中心体育馆工程是山西省重点工程，位于太原市晋源区，是一个能满足篮球、排球、乒乓球、羽毛球、体操、摔跤等国际单项比赛的大型场馆，建筑面积37 220 m2，总投资3.1亿元，可容纳观众8 102人。该工程是一项多功能、多设备、多专业、组织协调要求高、技术难度大的复杂工程，在两年多的施工中采用了许多新技术、新工艺和新材料，克服了施工过程中的许多难点，获得了市优良工程、省优良工程、太行杯和汾水杯奖等称号。

(4) 每次充电均充至满电量.

(5) 电动汽车每日出行时刻、出行耗时、日行驶里程均为独立分布.

1.3 基于蒙特卡罗方法的电动汽车无序充电模拟

假设待研究区域的电动汽车总数为40万辆，在无任何经济措施诱导和限制时，工作日有40%的电动汽车选择白天在办公区域进行充电，60%的车辆选择夜晚回家充电，用户均选择到达目的地后立刻充电，且每辆电动汽车在工作日的通勤规律一致.基于上述电动汽车行驶规律概率分布和假设条件，采用蒙特卡罗模拟法进行电动汽车无序充电模拟，单个用户具体模拟过程如下：① 抽取出发前往工作地点时刻1；② 抽取前往工作地点耗时，计算到达工作地点时刻2；③ 抽取从工作地点返家时刻3；④ 抽取从工作地点返家耗时，计算到家时刻4；⑤ 抽取总行驶里程，计算所需充电电量；⑥ 抽取电动汽车充电地点，判断电动汽车充电方式，生成充电功率曲线.

2 基于Gap statistic和K-means++算法的风光出力典型日划分模型

风电和光伏出力受风能、太阳辐射强度等多种因素影响，不同典型日出力场景下风光出力特性及其对电力系统的影响规律不尽相同；为分析不同典型日下，所提模型和优化调度方法的适用性和鲁棒性，基于风光出力预测数据，提出基于Gap statistic 和-means++算法的风光出力典型日划分方法，并用于不同典型出力场景下风光-电动汽车协同调度的差异化建模分析.

2.1 Gap statistic算法

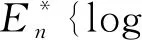
(1) 对已知观测数据集进行聚类，计算：

式中：()为常规机组在时刻出力.

(5)

式中：为第簇数据中组内点间的欧氏距离之和；为属于第簇的数据的个数；和为数据观测点；为第簇数据集合；=1, 2, …,

(6)

土壤侵蚀是在各种外营力的作用下，土壤物质被剥离、迁移、沉积的过程，是地球表面最普遍的自然地理过程，在一定程度上可以表征自然及人类活动综合作用的强度.侵蚀土壤不仅是河流及河口海岸输沙的主要来源，同时，被侵蚀土壤是各种养分及污染物质的载体，随雨水冲刷进入水中，对水环境的光学特性等物理性质及其化学与生物特性产生影响.入海河流及河口海岸带作为全球水环境的重要一环，其理化特性的改变，又对陆地气候等自然环境产生反馈反应.

(7)

式中：和为中间变量.

2.2 对风险的控制。对风险的控制是指风险管理人员在识别和衡量风险后，需要判别风险类型、风险值大小、风险潜在原因等，并以此制定合理的综合性防治措施，实现对风险的有效控制。风险控制中应用的主要手段包括指导书的编制、作业前的风险识别和落实重点措施等。

2.2 K-means++算法

-means++聚类算法是基于-means的改进算法，能够有效克服-means算法对孤立点较敏感，聚类结果易受初始聚类中心的影响等问题.-means++算法基本思想为假设已选取个初始聚类中心(1<<)，则在选取第+1个聚类中心时，距离当前个聚类中心越远的点会有更高的概率被选为第+1个聚类中心；随机选取第一个聚类中心(=1)-means++算法的具体步骤如下：

取清洁(CL)级ICR小鼠48只,随机分为6组,每组8只,试验前2 h禁止进食和饮水。分组包括4个精油组、空白对照组和地西泮组; 精油组用1%的吐温80溶液将苦水玫瑰精油或大马士革玫瑰精油分别稀释至0.01、0.1、1和10 mg/mL的浓度。

(1) 给定含有个样本的数据集=(,, …,)，从数据集中随机选取一个样本作为初始聚类中心.

新能源出力约束：

(8)

(3) 计算每个样本被选为下一个聚类中心的概率：

(9)

(8) 重复(6)～(7)直至聚类中心不再发生变化，从而得到最佳聚类结果.

(5) 重复(2)～(4)直至选取个聚类中心.

(6) 计算每个其他样本数据对象与各类聚类中心的距离，将其赋给最近的类.

(7) 计算每类数据对象的平均值，将其作为每一类新的聚类中心.

(4) 在[0, 1]区间生成一个随机数，用依次减去，，…，，取差值首次小于或等于0时对应的对象为下一个聚类中心.

2.3 风光出力典型日划分流程

基于Gap statistic和-means++算法的风光出力典型日划分的具体步骤如下：

(1) 数据采集及归一化处理.基于风电场和光伏电站预测出力数据获取新能源预测出力数据，采用最大最小归一化方法将其映射至[0, 1]区间，并将其处理为×96维新能源标准出力矩阵(为采样天数).

自1865年以来，ZENITH始终本着真实、勇敢和激情的宗旨，推动卓越、精准和创新。高瞻远瞩的制表师Georges Favre-Jacot在瑞士力洛克创立ZENITH之后不久，就获得了精密时计认证，并在短短一个半世纪的时间内荣获2333个精密时计奖项，创造了无与伦比的纪录。今天，ZENITH在测时方面又出新猷，其中包括测时精确到1/100秒Defy El Primero 21机心；并赋予世界上最精确的腕表21世纪的Defy Lab以全新机械精度。通过加强引以为豪的传统活力和前卫思想之间的纽带，ZENITH正在书写其未来……以及整个瑞士制表业的未来。

(2) 新能源出力特征值提取.考虑到光伏仅在白天存在出力，且新能源出力对夜间负荷影响较大，将每天6:00—18:00划分为白天，其余时间段划分为夜间，选取白天和夜间新能源出力均值和出力标准差作为特征值，得到两组×2维特征值矩阵.

式中：=2.831 4，为日行驶里程期望均值；=1.057 5，为日行驶里程方差.

(4) 基于-means++算法进行聚类分析.根据最佳聚类数，以白天、夜间出力特征值矩阵为输入，采用-means++聚类算法分别对白天、夜间新能源出力进行聚类分析.

(5) 白天和夜间聚类结果融合.采用时间对标法对白天和夜间聚类结果进行融合，获取不同出力场景下新能源出力.

(6) 不同出力场景典型日确定.由于融合后无法确定聚类中心位置，所以本文通过计算不同类别内各样本与其余样本的欧氏距离，以欧氏距离之和最小的样本序列为该类别的聚类中心，即该出力场景下的典型日.

3 风光-电动汽车协同调度模型

3.1 优化目标

等效负荷方差通过计算等效负荷在调度周期内的离散程度来衡量等效负荷整体波动性，负荷追踪系数通过比较新能源出力与负荷的时序波动特性来衡量新能源出力与负荷的匹配程度.考虑等效负荷整体波动和风光出力与负荷的匹配度，构建以等效负荷方差和负荷追踪系数最小为双优化目标的风光-电动汽车协同调度模型.

(1) 等效负荷方差().等效负荷方差主要衡量等效负荷整体波动性：

(10)

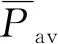
(2) 负荷追踪系数.等效负荷方差仅能衡量等效负荷整体波动性，无法衡量风光出力与负荷的匹配度.为了使风光互补发电系统能够更好地跟随负荷变化，保障系统安全稳定运行，从源荷匹配度角度出发，采用能够衡量风光出力与负荷匹配关系的负荷追踪系数()为优化目标：

周边居民没人明白何故又修这条路，阿东更是不介意。阿东每天骑车直接从东亭拐入东湖路。他不需要迎宾大道，修不修这条路跟他的生活毫无关系。阿东眼下的满门心思是要不要去追资料员小丁。他觉得自己是有点喜欢她的了。他甚至暗中了解到她是师专毕业。阿东想，自己怎么也是硕士，就算家里穷，配一个大专生也应该是有资格的。

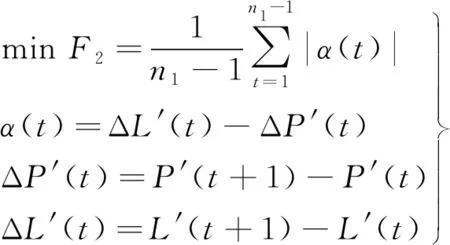
(11)

式中：′()和′()分别为最大最小归一化处理后时刻的新能源出力和负荷；Δ′()和Δ′()分别时刻为新能源出力和负荷的波动量标幺值；()为时刻新能源出力与负荷变化量变化的一致性.负荷追踪系数越接近于0，表明新能源出力与负荷在调度周期内的变化特性越一致，新能源联合出力与负荷匹配性越好.

（2）年际变化上，全疆、北疆、南疆线性倾向率均为正值，表明年降水量总体呈增加趋势；5a滑动平均过程线表示，年降水量总体呈显著增加趋势，局部（1970年代前后）呈不显著波动趋势。

3.2 约束条件

系统运行需满足如下约束.

系统功率平衡约束：

()+()=()

(12)

由图1可以看出，硫酸亚铁、硫酸铜和盐酸甜菜碱对金色链霉菌摇瓶发酵效价有促进作用，而氯化钴对其有抑制作用。硫酸亚铁在浓度0.002%时促进作用最明显，较对照提高15.9%；硫酸铜在浓度0.005%时促进作用最明显，较对照提高6.9%；盐酸甜菜碱在浓度0.03%时促进作用最明显，较对照提高9.6%；而氯化钴在浓度0.004%时抑制作用最为明显，较对照降低28.3%。因此可在基础发酵培养基中加入一定浓度梯度的硫酸亚铁、硫酸铜和盐酸甜菜碱以提高发酵效价。

(2) 计算每个样本与当前聚类中心之间的最短距离：

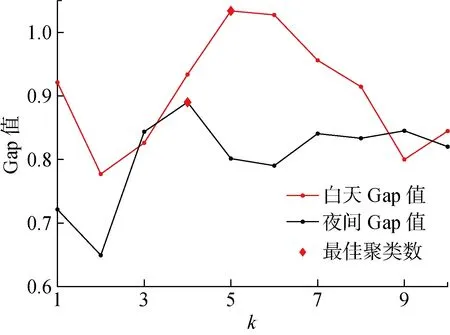
-means++算法需要事先确定聚类数目，对此采用Gap statistic算法分别确定白天、夜间新能源出力最佳聚类数，聚类范围选定为1～10类.白天、夜间不同聚类数下Gap值如图1所示.根据Gap statistic原理，当聚类数分别为5和4时，白天和夜间的Gap值第一次满足条件，因此确定白天和夜间最佳聚类数分别为5类和4类.

猛一下子由无所事事的公务员转变为忙忙碌碌的打工者，工作节奏的骤然加快，令高潮很长时间都难以适应。在经过几次老板炒他鱿鱼和他炒老板鱿鱼之后，高潮终于决定不打他娘的工了，自己做老板。对于创业的规划，高潮从打工那天开始，就一直在心里暗暗盘算。因为高潮发表过一些诗歌，认为自己是个不折不扣的文化人了，因此，他都是选择到一些杂志、网站做编辑，对这些身份不太明确的媒体的运作程序渐渐有所了解。甫一辞职，高潮就花了伍佰圆钱，请人做了一个名为“焦点调查”的网站，开始了他的创业之旅。

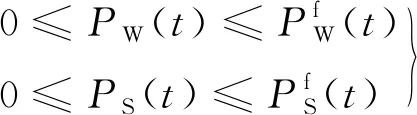
(13)

≥′

(14)

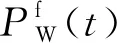
电动汽车电量约束：

≤()≤

(15)

(+1)=()+()Δ

(16)

式中：()为时刻电动汽车电量；和分别为电动汽车电池储存容量的上下限；()为时刻电动汽车充电功率；Δ为充电时长.

3.3 求解方法

所提风光-电动汽车协同调度模型为多目标优化问题，采用NSGA-II多目标优化算法进行模型求解.NSGA-II算法通过引入快速非支配排序技术，提高了算法的速度，具有结构简单、收敛速度快、鲁棒性能好的优点，算法具体实施步骤见文献[21].

在多目标优化问题中，一般不存在一组解使得所有目标函数值同时达到各自的最优值，只能求得非支配解集或 Pareto解集.因此，本文采用模糊隶属度函数分别表示每个Pareto解中各目标函数对应的满意度，通过满意度比较找出最优折衷解.

4 算例分析

基于中国西北某省2019年风光电站预测出力和电网预测负荷数据进行算例分析，数据时间长度为1年，时间分辨率为15 min.风电、光伏以及电网负荷比约为11∶9∶13，风电场并网装机容量为 11 160 MW，光伏电站并网装机容量为 9 180 MW，电网最大负荷为 12 900 MW，风光装机容量达全省总装机容量的40%，属于高比例新能源电网；假定该省共有40万辆电动汽车可供调度.

4.1 典型日划分

受后期构造影响，部分矿体形态会变得复杂，如出现分支复合和犬牙交错现象。褶皱过程中，岩层(或矿层)在翼部的物质向着核部塑性流动，尤其为紧密褶皱时，在向斜核部有矿层加厚现象。在后期的混合岩化作用下，磁铁石英岩中的部分磁铁矿颗粒变粗。

采用-means++算法对新能源出力特征值进行聚类分析，聚类结果如图2所示.新能源白天出力可划分为5类波动情况，夜间出力可划分为4类波动情况.从均值看，白天对应的低出力小波动、低出力波动、中出力波动、高出力波动、高出力大波动分别分布在(0.05，0.22)、(0.21，0.33)、(0.32，0.43)、(0.44，0.58)、(0.56，0.75)区间；夜间对应的低出力小波动、低出力波动、中出力波动、高出力波动分别分布在(0，0.13)、(0.11，0.24)、(0.19，0.32)、(0.30，0.48)区间.从方差看，白天对应的低出力小波动、低出力波动、中出力波动、高出力波动、高出力大波动的方差逐渐增大，表明新能源出力波动越大；夜间对应的低出力小波动、低出力波动、中出力波动方差逐渐增大，高出力波动时新能源出力波动性有所降低，表明夜间风电高出力时全省风电平滑效应较好.

采用时间对标法对白天和夜间聚类结果进行融合，获取不同典型日对应的新能源出力，如图3所示.图中，时间分辨率为15 min，全年共可划分为16类典型日，不同典型出力场景下新能源出力具有一定差异性，但同时具有一定相似性，且白天出力较大.将其按照出力大小进行划分，主要可划分为全天低出力波动(典型日1～4)，主要包括白天、夜间低出力场景，出现率为43.73%；白天低出力波动(典型日5和6)，主要包括白天低出力、夜间中出力场景，出现率为5.29%；夜间低出力波动(典型日7～10)，主要包括夜间低出力和白天中、高出力场景，出现率为27.30%；中出力波动(典型日11～14)，主要包括白天、夜间中出力场景，出现率为15.04%；全天高出力波动(典型日15和16)，主要包括白天、夜间高出力波动场景，出现率为8.64%；该地区新能源出力主要为全天低出力类型.

4.2 风光-电动汽车协同调度结果

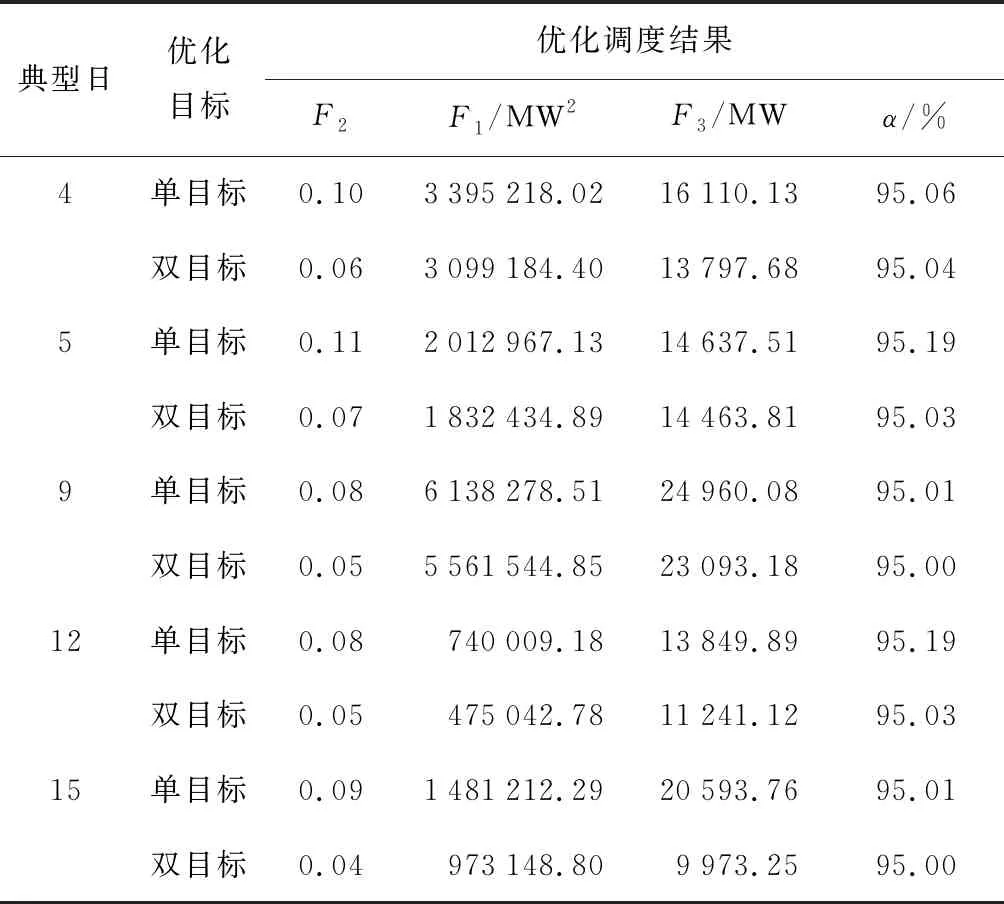
为验证所提模型的适用性和鲁棒性，根据图3典型日划分结果，随机选取5种典型日出力场景，分别构建以等效负荷方差最小为单优化目标、以等效负荷方差和负荷追踪系数最小为双优化目标的风光-电动汽车协同调度模型，以等效负荷峰谷差()为指标评价不同优化结果.单目标优化模型采用遗传算法进行求解，各项参数与NSGA-II 算法具有相同设置.5种典型日出力场景下优化调度结果如表1所示.不同典型日出力场景下，相比单目标优化调度模型，双目标优化调度模型的等效负荷峰谷差平均降低了19%.表明所提优化模型可以在降低等效负荷整体波动性的基础上，提升新能源出力与电网负荷匹配度，缓解风光出力和电动汽车无序充电等多重不确定性对电力系统的不利影响，且在不同典型出力场景下均具有良好的适用性和鲁棒性.

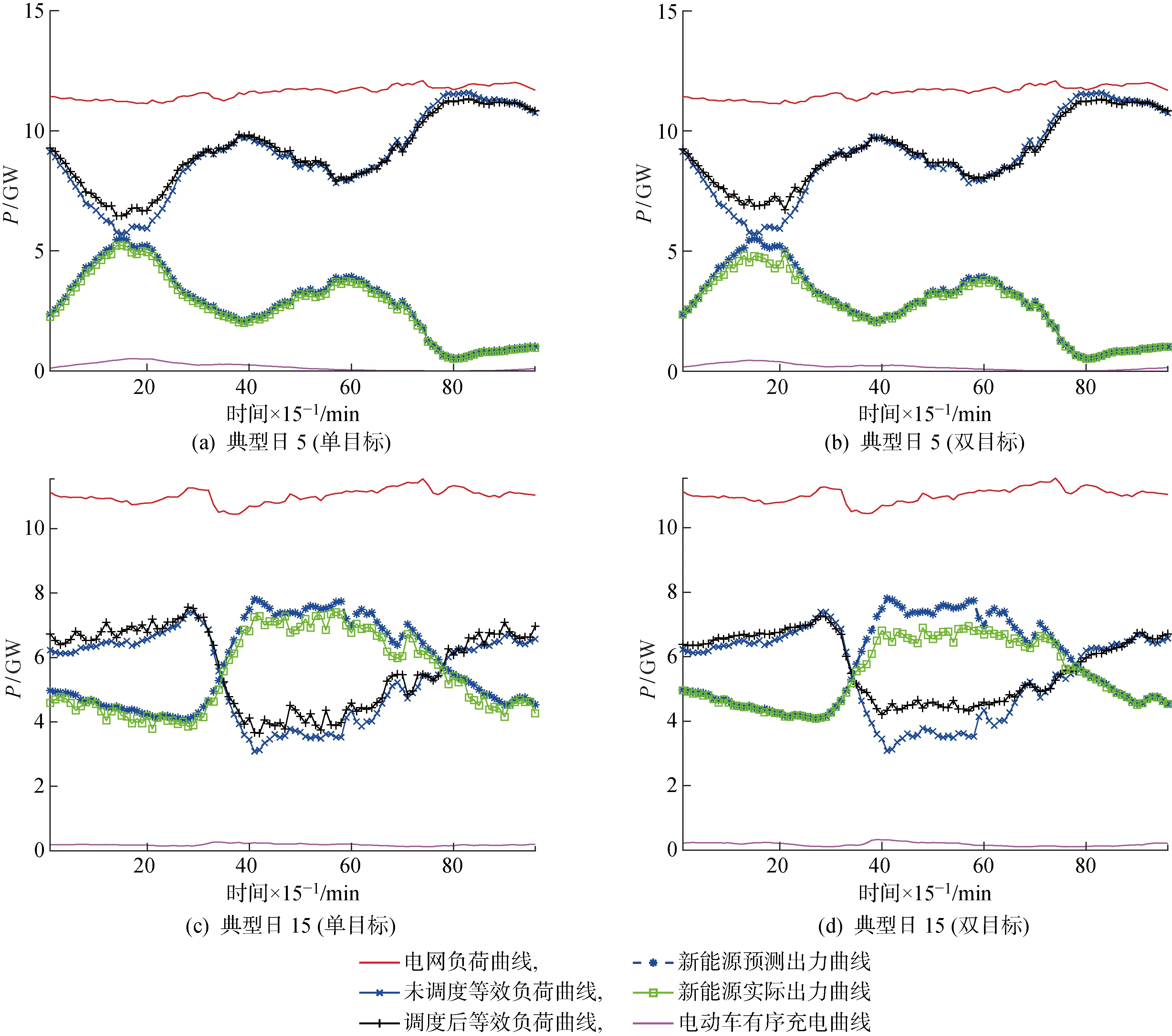
为分析不同典型日对优化调度结果的影响，选取出力情况差异较大的典型日5和15进行具体分析，如图4所示，其中为功率.在图4(a)和4(b)中，从新能源预测出力曲线可知，典型日5在凌晨 2:00—5:00 出力较大；未进行调度时在 5:00 左右等效负荷波动存在低谷期.对比图4(a)和4(b)新能源实际出力曲线可知，双目标优化时限电时刻更集中，主要发生于凌晨 3:00 左右；对比电动汽车有序充电曲线可知，二者整体趋势相似，均集中于凌晨进行充电.

图4(c)和4(d)中，从新能源预测出力曲线可知，典型日15新能源出力主要集中在白天10:00—14:00；未进行优化调度时，受新能源出力影响，等效负荷在午间存在低谷期且该时段内波动较大.对比图4(c)和4(d)可知，双目标优化限电主要集中于等效负荷低谷期；电动汽车充电时段尽可能集中于新能源出力最大时期，在全天其余时段，则尽可能平滑充电以降低对电网负荷的影响.

对比不同典型日双目标优化结果可知，新能源出力限电行为均主要发生在新能源出力较大和等效负荷波动较大的时刻；优化后电动汽车充电曲线根据典型日出力特性不同，随新能源出力变化而变化以降低新能源出力对电网负荷的影响.

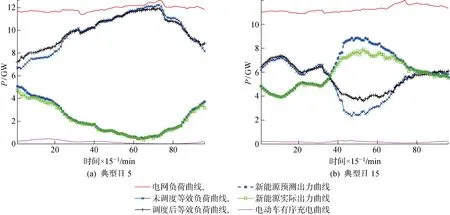
为进一步分析出力场景对优化调度结果的影响，分别从典型日5和15中任选一天进行风光-电动汽车协同调度，与典型日优化调度结果进行对比分析，优化结果如图5所示.

图5中，不同出力场景下，优化后新能源限电行为均集中于出力较大时刻.对比图4(b)与图5(a)可知，调度后电动汽车主要集中于夜间充电以降低新能源出力对电网负荷的不利影响；对比图4(d)与图5(b)可知，虽然新能源高出力时段存在差别，但电动汽车充电均集中于中午12: 00.受新能源出力特性影响，在同一出力场景下，电动汽车充电效果具有很强的相似性；在不同出力场景下电动汽车充电效果具有明显的差异性.

综上所述，在不同出力场景下，电动汽车充电效果主要与此类典型日固有特征相关；所提优化调度模型在不同典型出力场景下均具有良好的适用性与鲁棒性.

5 结论

提出一种面向高比例新能源并网场景的风光-电动车协同调度方法，所得结论如下：

(1) 基于Gap statistic和-means++算法的风光出力典型日划分模型能够实现白天和夜间新能源出力典型日的有效划分，新能源白天出力可划分为低出力小波动、低出力波动、中出力波动、高出力波动、高出力大波动共5类波动情况；夜间出力可划分为低出力小波动、低出力波动、中出力波动、高出力波动共4类波动情况，融合后共划分为16类典型出力场景.

通过农业推广渠道，建立“机构+企业+基地+农户”的联结机制，以科技创新消除产业融合的经济技术障碍。加大农村科研平台建设力度，全面完善科技创新体系，重点打造农村一、二、三产业可持续发展平台。鼓励企业加大研发力度，加快研发符合市场需求的养殖、种植新工艺、新品种、新技术。

(2) 以等效负荷方差和负荷追踪系数最小为双优化目标的源荷协同调度模型能够有效降低等效负荷波动性，提高新能源出力与电网负荷匹配度，从而减轻高比例可再生能源场景下风光出力和电动汽车无序充电不确定性对电力系统的不利影响.