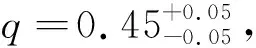ZTF J060524.16+244923.4的双星解轨和物理参数研究
代 敏,王 坤,曹星梅,陈 涛
(西华师范大学 物理与天文学院,四川 南充 637009)
质量、半径、光度等物理量是表征恒星物理性质最重要的几个参数,而测定这些物理参量仍然是现代天体物理研究中的一个基础性工作。食双星(Eclipsing Binary,简称EB)是指两个天体在引力的作用下围绕公共质心运动,相互绕转彼此遮掩而造成亮度、轨道视向速度发生规律性变化的双星系统。双星的动力学问题是一个二体问题,其对应的运动方程是可以严格解出的[1]。一方面,通过测光、光谱观测可获取反映子星亮度、运动状态等数据资料;另一方面,理论上可以给出子星的位置、速度以及辐射强度等参量。因此,可以构建食双星模型分析软件对观测资料进行拟合,从而给出描述两子星的物理参量。综合光变曲线和视向速度解轨分析结果,不依赖任何恒星结构模型,利用基本的物理定律可以计算出掩食双星系统子星的质量、半径、光度等物理参量。目前,通过此方法求得的恒星质量误差小于1%[2]。
随着现代天文学的快速发展,出现了许多测光和光谱巡天项目,如ZTF、LAMOST、SDSS[3]、TESS[4]、Kepler[5]、APOGEE[6]等。ZTF是一个拥有g波段和r波段的时域巡天项目,使用Palomar 48英寸施密特望远镜,拥有一个47平方度的视场和一个600万像素的照相机,以3760平方度每小时的速度对北天进行巡天拍摄,中值极限星等为20.8等(g波段)和20.6等(r波段)[7]。LAMOST又名郭守敬望远镜,它使用了一架反射式施密特望远镜,其焦面上安装了4000根光纤,可以同时观测20平方度视场内的4000个目标,其中低分辨率光谱覆盖了3690~9100 Å的波长,在5500 Å处的分辨率约为1800[8-9]。基于这些大规模巡天望远镜产生的观测数据,天文学家已经在食双星相关研究领域取得了丰硕的成果,例如Burdge等[10]基于ZTF测光数据发现了一个 8.8 min道周期的分离双白矮星食双星系统,确定了其物理参数并研究了其演化过程;基于TESS测光数据和APOGEE光谱数据,Miller等[11]研究了一个子星带有黑子的亚太阳食双星系统;基于Kepler测光数据,Miszuda等[12]深入研究了一个子星为δ Scuti星的食双星系统;基于LAMOST光谱数据,Qian等[13]研究了处于不同演化阶段的相接双星系统;基于SDSS测光数据,Kosakowski等[14]对短周期双简并食双星系统进行了研究;基于APOGEE光谱数据,Kounkel等[15]对双线光谱双星系统进行了研究。
Henize等[16]在2018年把ZTF J060524.16+244923.4(又名ATO J091.3506+24.8231)作为食双星候选体。Chen 等[17]给出了ZTF J060524.16+244923.4的周期、光变曲线特征等信息,并把光变曲线归类为EA型。本文使用ZTF测光数据星表[18]与LAMOST DR8低分辨率光谱星表进行交叉匹配,得到食双星系统ZTF J060524.16+244923.4的时序光变曲线和视向速度曲线。第一节介绍了ZTF J060524.16+244923.4的测光数据和光谱数据,第二节使用PHOEBE[19]程序对ZTF J060524.16+244923.4的光变曲线和视向速度曲线进行分析,在最后一节对本文进行和总结和讨论。

表1 ZTF J060524.16+244923.4食双星系统基本参数
1 观测数据
食双星系统ZTF J060524.16+244923.4的基本参数见表1。
1.1 光变曲线
从ZTF DR5官网(https://irsa.ipac.caltech.edu/cgi-bin/Gator/nph-dd)下载ZTF J060524.16+244923.4的光变曲线数据,为了保证光变曲线质量,只选择了“catflag”小于 10的高质量测光数据。图1与图2分别展示了ZTF J060524.16+244923.4的r波段和g波段的相位化和流量归一化之后的光变曲线。其中极小时刻t0的HJD时间为2 458 206.086 5,来源于PHOEBE程序的“lc估算器”。

1.2 光 谱
ZTF J060524.16+244923.4的光谱数据来源于LAMOST DR8官网,其中g波段和r波段的信噪比均大于10,共获得25个光谱。有效温度(Teff)、表面重力(log g)、金属丰度(Fe/H)、视向速度(RV)来源于LAMOST恒星参数计算软件(LASP)计算的结果。图3展示了ZTF J060524.16+244923.4的一条低分辨率光谱,该光谱的拍摄时间为2016年11月23日,r波段和g波段的信噪比分别为153.7和110.77 。图4展示了相位化之后的视向速度曲线。
2 解轨分析
利用ZTF的测光数据和LAMOST的光谱数据,用PHOEBE程序对ZTF J060524.16+244923.4的光变曲线(LC)和视向速度曲线(RV)进行分析。根据光变曲线的形状,尝试了分离模型和半相接模型,最终选择使


表2 固定的参数

表3 拟合的参数
用半相接模型进行建模分析。表2、表3呈现了固定的参数和进行拟合的参数情况。固定该双星系统的轨道周期为1.280 922 6 d,主星的有效温度为6679.5 K,由于主星大气参数在ck2004大气模型范围内,设置大气模型为“ck2004”模型[20]。双星系统的极小时刻(t0)的初始值由PHOEBE的“LC估算器”得到;通过“RV估算器”模块,得到了主星半长轴与双星系统倾角的正弦值的乘积(asini)、轨道偏心率(ecc)、轨道近星点角距(per0)和双星系统速度(Vgamma)的初始值。通过“EBAI”神经网络得到了双星系统的轨道倾角(i)、次星与主星的温度比(T2/T1)、半径和与半长轴之比[(R1+R2)/sma]等参数的初始值。接下来,使用基于EMCEE[21]的Markov chain Monte Carlo (MCMC)确定此双星系统的物理参数值和误差,见图5。在进行的第一次MCMC采样中,选择固定轨道相关的参数,只计算了光变曲线相关的参数,得到了t0、q、R1、T2/T1。最后,根据第一次MCMC采样的结果,重新计算t0、i、sma、q、R1、T2、esinw、ecosw、Vgamma以及r波段光度和g波段光度等物理参数,运行了500次程序迭代,每次迭代使用了30个步长,最终得到ZTF J060524.16+244923.4双星系统的物理参数和误差。
表4是最终得到的ZTF J060524.16+244923.4双星系统的物理参数和误差。图6、图7分别是光变曲线和视向速度曲线的最佳拟合图与残差图,其中,光变曲线的r波段和g波段的残差的标准差分别为0.018 W·m-2和0.015 W·m-2;视向速度残差的标准差为10.00 km·s-1。虽然低分辨率光谱只能得到单线视向速度,不能直接得到质量比,但通过图5可以看到所有的参数都呈现出近高斯分布,这说明得到的物理参数是比较可靠的。


表4 ZTF J060524.16+244923.4双星系统物理参数

3 结果与讨论