求解拟变分不等式的次梯度外梯度算法

田倍昕，赵 丹，叶明露

(西华师范大学 数学与信息学院，四川 南充 637009)

20世纪以来，纳什均衡问题广泛应用在经济、政治等领域。该理论假设了每个竞争者的策略集是一个与其他竞争者无关的常值集合，广义纳什均衡问题则假设每个竞争者的策略集都取决于其他人的决策。因此，广义纳什均衡问题的这种结构更接近于竞争市场的真实情况，引起了广大学者的关注，参见文献[1-3]。在一定条件下，纳什均衡问题等价于一个变分不等式问题，而广义纳什均衡问题则等价于一个拟变分不等式(简称QVI)问题。

uk=(1-bk)xk+bkPC(xk)[xk-αF(xk)],xk+1=(1-ak)xk+akPC(uk)[uk-αF(uk)],k=0,1,2,…

该算法在映射F强单调且Lipschitz连续(需要知道Lipschitz系数或者上界)，c(x)Lipschitz连续且C0是一个闭凸集时得到了全局收敛性。受文献[6]与文献[13]的启发，本文在文献[7]的基础上提出一种新的步长，使得新算法适用于映射单调且Lipschitz系数值未知的情况，并且该算法的每次迭代只需计算一次向可行集的投影。同时在适当的假设下，得到了算法的收敛性结果。

1 基本概念

本节给出文章需要用到的基本概念以及基础知识。设Rn为n维欧氏空间，X为Rn的非空子集。用〈·,·〉和‖·‖分别表示Rn中的内积和范数。

设F：Rn→Rn是一个单值映射，K∶Rn⟹Rn是一个集值映射，并且其值为一个非空闭凸集。在上述条件下，本文考虑的拟变分不等式问题如下：寻找向量u*∈X，使得u*∈K(u*)且满足下述不等式

〈F(u*),v-u*〉≥0，∀v∈K(u*)。

(1)

对上述问题而言，如果对于任意的u∈Rn都有K(u)≡K成立，问题(1)退化成经典的变分不等式问题。即找到一个向量u*∈K使得

〈F(u*),v-u*〉≥0， ∀v∈K。

(2)

接下来将回顾一些定义、性质、引理及一些与其相关的结论。

定义1[13]X为Rn的非空闭凸子集，给定映射T∶Rn→Rn，称

(1)映射T在X上是L-Lipschitz连续的，且Lipschitz系数L>0，如果

‖T(x)-T(y)‖≤L‖x-y‖, ∀x,y∈X；

(3)

(2)映射T在X上是单调的，如果

〈T(x)-T(y),x-y〉≥0, ∀x,y∈X。

(4)

引理1[13]设C是Rn上的非空闭凸集，对于任意的x∈Rn，都在C中存在唯一的一点，使得该点与x的距离最近，称这个点为x在C上的投影，记作PC(x)，即

‖x-PC(x)‖≤‖x-y‖, ∀y∈C。

(5)

投影映射PC∶Rn→C还满足下式性质

〈x-PC(x),PC(x)-y〉≥0, ∀x∈Rn,∀y∈C。

(6)

同时，该映射PC∶Rn→C也是非扩张的，即

‖PC(x)-PC(y)‖≤‖x-y‖， ∀x,y∈Rn。

(7)

通过引理1，可以得到下面的引理。

引理2 设C是Rn上的非空闭凸集，xk+1=PC(xk)，z∈C，则有下式成立

‖xk+1-z‖2≤‖xk-z‖2-‖xk+1-xk‖2。

(8)

引理3[14]设K(·)是Rn中具有非空闭凸值的集值映射，则x*∈K(x*)是拟变分不等式的一个解，当且仅当对于任何τ>0，都有x*=PK(x*)(x*-τF(x*))成立。

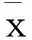
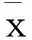
vk→z(k→∞)；

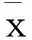
(d)在X上连续当且仅当它在X上的每个点都是连续的。

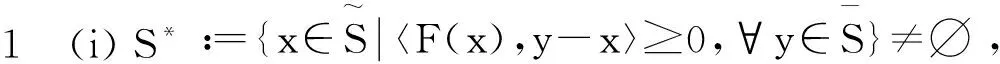
注1 记拟变分不等式的解集S∶={x∈X|〈F(x),y-x〉≥0,∀y∈K(x)}。则由S*与S的定义可知S*⊂S。因此，S*≠∅的假设比S≠∅的假设更强。但若对于所有x∈X，都有K(x)≡K成立，即拟变分不等式问题退化为变分不等式问题，则有S*=S。此时该假设退化为S≠∅。因此，假设(i)也被文献[13-15]作为求解QVI的一个基本假设。注意到文献[7]中假设的集值映射C必然是连续的，且其值是一个非空的闭凸集。因此，(ii)的假设条件更弱，并且该假设也被文献[13-15]作为求解QVI的一个基本假设。

2 算 法

在这一部分，将介绍一种新的步长去求解拟变分不等式问题。

算法1

步骤1 选取两个参数λ1>0,μ∈(0,1)，初始点x1∈X，令k=1。计算yk=PK(xk)(xk-λkF(xk))，如果yk=xk，则算法停止，否则执行步骤2。

步骤2 计算xk+1=PTk(xk-λkF(yk))，其中Tk={ω∈X∶〈xk-λkF(xk)-yk,ω-yk〉≤0}。更新

(9)

注2 如果yk=xk，根据算法1可以得到yk=PK(yk)(yk-λF(yk))，由引理3知yk为拟变分不等式的一个解。

3 收敛性分析

证明由λk+1的定义可知{λk}为一非负单调递减数列，从而其极限存在。下面用数学归纳法来证明

(10)

若F(yk)≠F(xk)，那么由映射F的Lipschitz连续性可以得到

定理2 考虑映射F具有单调性和L-Lipschitz连续性的QVI问题。设{xk}，{yk}是由算法1生成的任意序列，x*为解集S*中的任意一点，则有下面的不等式成立：

(11)

证明由于x*为解集S*中的一点可知x*∈K(xk)，再结合引理1中(6)式可得

〈xk-λkF(xk)-yk,x*-yk〉≤0。

由半空间Tk的定义可知x*∈Tk。再结合引理2则有下式成立

‖xk+1-x*‖2≤‖xk-λkF(yk)-x*‖2-‖xk-λkF(yk)-xk+1‖2

=‖xk-x*‖2-2〈xk-x*,λkF(yk)〉-‖xk-xk+1‖2+2〈xk-xk+1,λkF(yk)〉

=‖xk-x*‖2-‖xk-xk+1‖2-2〈xk+1-x*,λkF(yk)〉

=‖xk-x*‖2-‖xk-xk+1‖2-2〈yk-x*,λkF(yk)〉-2〈xk+1-yk,λkF(yk)〉。

(12)

利用映射F单调性、x*∈S*以及λk>0的这个事实，可以得到

〈yk-x*,λkF(yk)〉=〈yk-x*,λkF(x*)〉+〈yk-x*,λk(F(yk)-F(x*))〉≥0 。

(13)

结合(12)式与(13)式可得

‖xk+1-x*‖2≤‖xk-x*‖2-‖xk-xk+1‖2-2〈xk+1-yk,λkF(yk)〉

=‖xk-x*‖2-‖xk-yk‖2-‖yk-xk+1‖2-2〈xk-yk,yk-xk+1〉-2〈xk+1-yk,λkF(yk)〉

=‖xk-x*‖2-‖xk-yk‖2-‖yk-xk+1‖2-2〈xk-λkF(xk)-yk,yk-xk+1〉-

2〈yk-xk+1,λkF(xk)〉-2〈xk+1-yk,λkF(yk)〉。

因为xk+1∈Tk，由半空间的定义可得〈xk-λkF(xk)-yk,yk-xk+1〉≥0。因此，

‖xk+1-x*‖2≤‖xk-x*‖2-‖xk-yk‖2-‖yk-xk+1‖2-2〈yk-xk+1,λkF(xk)〉-2〈xk+1-yk,λkF(yk)〉

=‖xk-x*‖2-‖xk-yk‖2-‖yk-xk+1‖2+2λk〈F(xk)-F(yk),xk+1-yk〉

≤‖xk-x*‖2-‖xk-yk‖2-‖yk-xk+1‖2+2λk‖F(xk)-F(yk)‖‖xk+1-yk‖。

(14)

下面对2λk‖F(xk)-F(yk)‖‖xk+1-yk‖的值进行分类讨论：

(i)如果‖F(xk)-F(yk)‖≠0，根据λk+1的定义可得

(15)

其中第二个不等式是由a2+b2≥2ab得到的。

(ii)如果‖F(xk)-F(yk)‖=0,则(15)式也成立。

综上所述，(15)式成立。结合(14)式与(15)式可得(11)。

定理3 如果假设1成立且{xk}为由算法1生成的无穷序列，则下述结论成立

2)序列{xk}有界，且其任一聚点都是拟变分不等式的一个解。

(16)

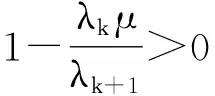
‖xk+1-x*‖2≤‖xk-x*‖2，k>N。

2)由1)知数列{xk}有界。设u为其任一聚点，则存在指标集I⊂N使得xk→u(k∈I,k→∞)。下证聚点是拟变分不等式问题(1)的解。为此，先证明u∈K(u)。由(11)式可得

(17)

(18)

进而由迫敛性可得

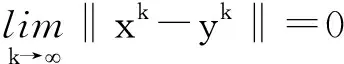
(19)

由此，结合不等式‖yk-yk-1‖≤‖yk-xk‖+‖xk-yk-1‖可知

(20)

由(19)式结合所设xk→u(k∈I,k→∞)可得yk→u(k∈I,k→∞)。进而结合K的上半连续性以及yk∈K(xk)的这个事实可以推出u∈K(u)。

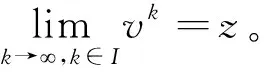
〈yk-xk+λkF(xk),v-yk〉≥0, ∀v∈K(xk),∀k∈I。

(21)

特别地，对任意的k∈I有

0≤〈yk-xk+λkF(xk),vk-yk〉

=〈yk-xk,vk-yk〉+〈λkF(xk),vk-yk〉

=〈yk-xk,vk-yk〉+〈λkF(xk),vk-xk〉+〈λkF(xk),xk-yk〉。

(22)

0≤〈F(u),z-u〉, ∀z∈K(u)。

上式结合u∈K(u)可知u为拟变分不等式问题(1)的解。

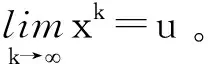
证明因为u是序列{xk}的聚点，故根据定理3可知

〈F(u),z-u〉≥0,∀z∈K(u)。

(23)

设x*为解集S*中的一点，再结合yk∈K(xk)及S*的定义可得

〈F(x*),yk-x*〉≥0。

(24)

在(24)式中令k→∞，k∈I，再结合(19)式与u是序列{xk}的聚点的这个事实可得

〈F(x*),u-x*〉≥0。

(25)

进而，结合F的单调性可得

〈F(u),u-x*〉≥0。

(26)

由S*的定义知x*∈K(u)，从而由(23)可得

〈F(u),x*-u〉≥0 。

(27)

同理结合(27)式与F的单调性可得

〈F(x*),x*-u〉≥0 。

(28)

结合(26)式与(27)式可得〈F(u),x*-u〉=0，结合(25)式与(28)式可得〈F(x*),x*-u〉=0。

由此可得〈F(x*)-F(u),x*-u〉=0，再结合F在u点的严格单调性可得u=x*∈S*。

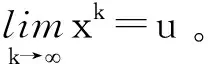
4 结 语

本文提出了一种新的步长规则来求解QVI问题，在映射单调且Lipschitz系数难以估计的情况下证明了算法的强收敛性。本文的算法相较于文献[7]拥有更加广泛的适用范围。