关于抛物-抛物热传导Keller-Segel类模型的全局解
林清芸,吴 杰
(1.电子科技大学 数学科学学院,成都 611731;2.成都大学 计算机学院,成都 610106)
近年来,趋化-流体模型[1-2]已成为生物数学领域中的一个前沿课题,许多数学家基于最经典的Keller-Segel模型[3-5]已经作出了许多贡献,特别是研究它定性的性质[6-11]。Duan等[12]研究了如下系统
这里,Ω为全空间R2或有界域。n、c、u、P和φ(x)分别表示细胞密度、氧气浓度、流体速度、相应的压强和势函数。正常数Dn、Dc、Du分别表示细胞扩散系数、氧气扩散系数和流体扩散系数。在一定初边值的假设条件下,他们证明了该系统的解是全局存在的。当系统中的Δn被Δnm,m>1取代时,文献[13-16]也给出了相应解的定性问题研究。
本文基于如下二维Keller-Segel型系统,即是上述模型系统第三个方程弱化的情形
(1)

n(x,0)=n0(x),c(x,0)=c0(x),
(2)
n和c满足无通量Neumann边界条件
(3)
这里ν为单位外法向量,u满足无滑边界条件
u=0,x∈∂Ω。
(4)
除此之外,假设
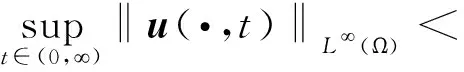
(5)
当化学物质的扩散很小,以至于可以忽略不计时,可在系统(1)中取ε=0,从而得到以下极限系统
(6)
并考虑它相应的初边值问题(2)—(4)。
本文的主要目的是证明抛物-抛物Keller-Segel型系统(1)和(2)—(4)的解收敛到相应抛物-热传导Keller-Segel系统(6)和(2)—(4)的解。为此,首先需要得到两系统的解的全局存在性。
为了考虑系统(1)和(2)—(4)解的全局存在性,先考虑如下更为一般的系统
(7)
这里,k(·)表示耗氧量。同时假设
(A)
(B)
1 准备工作
1.1 抛物-抛物型
首先给出系统(7)和(2)—(4)经典解的局部存在性和延拓定理。
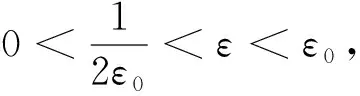

证明局部时间存在性利用Banach不动点定理证明,这里省略,具体细节参考文献[17-18]。同样唯一性的证明是标准的,这里省略不写。
以下引理给出系统(7)和(2)—(4)解的一般估计。
引理2 令(nε,cε)为系统(7)和(2)—(4)在Ω×(0,Tmax)上的经典解,如果Tmax<∞,则有
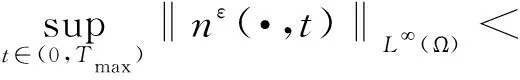
(8)
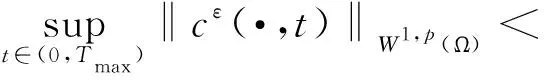
(9)
证明该引理的证明可以参考文献[12]直接可得。
由于系统(1)是系统(7)的特殊情况,故利用延拓定理和引理2,即可得到系统(1)和(2)—(4)解的全局存在性。
1.2 抛物-热传导型
首先,给出系统(6)和(2)—(4)经典解的局部存在性和延拓定理。

(10)
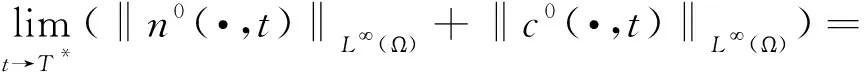
证明局部时间存在性利用Banach不动点定理证明,这里省略。同样唯一性的证明是标准的,省略不写。
以下两个引理给出了系统(6)和(2)—(4)解的基本估计。
引理4 令(n0,c0)为系统(6)和(2)—(4)在Ω×[0,T*)上的经典解,对任意的T∈(0,T*),则有
‖n0(·,t)‖L∞(Ω)≤‖n0‖L∞(Ω),t∈(0,T)。
(11)
证明对方程(6)1的两边同乘以p·(n0)p-1,分部积分则有
于是对所有的t∈(0,T*),‖n0(·,t)‖Lp(Ω)≤‖n0‖Lp(Ω),令p→∞可得(11)。
引理5 令(n0,c0)为系统(6)和(2)—(4)在Ω×[0,T*)上的经典解,对任意的T∈(0,T*),则存在一个仅依赖于Ω和初始值的正常数C使得
‖c0(·,t)‖L∞(Ω)≤C,t∈(0,T)。
(12)
证明假设z(s)=c0(x+tu,t+s),左右两边同时对s求导,则有

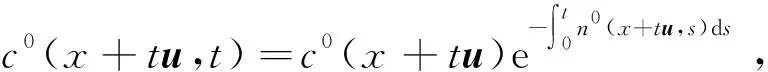
接下来,利用延拓定理即可得到系统(6)和(2)—(4)解的全局存在性。

证明根据引理3—引理5,应用延拓定理可证得定理1。
2 粘性消失极限
在这一节中,要证明本文最主要的结论,即当化学扩散系数ε→0时系统(1)和(2)—(4)的解收敛到系统(6)和(2)—(4)的解。首先提高两系统解的正则性估计。
引理6 对任意的T∈(0,T*),令(nε,cε)为系统(6)和(2)—(4)在Ω×[0,T*)上的经典解,假设(n0,c0)∈W2,p(Ω)×W2,p(Ω),这里p>2,那么存在一个依赖于Ω,T,p,ε0和初始值的常数C使得
(13)
证明根据抛物方程的Lp理论、Minkowski不等式、Gagliardo-Nireberg不等式、Young不等式、Sobolev嵌入定理、(5)式和引理2可知
‖cε‖Lp((0,T);W2,p(Ω))≤C1(‖u·∇cε+nεcε‖Lp((0,T);Lp(Ω))+‖c0‖W2,p(Ω))
≤C1‖u‖L∞((0,T);L∞(Ω))‖∇cε‖Lp((0,T);Lp(Ω))+‖cε‖L∞((0,T);L∞(Ω))‖nε‖L∞((0,T);L∞(Ω))+C1
≤C2‖∇cε‖Lp((0,T);Lp(Ω))+C3≤C4‖cε‖Lp((0,T);W1,p(Ω))+C3
故引理6成立。
类似于引理6的证明,可得如下引理7—9。
引理7 在引理6的假设条件下,存在一个依赖于Ω、T、p、ε0和初始值的常数C使得
(14)
引理8 对任意的T∈(0,T*),令(n0,c0)为系统(6)和(2)—(4)在Ω×[0,T*)上的经典解,假设(n0,c0)∈W2,p(Ω)×W2,p(Ω),这里p>2,那么存在一个依赖于Ω、T、p、ε0和初始值的常数C使得
(15)
引理9 在引理8的假设条件下,存在一个依赖于Ω、T、p、ε0和初始值的常数C使得

(16)
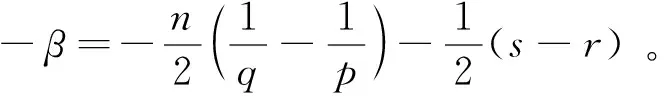
下面给出本文最主要的结果。
定理2 若初始值
(n0,c0)∈W2,p(Ω)×W2,p(Ω),p>2,
(17)
那么存在一个不依赖于ε的常数C使得
(18)
证明由Neumann热半群理论,有


=∶I1+I2+I3。
(19)
为了估计I1,利用Minkovski不等式和引理10可得
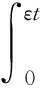
(20)


=∶I21+I22。
(21)
对于I21的估计,由Minkovski不等式、(5)式、引理6和引理9—10,存在正常数C1、C2使得

(22)
类似地,存在正常数C3、C4,可得I22的估计如下

(23)
同样地,为估计I3,可将I3改写成


=∶I31+I32。
(24)
由Minkovski不等式、Hölder不等式、引理6—10和嵌入定理,存在正常数C5、C6使得
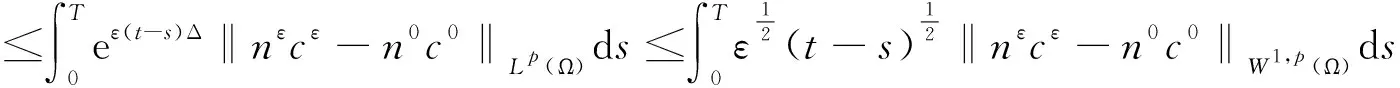
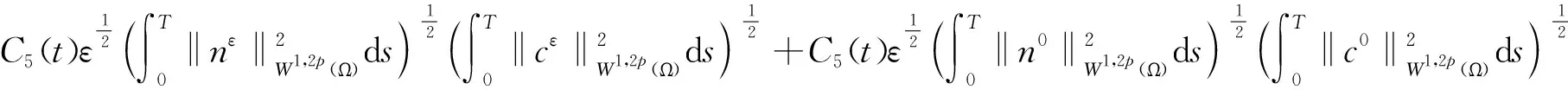
(25)
对于I32,同估计I22的方法一样,存在正常数C7,有
(26)
结合(20)—(26)式,存在正常数C(T)使得
(27)
下面讨论关于nε-n0的方程如下
(28)
对方程(28)1的两边同时乘以p(nε-n0)p-1并分部积分可得
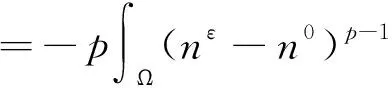
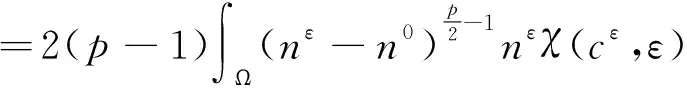
(29)
下面估计上式最后一项。由Hölder不等式和Young不等式,有


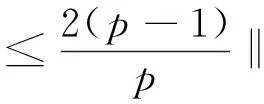
(30)
将(30)代入(29)可得
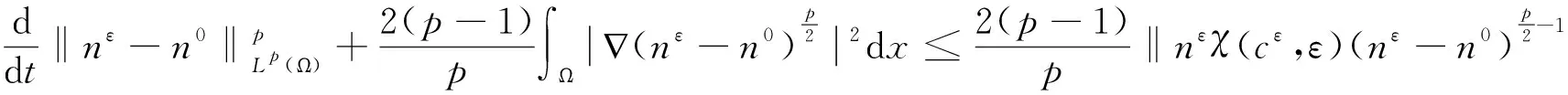
根据引理2和引理4,存在正常数C8,进而有
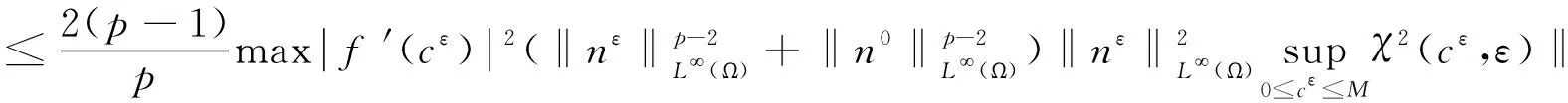
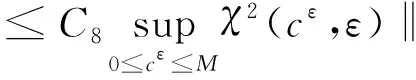
(31)
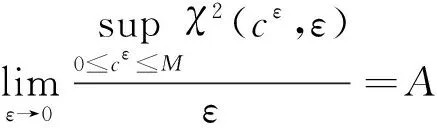

≤C11(t)εα
(32)
这里,α>1。因此由(27)和(32)式可证得本文的主要结果。

