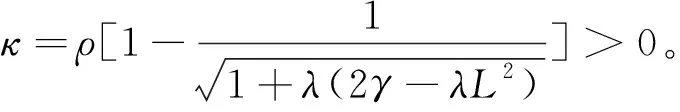求解强伪单调拟均衡问题的动力系统方法
常 浩,冯世强,李 军
(西华师范大学 数学与信息学院,四川 南充 637009)
均衡问题是一个非常普遍的数学模型,包括最优化问题、变分不等式问题、鞍点问题、非合作博弈Nash均衡问题、不动点问题等[1-4],它以一种简便的方式将所有这些特殊的问题统一起来。现有研究有很多关于均衡点的存在性和寻找均衡点的求解方法。由于均衡问题是一个通用模型,解决特定问题的方法通常可以扩展到均衡问题。这些方法的思想来源于求解变分不等式的邻近点方法和投影类方法。其中,不动点方法由于其形式简单、实用性强等优点,发挥着重要的作用。不动点方法能有效地求解一类强单调均衡问题,并且收敛速度是线性的。近年来,动力系统在求解不动点问题、变分不等式和单调性等方面得到了广泛的研究。为了研究脉冲控制问题,Bensoussan和Lions[5]引入了拟变分不等式。如今,拟变分不等式已经成为一种强有力的数学工具,用于解决在不同领域出现的各种复杂均衡问题,如广义纳什对策、经济和金融、力学、交通、统计学和生物学等。
2006年,Hu和Wang[6-7]研究了求解伪单调变分不等式的投影动力系统的收敛性,他们将凸优化问题的结果推广到伪凸优化问题,然而,为了得到全局指数稳定性,他们必须在强伪单调系数和相应算子的Lipschitz系数之间施加一些限制条件,但是强单调和Lipschitz连续变分不等式永远不满足这些条件。2018年,Ha等[8]研究了没有在强伪单调系数和相应算子的Lipschitz连续系数之间施加任何条件的基础上动力系统的全局指数稳定性。2020年,Nguyen和Qin[9]研究了强伪单调拟变分不等式投影动力系统的全局指数稳定性。Vuong和Strodiot[10]研究了强伪单调均衡问题动力系统的全局指数稳定性。结合以上研究,作为一种自然的延伸,对拟均衡问题的研究更具普遍意义。
由于求解拟均衡问题需要同时求解一个均衡问题和一个不动点问题,因此均衡问题解的存在性理论不能适用于拟均衡问题。本文研究了在强伪单调性和Lipschitz型连续性假设下,具有一般可变集A(·)且满足某种压缩性质的强伪单调拟均衡问题解存在唯一的充分条件。本文考虑了一个动力系统来求解拟均衡问题,并研究了动力系统均衡解的全局指数稳定性。
1 预备知识
令F:Rn×Rn→R是一个二元函数,A:Rn→2Rn是具有非空闭凸值的集值映射(对于每个x∈Rn,A(x)是Rn的非空闭凸子集),F(x,x)=0,且函数F(x,·)在Rn上是凸下半连续的。与F相关的拟均衡问题由QEP(F,A)表示:找到一点x*∈A(x*),使得
F(x*,y)≥0,
(1)
对所有的y∈A(x*)都成立,QEP(F,A)的解集表示为Sol(F,A)。
当F(x*,y)=〈f(x*),y-x*〉时,拟均衡问题QEP(F,A)退化为拟变分不等式问题QVI(f,A),找到一个点x*∈A(x*)使得〈f(x*),y-x*〉≥0对任意的y∈A(x*)都成立,其中,f:Rn→Rn是一个连续映射。
当A(x*)≡A是一个非空闭凸集时,拟均衡问题QEP(F,A)退化为经典的均衡问题EP(F,A),找到一个点x*∈A,使得F(x*,y)≥0对所有的y∈A都成立。
回顾一些在结果中有用的定义。
定义1 令X为Rn的一个非空闭凸子集,称映射F:X×X→R
(a)在X上关于系数γ>0强单调,如果F(x,y)+F(y,x)≤-γ‖x-y‖2对任意的x,y∈X都成立;
(b)在X上单调,如果F(x,y)+F(y,x)≤0对任意的x,y∈X都成立;
(c)在X上关于系数γ>0强伪单调,如果F(x,y)≥0⟹F(y,x)≤-γ‖x-y‖2对所有的x,y∈X都成立;
(d)在X上伪单调,如果F(x,y)≥0⟹F(y,x)≤0对所有的x,y∈X都成立。
备注1 (a)⟹(b),(a)⟹(c),(c)⟹(d)和(b)⟹(d)是显然的。还要注意的是,由文献[10]知,定义(c)保证EP(F,A)不可能有多解。
定义2[10]令X为Rn的一个非空子集,称映射F:X×X→R为X上关于系数L的Lipschitz型连续,如果存在L>0,使得
F(x,y)+F(y,z)≥F(x,z)-L‖x-y‖‖y-z‖,∀x,y,z∈X。
(2)

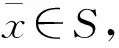
引理1[11]对于正常凸函数f∶Rn→(-∞,+∞]与任意实数λ>0必有
∂(λf)(x)=λ∂f(x),x∈Rn。
(3)
此外,给定正常凸函数fi∶Rn→(-∞,+∞](i=1,…,m),则有
∂(f1+…+fm)(x)⊇∂f1(x)+…+∂fm(x),x∈Rn。
(4)
若进一步还有ri domf1∩…∩ri domfm(x)≠∅,则(4)式中的反包含关系成立。
容易证明如下结论成立:
引理2 若ø≠S⊆Rn为凸集,x0∈S,则必有∂δS(x0)=NS(x0)。
2 解的存在性和唯一性
令x*∈Rn,对于每个λ>0,x∈A(x),考虑下面这个问题
(5)
由于F(x,·)是凸的,问题(5)是一个强凸问题,因此它有唯一的解。

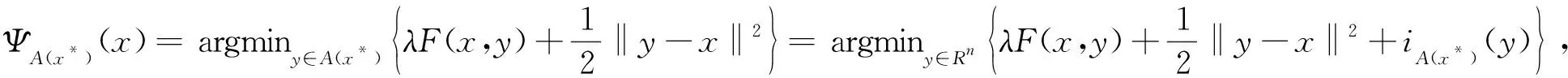
(6)
其中iA(x*)(y)是A(x*)上的示性函数。由问题(5)的性质可知,函数ΨA(x*)(x)良定的,且在A(x*)上只有一个值。
命题1 令x*∈Rn,对于任意的λ>0,x*∈Sol(F,A)当且仅当x*=ΨA(x*)(x*)。
证明充分性:令x*=ΨA(x*)(x*),则x*是问题(6)的一个解,则x*∈A(x*)且由引理1和引理2可得0∈λ∂F(x*,x*)+x*-x*+NA(x*)(x*),即0∈λ∂F(x*,x*)+NA(x*)(x*)。所以,存在z*∈∂F(x*,x*),使得0∈λz*+NA(x*)(x*)。因此,由法锥的定义,对于任意的y∈A(x*),〈-λz*,y-x*〉≤0,即
〈z*,y-x*〉≥0,∀y∈A(x*)。
(7)
又由于z*∈∂F(x*,x*),则对于任意的y∈A(x*),
F(x*,y)≥F(x*,x*)+〈z*,y-x*〉。
(8)
结合(7)式和(8)式,对于任意的y∈A(x*),F(x*,y)≥0,即x*是QEP(F,A)的一个解。
必要性:假设x*∈Sol(F,A)。令y*=ΨA(x*)(x*),则y*是问题(6)的一个解,则0∈λ∂F(x*,y*)+y*-x*+NA(x*)(y*),则存在z*∈∂F(x*,y*),使得0∈λz*+y*-x*+NA(x*)(y*)。因此,〈z*,x*-y*〉≤F(x*,x*)-F(x*,y*),且由法锥的定义,对于任意的y∈A(x*),〈x*-y*-λz*,y-y*〉≤0。因为x*∈A(x*),令y=x*,可得‖x*-y*‖2-〈λz*,x*-y*〉=〈x*-y*-λz*,x*-y*〉≤0,即‖x*-y*‖2≤〈λz*,x*-y*〉≤λF(x*,x*)-λF(x*,y*),因为x*∈Sol(F,A),所以x*∈A(x*),F(x*,y*)≥0。又因为F(x*,x*)=0,所以‖x*-y*‖2≤0,因此x*=y*=ΨA(x*)(x*)。
备注2 如果F(x,y)=〈f(x),y-x〉,其中,f:Rn→Rn是一个映射,则(6)式变为

=PA(x*)(x-λf(x))。
当F为强伪单调时,本文给出了它有唯一解的充分条件,结果如下:
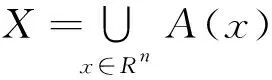
(i)存在k>0,使得
‖ΨA(x1)(x)-ΨA(x2)(x)‖≤k‖x1-x2‖,∀x1,x2,x∈X;
(9)
(ii)存在γ>0,使得对所有的x∈X,F在A(x)上是关于系数γ强伪单调的。
此外,如果
(10)
那么拟均衡问题QEP(F,A)就有唯一解。
证明固定x∈Rn,考虑如下均衡问题:找到x*∈A(x),使得
F(x*,y)≥0,∀y∈A(x)。
(11)
由于F是A(x)上关于系数γ>0的强伪单调映射,显然(11)式有唯一解(见文献[10])。因此,可以定义一个映射S(z)=z*,∀z∈Rn,其中S:Rn→Rn,z*是(11)的唯一解,即对于任意x∈Rn,S(x)是A(x)中唯一点使得下式成立:
F(S(x),y)≥0,∀y∈A(x)。
显然拟均衡问题(1)等价于映射S的不动点问题。下面证明若映射S是压缩映射,则拟均衡问题(1)有唯一解。对于任意x1,x2∈Rn,由命题1有S(x1)=ΨA(x1)(S(x1)),S(x2)=ΨA(x2)(S(x2))。令y2=ΨA(x2)(S(x1))。由(6)可得0∈λ∂F(S(x1),y2)+y2-S(x1)+NA(x2)(y2),则存在z*∈∂F(S(x1),y2),使得0∈λz*+y2-S(x1)+NA(x2)(y2)。
因此,由法锥的定义,对于任意y∈A(x2),〈S(x1)-y2-λz*,y-y2〉≤0,即〈S(x1)-y2,y-y2〉≤〈λz*,y-y2〉。由于z*∈∂F(S(x1),y2),则对于任意的y∈A(x2),F(S(x1),y)≥F(S(x1),y2)+〈z*,y-y2〉,即λF(S(x1),y)≥λF(S(x1),y2)+〈λz*,y-y2〉。从而,λF(S(x1),y)≥λF(S(x1),y2)+〈S(x1)-y2,y-y2〉。又由于S(x2)∈A(x2),则在上式中令y=S(x2),可得
〈S(x1)-y2,S(x2)-y2〉≤λ(F(S(x1),S(x2))-F(S(x1),y2))。
(12)
因为S(x2)=ΨA(x2)(S(x2))和y2=ΨA(x2)(S(x1)),所以y2∈A(x2),由命题1可得F(S(x2),y2)≥0,由于F是关于系数γ强伪单调的,有
F(y2,S(x2))≤-γ‖S(x2)-y2‖2。
(13)
又因为F是Lipschitz连续映射,由(2)(12)(13)式可得
2〈S(x1)-y2,S(x2)-y2〉≤2λ(F(S(x1),S(x2))-F(S(x1),y2))
≤2λF(y2,S(x2))+2λL‖S(x1)-y2‖‖S(x2)-y2‖
≤-2λγ‖S(x2)-y2‖2+2λL‖S(x1)-y2‖‖S(x2)-y2‖
≤-2λγ‖S(x2)-y2‖2+λ2L2‖S(x1)-y2‖2+‖S(x2)-y2‖2
≤-2λγ‖[S(x2)-S(x1)]-[y2-S(x1)]‖2+λ2L2‖S(x1)-y2‖2+
‖S(x2)-S(x1)‖2+‖S(x1)-y2‖2+2〈S(x2)-S(x1),S(x1)-y2〉,
由此可得
2〈S(x1)-y2,S(x2)-y2〉≤-λγ‖S(x1)-S(x2)‖2+2λγ‖S(x1)-y2‖2+λ2L2‖S(x1)-y2‖2+
‖S(x2)-S(x1)‖2+‖S(x1)-y2‖2+2〈S(x2)-S(x1),S(x1)-y2〉。
因此,
(λγ-1)‖S(x1)-S(x2)‖2≤(λ2L2+2λγ-1)‖S(x1)-y2‖2。
(14)
又
‖S(x1)-y2‖=‖ΨA(x1)(S(x1))-ΨA(x2)(S(x1))‖≤k‖x1-x2‖,
由(14)式可得
(λγ-1)‖S(x1)-S(x2)‖2≤k2(λ2L2+2λγ-1)‖x1-x2‖2。
(15)
(16)
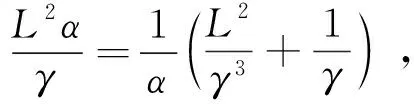

备注3 定理1将文献[9]中关于强伪单调拟变分不等式解唯一性充分条件的证明方法进行了拓展,推广到了更具一般形式的拟均衡问题中,证明了在强伪单调性和Lipschitz连续性的假设下拟均衡问题解唯一的充分条件。
3 不动点式动力系统
要确定本文的主要结果,需要回顾一下一般动力系统均衡点稳定性的概念
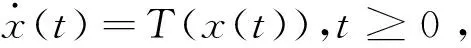
(17)
其中T:Rn→Rn为连续映射,x:[0,+∞)→Rn,t→x(t)。

‖x(t)-x*‖≤μ‖x(0)-x*‖e-ηt,∀t≥0。
(18)
此外,如果(18)式对于(17)式的所有解x(t)成立,则x(t)全局指数稳定。
为了求解拟均衡问题QEP(F,A),考虑如下形式的动力系统
(19)
式中,ρ>0。

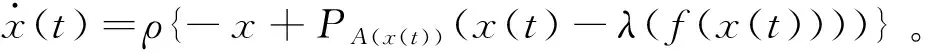
若定理1中的条件都满足,拟均衡问题QEP(F,A)就有唯一解。由命题1可知,x*是ΨA(x)的不动点。根据动力系统(19)的定义形式可知,x*是它的唯一均衡解。
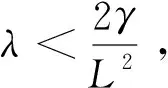
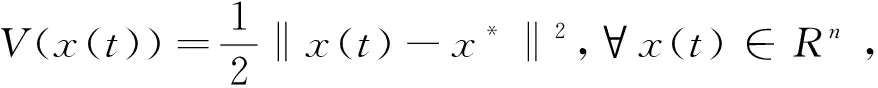

=ρ〈x(t)-x*,ΨA(x(t))(x(t))-x(t)〉
=ρ[〈x(t)-x*,ΨA(x(t))(x(t))-x*〉-‖x(t)-x*‖2]。
由Cauchy-Schwarz不等式和参考文献[10]命题3.1可得
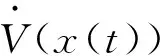
=-κ‖x(t)-x*‖2,