考虑非平稳横风作用的列车-大跨斜拉桥耦合系统动力响应

何旭辉，谭凌飞，顾建华，敬海泉†，李书昌

（1.中南大学土木工程学院，湖南长沙 410075；2.高速铁路建造技术国家工程实验室，湖南长沙 410075；3.广东广珠城际轨道交通有限责任公司，广东广州 510335）

截至2020 年底，我国高铁运营里程达3.79 万km，成为世界上高速铁路里程最长、列车密度最高、网络结构最复杂的国家.众所周知，高速铁路有着高平顺性、高舒适性、高稳定性和高安全性的要求，现代大跨度斜拉桥正朝着更大跨、更轻柔、更纤细的方向发展，因此当较大的铁路荷载作用在柔性的大跨斜拉桥上时，列车的行车安全性、舒适性和桥梁的安全性成为当下的热点问题［1］.此外由于长三角、珠三角地区处在太平洋台风的直接侵袭范围，与常规的风相比，台风的风速更大，非平稳特性更显著，因此台风的到来会对高速列车安全产生更不利的影响，高速列车的行车安全性将遭遇更大的挑战.

国内外学者已经对风-车-桥系统耦合振动开展了大量研究［2］，夏禾等［3］提出了一种基于Monte Carlo技术模拟随机风速场下列车-桥梁系统动力可靠性的分析方法.郭向荣等［4］考虑脉动风沿桥梁纵向的空间相关性，随机模拟出沿桥跨若干点处的风速时程曲线，采用时域分析法对脉动风作用下高速列车通过该桥时的车桥时变系统动力响应进行较详细的分析，从安全性与舒适性两方面计算分析该桥列车行车的临界风速.李永乐等［5-6］利用自制的气动力分离装置-交叉滑槽系统在风洞试验中研究了车辆和桥梁之间的气动影响，使用自编程技术建立了风-车-桥非线性空间耦合振动分析模型.韩艳等［7］研究车桥间气动干扰对桥上车辆行驶的影响，研究结果表明：考虑车桥间气动干扰对车辆动力响应影响较大.Montenegro 等［8］使用欧洲标准化委员会（CEN）离散阵风模型和基于随机生成风场的湍流风模型模拟生成了两种不同风模型，研究了不同风模型对列车侧风稳定性的影响.

上述风-车-桥系统耦合振动的研究多将风视为平稳随机过程，因此没有对非平稳风作用下的列车-桥梁振动进行研究.由于缺乏理论分析框架，对风-车-桥非平稳耦合振动的研究报道相当少见.然而，大多数列车倾覆事故实际上是由于重要的非平稳因素相关的极端风造成的［9］.与静止边界层风相比，非平稳极端风的风速呈现出时变均值、时变方差、时变频率等时变特征［10-11］.此外，在相对较短的持续时间内，这些极端事件中的风速可以达到平均值的数倍［12］.何旭辉等［13］基于伪激振法（PEM），建立了非平稳风作用下高速列车-桥梁耦合振动的有效分析框架，证明了风的非平稳特性对列车-桥梁耦合作用系统的动力性能有重要影响，其不足之处在于没有考虑真实的轮轨关系.因此，研究非平稳特性对车桥系统振动的影响具有重要意义.

本文的研究背景是在建的金海特大桥，该桥是主跨为3×340 m的四塔斜拉桥，也是世界上首座公路铁路两用的四塔斜拉桥，桥址靠近南海，所处的风环境十分恶劣，常年遭受台风侵袭，因此，开展非平稳风作用下大跨度斜拉桥桥上行车安全研究是十分有必要的.本文通过EMD（Empirical Mode Decomposi⁃tion）方法从已有的实测台风数据中提取出时变平均风速，将风谱中的平均风速替换成时变平均风速，通过谐波合成法模拟得到非平稳风脉动风速，将列车和桥梁的风荷载时程施加到由有限元分析软件ANSYS和多体动力学软件SIMPACK 联合建立的风-高速列车-大跨斜拉桥耦合分析模型当中，计算分析了平稳风与非平稳风作用下车桥系统的动力响应区别.

1 非平稳风场模拟方法

1.1 非平稳风速模型

在平稳风速模型研究中，在某一时刻t的风速等于平均风速加上均值为零的平稳脉动风速，即

式中：U(t)为t时刻的风速；U为t时刻的平均风速；u(t)为t时刻的脉动风速.

实测台风结果表明：不同于平稳边界层风速，台风风速时常在均值、方差、频率等方面表现出明显的时变特征.目前国内外学者提出了一些非平稳模型来描述台风和极端风的非平稳性，并与对台风或其他极端风的非平稳风速认识基本保持一致，即非平稳风速等于时变平均风速加上脉动风速，可表示为：

1.2 非平稳风场模拟

在进行风场模拟时，十分关键的一步就是对平均风剖面模型的研究.根据已有研究结果，针对地表粗糙度较小的状况，本文中选用拟合效果较好的指数函数模型来描述台风平均风速随高度的变化规律.指数函数风剖面经验模型见式（3）.

式中：Uz是高度z处的平均风速；Uz1是高度z1处的平均风速；α为地表粗糙度系数.

根据公式（2）可知，模拟非平稳风速需要分时变平均风速模拟和脉动风速模拟，然后再将这两部分叠加即可得到模拟出来的非平稳风速，图1 所示为模拟流程图.

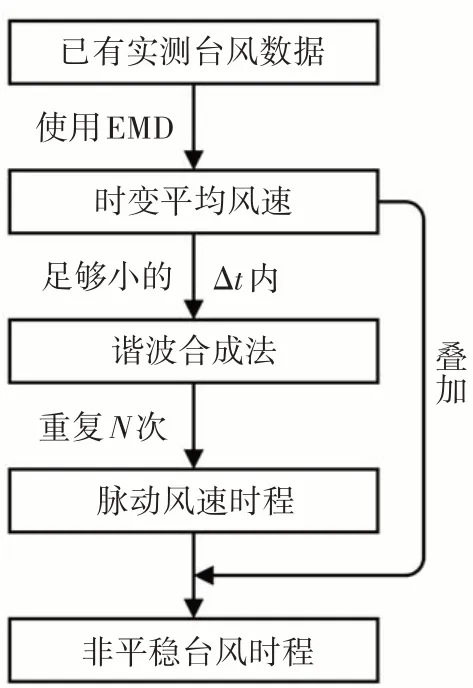
图1 非平稳风模拟流程图Fig.1 Flow chart of non-stationary wind simulation

现有研究中，一般采用三种方法来获取时变平均风速，分别是：①假定时变平均风速服从已知函数，如余弦函数；②从实际台风风速时程曲线中提取；③假定时变平均风速为一常数.因为台风的非平稳特性十分明显，风速变化很快，不同台风之间的物理特性相差较大，风速分布规律差别也较大，所以选用某一常数或服从某确定函数曲线的假定来模拟时变平均风速是不恰当的，因此本文使用EMD 分解方法从实测的台风风速时程曲线提取时变平均风速，这样可信度高且准确度也高.

平稳风的脉动风速通常基于经典功率谱，使用谐波合成法进行模拟.由于台风风速的非平稳性明显，风速变化快，其平均速度也表现出较明显的时变性，而传统谐波合成法的平均风速为常量，基于进化谱的理念，在模拟台风脉动风速时，通过时变平均风速的变化来实现更新功率谱，从而实现对台风的模拟［14］.将台风风场模拟时长T分成N个足够小的时间间隔∆t，T=N∆t，在足够小的时间间隔∆t内任意时刻的风速可视为该∆t内的平均风速，也就是时变平均风速等于平均风速.因此在模拟台风时需要分两步：①在每个足够短的时间间隔∆t内，采用谐波合成法模拟零均值稳态脉动风速，实现每个足够短的时间间隔∆t内的脉动风模拟；②在不同时间间隔中，随着时变平均风速变化更新风功率谱，实现不同时间间隔内的脉动风速模拟.

1.2.1 时间间隔∆t内的脉动风速模拟

直接采用谐波合成法对足够小的时间间隔∆t内的脉动风速进行模拟，以高度为z处的节点i(i=1，2，…，m)进行说明，具体步骤如下.

在模拟台风风场时，已有研究中，在水平顺风向一般选用经典风谱中的Kaimal谱作为功率谱密度函数，表达式如式（4）所示.

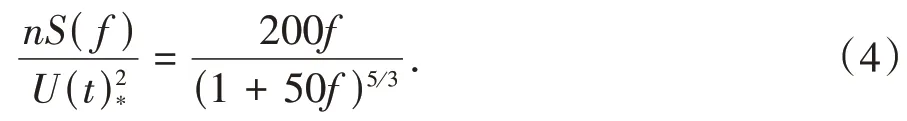
式中：S(f)为功率谱密度为相似率坐标，Uz(t)为时间间隔∆t内高度z处的时变平均风速；为时变摩擦风速，k=0.4，z0为地面粗糙度.

作用在桥梁节点上的脉动风速在空间上存在相干性，本文采用Davenport 形式的相干函数来表示这种相干性，表达式如下：

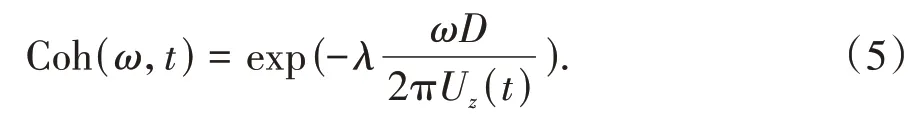
式中：ω为圆频率；D表示计算点之间的空间距离；λ为衰减系数，取7.

在模拟风场的横风向和竖风向时，只需要更换对应的风谱即可.

根据Shinozuka-Deodatis 理论，时间间隔∆t内的各个模拟点的脉动风速时程为：

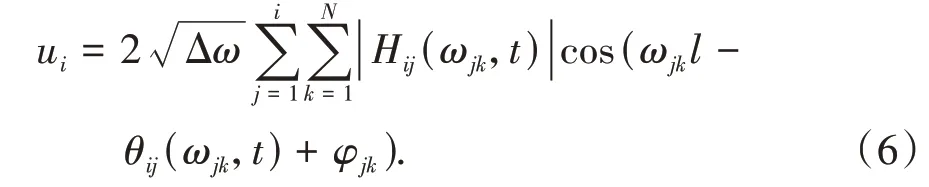
式中：N为一充分大的正整数；为频率增量，ωup为截止圆频率；φjk为随机相位角，均匀分布在(0，2π) 之间；ωjk为双索引频率进行Cholesky 分解所得矩阵H(ωjk，t)中的元素；θij(ωjk，t)为Hij(ωjk，t)的复角，即

1.2.2 不同时间间隔内的脉动风速模拟

接着只需将式（4）中的功率谱更新，再重复第一步，就能获得每个时间间隔内的脉动风速.最后将脉动风速与时变平均风速相加就可获得非平稳风速.

2 风-列车-大跨斜拉桥耦合系统

2.1 作用在列车和桥梁上的非平稳风荷载

由数值模拟方法得到非平稳风场后，作用在列车和桥梁上的风荷载分为两部分：一是由时变平均风引起的时变静风荷载；二是由脉动风引起的非平稳抖振力.由Davenport 准定常理论可得，主梁和列车在时变平均风作用下的非平稳静风荷载可表示为：

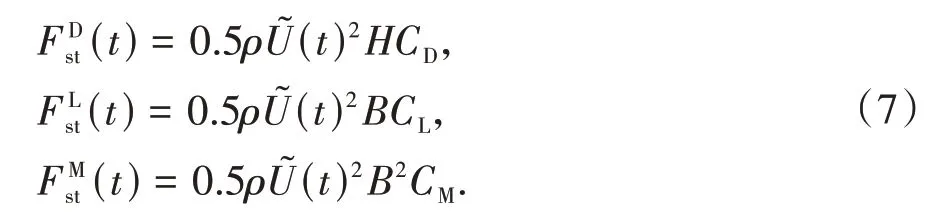
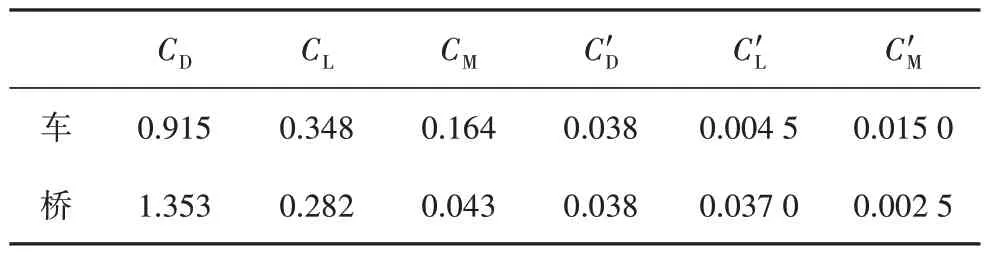
表1 车-桥系统中列车与桥梁空气动力学参数Tab.1 Aerodynamic parameters of train and bridge in vehicle-bridge system

抖振力载荷是由随机风的脉动量引起的.根据准定常假定，主梁的抖振力载荷根据公式（8）计算.

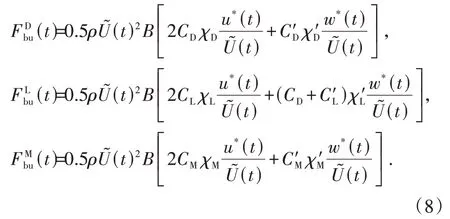
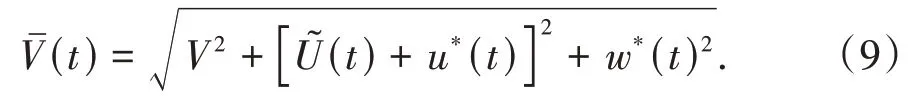
式中：V为列车运行速度.

2.2 列车动力学模型

ICE3 型列车模型在SIMPACK 软件中建立，列车的具体参数见文献［15］，单节列车模型为二系悬挂四轴列车，包含4 个轮对、2 个转向架和1 个车体，各个刚体通过弹簧和阻尼连接，共7 个刚体，在软件中列车模型如图2 所示.悬挂系统分为一系悬挂、二系悬挂，一系悬挂由轴箱弹簧、轴箱减震器等组成，用于转向架与轮对之间的连接；二系悬挂主要由空气弹簧、横向减振器、抗蛇行减振器等组成，用于车体与转向架之间的连接.为确保建立的列车运动接近现实情况，各个刚体均考虑6 个自由度，其中各个自由度分别为伸缩、横摆、浮沉、侧滚、点头、摇头，因此单节列车一共42个自由度.

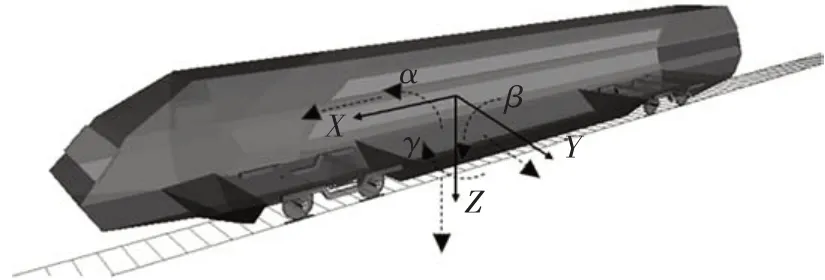
图2 SIMPACK中列车模型示意图Fig.2 Diagram of train model in SIMPACK

2.3 桥梁、轨道结构动力模型

本文使用的桥梁为在建的金海特大桥，为多塔多跨斜拉桥，全长1 369 m，跨径布置为（58.5+116+3×340+116+58.5）m，主箱采用单箱三室截面，顶板采用正交异性钢桥面板，主梁断面高度4.5 m，桥面总宽49.6 m，中间钢箱梁宽17.6 m，两侧挑臂式桥面宽16 m，整体布置图如图3所示.大跨度斜拉桥和轨道有限元模型均使用有限元分析软件ANSYS 建立，桥梁前10 阶频率见表2.对建立好的模型进行子结构分析，得到所需的刚度矩阵和质量矩阵，通过ANSYS 与SIMPACK 之间的程序接口，最终以柔性体和柔性轨道的形式分别建立斜拉桥和轨道的动力分析模型，并使用扣件将轨道与主梁连接起来，通过弹簧-阻尼来模拟扣件.根据我国《高速实验列车技术条件》中的建议，计算时采用德国轨道低干扰谱模拟不平顺功率谱，空间步长为0.2 m.本文列车采用单列8车编组（拖车+6动车+拖车）的高速列车模型，为了避免由于弹性轨道体过短而导致列车上桥、下桥瞬间动力响应发生突变，轨道模型分为3 部分：桥前轨道模型（长度216 m）、桥上轨道模型和桥后轨道模型（长度216 m）.

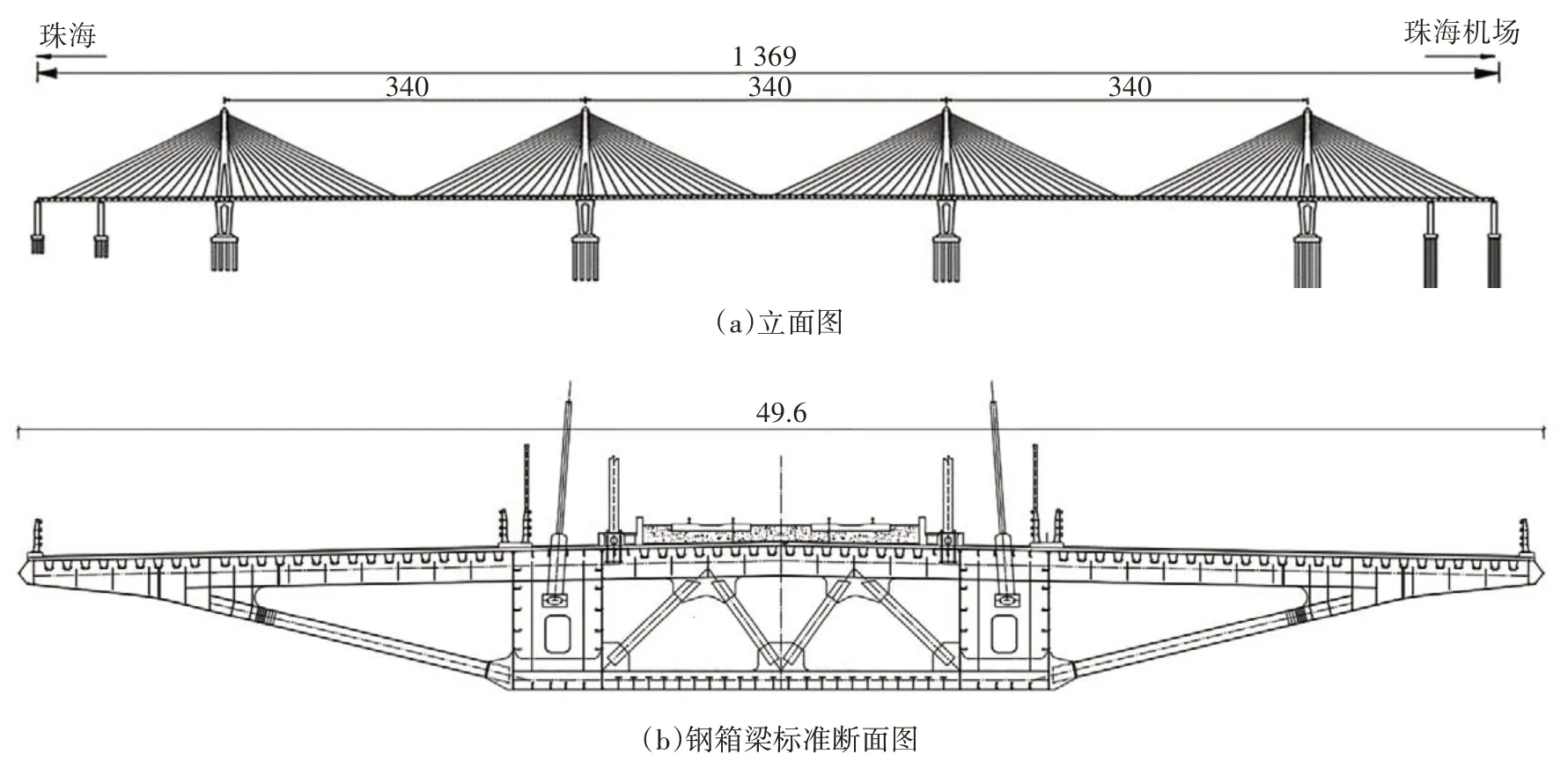
图3 金海特大桥的整体布置图（单位：m）Fig.3 Overall layout of Jinhai Bridge（unit：m）

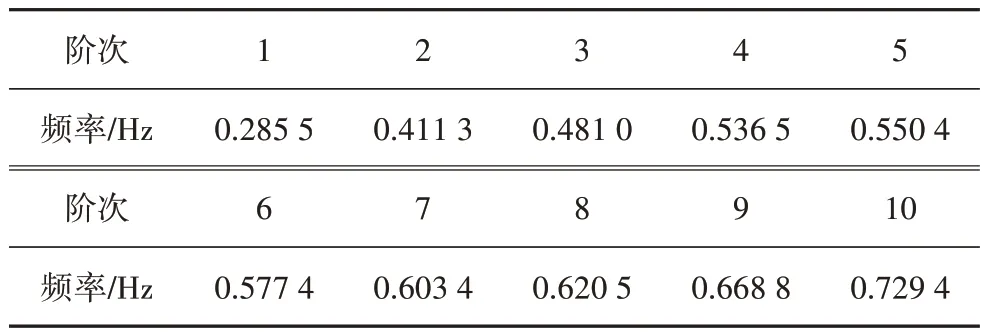
表2 桥梁的前10阶动力特性Tab.2 Dynamic characteristics of the first 10 modes for bridge

2.4 车-轨-桥耦合模型验证

为验证本文建模方法的正确性，采用文献［16］中的桥梁、轨道和列车参数，利用本文中的轮轨耦合方法建立车−轨道−桥耦合振动分析模型［17］，计算了1节拖车以300 km/h通过桥梁时，桥梁跨中和钢轨跨中的竖向位移.文献［16］中也验证了SIMPACK 与ANSYS 仿真分析的正确性.将本文计算结果与文献［16］和文献［17］对比，如表3 所示，结果吻合较好，误差在3%以内，可以证明本文计算结果的准确性.

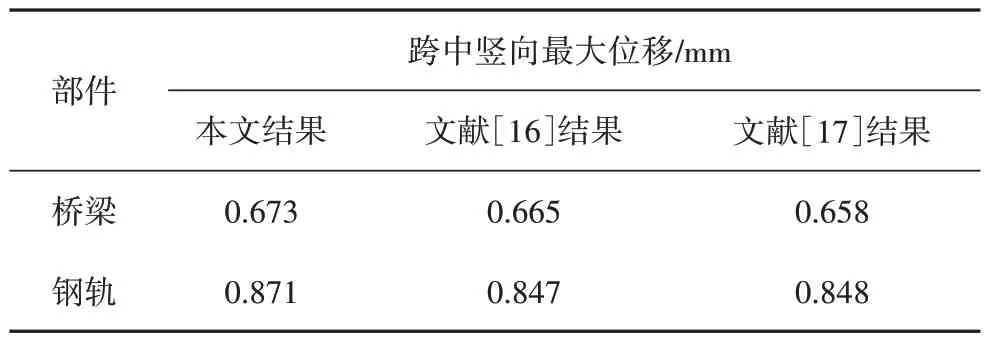
表3 计算结果对比Tab.3 Comparison of calculation results

3 非平稳风对列车-大跨斜拉桥耦合系统动力响应影响分析

本文对现有实测台风数据采用上述风场模拟方法获得了非平稳台风风速时程，另外采用谐波合成法模拟得到平稳风速时程，图4给出了时距为10 min的非平稳风在顺风向的时程曲线.对第一个模拟点的非平稳风速脉动部分进行快速傅里叶变换（FFT），并与Kaimal 谱进行比较，得到顺风向脉动风速功率谱密度如图5所示.

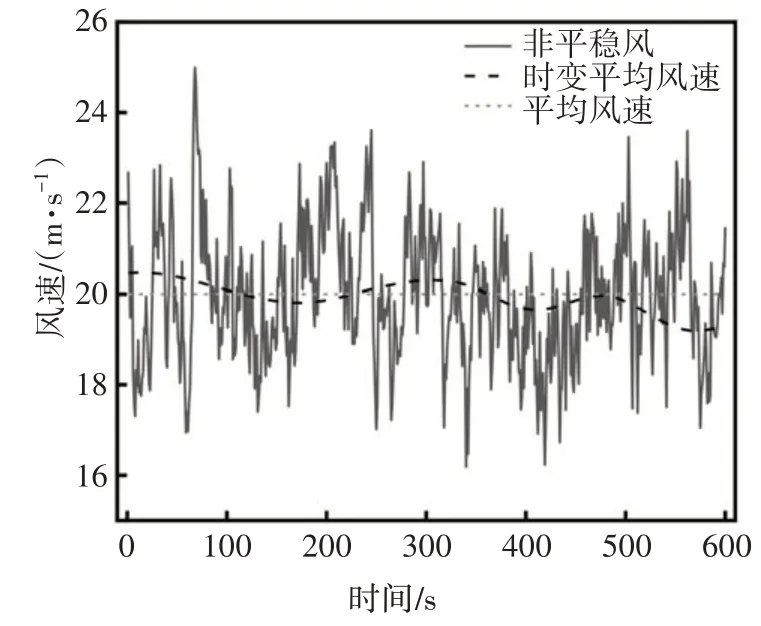
图4 风速时程曲线Fig.4 Time-history curve of wind speed

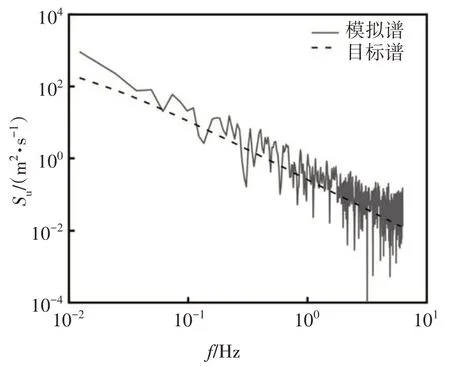
图5 顺风向脉动风速功率谱对比Fig.5 Comparison of power spectrum of longitudinal fluctuating wind speed

由图5 可知，模拟得到脉动风速的模拟功率谱与目标谱，除在最低频率部分外，吻合非常好.

3.1 非平稳风对列车动力响应影响分析

在轨道不平顺的激励下，经过桥梁时会产生振动，列车的振动通过轮轨传递至主梁上，导致大跨斜拉桥也发生振动，而大跨斜拉桥的振动又会通过轮轨传递到车体.对于列车而言，通常采用安全性和舒适性指标来反映其动力响应.本文分别计算非平稳风和平稳风对耦合系统动力响应的影响，列车舒适性指标主要考虑列车车体的加速度.为使结果更加直观，直接比较两种风环境下的车体加速度的时程曲线.由于拖车质量小、响应大，因此给出拖车在大跨斜拉桥上以300 km/h 的速度运行时两种风环境下的加速度时程曲线，结果如图6 所示.随后将加速度时程曲线进行快速傅里叶变换（FFT），得到加速度的频谱图，如图7所示.

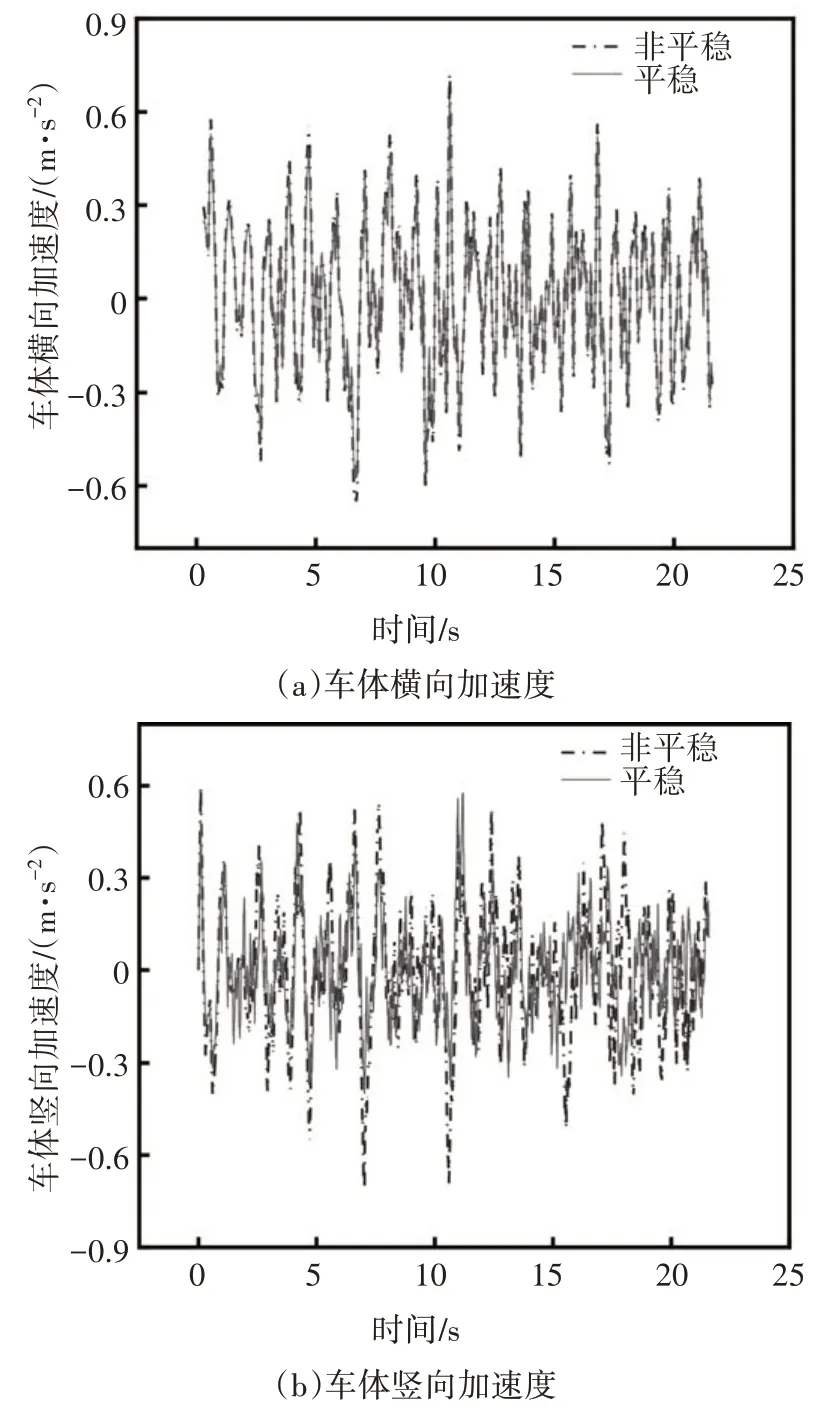
图6 列车车体加速度时程曲线比较图Fig.6 Comparison diagram of acceleration time history curve of train body

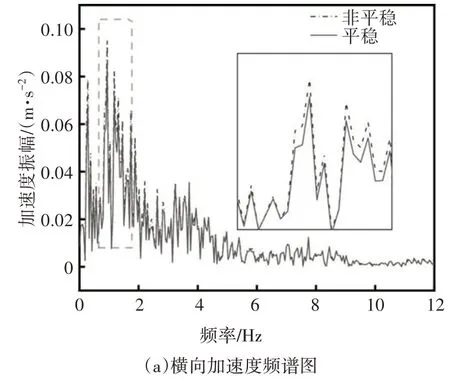
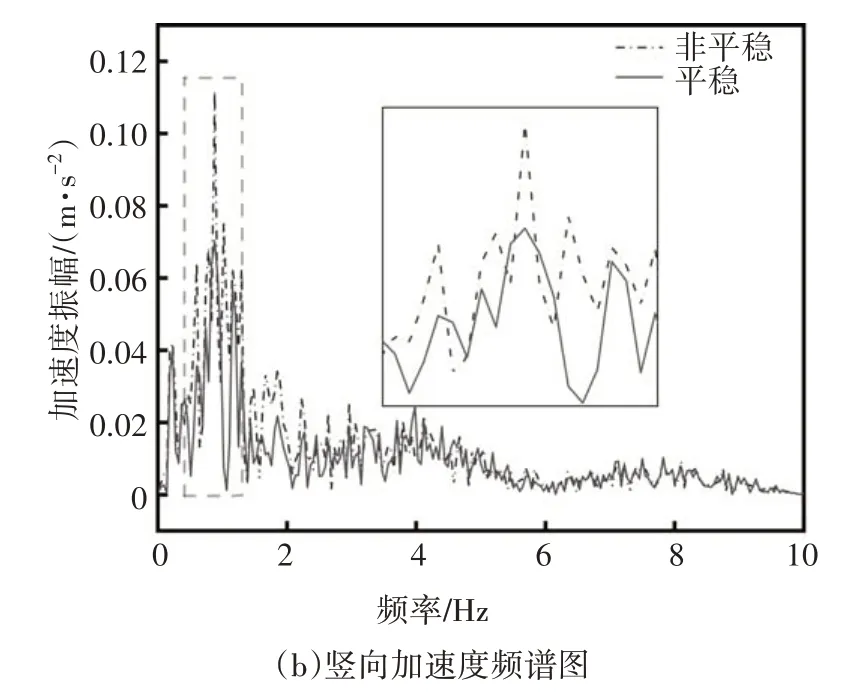
图7 列车车体加速度频谱图Fig.7 Spectrum diagram of acceleration of train body

由图6 可知，首先两种风环境下列车的加速度趋势基本一致，但加速度的峰值却有一定的差距.非平稳风与平稳风作用下桥上列车车体的最大横向加速度分别为0.923 m/s2和0.823 m/s2，增长幅度约为12%；而竖向加速度分别为0.712 m/s2和0.576 m/s2，增长幅度约为23%.这表明非平稳风作用下列车加速度的峰值会有一定的增加.在本文中列车横向和竖向最大加速度分别增加了0.1 m/s2和0.136 m/s2，而车体加速度属舒适性指标，因此非平稳风作用下会导致行车舒适性降低.

由图7 可知，车体横向加速度在非平稳风和平稳风作用下对应的一阶横向频率均为0.94 Hz，但非平稳风产生的振动在低频区域内比平稳风更加突出；而车体竖向加速度的情况也是相同的，它们的一阶竖向频率均为0.88 Hz，在低频区域内非平稳风引起的振动更加明显，因此非平稳风作用下列车的振动频率和平稳风作用下是相同的，但在低频范围内非平稳风引起车体的振动更加强烈.

本文列车行车的安全性指标主要包括：轮重减载率、轮轨横向力和脱轨系数.本文采用Sperling 指标来评价乘客乘车的舒适性.列车在大跨斜拉桥上以200～300 km/h行驶，受到非平稳风与平稳风作用，列车的安全性和舒适性指标如图8所示.

由图8 可知，安全性和舒适性指标均随着列车车速的增大而提高，其中轮重减载率在列车车速超过225 km/h 时就超过了规范限值，其他指标均在规范限值以内.当列车车速低于250 km/h时，非平稳风作用下，列车的安全性指标略有增大；当列车车速达到275 km/h 后，列车的轮重减载率和轮轨横向力表现出较大的差异，以车速300 km/h 为例，非平稳风作用下，列车的3 种安全性指标分别为0.905、75.1 kN和0.336，平稳风作用下的数值分别为0.827、73.3 kN和0.323，增幅分别约为9%、14%和4%，故非平稳风会使桥上行车的安全性更差.然而不同种类风作用下列车的竖向Sperling 指标没有明显变化，这是因为计算中风速的竖向分量大小相差很小；而非平稳风作用下车体横向Sperling指标有一定的增大.

图8 列车安全性和舒适性指标对比图Fig.8 Train safety and comfort index comparison chart

3.2 非平稳风对大跨斜拉桥动力响应影响分析

对于大跨斜拉桥而言，本文采用加速度来评价其动力响应.同样地先给出四塔斜拉桥中跨跨中处的加速度时程曲线，结果如图9 所示.同样地将主梁跨中加速度时程曲线进行快速傅里叶变换（FFT），得到加速度的频谱图，如图10所示.

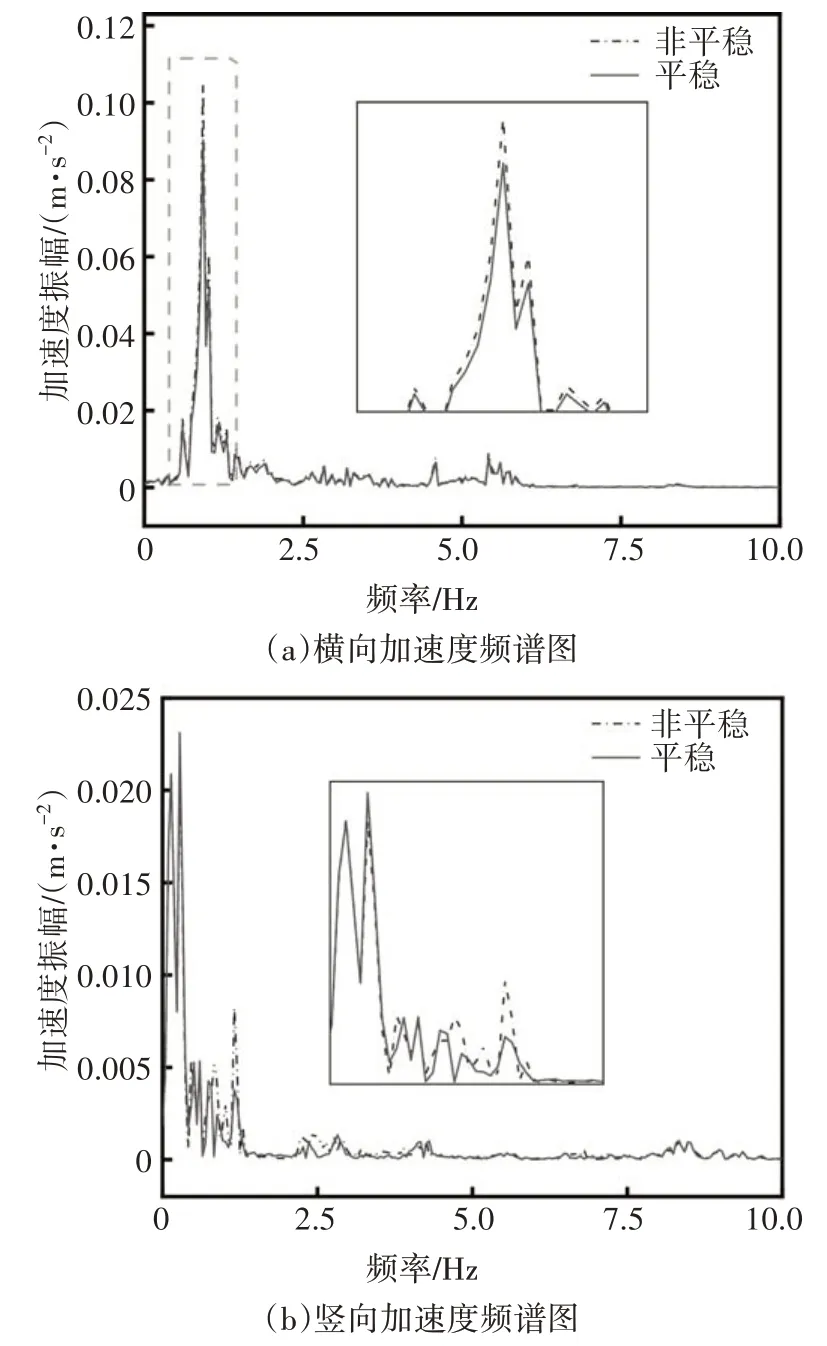
图10 桥梁跨中加速度频谱图Fig.10 Acceleration spectrum of bridge midspan

由图9 可知，两种风环境下桥梁的横向加速度曲线变化趋势基本保持一致，非平稳风对应的变化幅度更大且最大横向加速度为0.344 m/s2，而平稳风对应的最大横向加速度为0.296 m/s2，变化幅度约为16%；而在竖向最大加速度方面，非平稳风和平稳风作用下分别为0.176 m/s2和0.165 m/s2，变化幅度约为7%，因此非平稳风会增大桥梁加速度.

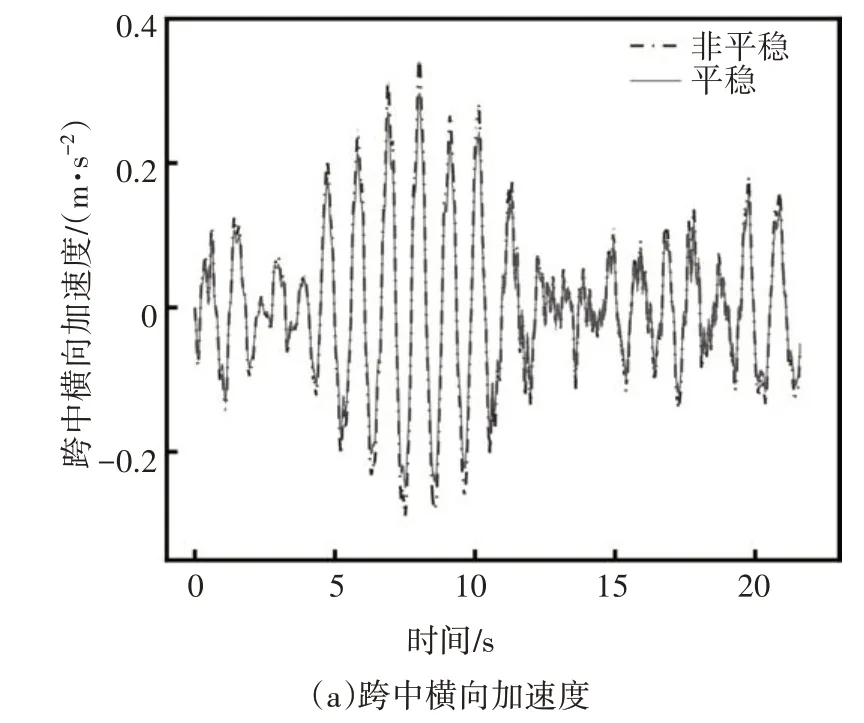
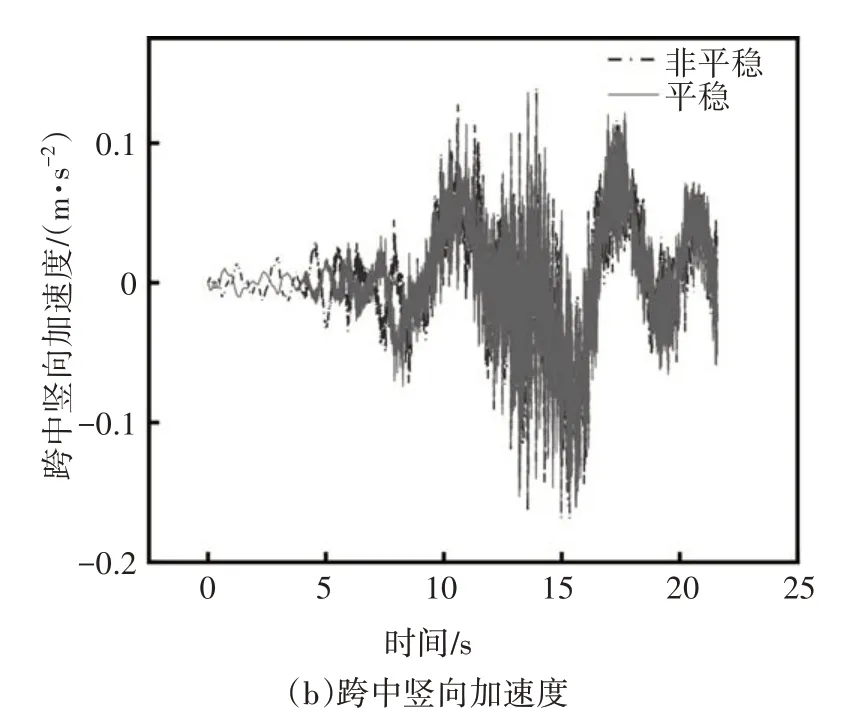
图9 主梁1/2跨中加速度时程曲线比较图Fig.9 Comparison diagram of acceleration time history curve in 1/2 span of main girder

由图10 可知，在低频区域内，对比平稳风，非平稳风对桥梁产生的横向振动更剧烈，而桥梁横向加速度在非平稳风和平稳风作用下桥梁的一阶横向频率为0.93 Hz，这和列车横向加速度的一阶横向频率0.94 Hz 十分接近，因此列车过桥时发生过车桥共振；在桥梁竖向加速度方面，两种风作用下桥梁的一阶竖向频率为0.28 Hz，这和桥梁自身的一阶对称竖弯频率0.285 5 Hz几乎完全一致，但在此频率处平稳风对桥梁产生的振动比非平稳风更大，而在高频区域内两种风没有明显区别.

4 结论

本文通过数值模拟技术模拟得到了非平稳台风风场，并建立了高速列车-大跨斜拉桥耦合振动分析模型，开展了非平稳风与平稳风作用下车-桥系统动力响应影响分析，所得主要结论如下：

1）对列车系统而言，在非平稳横风作用下，斜拉桥上运行的列车加速度会增大，经比较列车横向和竖向最大加速度增大幅度分别约为12%和23%，因此非平稳风横风作用下列车的行车舒适性会明显降低；通过频谱分析可以发现，非平稳风和平稳风作用下列车的一阶振动频率相同，但在低频范围内非平稳风对列车产生的振动更强烈；比较两种风环境下列车的安全性指标，非平稳台风会使列车的轮重减载率、轮轨横向力和脱轨系数增大，相比于平稳风，增长幅度分别约为9%、14%和4%，因此非平稳台风会使桥上行车的安全性更差；此外列车的Sperling 指标仅在横向表现了差异，在竖向没有表现出明显的差异.

2）对桥梁系统而言，在非平稳横风作用下，斜拉桥跨中处的加速度会增大，经比较可知，中跨跨中横向和竖向最大加速度增大幅度分别约为16%和7%；桥梁竖向加速度频谱图表明，在非平稳风和平稳风作用下桥梁和列车在横向的振动频率相同，两者可能发生共振；而竖向加速度频谱图显示，在低频区域内平稳风对桥梁引起的振动比非平稳风更加强烈，并且振动的频率刚好与桥梁本身的一阶对称竖弯基频接近.