非饱和流固耦合物质点方法(CMPM)的原理及应用

王斌，周傲，陆盟，王佳俊

（1.中国科学院岩土力学与工程国家重点实验室，湖北武汉 430071；2.湖北工业大学土木建筑与环境学院，湖北武汉 430068；3.同济大学土木工程学院，上海 200092；4.中国地质大学工程学院，湖北武汉 430074）

我国是滑坡灾害多发的国家，近年来，滑坡造成的年均死亡人数已连续多年超过1 000 人，滑坡灾害不仅给当地居民的生命财产造成极大损失，有的还严重影响铁路、公路、水运及水电站等基础设施的安全运营［1-4］.降雨一直是诱发滑坡灾害的一个重要因素，全国290 个县市地质灾害调查结果表明，滑坡在地质灾害中所占比例高达51%，而降雨诱发的滑坡比例竟达到滑坡总数的90%［5］.因此，准确描述与预测滑坡的运动过程及其致灾范围，对于滑坡灾害的防治具有重要的意义.

目前，对于滑坡运动过程的描述一般采用数值试验进行仿真模拟［6-7］.传统的有限元方法因为在处理大变形时，容易造成网格的奇异，雅可比矩阵出现负值，因此不能有效模拟坡体在产生初始破坏后的渐进大变形过程.相比之下，物质点方法（MPM）则通过使用拉格朗日以及欧拉两套网格，避免了有限元中由于大变形而出现的网格畸形问题［8］，同时，其计算精度及计算效率都比较高，因此，近年来在国内外受到了诸多研究者的推崇［9-12］.

目前，耦合的物质点方法主要可分为两种形式［13］：一种是基于v-p 格式，也就是以固体颗粒的速度和孔压作为未知量，这种格式的结构相对简单，但是不能考虑流体-固体间的相对速度；另一种则是基于v-w 格式，也就是以固体的速度以及流体的速度作为未知量，这种格式考虑更为全面，但是由于流体速度和固体速度同阶积分，使得程序的稳定性比较欠缺.Zhang 等［14］最先将物质点方法应用到孔隙介质分析中，但是由于针对流体、固体采用了同阶的积分形式，在考虑整体程序稳定性的前提下，这种方法仅能分析小变形问题，却牺牲了物质点在大变形分析中的优势和特点.Jassim 等人［15］则基于混合物理论提出了v-w 形式下的流固耦合方法，目前它也是物质点流固耦合方法中使用最为普遍的，它通过依次求解基于固体以及混合物的动量守恒方程，先后获得固体颗粒及流体颗粒的速度，并且通过高斯积分来提高应力计算精度，但是由于物质点在背景网格中的流动性，很难保证网格的质量和网格中的物质点的质量相等，因此质量难以保证守恒.Bandara和Soga［16］则基于混合物理论，推导了基于两套颗粒（一套表征固体，另一套则表征流体）的物质点流固耦合控制方程，并且通过引入B-bar型函数在物质点上直接求解孔压以防止出现应力自锁的现象，但是由于两套颗粒的使用，程序的稳定性以及计算效率都大幅降低.Yerro 等［17］则在随后的研究中又重新使用了一套颗粒，通过流体、固体之间的比例来确定每个颗粒的组分组成，并且进一步推导了在非饱和情况下液相-气相-固相的全耦合控制方程，但由于气相的引入，使得这种方法在较大（极端）变形的情况下会引起程序的不稳定，从而降低了方法的适用性.

本文基于连续介质力学的质量以及动量守恒原理，同样使用了一套颗粒，在考虑极端变形的情况下，通过引入饱和度简化考虑了非饱和土的力学行为，推导并提出了流固耦合物质点方法（CMPM），可求解流固耦合下岩土结构的极端变形问题.在构建这样一个流固耦合控制方程的时候，虽然使用饱和度简化考虑了气相，但在实用性上增加了程序的稳定性.另一方面，降雨滑坡问题则是一个典型的非饱和问题.因此，本文首先比较了经典的一维非饱和土渗流试验（Liakopoulos test），以及Terzaghi 一维固结试验（饱和度设置成1 的时候，程序即可从非饱和的情况退化为饱和的情况），以证明CMPM 在饱和/非饱和土力学行为模拟中的适用性，最后，进一步结合降雨滑坡算例，验证了方法在解决降雨诱发滑坡模拟问题中的可行性.

1 耦合物质点法

基于连续介质力学的质量以及动量守恒原理，本节针对基于速度场（v-w formulation）的物质点流固耦合系统控制方程进行了详细的推导.

1.1 控制方程

基于连续介质力学的质量以及动量守恒原理，任意连续体的系统控制方程可以表示为

式中：ρ是质量密度；v是速度；a是加速度；σ是对称应力张量；b是体力，比如重力.值得注意的是，这些变量都是物质点在空间及时间上的函数.辅以合适的本构方程来描述物质点之间的内部相互作用以及应变和位移之间的运动关系，同时给予相应的边界条件和初始条件，上述系统控制方程，可以通过解析方法或数值模型来求解.

1.1.1 土颗粒质量守恒

土颗粒的质量守恒方程为

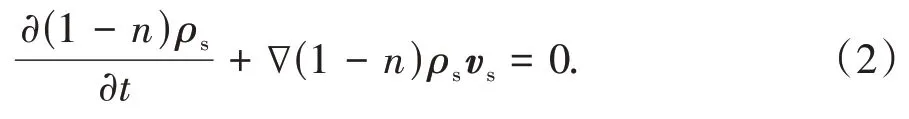
式中：n表示土体的孔隙率；ρs是土颗粒密度；t表示时间；vs为土颗粒的速度.

忽略土体孔隙率的空间梯度，并假设土颗粒骨架是不可压缩的，公式（2）可以简化为：

1.1.2 流体质量守恒

流体的质量守恒方程可以表示为：

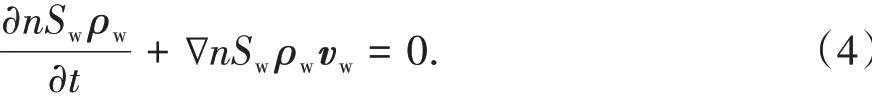
为行文方便，以下均用水来替代流体，以便和孔隙水压力等变量保持一致.式中，ρw表征水的密度；Sw为土体的饱和度；vw为水的速度.对公式（4）进行求导并展开如下：

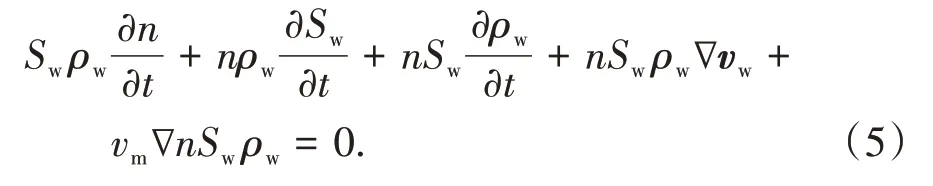
将公式（3）代入公式（5），并忽略流体密度的空间梯度，公式两边同时消去ρw，公式（5）可简化为

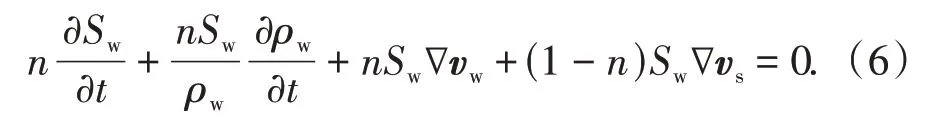
假设孔隙水压力的正压行为，即孔隙水压力的大小仅取决于水的密度，而同时水的密度变化也仅依赖于孔隙水压力的变化，因此，水密度的变化可以表示为孔隙水压力变化的函数：

式中：pw为孔隙水压力；Kw为水的体积模量，这里假设为常数.

另一方面，土体的饱和度Sw是土体吸力以及水力历史的函数，可以用土水特征曲线（SWRC）来表示，较为常见的可以采用Van Genuchten［18］公式来表达，即

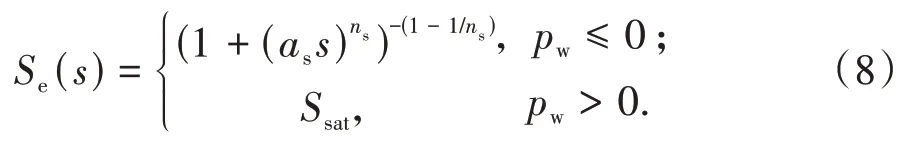
式中：as、ns是拟合参数.s为土体吸力，为气压pa与水压pw的差值，即s=pa-pw.为简单起见，在方程的推导中，不考虑气相，即pa为零，因此，土体的吸力在数值上可等效于负孔压，s=-pw.Se则为有效饱和度，可表示为：

式中：Sres和Ssat是土体干燥条件下的残余饱和度和充满水时的饱和度（在大多数情况下，其饱和度为1.0）.

因此，饱和度与时间的导数可以写为：

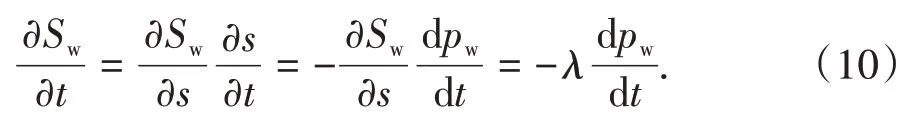
式中：λ等于∂Sw/∂s.

将公式（3）（7）（10）代入方程（6）中，在简单的代数运算之后，可以得到求解孔隙水压力的公式：

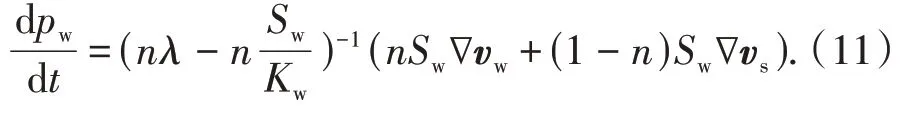
1.1.3 水的动量守恒

水的动量守恒方程如下：

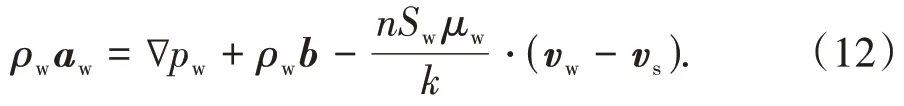
式中：aw为水的加速度；μw为水的黏滞系数，一般取为常数；k是土体的渗透性系数，其可以表示为土体饱和度的一个函数.可以利用土水特征曲线（SWRC）建立起土体的渗透性系数与饱和度之间的联系.而土体的实际渗透性系数通常可以表示为土体在饱和情况下的渗透性系数乘以一个相对渗透性系数，即

式中：krel即为相对渗透性系数，其是土体实际渗透性系数与完全饱和下土体的渗透性系数的一个比值，利用Van Genuchten公式，可以得到

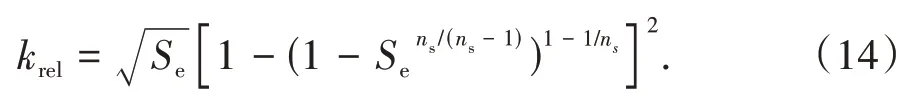
1.1.4 混合物的动量守恒

混合物的动量守恒方程可以表示为：

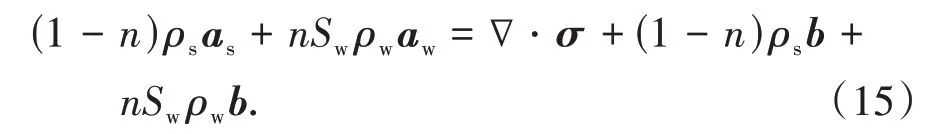
式中：as为土颗粒的加速度；σ为土体的总应力.考虑在非饱和状态下，土体的总应力利用Bishop 有效应力进行计算，即

式中：σ′为Bishop 有效应力.χ为基质吸力系数，从0到1 变化，涵盖从干燥到完全饱和条件下的土体.为方便起见，通常χ在计算中可简化为等于饱和度Sw.m为单位基向量，平面应变分析中，向量m=［1 1 0 1］T.同样，由于在方程的推导中忽略了气相，即pa为零，因此上式可简化为

1.1.5 土体颗粒骨架的孔隙率计算

基于变形梯度，在每个时间步长Δt之后，土体的孔隙率更新如下：

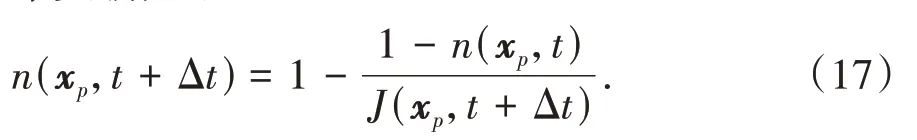
式中：J是表征变形梯度张量的雅可比值，在任一时间步长内，当变形足够小的时候，其可以通过应变张量的秩来表示，即J=1+tr(ε)，其中ε即为在该时间步长内的应变增量.

1.2 控制方程的弱形式

至此，基于速度场的流固耦合控制方程已经全部得出，即流体的动量守恒方程（公式（12）），以及混合物的动量守恒方程（公式（15））.在相应的公式中，两边同时乘以加权函数wh，并在相应积分区域进行积分即可得到动量平衡方程的弱形式.

采用分部积分，将应力项展开，并结合散度定理，水的动量平衡方程为

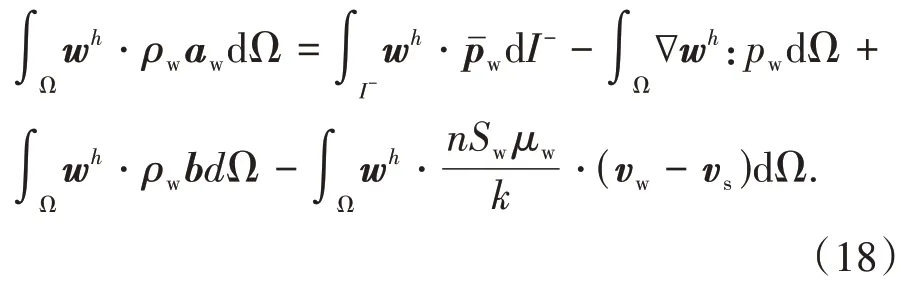
同理，可得到混合物的动量平衡方程

式中：aw、as分别为水和土体颗粒的加速度；Ω为积分区域；I-为积分区域的边界；τ 和则分别是边界上设定的应力和孔隙水压力，结合柯西边界条件，其分别可以表示为

式中：n为边界上的方向函数.

1.3 控制方程的离散化

不同于有限元方法，应力应变选择在高斯点上进行积分，物质点法中通常直接在物质点上进行积分.为描述清晰，物质点方法离散示意图如图1 所示，其中上标“0”表示连续体初始状态，“1”表示变形后状态.物质点用于表征结构本身，储存和结构本身相关的一切信息以及状态变量；背景（欧拉）网格仅用于求解控制方程，网格节点信息不进行存储.通过背景网格上的形函数，物质点上的信息与节点上的信息可以直观地联系起来，构造于积分区域上的控制方程也就可以转化为物质点上信息的求和.

图1 物质点方法示意图Fig.1 Material point method diagram

以物质点质量mp求解为例，物质点方法将原始构形中的连续体分解成Np个材料点集合，同时认为，每个物质点在空间上占据有相应的体积区域，但不一定需要明确具体的形状，在对应区域内，存在质量，而在区域外，质量即为零.因此，任一物质点的质量即可表达为连续体的空间密度在其相应区域上的积分，即

式中：Vp即为物质点p所对应区域的体积；δ即为狄拉克（Dirac delta）函数对式（21）两边进行求和，整个连续体的质量即为

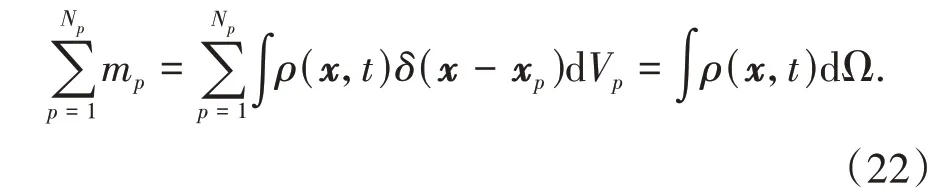
对比公式（22）以及控制方程（18）和（19），方程中的其他积分项同样可以相应转化为物质点上信息的求和.为方便起见，下文首先给出公式（18）及（19）离散后最终的矩阵形式，再逐一介绍每项的具体形式.

控制方程的矩阵形式可以转化为

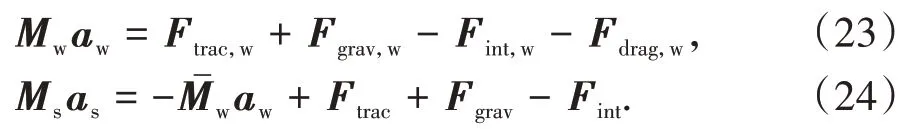
式中：M为质量矩阵，同有限元类似，将所有含有物质点的单元逐一组装起来，即

式中：nels 即为包含了物质点的单元数目，下标α分别代表w、s，即流体项和固体项.在实际应用过程中，为了减少计算量，尤其是在显示计算中，通常将质量矩阵对角化：

在上述矩阵中，ne是每个单元的节点数，而每个对角项也对应于每一个节点i.在平面应变问题中，每个节点对应的质量矩阵可以写为

式中：mα，i表示在相应单元内，所有物质点向节点i投影得到的节点质量，即

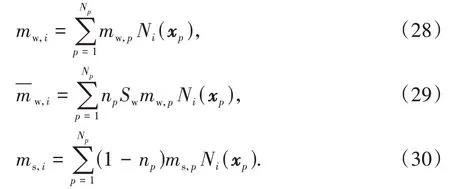
式中：np表示在物质点p处土体的孔隙率；mw，p、ms，p分别是水和土颗粒的质量；Np是一个单元内物质点的数量；Ni（xp）是第i个节点上的形函数在xp位置上的取值.为了行文简单，以下其余的变量仅从单元的角度来介绍如何进行离散.

Fgrav，w和Fgrav分别是指水的重力，以及水和土体颗粒的总重力，可分别表示为

式中：

式中：Vp为物质点p的体积；g是重力加速度，近似表示为g=（0.0，-10.0）T.

边界节点的作用力施加则是首先将作用力施加到位于边界附近的物质点上，利用背景网格上的插值函数，再映射到节点得到边界作用力.因此，将边界物质点上的节点力以及水压力向单元边界进行映射，得到边界上的总节点力Ftrac，和水压力Ftrac，w.

式中：Nblp是边界附近物质点的数量.

内力Fint以及由于水压力作用引起的内力Fint，w分别为

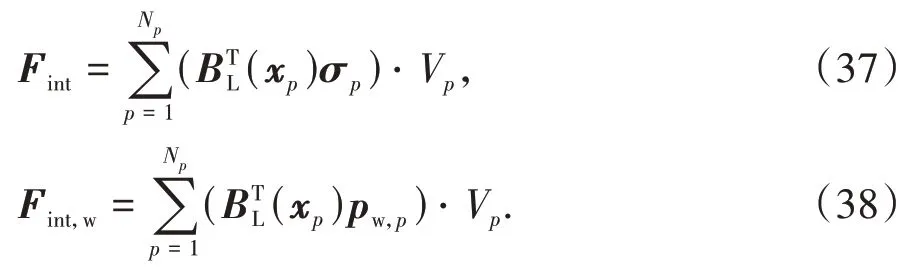
式中：pw，p和σp分别是作用在物质点上的水压力和总应力；B矩阵为基本的单元应变位移转换矩阵，不赘述.

土颗粒骨架与水之间的相互作用则可通过一种相互之间的胶结力Fdrag来表达，它与土颗粒与水相互之间的速度差成正比，即

式中：Q为一对角矩阵，对角线上的每个节点i对应的值qi由下式给出：

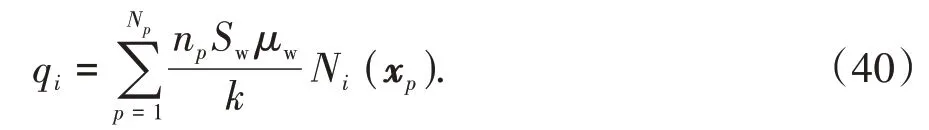
值得注意的是，饱和状态下的流固耦合控制方程，其原理与非饱和情况下的推导计算过程大体相同，只需将饱和度设置为1，控制方程即可直观地退化成饱和状态下的动量守恒方程.这里不做详细介绍，可留给读者做简要推导.

1.4 耦合物质点方法(CMPM)的计算步骤

为了求解控制方程，不仅在空间上需要对公式（23）（24）进行离散，同时也需要对其在时间维度上进行离散.因为将质量矩阵离散为对角形式，其在存储时就可存储为向量的形式.于是，在整个控制方程求解时，避免了大型的矩阵运算，可以通过向量运算直接求解，而在时间上的迭代则选择了中心点插值的显示积分形式.

相比较于有限元分析中更广泛使用的v-p 格式，耦合物质点方法采用了基于速度场的v-w 格式，其有两个优点：1）积分过程中，时间步长的选择更为宽松［17］，可以提高计算效率，节省计算时间；2）避免了大型矩阵运算，求解过程更为直接.综合起来，耦合物质点方法算法步骤总结如下.

1）将储存在物质点上的信息映射到背景网格上，初始化节点上所有变量.

2）求解流体（水）相的加速度，见公式（23）.

3）求解固相的加速度，见公式（24）.

4）更新节点上流、固两项的速度.

5）更新物质点上流、固两相的速度，然后根据计算得出的速度更新物质点的位置.

6）基于物质点上新的速度，返回映射更新节点上的速度，基于速度梯度，计算物质点上的应力和水压力.

7）重置背景网格，开始下一个计算周期.

2 数值算例

2.1 一维固结试验

图2（a）给出了一维固结试验示意图，砂柱高1 m、宽0.1 m，处于完全饱和状态.在砂柱上表面处（由于变形小而在边界节点处）施加10 kPa的压力.假定两侧和底部不排水，仅允许水从顶面排出.数值计算中，将砂柱离散成10 个等大小的四边形单元，尺寸为0.1 m×0.1 m.使用各向同性的线弹性材料对砂土颗粒力学行为进行模拟，材料参数选择见表1，时间步长为1.0×10-7s，共计算1.0×107步.

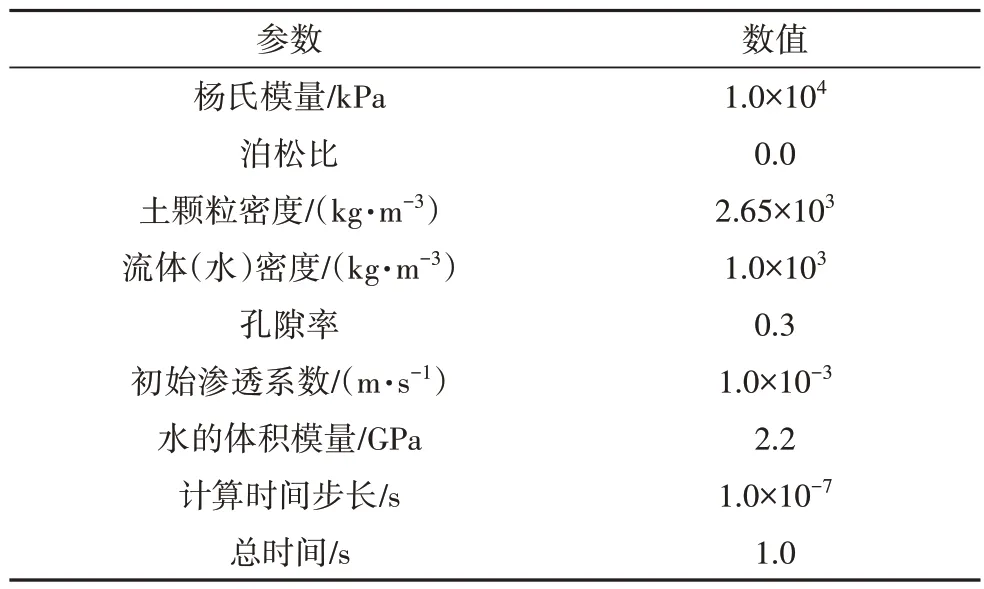
表1 一维固结试验材料特性参数Tab.1 Characteristic parameters of one-dimensional consolidation test materials

图2（b）给出了耦合物质点法（CMPM）的计算结果，并与Terzaghi 理论解进行了对比.对于各种时间因子Tv绘制图的等时线，如图2所示，其中

图2 一维固结试验Fig.2 One-dimensional consolidation experiment

式中：hv是土层的厚度；cw是固结系数，可由下式得出

由于应用了低阶线性单元，孔隙水压力在每一个单元内是恒定的，而每个单元使用了上下两排共4个积分点，因此孔隙水压力呈阶梯状分布特征，但总体而言，孔隙水压力均匀分布在太沙基理论解的两边，因此，物质点方法在解决饱和土体的流固耦合问题上是适用的.

2.2 非饱和土的入渗试验

为了验证考虑非饱和状态下的耦合物质点法（CMPM）的适宜性，本节采用并分析了Liakopoulos［19］一维非饱和砂土的入渗试验.试验装置如图3 所示，高1 m，宽0.1 m，试样采用了Del Monte 砂，材料特性参数参见表2.

图3 Liakopoulos的测试试验Fig.3 Test of Liakopoulos

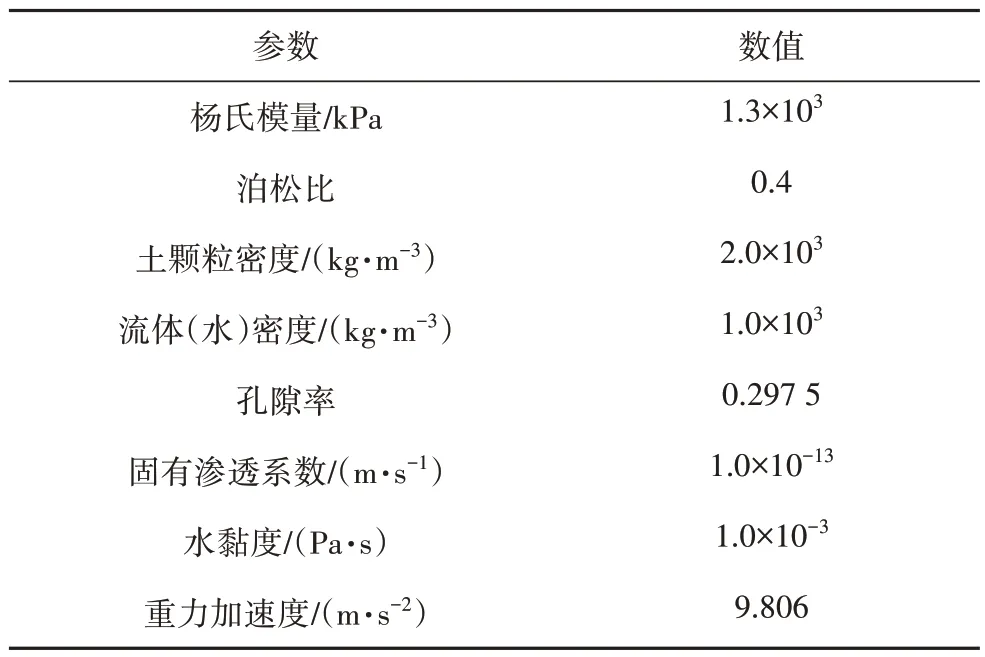
表2 材料特性参数Tab.2 Material characteristic parameter

试验具体分为两个部分，试验准备阶段和试验本身.试验准备阶段，在柱样容器内均匀布满砂子，然后从砂柱顶部不断注水，直至整个试样处于完整饱和的状态；试验开始后，停止注水，两个侧壁不可透水，而水能够从底部自由排出，这样，砂柱上半部分逐渐呈现非饱和状态，沿砂柱高度均匀布置吸力计，用于测量砂柱内部吸力分布.为计算简便，假定气体压力等于大气压力.

对于土水特征曲线的选择，Lewis 等［20］认为当饱和度Sw>0.91时，其可采取以下格式：

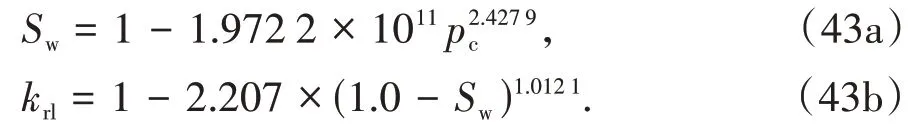
数值计算中，同样将砂柱离散成10 个大小一样、尺寸为0.1 m×0.1 m 的四节点四边形单元，时间步长为5.0 × 10-6s，共计时长120 min.试验过程中，记录了砂样在不同时刻的饱和度、垂直位移、毛细压力随高度的变化，并与Liakopoulos 试验进行了对比，结果如图4所示.

图4 CMPM计算结果与Liakopoulos试验结果比较Fig.4 Comparison of CMPM calculation results with Liakopoulos test results

整体而言，计算结果与试验结果吻合较好，说明了该方法在非饱和土中的适用性.同时，如图4 所示，随着水从砂柱样中逐渐渗出，砂柱顶部逐渐形成非饱和状态，形成毛细水吸力，饱和度变化逐渐减慢，相应地，水流出速度也逐渐降低.

2.3 降雨滑坡算例

最后，为探究耦合物质点法（CMPM）在滑坡模拟中的适宜性，本节探讨了边坡在两种不同降雨条件下的失稳破坏过程.

边坡的几何尺寸如图5 所示，高度为10 m，坡度为45°，土体特性参数如表3 所示.数值模型的背景网格尺寸为0.5 m × 0.5 m，每个单元网格基于高斯点位置插入4 个物质点，边坡结构本身表征使用了3 720 个物质点.初始孔压设置为-50 kPa.降雨边界条件通过孔压边界条件施加，即所有的降雨量都渗入边坡内部，不形成表面径流.边坡内部土体假设为理想弹塑性材料，破坏准则服从摩尔-库伦强度准则.

表3 边坡土体参数Tabe.3 Soil properties for the slope analysis

图5 边坡几何参数Fig.5 Initial geometry of the idealized slope

2.3.1 第一类降雨（持续降雨）直至产生深层破坏

图6（a）～（f）和图7（a）～（f）分别展示了不同时刻下以孔隙水压力和塑性剪切应变不变量为指标的边坡破坏过程.由图6 可看到，降雨入渗将导致边坡表面形成湿润区，孔隙水压力为0，湿润区以下的土体未受到影响，孔隙水压力为初始值-50 kPa.随着入渗时间的增加，湿润区深度逐渐增加，5 s 和10 s 的入渗深度分别为0.83 m 和1.36 m，最终在边坡表层土体重度的作用下，约在12 s 时边坡发生了较大位移，约在15 s 时发生显著变形的失稳破坏，此时入渗深度为1.86 m.随着进一步入渗的发生，边坡肩部后缘的土体也发生了坍塌破坏，如图6（f）所示.由图7可看到，降雨入渗过程中边坡产生了两条滑移面，一条位于边坡表层，一条位于边坡内部约3 m 的位置.边坡发生破坏时，土体沿着深层滑面形成了整体滑动趋势，而后表层滑移面发生加速滑动，塑性应变不变量显著增加，如图7（c）（d）所示；直至25 s时，滑体在新位置上达到新的平衡，共产生滑动距离约为12.8 m，如图7（e）～（f）所示.

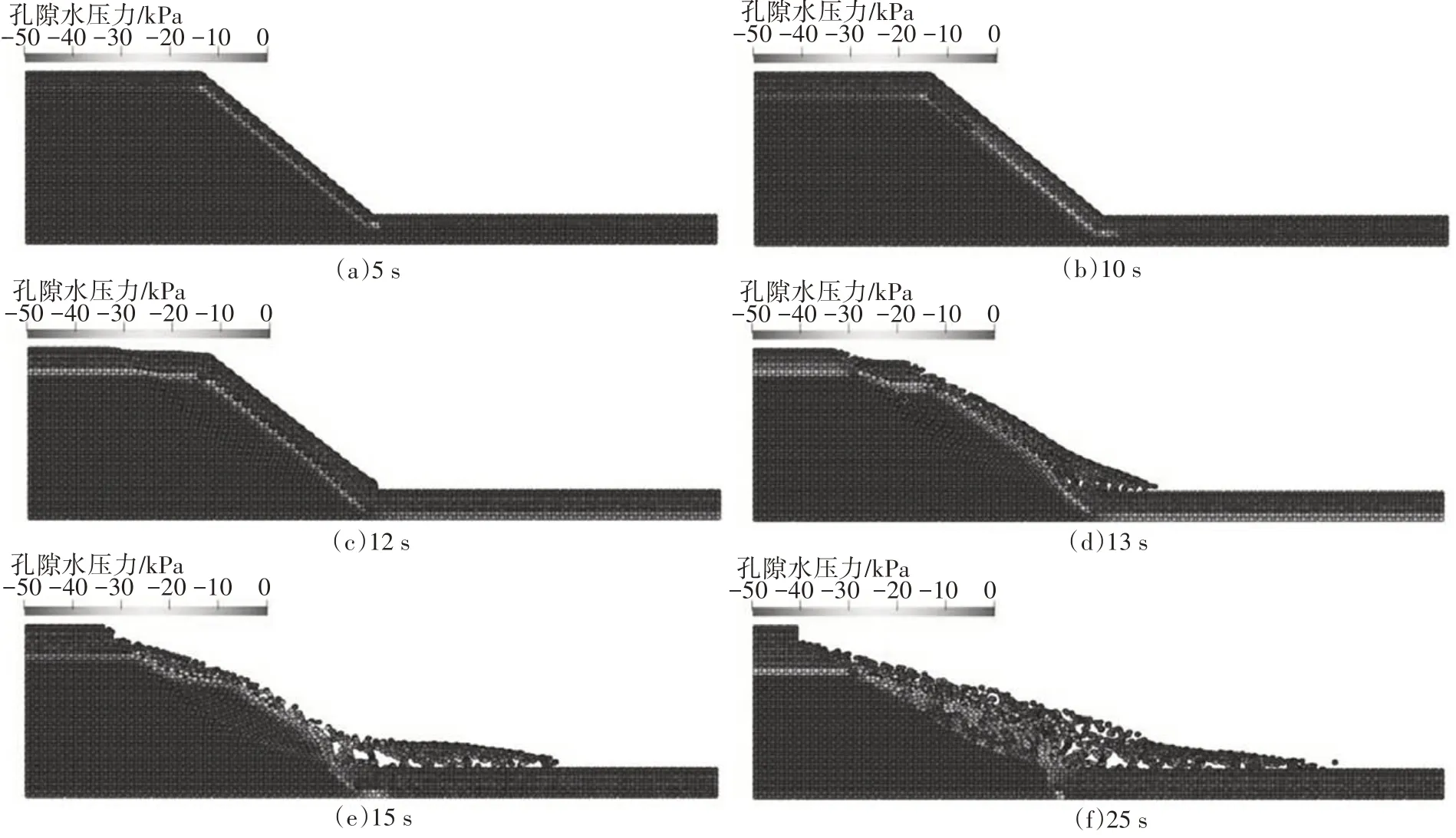
图6 第一类降雨诱发边坡失稳破坏过程中孔隙水压力分布变化图Fig.6 Pore-water pressure variations during the whole slope failure process under the first type of rainfall

图7 第一类降雨诱发边坡失稳破坏过程中塑性剪切应变不变量变化图Fig.7 Strain invariant contours variation during the slope failure process under the first type of rainfall

2.3.2 第二类降雨（短暂降雨）产生浅层剥蚀破坏

降雨时间设置为8 s，之后任其自由下渗.图8（a）～（f）和图9（a）～（f）分别展示了不同时刻下以孔隙水压力和塑性剪切应变不变量为指标的边坡破坏过程.由图8 和图9 可以看到，在短暂降雨的入渗条件下，边坡在降雨结束时首先发生了表层剥蚀破坏，剥蚀土体的滑动距离约为5.8 m；随着入渗时间的增加，湿润区逐渐增大，约在12 s 时边坡肩部发生了较大位移，约在15 s 时土体沿着深层滑移面发生滑动，边坡发生显著变形的失稳破坏.25 s 时滑坡体的滑动距离约为8.6 m.

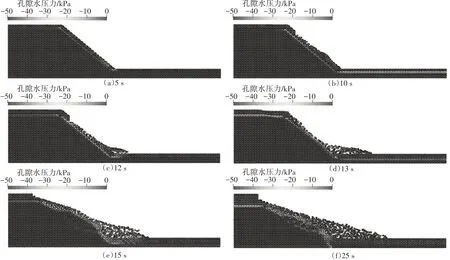
图8 第二类降雨诱发边坡失稳破坏过程中孔隙水压力分布变化图Fig.8 Pore-water pressure variations during the whole slope failure process under the second type of rainfall

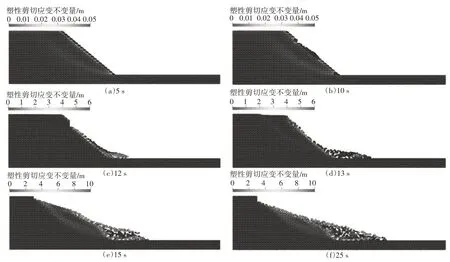
图9 第二类降雨诱发边坡失稳破坏过程中塑性剪切应变不变量变化图Fig.9 Strain invariant contours variation during the slope failure process under the second type of rainfall

综上所述，本算例中降雨诱发边坡失稳破坏主要是由于边坡表层基质吸力的降低（负孔隙水压的消散）而引起的.两类不同的降雨条件很鲜明地揭示了两种不同的破坏模式，持续降雨条件下，边坡易形成深层滑面，引起整体的滑动，浅层破坏则更多是由于深层破坏引起的二次破坏，这种破坏模式下的滑动距离主要由初始的深层破坏控制；短暂降雨条件下破坏模式则主要表现为表层的剥蚀破坏，而当初始的剥落量变得足够大时，就会进而引起渐进式的深层破坏，这种破坏模式主要依赖于边坡浅层的破坏程度.总而言之，CMPM 能够较好地模拟降雨诱发的边坡失稳破坏过程.

3 结论与展望

基于连续介质力学的质量以及动量守恒原理，考虑固-液两相非饱和材料的水力耦合作用，本文推导了基于速度场（v-w formulation）的考虑固-液两相耦合的系统控制方程.结合Terzaghi 一维固结试验、Liakopoulos 非饱和土的入渗试验，以及边坡在不同降雨条件下的破坏过程再现，验证了该计算模型在模拟非饱和土的水力耦合相互作用问题上的可靠性，对准确评价降雨滑坡的破坏过程具有重要的理论与实际指导意义.

目前的物质点流固耦合模型（CMPM）虽然通过简化引入饱和度近似模拟了降雨入渗边坡的过程，可大幅度提高程序的稳定性，但是对于耦合物质点方法的发展及应用依然有很多工作需要开展：

1）针对流固耦合问题，程序的稳定性依然是物质点方法发展的一个瓶颈，引入B-bar 形函数，使用分步法（fractional step algorithm），抑或对物质点上孔压进行光滑化等数值手段，需要进一步探究；

2）目前的工作仅讨论了孔压边界下降雨诱发边坡破坏的过程，加入流量边界，探讨不同降雨强度以及降雨模式下边坡破坏过程也是下一步需要研究的.