基于注意力机制及分层网络的危险驾驶行为预测方法

徐文翔，王俊骅，傅 挺

（同济大学交通运输工程学院，上海 201804）

危险驾驶行为表征及演化全过程一直是道路交通安全领域的研究热点［1］。准确的危险驾驶行为预测方法有助于提升现有车路协同系统警示准确度，为驾驶人提供准确的驾驶建议，从而降低交通事故发生率［2］。近年来，随着信息传感技术的日益普及，深度学习方法的不断迭代以及国内外危险驾驶行为基础研究的不断深入，危险驾驶行为预测方法的研究迎来了新的机遇［3］。然而，由于驾驶行为的随机性及交通环境的多变性，因此危险驾驶行为预测研究仍面临以下3 个方面的挑战：真实的危险驾驶行为数据采集难度高，模型训练样本少，导致模型结果缺乏一致性；危险驾驶行为预测指标选择主观性较强，未形成面向危险驾驶行为预测的规范性指标集；现有方法未完整剖析危险驾驶行为多维时序变化规律，缺乏针对性的时间窗选择及模型输入结构优化建议。

最早的危险驾驶行为数据采集主要依靠主观问卷调研方法，问询驾驶人在发生危险驾驶行为时的驾驶操作、周边环境及心理情况等，通过提取关联性指标构建危险驾驶行为预测模型［4］。传感技术的发展促进了嵌入式传感器［5］及手机GPS 技术［6］在交通领域的应用，能有效采集车辆的行驶轨迹，并捕捉出行全过程车辆数据。然而，由于缺乏驾驶人特征及道路环境类数据，因此危险驾驶行为的预测结果缺乏针对性及综合性。为了获取全时全要素驾驶行为数据，驾驶模拟技术被广泛应用于危险驾驶行为预测中。Zhao等［7］采用驾驶模拟技术构建了雾天下车路协同应用场景，并分析了不同场景下驾驶行为多维变化特征。然而，驾驶模拟技术与现实状态的偏差致使其应用受到限制。自然驾驶作为可以采集到真实的全时全要素交通环境、驾驶人状态及车辆运行数据的试验手段，越来越受到研究人员的青睐。Bagdadi等［8］基于美国100-Car自然驾驶实验数据库讨论了危险驾驶行为及各要素之间的关系，异常的纵向加速度与横向加速度是危险驾驶行为的主要因子。

在危险驾驶行为预测指标方面，主要采用单一非时序的指标对危险驾驶行为进行表征与预测。Yoshitake 等［9］将碰撞时间tTTC作为阈值构建了危险驾驶行为预测模型，Lee等［10］以tTTC＜1.0 s为阈值判别危险驾驶行为。除此之外，还将加速度相关指标作为危险驾驶行为模型构建的基础［11］。然而，危险驾驶行为的演化过程具备多指标及时序变化特征。虽然很多研究表明tTTC与危险驾驶行为高度相关，但是使用单个指标对危险驾驶行为进行预测致使预测准确率不佳。例如，在有些危险场景下，虽然具备较高的tTTC（系统提示安全），但是超速过弯、分心驾驶等危险驾驶行为仍引发了事故。为了研究多指标对危险驾驶行为的影响，Zhao等［12］采用结构方程模型，构建了不同维度指标（驾驶人状态、交通环境、驾驶操作等）与危险驾驶行为的关联性模型，结果表明不同维度指标均对驾驶行为造成了影响。因此，在预测危险驾驶行为时，驾驶操作类指标（加速度、速度等）、交通环境类指标（道路、天气等）以及驾驶人状态（性别、年龄、分心等）等均应运用到危险驾驶行为的预测中，以提升模型预测准确率。

现阶段用于时序预测的模型可大致分为3 类，即参数模型、非参数模型及半参数模型。参数模型中使用较多的是整合移动平均自回归模型（ARIMA）及其衍生模型［13-14］。该类模型仅考虑了时间维度的危险驾驶行为变化规律，在多维参数拟合方面表现不佳。非参数模型包括K-近邻算法、支持向量机、人工神经网络等［15-16］，相比参数模型，该类模型在短时预测中准确率较低［17］。为了提升非参数及参数模型的预测准确率，综合2 种模型提出了半参数模型，应用在交通领域的半参数模型包括指数平滑法、神经网络模型等［18-19］。然而，基于网络的半参数模型通常采用浅层网络或仅具有一个隐藏层，因此也无法捕获驾驶行为的时序和复杂非线性特征。近年来，随着深度学习的不断发展，越来越多的深度学习方法被应用于交通领域，其中长短期记忆（LSTM）网络及卷积神经网络（CNN）均表现出较好的适用性。Jain等［20］采用LSTM网络构建了交通流短时预测模型，该模型有效地表征了交通流预测中的时序不确定性特征。研究结果表明，LSTM 网络能较好地解决多维、时序的驾驶行为预测问题［21］。然而，现有研究多只对该模型进行了套用，在危险驾驶行为预测方面并没有形成较好的时间窗选择建议以及模型数据结构优化方法。

综上，采用自然驾驶数据，结合数据划分及视频检验方法，构建危险驾驶行为预测指标集。通过显著性分析对现有指标进行筛选和排序，设计分层数据输入模型结构，构建危险驾驶行为研究的标准指标集。构建以LSTM网络模型与注意力机制为框架的预测模型，测试不同输入结构以及时间窗下预测准确率及误差，提出用于危险驾驶行为预测的参数及结构化建议。

1 整体框架

基于注意力机制及分层网络的危险驾驶行为预测方法包括2 个模块：数据处理模块以及危险驾驶行为预测模块。如图1所示，对于数据处理模块，通过数据清洗及筛选、时间窗及变量结构调整，获得了输入模型的多维时序数据。对于危险驾驶行为预测模块，基于已有数据库，通过LSTM网络构建危险驾驶行为预测模型框架，并由注意力层优化模型参数，然后根据常规输入和分层输入结构配置全连接层，最终输出危险驾驶行为时序预测结果。

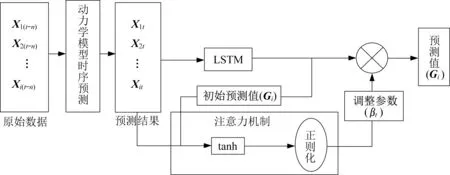
图1 模型整体结构Fig.1 System framework of the proposed model

1.1 数据处理模块

1.1.1 数据采集与清洗

自然驾驶数据通常为时序数据，采集的自然驾驶数据包括车辆轨迹数据、驾驶员属性、车辆驾驶数据、环境及周边车辆行驶数据，数据采集频率一般为10 Hz。表1为自然驾驶数据库中的数据类型及数据说明。

表1 自然驾驶数据描述Tab.1 Description of naturalistic driving data

原始自然驾驶数据存在数据缺失、数据异常、噪声以及离群值较多等问题。在数据结构调整之前，需要对已有数据进行缺失值插补、异常值识别以及数据平滑处理。由于自然驾驶数据采集频率较高，因此采用均值法处理缺失值。假设自然驾驶指标X=｛x1，x2，…，xp｝，X∈（驾驶行为数据，周边车辆数据等）存在数据缺失值xq+k，采用下式计算：

式中：xq和xj分别表示xq+k的前数据和后数据；k=(1，2，…，(j−q−1))。

由于设备精度的限制，因此数据序列中可能存在显著偏离的离群异常值。为避免异常值对后续分析造成干扰，需要对其进行识别并修复。

目前主流的异常值识别方法包括拉依达准则（3σ）、肖维勒（Chauvenet）准则、迪克逊（Dixon）准则、格拉布斯（Grubbs）准则等。格拉布斯准则是在未知总体标准偏差的情况下，对正态样本或接近正态样本异常值进行判别的一种方法。由于格拉布斯准则理论严密、概率意义明确［22］，因此选择格拉布斯准则判断异常值。判别式如下所示：

出于改善样本质量的目的，考虑到样本采集频率足够小、理论上邻近数据点间数值变化缓慢，因此采用移动平均法对整体数据进行平滑处理。最后，采用Matlab软件对数据进行清洗，获得自然驾驶数据库。

基于清洗后的自然驾驶数据，筛选危险驾驶行为状态。在危险场景指标筛选过程中，综合考虑了横向危险场景以及纵向危险场景。针对横向危险场景，采用横向加速度等指标进行危险判定；针对纵向危险场景，采用tTTC以及纵向加速度等指标进行判定。进一步选取危险场景替代指标，基于已有研究结论采用场景类判断指标以及操作类判断指标判别危险驾驶行为状态。场景类判断指标包括tTTC及超速。在判断过程中，tTTC＜1.0 s或速度＞120 km·s−1被定义为危险驾驶行为状态［23］。然而，单纯用tTTC来判定危险驾驶场景是不合理的，如危险变道等场景，tTTC判定往往无法获得较好的结果，所以在判断中引入了操作类指标。操作类指标包括横向加速度及纵向加速度指标，将不同速度分布区间中偏离原始数据区间[μ−3σ，μ+3σ]（μ为均值，σ为标准差）的数据标记为危险驾驶行为状态数据。综合场景类判断指标及操作类判断指标，2种判断情况均可能发生事故，因此在模型输出标签中，一旦符合判断标准被标记为1（危险驾驶行为），其余被标记为0（安全驾驶）。

已有研究［24］表明，冗余的指标往往导致模型拟合效果变差，为提升模型输入指标有效性，采用显著性分析对各指标与驾驶行为状态之间的关系进行判断，删除冗余指标，最终留下与驾驶行为状态显著相关的指标，作为最终的模型输入。各指标被定义为Xit=(xi(t−n)，xi(t−n+1)，…，xi(t))T，其中i表示指标，t表示时间，i的数量m由最终显著性分析结果确定。常规的模型结构（NS）仅采用单一的模型，以多个指标为输入从而拟合出预测结果，该方法仅简单地对参数进行拟合，无法达到较高的预测准确性。本研究在常规模型基础上（见图2 第2 层）提出了一种分层模型结构（FS），并通过时序模型预测得到预测结果，如图2所示。对于FS，根据操作类指标动力学特性采用神经网络算法进行时序预测，分层结构输入为各指标（tn）时刻的数据，中间输出为t时刻的预测值（第1层），然后将各指标中间输出作为预测模型的输入。基于LSTM网络与注意力机制构建预测模型，并对输入指标进行拟合（第2层），最终输出预测结果。

图2 模型输入结构Fig.2 Input framework of the proposed model

预测时间窗指驾驶人产生意图到发生操作的时间窗宽度。采用固定时间窗宽度方法，即筛选执行行为前固定时间段内驾驶行为表征指标进行模型构建［25］，或考虑驾驶人的个性特征选择不同的时间窗宽度进行模型构建［26］。相关研究表明，采用1.0～3.0 s 的时间窗宽度往往能够取得较高的预测精度［27］。因此，选择1.0～3.0 s为时间窗宽度范围，以0.5 s为间隔，将1.0、1.5、2.0、2.5、3.0 s作为模型结构的预测时间窗宽度，最终通过比对模型结果选择最合适的预测时间窗宽度。

1.1.2 LSTM网络模型

LSTM网络模型被用于危险驾驶行为时序特征提取，并通过模型训练最终对驾驶行为状态进行预测。LSTM网络结构包含1个存储单元和3个门（输入门、输出门和遗忘门）。模型内部状态主要受遗忘门和输入门的综合影响，遗忘门确定当前单元中需要保存的信息，输入门确定需要保留多少外部输入的信息，最后通过输出门将两者综合信息进行混合并输出到下一个状态。图3为LSTM网络神经元结构。相关计算如下所示［28］：

图3 LSTM神经元结构Fig.3 LSTM neuron structure

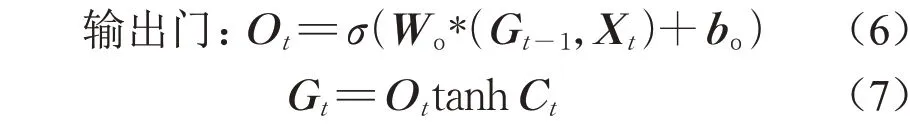
式中：Xt为当前时刻的输入；ft、it、Ot分别为当前状态下遗忘门、输入门及输出门状态；σ为激活参数；Wf、Wc、Wi、Wo为权重参数；bf、bc、bi、bo为偏置参数；Ct和Ct'为单元状态；*表示矩阵元素的乘积。3个门都以ReLU函数作为激活函数以对单元状态进行归一化。

1.1.3 注意力机制

通过探索数据内部联系，注意力机制可以自动对系统参数进行优化，并改善模型的准确率［29］。常规的危险驾驶行为预测模型未考虑变量之间的权重比例，而不同指标对危险驾驶行为状态发生的贡献率显然是不同的。因此，基于LSTM结构，加入注意力机制层，自动对危险驾驶行为指标权重进行调整。首先采用显著性分析，筛选出与危险驾驶行为显著相关的指标，然后通过注意力机制在模型计算过程中对显著性指标进行自动排序。通过两者的共同作用，提升预测模型的精度。基于注意力机制的LSTM网络结构如图4所示。

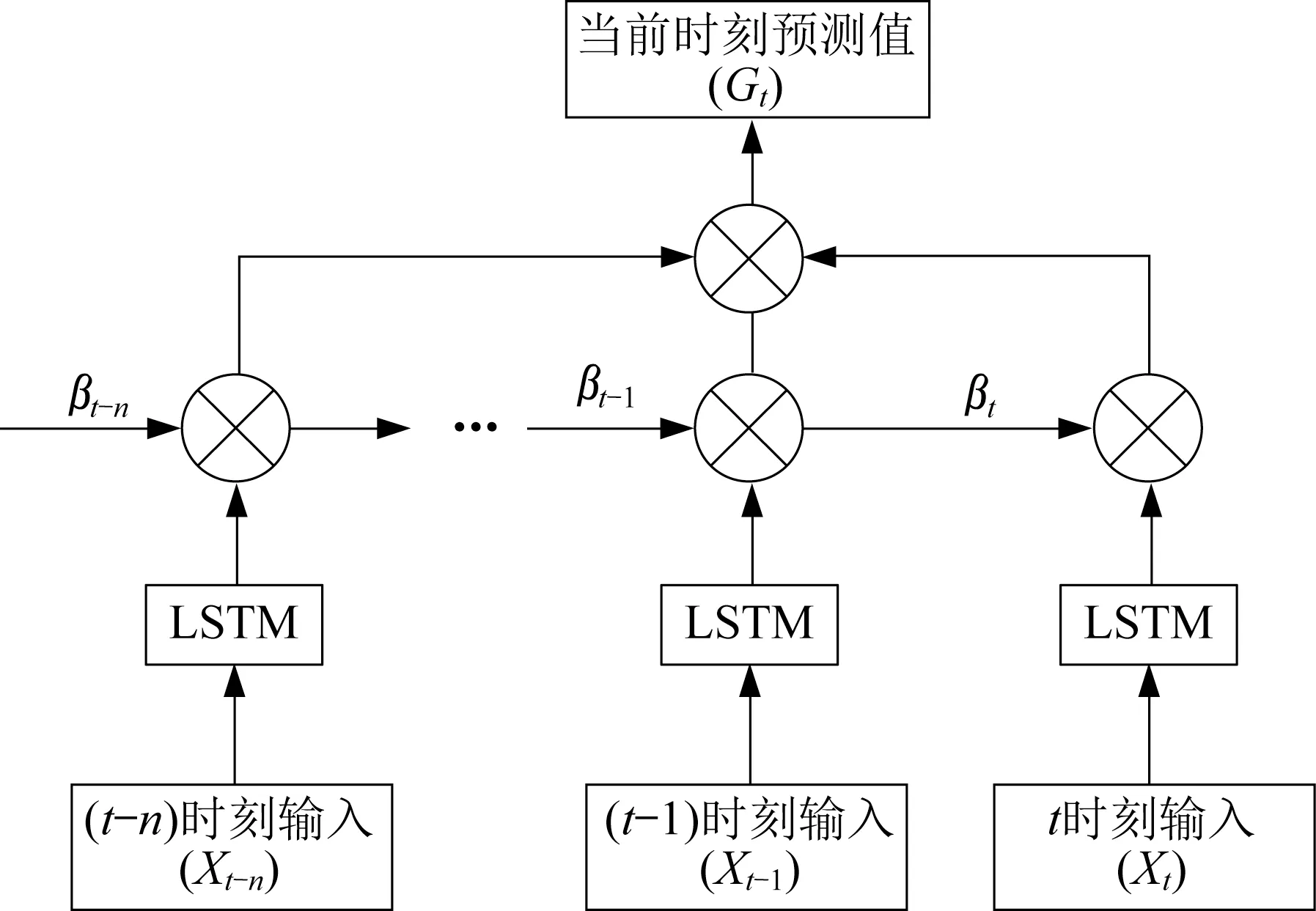
图4 基于注意力机制的LSTM网络结构Fig.4 Structure of LSTM network based on attention mechanism

对LSTM网络模型在每个时间点上的预测值权重进行计算，通过加权求和方式对预测值进行累加，并替换原预测值。权重总和计算式如下所示：

式中：vk、Wh、Wl为模型自学习参量。

注意力机制使用及其代码参见文献［30］。

采用模型准确率评价模型的好坏，并引入平均绝对误差（αMAE）作为参考。平均绝对误差定义如下所示：

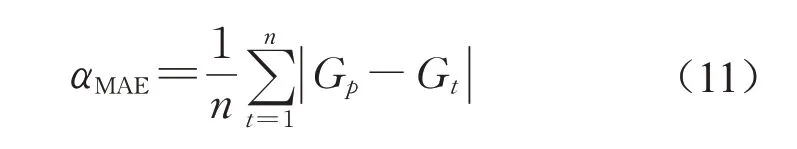
式中：Gp表示模型预测结果中危险驾驶行为状态；Gt表示实际状态。

2 模型验证及结果分析

2.1 数据采集及清洗

数据来源于上海自然驾驶实验研究（SHNDS）。实验由同济大学、通用汽车有限公司以及弗吉尼亚理工运输研究所共同开展，共招募60 名司机，通过驾驶装载了SHRP2 NextGen数据采集系统的车辆进行实验。每个车辆上都装备了可实时采集车辆加速度、速度、转向信息及通信数据的自然驾驶数据采集盒、GPS定位传感器、高精度雷达以及4台观测驾驶人与前后路况的摄像头。通过这些设备，可以采集到包括驾驶人特性、车辆运行数据、道路环境及驾驶事件等多变量的时序数据。试验数据采集频率为10 Hz，通过实验共获得了10 500例出行数据（每个驾驶人出行1 次记为1 例）。自然驾驶数据包括驾驶员的所有日常出行，必然产生与研究内容不相关的出行记录，如加油、洗车、检修、短距离出行等，由于行车时间较短，因此对应的CSV 文件或视频记录大小有限。驾驶过程必然对应较为可观的行车时间，因此将小于1 000 Kb 的CSV 文件删除，最终获得有效数据8 000 例。图5 为行驶过程中视频采集视角。

图5 摄像头视角Fig.5 Camera views

基于以上出行数据，通过缺失值插补、异常值识别与删除以及数据平滑处理，最终获得危险驾驶行为基础数据库。该数据库包含速度、加速度等操作类指标，同时也包含前后车距离等场景类指标。通过计算，获得驾驶人出行过程中的tTTC，以tTTC构建危险驾驶行为的自变量并将其作为模型的输入之一。本研究中，危险驾驶行为状态的判断可以采用场景类判断指标以及操作类判断指标。场景类判断指标包括tTTC及超速。在判断过程中，tTTC＜1.0 s 或速度超过120 km·s−1被定义为危险驾驶行为状态。操作类判断指标包括横向加速度及纵向加速度指标。采用拉依达准则（3σ），超出[μ−3σ，μ+3σ]的数据被定义为异常值。

通过危险驾驶行为判定规则，基于tTTC异常、超速及横纵向加速度数据设置标签。根据前文定义，当满足危险驾驶倾向及危险场景参数时，驾驶行为标签为“危险=1”，其他情况下标签为“安全=0”。采用Matlab 软件根据该逻辑对数据进行筛选，最终从8 000 份出行数据中采集到危险驾驶行为发生点854 个，包括该点以及该点之前3.0 s 内所有采集到的数据。为了获得驾驶人属性及外部环境数据，同时提升危险驾驶行为数据标签准确性，通过视频记录对854 个点进行验证，验证标准如表2 所示。表2的分类参考《公路交通安全设施设计规范》《中华人民共和国道路交通安全法》等，并根据实际需求进行调整。为了降低人工标记误差，仅派出2 名实验人员进行标记，并在视频标记前进行了严格培训，保证数据的一致性及有效性。经过人工筛选，最终500例危险驾驶行为数据（包括危险发生前3.0 s 数据）以及1 000例安全驾驶行为数据（随机从安全数据中采集）被用于模型的训练及验证。表2 是实验中所采集的数据以及其量纲。

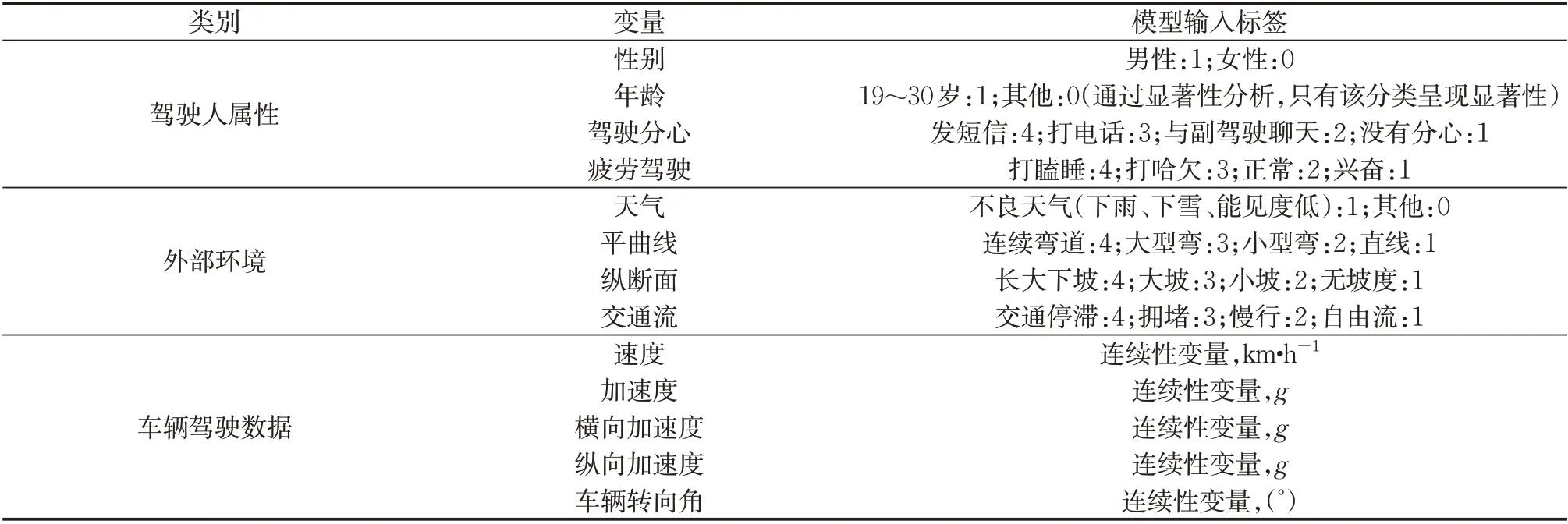
表2 变量描述Tab.2 Description of variables

为了提升模型预测准确度，降低误差，对现有指标与危险驾驶行为状态之间的显著性进行验证。通过显著性分析，将显著性指标作为模型最终输入。有8个变量被运用到危险驾驶行为模型构建中，分别是性别、疲劳驾驶、天气、平曲线、纵断面、速度、横向加速度以及tTTC。各指标显著性及指标描述性统计如表3所示。

表3 变量显著性及数值Tab.3 Significance of variables and their values

2.2 危险驾驶行为预测模型

采用TensorFlow 框架［31］构建基于注意力机制的LSTM 网络模型（Attention-LSTM）。为了确定合适的时间窗宽度，共选用了5种时间窗宽度（1.0、1.5、2.0、2.5、3.0 s）作为输入时间窗宽度，然后构建了2种模型结构。对于NS，共有8个输入变量，直接输出二分类结果（危险=1，安全=0）。对于FS，同样有8 个输入变量，其中车辆驾驶类指标（速度、横向加速度以及tTTC）作为单独输入进入第1 层，并获取时序预测的中间输出，作为下一层的输入；驾驶人属性指标以及外部环境类指标在出行过程中保持不变，直接进入下一层。以往的研究表明［32］，在动力学特征研究方面，前向反馈神经网络以及径向基神经网络具备较好的预测效果。因此，采用2 种预测方法进行对比，经过结果的比对选择准确率最高的预测方法作为第1 层预测模型。第2 层的输入为第1层模型预测结果加上5个不随出行变化的变量。第1层预测方法的准确率如表4所示，结果表明前向反馈神经网络更适用于对操作类指标的预测，精度达到87%左右，尤其在时间窗宽度为2.0 s 时，预测精度最高。因此，采用前向反馈神经网络算法作为第1层模型的预测方法。

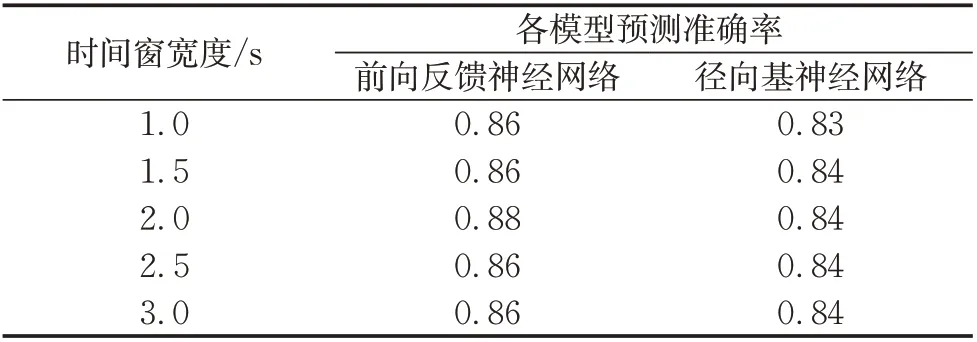
表4 不同时间窗下第1层模型预测结果Tab.4 Prediction results of the first layer models at different time intervals

第2层的输入变量仍为8个，通过变量拟合输出的二分类结果即该时刻下驾驶行为状态（危险=1，安全=0）。为了验证模型的准确性，采用7∶3的训练比进行模型测试。模型采用成本最小化函数（Adam）进行优化，将ReLU作为激活函数，为了防止过拟合，设定0.5为模型退出阈值。采用平均绝对误差（αMAE）验证模型误差。为了验证所提模型的适用性，对比注意力机制的作用，分别对NS 与FS 中的LSTM 以及Attention-LSTM网络模型的准确率及误差进行计算。模型预测结果准确率及误差如表5所示。

由表5 可知，注意力机制可以有效提升模型准确率（约3%）并降低模型误差。无论在FS中还是在NS 中，注意力机制都能有效提升模型预测准确率。进一步验证所提出分层模型结构的有效性，以Attention-LSTM 模型为例验证NS 以及FS 预测准确率。结果表明，提出的FS能较好地提升模型准确率（约5%），尤其在时间窗为2.0 s 时提升效果最明显（6%）。FS 也能有效降低误差，从侧面反映了该结构的有效性。

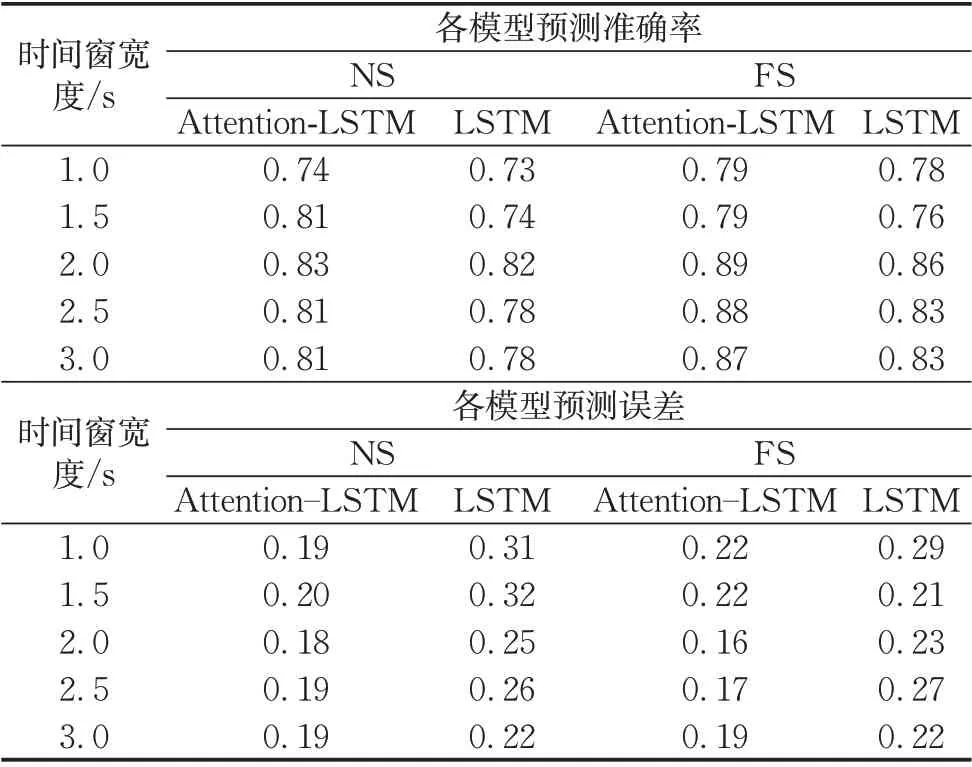
表5 不同时间窗下各模型预测结果Tab.5 Prediction results of models at different time intervals

由表5可知，最合适的时间窗宽度为2.0 s，该时间窗宽度在2 种模型结构中优势均较为明显，表现为较高的准确率以及较低的误差。在FS下，预测精度达到了最高值（89%）。原因可能是2.0 s 的时间刚好是驾驶人从做出反应到事件发生之间的时间差。因此，在危险驾驶行为研究中可以使用2.0 s作为预测时间窗宽度。

为了验证所提出的模型的有效性，将所提出的模型与现有常用的二分类模型进行对比［33］，主要包括逻辑回归模型（LR）、支持向量机模型（SVM）、随机森林模型（RF）以及卷积神经网络（CNN）。如图6所示，所提出模型的预测准确率明显高于其他模型（约10%）。对比不同模型在不同时间窗宽度下的准确率，各模型在2.0 s时的表现较好，普遍高于其他时间窗宽度。综上，Attention-LSTM模型及分层输入的方法能有效预测危险驾驶行为，以2.0 s作为时间窗宽度时，预测效果最佳（89%），并且误差最小（αMAE为0.16）。

图6 模型预测结果Fig.6 Prediction results of models

3 结语

提出了一种基于注意力机制及分层网络的危险驾驶行为预测方法。通过优化模型结构对驾驶全时全要素信息进行保存，同时引入注意力机制，然后通过网络自学习权重将LSTM网络所有时刻的输出重新排序，并对输入信息权重进行优化。对比不同宽度时间窗下模型预测准确率及误差，给出了危险驾驶行为预测的参考时间窗宽度。结果表明，所提出模型能有效提升危险驾驶行为时序预测准确率并降低误差，在时间窗宽度为2.0 s时模型表现最好。

作者贡献声明：

徐文翔：数据分析，基础模型构建，初稿撰写。

王俊骅：提出论点，构建论文框架，初稿修改，模型优化。

傅 挺：论文修改，模型优化，数据分析。