估计大规模MIMO-OFDM稀疏随机信道的卡尔曼滤波
张 静,张梦雨,王 栋
(上海师范大学 信息与机电工程学院,上海 200234)
0 引言
大规模多输入多输出(MIMO)即多天线是第五代移动通信提升频谱效率、能量效率和传输可靠性的主要技术之一。正交频分复用(OFDM)具有高传输速率和抗频率选择性衰落的优点,因而被广泛地与MIMO相结合。通常,大规模MIMO-OFDM系统的无线多径信道具有空时结构化稀疏性,采用压缩感知(CS)理论中的稀疏信号恢复算法来估计信道参数已成为主要方法[1]。
当信道参数为确定定常信号且呈现稀疏性时,在OFDM和MIMO-OFDM系统中可设计合理的导频图案以达到最优或近最优的估计性能[2]。在单观测向量(SMV)条件下,通过基扩展模型来表征复信道衰落特性后,用贪婪类重构算法包括正交匹配追踪(OMP)及改进算法来恢复信道参数是稀疏度已知时的常见算法[3],文献[4]提出了在稀疏度先验知识未知时的自适应匹配追踪算法(SAMP)。当信道参数为随机时变时,可采用稀疏卡尔曼滤波(KF)在多测量向量(MMV)条件下获取信道参数。在文献[5]中,把OFDM系统中慢衰落的稀疏信道冲激响应和脉冲噪声共同视为未知的稀疏向量,对以一阶自回归模型表示的慢时变信道进行跟踪,提出了一种联合信道和噪声的估计算法;在文献[6]中,把MIMO-OFDM稀疏时变信道估计中的加权L1范数最小化问题转化为非线性等式约束卡尔曼滤波问题,构造了一个伪观测方程并线性化;在文献[7]中,提出了一种用于毫米波MIMO-OFDM系统的基于叠加导频设计场景中的稀疏KF来获取信道参数;在文献[8]中,针对毫米波多天线滤波器组多载波(MIMO-FBMC)系统的双选稀疏信道估计问题,设计出基于稀疏贝叶斯学习的在线KF算法对信道跟踪。
由于待估计参数的真实范数未知,所示不能直接构成观测量进行修正,极大地影响了KF的收敛精度和速度,因而在MMV条件下的稀疏KF常与其他算法相结合。稀疏信号为平稳随机信号时,文献[9]为恢复合成孔径雷达稀疏图像,用KF算法取代OMP算法中的最小二乘估计来得到支撑集的索引,形成了KF嵌套在贪婪算法内的算法结构;文献[10]通过构造递减的L1范数伪测量,结合稀疏KF与阈值迭代算法来恢复视频稀疏信号。当稀疏信号的字典矩阵或支撑集为快时变时,文献[11]提出基于贝叶斯学习的动态滤波方法;文献[12]采用2级方法来恢复时变支撑集,第1级利用快速的稀疏贝叶斯匹配追踪获得支撑集的索引,第2级使用改进的最小二乘估计和QR分解来缩小支撑集;文献[13]结合稀疏贝叶斯学习,用双卡尔曼滤波器从含噪声的传感器信号中对序列状态和参数辨识;文献[14]把稀疏KF与平滑技术相结合;文献[15]提出了一种基于稀疏约束的增广KF,将空间稀疏先验信息通过伪测量方程引入滤波模型;文献[16]量化了在估计稀疏信号和支持集中存在的测量损耗,给出了在给定信息丢失率时预测估计误差协方差的上界。
在MMV条件下,当多个联合稀疏向量具有公共的支撑集且为平稳向量时,可利用二阶统计量来分析。文献[17]为恢复超高次谐波稀疏信号,利用测量向量的自相关矩阵将MMV模型分解为多个SMV模型,再用OMP算法恢复出谐波信号,此时估计结果为各单测量时恢复信号的平均值;文献[18]将原问题转化为选择非负的超参数的诱导高斯先验,求解在观测空间中的一组近似正则化凸优化问题,提出了一种指数梯度更新方法以降低计算量、存储量和收敛所需的迭代次数。文献[19]讨论了在稀疏向量的非零行固定时,对支撑集渐近成功恢复所需的测量个数和测量噪声方差的充要条件。
本文用稀疏KF方法来求解大规模MIMO- OFDM信道参数的恢复问题,将无线多径信道建模为平稳随机信道,提出基于L1范数最小化优化模型和滤波算法,设计出二步KF算法重构信号;再将KF与贪婪算法中基于回溯的硬阈值迭代算法结合,进一步改善重构精度和收敛速度。通过仿真对比验证了方法的性能。
1 系统模型
设一个大规模MIMO-OFDM系统具有Nt根发射天线、Nr根接收天线和K个OFDM子载波。记发射端天线的索引为m、载波的索引为k、子信道的有限冲激响应拍数索引为l;把第m根发射天线的发射信号用xm=[xm(0),xm(1),…,xm(K-1)]∈K表示,则在第k个子载波上的接收信号可表示为:
(1)
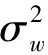
频域信道Hm(k)可进一步表示为:
(2)
在某一根接收天线处的接收信号矢量为:
(3)
式中,diag(xm)表示由发送符号矢量构成的对角矩阵; (F)K×K表示K点傅里叶变换矩阵;hm为信道的有限冲激响应。
设导频图案为梳状且每个OFDM符号中有KP个导频,用p∈{1,2,…,K}表示导频所在的位置并用xm(p)表示导频符号,则可得到对应在Kp个导频处的接收信号矢量,它由式(3)中的y抽取Kp行得到。因而在时刻n的测量方程为:
y(n)=Ah(n)+W(n),
(4)
式中,A=[X1(F)Kp×KX2(F)Kp×K…XNt(F)Kp×K]为测量矩阵,A∈Kp×Nt K;h(n)=[h1(n),h2(n),…,hNt]Τ为NtK×1维信道矢量;W(n)为测量噪声,设其协方差矩阵为R。
将该传输系统的复信道衰落参数建模为:
h(n+1)=h(n)+ω(n),
(5)
式中,ω(n)表示过程噪声向量,设各分量统计独立、方差相等并将其协方差记为Qω(n)。
同时,设基站处的发射天线排布紧密,故多根发射天线和一根接收天线之间的有限冲激响应有非常相似的路径延迟,不同收发天线对的有限冲激响应可视为共享一个时域稀疏模式,即子信道的有限冲激响应视为K拍,但仅在前L拍是多径衰落,而后K-L拍为零,同时,设多根发射天线有公共的散射体,不同发射天线和某一根接收天线之间的空域稀疏模式也相同。因此,分别有:
h(n)=[h1(n),0,h2(n),0,…,hNt(n),0]T,
(6)
supp{h1(n)}=supp{h2(n)}=…=supp{hNt(n)}。
(7)
2 L1范数最小化卡尔曼滤波
2.1 优化目标
设e(n)=Y(n)-Ah(n),将大规模MIMO-OFDM稀疏信道的重构问题表示为一个基跟踪去噪优化问题的求解:
(8)
式中,拉格朗日乘子λ为正则化参数,用于控制稀疏解的稀疏度,可以平衡误差方差和L1范数这个双重目标函数。
根据稀疏信号恢复的原理,在SMV条件下,若h(n)的稀疏度为S,当A满足约束等距性条件,则可在式(4)欠定且满足KP≥2S时准确重构出h(n)。常见的求解算法有Bregman迭代算法。
在可获得N个测量向量即MMV条件下,假定hn=[h(n-N+1),h(n-N+2),…,h(n)]具有固定的非零行且稀疏度S保持不变,在序列递推过程中,欲从N个观测向量Yn=[y(n-N+1),y(n-N+2),…,y(n)]中恢复出h(n),则优化问题可表示为:
(9)
2.2 KF-L1算法
基于KF对优化式(9)进行求解。首先,由于被估计稀疏信道参数的真实范数值无法观测,利用当前估计值的L1范数,建立伪观测模型:
(10)
式中,γ(n)是为使L1范数值逐渐递减而引入的一个随机下降因子,0<γ(n)<1,为保证算法收敛,γ(n)随着n的增加逐渐增大,当n→∞时趋近1;v(n)是第n次递推L1范数时的观测噪声,设其协方差矩阵为Rv且为恒定,即Rv(n)=Rv。
接着,由于L1范数这个非线性函数不存在微分,故利用其次微分对式(10)线性化。对复信道衰落向量,其L1范数的次微分可以表示为:
(11)
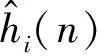
由此可求得雅可比矩阵为:
(12)
因此,可基于以式(5)为状态方程和以式(4)和式(10)为测量方程的滤波模型,设计完全KF-L1算法。但是,由于正则化参数λ往往未知,且L1范数的次微分一般较小,对新息的修正量很小,同时用2类测量来递推估计时,由伪测量所产生的新息和由测量方程所产生的新息对参数的修正互相耦合,会较难分辨由伪测量所产生的小量修正,导致收敛时间长且信道重构误差较大。
2.3 二步KF-L1算法(TKF)
完全KF-L1算法增广了伪测量后对L1范数和L2范数同时修正,容易使数值稳定性较差。事实上,式(9)这个正则化优化问题可以分割成2个优化问题:L1范数的最小化和L2范数的最小化,从而使优化问题的求解更为简单。
因此,本文提出将优化过程分为2步:最小化估计均方误差和最小化L1范数,采用2个依次进行的KF来获取复衰落。在用式(5)和式(10)构成KF的状态空间模型和测量模型后,做如下递推。
用式(5)对h进行一步预测,可得:
h(n+1|n)=h(n),
(13)
并计算估计误差协方差的一步预测为:
P(n+1|n)=P(n)+Qw(n)。
(14)
再用式(10)对测量值进行一步预测,有:
z(n+1|n)=γ(n+1)‖h(n+1|n)‖1。
(15)
预测后,更新状态向量为:
h1(n+1)=h(n+1|n)+
β1(n)[z(n+1)-‖h(n+1|n)‖1],
(16)
式中,β1(n) 为增益矩阵,
β1(n)=P(n)CH(n)[C(n)P(n)CH(n)+Rv]-1。
(17)
接着,用当前的估计值作为一步预测值,再用式(4)进行第二步KF,修正测量误差,即修正增益矩阵:
β2(n)=P(n)AH(n)[A(n)P(n)AH(n)+R]-1。
(18)
修正当前估计值为:
h(n+1)=h1(n+1)+β2(n)[Y(n+1)-Ah1(n+1)]。
(19)
修正估计误差协方差为:
P(n+1)=P(n+1|n)-β2(n)AP(n+1|n)。
(20)
该算法的流程如算法1所示。

算法1:TKF滤波算法输入:A,h(0),P(0),Y(n),Q(n),Rv(n),R(n),γ(0),ε输出: h(n)若h(n+1)1-h(n)1>ε循环计算: ① 由式(13)和式(14)计算预测状态和协方差② 由式(15)计算预测输出③ 由式(11)计算雅可比矩阵 ④ 由式(17)计算增益矩阵⑤ 由式(16)更新状态⑥ 由式(18)再次计算增益矩阵⑦ 由式(19)修正状态⑧ 由式(20)更新估计误差方差
2.4 贪婪卡尔曼滤波(GKF)
TKF算法利用L1范数的次微分来修正稀疏信道,但并未提取稀疏信号的支撑集,导致收敛过程较慢。为缩短递推收敛过程,本文引入了基于回溯的迭代硬阈值(BIHT)算法来贪婪地估计支撑集。BIHT算法在回溯的解码框架中,选择最可能张成编码空间的多个支撑向量张成空间。如果估计向量到这个空间的距离较大,则根据它们的可靠值,递增地消除和增加新的基向量,直到确定出一个充分靠近的候选支撑集合。
本文在TKF算法的基础上,在用常规KF获得了当前估计值后,利用BIHT法来获得支撑集的索引。先按估计向量中各分量的绝对值降序排列,获得前S个最大绝对值的索引,即有:
supp{h(n)}=Ω1。
(21)
接着,用该支撑集计算估计向量为:
(22)
式中,HS{·}表示保留前S个绝对值最大的非零元素,其他元素置为零;μn为步长下降因子。
通过调节μn来提高算法收敛速度,在每步递推中,令:
(23)
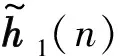
supp{h(n)}=Ω1∪Ω2=Ω3,
(24)
然后用新的支撑集更新估计:
h(n)=AΩ3†Y(n),
(25)
再用这个新的估计值作为当前值序列递推。
在MMV条件下,引入BIHT算法的目的是更新支撑集,寻找到前S个绝对值最大的非零元素,即寻找到h中元素的L2范数值最大的S行。应用BIHT算法时大多需要已知稀疏度,但在此信道估计问题中难以获得稀疏度先验信息,而且基跟踪去噪优化算法也不需要已知稀疏度。尽管贪婪算法在稀疏度未知时会挑选出错误的原子造成支撑集的误判,但是这种误判所带来的估计偏差受测量噪声的影响。在MMV条件下随着伪测量的递推修正,在较高信噪比(SNR)时仍然可以得到较好的稀疏解。因此,考虑到通过导频设计所构成的测量矩阵的行数应大于或等于预设稀疏度的2倍,即KP≥2S,故在GKF算法中用KP/2来替代BIHT算法中的真实稀疏度以得到实用算法。
该算法的流程如算法2所示。

算法2:GKF滤波算法输入:A,h(0),P(0),Y(n),Q(n),Rv(n),R(n),γ(0),ε输出: h(n)若h(n)1-h(n-1)1>ε① 用式(4)和式(5),按常规KF算法得到h(n)② 挑选h(n)支撑集的索引集,得到Ω1③ 由式(23)计算步长μn④ 由式(22)计算h~1(n)⑤ 挑选h~1(n)支撑集的索引集,得到Ω2⑥ 由式(24)合并支撑集⑦ 由式(25)更新估计h(n)
3 仿真结果与分析


(26)
图1表示在用SMV条件下的Bregman迭代算法和MMV条件下的KF-L1算法、TKF算法和GKF算法恢复稀疏信道时,NMSE随SNR变化的性能曲线。从图中可以看出,用SMV的Bregman迭代算法在低SNR时NMSE性能较差,在SNR达到12 dB之后,其NMSE性能介于TKF和GKF算法之间;在较低SNR时,TKF具有最小的NMSE性能,KF-L1算法和TKF算法的NMSE性能较为接近,在较高SNR时,GKF算法的NMSE性能最优。

图1 算法的归一化均方误差与信噪比的关系Fig.1 Normalized mean square error versus signal-to-noise ratio of the algorithms
从图1中还可以看出,TKF算法在SNR=9 dB时的NMSE与GKF相当,这说明此时用贪婪算法中的最小二乘法所获得的估计精度与KF的估计精度相当,最小二乘法与KF都是最优估计,但随后TKF算法的估计精度低于GKF算法,这表明TKF算法在未获取估计参数的支撑集时,会受到非支撑集的观测列向量对估计的影响;另一方面,在SNR大于12 dB后,TKF算法的NMSE大于SMV-Bregman算法,这说明当SNR充分大时使用单测量向量即可得到较高的恢复精度,而用伪测量的TKF算法的NMSE精度改善趋于平缓,但Bregman是定常稀疏参数的恢复方法,它没有利用随机稀疏参数的动态特性。
进一步分析该现象可以得知,信道参数的最稀疏解是最小化L0范数的解。由于L0范数的非凸性,通常用L1范数来简化求解过程。在含有噪声的观测方程下,对基跟踪去噪优化模型求解并且在SNR较低时,对观测值迭代逼近的SMV-Bregman算法无法有效地消除噪声对参数估计的影响,故性能有限;而MMV相较于SMV提供了更多的费希尔信息,使用MMV条件下的KF可滤除噪声并平滑估计值,是从有噪声的观测数据中估计动态随机参数的最佳方法,故性能有所提升,但递推估计需要的计算量较大。
图2表示在SNR=9 dB时,TKF算法和GKF算法重构信道的幅值及位置与真实值及位置之间的关系。可以看出,2种算法在此时可以有效地确定非零元素的位置,也能较好地重构稀疏信号,但2种算法均在非支撑集位置处呈现小量误差。这一方面是由于没有准确的稀疏度信息而采用了基跟踪去噪模型的递推迭代算法,另一方面是测量噪声和信道模型系统噪声的影响。通过仿真还可得知,当SNR增加到12 dB以上后这种小量误差随之减小,2种算法都能更为准确地获取支撑集,估计参数的归一化均方误差趋于很小量。再有,TKF用2个KF迭代来滤除噪声影响,而GKF算法引入贪婪算法后对L1范数失去了滤波性能,受测量噪声的影响较大,故在SNR较低时TKF算法的NMSE性能更优。
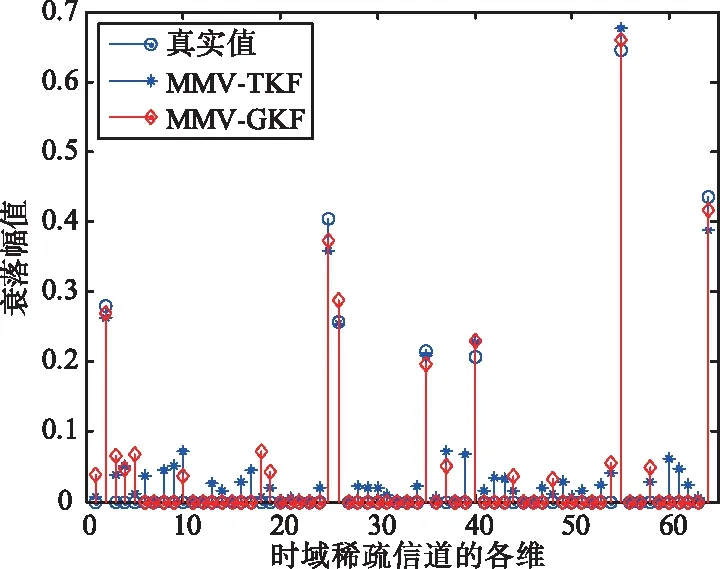
图2 恢复信道的幅度与真实值对比Fig.2 Comparison of amplitude of recovery channel with real value
图3为 在SNR=9 dB时2种算法的复衰落估计和L1范数的均方误差收敛曲线。从图中可以观察得出,TKF算法和GKF算法的收敛速度远快于完全KF-L1算法,完全KF-L1算法和TKF算法的复衰落估计均方误差的收敛速度快于L1范数均方误差收敛速度,这表明L1范数的可观性较弱修正较慢,TKF算法在递推约1 800次后才达到收敛,而GKF算法的收敛速度很快。

图3 算法的均方误差收敛曲线Fig.3 Mean square error convergence curve of the algorithms
通过这些仿真结果可知,TKF算法虽然在较低SNR时有效地提高了估计精度,但其收敛速度仍然较慢,随着SNR的提高,TKF算法的NMSE性能低于GKF算法;GKF算法可显著提高收敛速度,但在低SNR时性能还略差。因此,在设计恢复算法时应在估计性能和收敛速度上折中考虑。
4 结束语
针对大规模MIMO-OFDM结构化稀疏随机信道的获取问题,在MMV条件下建立了优化模型并设计了2种算法。在建立了L1范数伪测量模型并进行线性化后,为克服用完全KF恢复时易陷入局部极小值的困难,提出了二步滤波算法TKF,并利用回溯硬阈值迭代来估计支撑集以改善收敛过程。仿真结果表明,2个算法均能较高精度地重构稀疏信道,贪婪KF算法具有性能稳定、收敛快的优点。研究稀疏KF在快时变稀疏信道中的重构能力将是下一步的重点。

