面向边缘协作的动态服务配置与迁移机制研究

杜 楚 ，黄泽锋，李小翠

(1.中国电子科技集团公司第五十四研究所，河北 石家庄 050081；2.河北省智能化信息感知与处理重点实验室，河北 石家庄 050081；3.中国地质大学(北京)信息工程学院,北京 100083)

0 引言

近年来，物联网设备的普及催生了许多新兴物联网应用，如智能家居、智慧城市、实时制造和患者监测等。这些物联网应用通常表现出严格的服务质量(QoS)要求，如低延迟和低能耗等，对物联网设备有限的资源与计算能力带来了重大挑战[1-3]。边缘计算成为缓解新兴物联网应用低延迟要求和设备资源受限之间冲突的首选平台[4-6]。边缘计算支持在靠近终端用户的边缘服务器上配置服务，用户可以将复杂的计算任务卸载到附近的边缘服务器，实现快速响应和实时计算任务处理[1]。因此，在边缘计算下，服务实时配置到距离终端用户最近的边缘服务器上的同时，满足用户请求约束的QoS是一个关键挑战。此外，当终端用户请求的服务未配置在请求的边缘服务器上时，为保证QoS，考虑将用户任务通过当前请求的边缘服务器迁移到临近的边缘服务器运行，或将临近边缘服务器上配置的服务动态迁移到当前边缘服务器。因此，利用边缘服务器之间协作，动态服务配置与迁移机制研究对于边缘计算下减少用户请求服务访问延迟和降低设备能耗开销至关重要。

边缘计算下的任务动态配置和迁移受到了广泛关注。许多研究者致力于设计有效算法来提升QoS和降低成本。任务分配决策在服务配置中起着关键作用，Chen等[7]通过对各参数的联合优化，设计了一种能量最优动态计算卸载方案。文献[8]为了最小化任务的卸载时间，设计了一种基于延迟依赖的优先级感知任务卸载策略，根据任务的截止时间为每个任务分配优先级。文献[9-12]集中于部分卸载策略或协同优化卸载决策和资源配置。大多数相关研究只关注任务卸载以解决延迟和能耗限制，而忽略了用户的服务请求在实际情况下是高度动态的。边缘节点可能没有配置任务所需的服务，这会限制任务卸载策略。考虑服务请求的多样性与边缘节点有限的服务数量之间的冲突，文献[13]提出将服务从云迁移到网络边缘。但是，云服务器和边缘节点之间通信的时间和能源成本很高。因此，频繁地从云到边缘节点的服务迁移会导致延迟和能耗增加。文献[14]提出在边缘节点之间迁移服务，使可用服务更接近用户设备，减少服务迁移的额外成本。文献[15]解决了何时何地迁移服务以在QoS和迁移成本之间实现最佳权衡的挑战。文献[16-18]侧重在动态网络环境中实现低延迟服务迁移和无缝计算。任务卸载和服务迁移问题可以建模为马尔可夫决策过程(MDP)，利用强化学习算法获得MDP的最优策略。

边缘节点之间的协作(例如任务卸载和迁移)降低了设备的能源消耗，提高了QoS约束。以上研究大多数分别考虑这2种协作策略，并没有将服务配置和迁移有效地结合起来。因此，本文提出了一种高效的计算任务卸载策略，将任务卸载与服务迁移策略动态结合，以最小化任务处理成本。本文的主要贡献包括以下3点：

① 基于现实的任务请求模式与任务协作处理方式，分析了若干种任务请求模式的特征，归纳出多种请求情况，并制定了相应的迁移和卸载策略。

② 提出一种新的边缘协作策略，在考虑传统的纵向迁移和横向卸载协同方式的同时引入服务横向迁移的方式，并行执行任务卸载和服务迁移过程，减小了数据传输延迟，达到网络整体能量消耗及响应延迟的最小化。

③ 通过对多种请求场景的分析，将选择任务执行地点问题建模成多维马尔可夫决策过程，利用深度强化学习算法并合理设置该算法的状态空间、动作空间和奖惩函数等属性，实现该问题快速决策。

为了评估该策略的可行性及高效性，本文对所构建的边缘计算网络下的任务协同处理问题进行了模拟仿真实验。实验结果表明，本文提出的策略可以有效地降低网络整体延迟以及能量损耗。

1 相关工作

1.1 边缘计算下的任务卸载

任务服务配置决策在边缘计算中起着关键作用。通过对各参数的联合优化，文献[7]提出了一种能量最优动态计算卸载方案。考虑各个边缘节点的能量效率和优先级，提出了公平任务卸载方案[9]。文献[10]引入了一种新的动态边缘计算模型，并设计了一种在线原对偶算法来卸载到达的任务。为了提高卸载算法的泛化能力，文献[11]提出了一种基于元强化学习的任务卸载方法。考虑边缘节点资源受限，文献[12]提出了一种资源感知自适应任务卸载框架，灵活选择最优卸载策略。

但是，这些算法没有考虑到用户请求的服务可能没有在执行节点上配置。这项工作引入了一种动态计算卸载策略，将具有丰富计算资源的中间节点作为任务的执行节点。如果执行节点没有配置相应的服务，服务迁移过程并行进行。本文采用深度强化学习算法快速决策最优中间节点。

1.2 边缘计算下服务迁移

边缘节点有限的服务和用户时延敏感约束给边缘计算下开展服务配置与迁移带来了更多的挑战。为了实现低延迟和无缝计算，边缘节点间的服务迁移备受关注。文献[16]提出了一种基于用户活动热点的服务迁移策略，根据用户活动热点图，提前在边缘节点上部署服务。文献[17]开发了一种基于松弛和舍入的最优迭代求解方法来最小化迁移成本。文献[14]将服务迁移问题表述为非线性 0-1规划问题，并设计了基于粒子群的服务迁移方案。然而，由于传统启发式算法时间复杂度高，难以实现算法的快速收敛。强化学习正在成为优化服务迁移策略的一种有前途的方法，文献[18-20]提出了服务迁移的决策过程建模为一维马尔可夫决策，以服务迁移延迟为目标函数，提出利用强化学习优化服务迁移决策，实现算法快速收敛，有效地减少迁移过程中的额外延迟和能量消耗。

综上所述，这些方法在特定的场景下节能效果十分显著，但是并不适用于本文的场景。因此，本文提出了一种高效的计算任务卸载策略，采用深度强化学习实现快速决策，并将服务迁移与任务动态卸载相结合。

2 网络和性能模型

本节介绍了系统模型，包括网络模型、能耗模型和时延模型3个部分。

2.1 网络模型

网络基本要素主要包括边缘节点的描述、服务和任务描述以及时间片的划分，具体的定义如下：

① 该研究场景中，网络包括N个边缘节点，将这些边缘节点表示为集合F={F1，F2，…，Fi，…，FN}。对于这些边缘节点，通过以下几个属性来描述：边缘节点的唯一标识Fi.id、边缘节点的地理位置Fi.Loc=(Lx,Ly)、边缘节点当前托管的服务列表Fi.HostLst、边缘节点当前正在处理的任务列表Fi.PT以及处理器频率Fi.Fre。其中，i∈[1,N],Lx为边缘节点地理位置的经度，Ly为边缘节点地理位置的纬度。不失一般性的前提下，本文考虑所有边缘节点的资源相同，资源包括CPU处理能力、带宽、内存和存储。

② 本文网络中包括了M种类型的服务，将这些服务类型标记为集合S={S1，S2，…，Si，…，SM}，并通过以下几个属性来描述：服务的唯一标识Si.id，服务的大小Si.Bytes和服务重配置所需的时间Si.RCT，其中，i∈[1,N]。服务重配置所需的时间与服务本身所占用的大小无直接关系。

③ 将时间段T均匀地划分为相等的时间片，将其标记为T={T1，T2，…，Ti，…，Tt}。

④ 每个时间片下，假定用户会发出K个任务请求，将其标记为C={C1，C2，…，Ci，…，CK}。对于这些任务请求，通过以下几个属性来描述：任务请求的地理位置Ci.Loc=(Lx,Ly)，任务请求的类型Ci.Sj，任务请求的数据量大小Ci.Bytes以及任务处理所需的CPU时钟周期Ci.Cir。其中，i∈[1,N]，j∈[1,M]，Lx为发出请求的用户的经度，Ly为发出请求的用户的纬度。

2.2 能量模型

对于每个任务请求，其所需的总能耗为：

Etotal=Ecomp+Etti+Eftji，

(1)

式中，Ecomp为该任务的计算处理能耗；Etti为任务卸载到边缘节点Fi的能耗；Eftji为服务从边缘节点Fj迁移到边缘节点Fi的能耗,i∈[1,N]，j∈[1,M]。

通信能耗模型的参数及其相关参数如表1所示。Etti和Eftji都是通信时将数据包从i点发送到j点产生的能耗，根据FORM模型，对于kbyte从节点发送到距离为d的节点的过程,，可以表示为：

Ecmm,ij(k,d)=ETx(k,d)+ERx(k)，

(2)

ETx(k,d)=Eelec×k+εamp×k×dn，

(3)

ERx(k)=Eelec×k，

(4)

式中，ETx(k,d)为将数据大小为k的数据转发到距离为d的节点所消耗的能量；ERx(k)为接收kbyte数据所消耗的能量。传播衰减指数n的值受环境影响较大。若设备之间传输数据时没有建筑物遮挡，可将n的值设置为2，否则根据具体的环境可设置为3，4或5。Eelec和εamp分别表示单位能耗常数和发射放大器单位能耗常数。

表1 一阶无线电模型参数

2.3 时延模型

对于每个任务请求，其所需的总延迟为：

Dtotal=Dcomp+max(Dtti,ArgMin{Dfttji}+Dr)+Dw,

(5)

式中，Dcomp为该任务的计算处理时间；Dtti为任务转发卸载到边缘节点Fi的时间；Dftji为服务从边缘结点Fj迁移到边缘节点Fi的时间；Dr为服务的重配置时间；Dw为任务请求处理的等待时间，i∈[1,N]，j∈[1,M]。Dttti和Dfttji都是通信时将数据包从i点发送到j点产生的时延，本文将无线传输时的延迟定义为：

delay=knetlgdij+bnet,

(6)

式中，dij为i点与j点的距离；knet和bnet定义如下：

knet=44.9-6.55lg(hb)，

(7)

bnet=46.3+33.9lg(f)-13.82lg(hb)-ahm+cm，

(8)

式中，f为信号频率，单位MHz；hb为节点的天线高度；cm在一般情况下设置为3 dB;ahm定义如下：

ahm=3.20(lg(11.75hr))2-4.97，

(9)

式中，hr为用户设备的高度。单个任务的计算时延Dcomp定义如下：

(10)

式中，C.Cir为任务处理所需的CPU时钟周期；F.Fre为边缘节点的处理器频率。

2.4 目标函数定义

整个网络的能耗和延迟成本定义为所有任务的能量消耗之和以及所有任务的时延之和的加权和，目标函数定义如下：

(11)

式中，Ditotal为所有任务请求完成所需的时延总和；Eitotal为所有任务请求完成所需的能量总和；ω1和ω2分别是控制权重的参数。

3 基于DQN服务配置与迁移

在强化学习算法中，对于每个时间片Tτ，产生系统状态Sτ，并计算上一时刻的奖励Rτ-1。根据预先定义的策略选择动作Aτ。执行该操作后，系统将在下一个时间片中转换到新状态Sτ+1。同样，再次计算奖励Rτ并根据状态Sτ+1选择新动作Aτ+1。

3.1 服务配置状态空间

系统状态基于延迟、能耗、边缘节点托管的服务类型、边缘节点的运行状态以及当前时间片的所有请求信息。系统总延迟和总能耗如下：

(12)

即，Xi,j(t)为t时刻，请求i在边缘节点Fj上执行的总延迟Dtotal。

(13)

即，Yi,j(t)为t时刻，请求i在边缘节点Fj上执行的总能耗Etotal。

综上所述，系统在t时刻的状态可以表示为：

St={X(t),Y(t),F.HostLst,F.rt,C.Loc,Ci.S}∈S，

式中，S为系统的状态空间。

3.2 服务迁移动作空间

动作空间被定义为等待处理的任务请求的候选执行地点集，即所有的边缘节点集合以及云节点，系统Tτ时刻的动作可以表示为一维向量：

At= {aF1,aF2,…,aFN,ac}∈A，

式中，A为所有可执行的动作，每一个元素值代表了该请求是否在此处执行，其值为1时代表在此处执行，其值为0时代表不在此处执行；Fi为边缘节点；c为云节点。

3.3 服务配置与迁移奖惩函数

本文的目标是最小化延迟和能耗，因此，系统Tτ时刻的奖励定义为：

Rt=M1-(Dtotal(t)+Etotal(t))，

(14)

式中，M1为常数值；Dtotal(t)，Etotal(t)分别表示时刻t产生的任务请求的处理延迟以及能量损耗。

3.4 服务配置与迁移算法设计

本文采用了DNN和 Q-Learning相结合的深度Q-Learning算法。在深度Q-Learning算法中，使用Q-Network存储Q矩阵，该网络由权重为θ的DNN组成，可以有效存储Q值信息。算法1描述了深度Q-Learning算法。对于每次迭代，首先获取初始状态S0，对每个时间片τ，根据预先定义的策略选择动作Aτ，并获取下一个状态Sτ+1。通过式(14)计算奖励，更新Q-Network并最终输出动作Aτ。

算法 1:基于服务迁移和边缘协作的DQN算法输入:θ:Q-Network的权重D:经验重放池输出:Aτ:动作算法流程:1:for episode = 1,M do2: 获取初始状态S03: 初始化D3: for τ= 1,k do4: 调用算法2选择动作Aτ 5: 获取状态Sτ+16: 通过式(14)计算Rτ7: 调用算法3,根据Sτ,Sτ+1,Aτ,Rτ,D更新Q-Network8: 输出动作Aτ9: end for10:end for

3.4.1 动作选择

动作选择基于epsilon-greedy策略，该算法主要包括2个部分：探索者及开发者。预设一个ε阈值，每次选择时产生一个随机值Φ，当Φ大于ε，则由开发者进行动作选择；否则通过探索者进行动作选择。具体动作选择过程如算法2所示。

算法 2:动作选择输入: Sτ:当前状态 BD:最佳动作表输出: Aτ:动作算法流程: 1:产生随机值Φ 2:ifΦ>εthen 3: 通过开发查找最佳动作表BD,得到Aτ 4:else 5: 获取可用计算资源列表L 6: 从资源列表中随机选取边缘节点Fi,得到对应的Aτ 7:end if

3.4.2 Q-Network更新

在Q-Learning算法中，每个Q(Sτ-1，Aτ-1)都可以用如下规则更新：

Q(Sτ-1,Aτ-1)←(1-α)Q(Sτ-1,Aτ-1)+

α[Rτ-1+γ×maxAτQ(Sτ,Aτ)，

(15)

式中，α为学习率；γ为折扣率。在深度Q-Learning算法中，Q值信息一般都被抽象存储在DNN中，由于系统状态会在每个时刻Tτ不断变化，因此DNN需要自适应地进行更新。目标网络提供稳定的Q(Sτ，Aτ;θ’)，其y(τ)定义如下：

yτ=E{(1-α)Q(Sτ-1,Aτ-1;θ′)+

α(Rτ-1+γmaxQ(Sτ,Aτ;θ′))}，

(16)

式中，θ′为目标网络的权重，会间歇地重置回θ。

算法3描述了Q-Network更新过程。在该算法中，对于每个时刻，都将经验四元组(Sτ，Aτ，Rτ，Sτ+1)存储在经验重放池D中，然后在D中抽取一组四元组用于更新网络。对于每个四元组(Sτ-1(j)，Aτ-1(j)，Rτ-1(j)，Sτ(j))，计算Q(Sτ(j)，Aτ(j);θ’) 和y(τ)。

3.5 服务配置与迁移算法复杂度分析

在算法1中，算法时间复杂度主要包括动作选择算法和Q-Network更新算法。其中，对于行2及行5的状态观察和收集，其时间复杂度与需要收集的状态的个数有关，即边缘节点的个数N，对于K个任务请求，需要预计每个任务请求在各个边缘节点上运行的延迟和能耗，因此该步骤的时间复杂度为O(K×N)。对于行4，其时间复杂度取决于动作选择算法，开发过程只需要查找最佳动作表，因此时间复杂度为O(1)，探索过程需要在可用资源列表中随机选择动作，在3.3节已经分析过该步骤的时间复杂度为O(N)。对于行6，其时间复杂度取决于奖励函数的计算，具体为O(N+M+K)。对于行7，其时间复杂度取决于Q-Network的更新，其时间复杂度取决于经验重放池D的大小，大小取决于状态空间S的大小和动作空间的大小A，状态空间大小为边缘节点和云节点的个数之和N+1，动作空间大小一般情况下为边缘节点的个数N，故可得该算法时间复杂度为O(N2)。

4 结果评估

实验程序的运行环境为：64位Windows10操作系统、16 GB内存、处理器为Intel(R) Core(TM) i7-3770 CPU @ 3.40 GHz以及显卡NVIDIA GeForce GTX 1070 Ti，通过Python程序实现。为保证实验的科学性，所有实验均在同一环境下进行。

4.1 实验设置

本实验中的参数设置如表2所示。

表2 实验参数设置

网络区域为500 m×500 m，该区域中均匀分布了50个边缘节点。由于边缘节点的资源限制，每个边缘节点上最多可配置H=2种服务。通常一个物联网部署之后，会根据节点的部署情况，选择一个合适的通信范围，为了保障该网络的连通性，本文将边缘节点的通信半径设为150 m。边缘节点的CPU频率F.Fre=2 GHz。任务处理所需的CPU时钟周期C.Cir∈[50,200]单位时间。信号频率f=2.5 MHz，天线高度hb=35 m，用户设备高度hr=1 m。无线信号传输的带宽wi=500 MHz，无线传输的能量消耗常数Eelec=50 nJ/bit，传输放大器的能耗常数εamp=0.1 nJ/(bit·m2)。CPU单循环的计算能耗为6×10-9Wh。成本函数的时延权重ω1=0.8，能耗权重ω2=0.2。

对于DQN中的网络参数设置，学习率α=0.1，折扣率γ=0.9。对于DNN的结构，本文使用4层全连接层的神经网络，该网络的设置基于实验结果。本文对网络的深度设置开展了大量实验，结果表明，4层的网络在本文的问题场景以及数据下有较好的表现。本文将状态St和动作At对表示为元组，并转换成12 127×1的向量，将其作为DNN的输入。在DNN的第1层和第2层之间添加了线性整流激活函数。DNN的输出则是St和At元组的Q值对。需要注意的是，在该网络中，所有的边缘节点有着相同的DNN结构和权重。

4.2 实验结果

本实验通过观察系统长期的平均延迟以及能耗来探索不同的系统参数设置对该策略的影响，这些系统参数包括任务请求的稀疏度以及服务类型的个数。

4.2.1 任务请求稀疏度

当任务请求的稀疏度越高，平均每个时刻产生的任务请求会越多，则系统的平均响应延迟以及能耗会越高。为了研究任务请求的稀疏度对平均延迟和能耗的影响，本文实验将任务请求的稀疏度prob设置为0.2，0.4,0.8。不同任务请求稀疏度设置下系统平均延迟如图1所示。

图1 不同任务请求稀疏度设置下系统平均延迟Fig.1 Average system delay under different task request sparsity settings

系统的平均响应延迟与每个时刻的任务请求数量成正比，即与任务请求的稀疏度成正比，但从图中可以观察发现，稀疏度prob=0.4时，相比于稀疏度prob=0.2时的系统平均延迟没有增加至一倍，其原因是prob=0.2时，在密集部署边缘节点的网络中，该网络的计算负载是不饱和的，因此接收到任务请求时，边缘节点往往可以立即处理该任务请求。而稀疏度prob=0.4时，该网络的计算负载接近饱和，此时任务请求开始出现不能在最合适的边缘节点上立即处理的情况，边缘间协同处理情况开始变得频繁。prob=0.8时，该网络的计算负载过饱和，因此平均延迟相比于稀疏度prob=0.4时翻倍。

不同任务请求稀疏度设置下系统平均能耗如图2所示。直觉上，系统的平均能耗与每个时刻的任务请求数量成正比，即与任务请求的稀疏度成正比，因为无论系统是否处于饱和的状态，任务请求是否由于计算资源不足导致延迟增加都与能量损耗没有直接关系。由图2可以看出，当系统计算负载接近饱和时，开始出现较频繁的服务迁移和任务卸载，这些任务协同处理方式必然会导致传输能耗增加，因此，系统的平均能耗与任务请求的稀疏度成线性增加的关系。

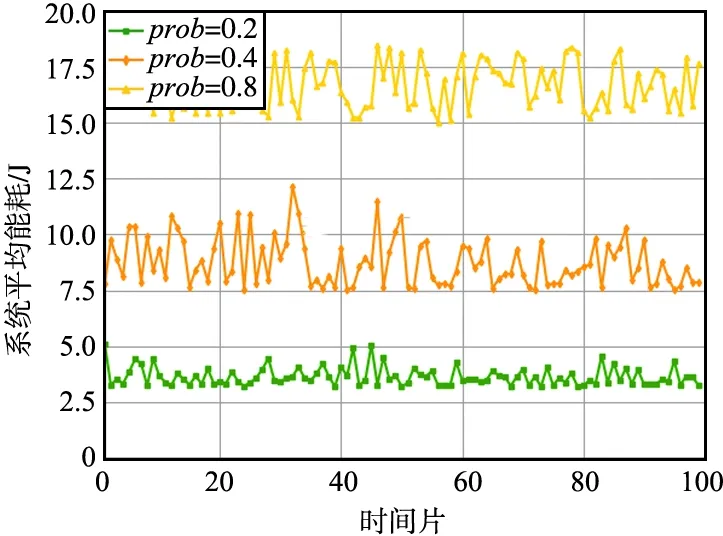
图2 不同任务请求稀疏度设置下系统平均能耗Fig.2 Average system energy consumption under different task request sparsity settings

4.2.2 服务类型的个数

不同服务类型数量设置下系统平均延迟如图3所示。

图3 不同服务类型数量设置下系统平均延迟Fig.3 Average system delay under different service types and quantity settings

服务类型数量snum=50时，系统的平均延迟与图3中prob=0.4的系统平均延迟基本一致。当snum=20时，所有服务类型都可以在边缘网络中找到多个配置了该服务类型的边缘节点，因此服务迁移和任务卸载的地点有了更多候选，也更容易找到与数据产生地点邻近的任务处理地点。因此，在边缘网络的计算负载还没有完全饱和时，随着服务类型snum值减小，系统的平均响应延迟也越小。值得一提的是，当snum=100时，系统平均延迟的波动率显著增加，分析这一现象可能的原因是边缘层配置的服务出现了“脱靶”的情况，即任务请求的类型可能在边缘层级上没有找到配置了相应服务的边缘节点，配置了相应服务的边缘节点计算资源不足或者其物理距离不够邻近也可能造成该问题。在这种情况下，边缘节点为保障任务能有效处理，必须将任务卸载至云端或者将云端中的服务类型迁移至边缘层，这种远距离的迁移或者卸载都会导致任务的响应急剧增加，从而出现了图中系统平均延迟波动率增加的情况。因此，当服务类型数量远多于边缘层所能配置的服务数量时，为尽量减少脱靶的情况，如何对边缘层的服务进行合理的预配置，以及在迁移时如何保证边缘层服务的丰富度是亟需研究的问题。

不同服务类型数量设置下系统平均能耗如图4所示。

图4 不同服务类型数量设置下系统平均能耗Fig.4 Average system energy consumption under different service types and quantity settings

由图4可以看出，相比于系统平均延迟，服务类型数量snum=100时，边缘网络的系统平均能耗波动率更大。如图4所示，波动率增大的原因是发生了脱靶情况，这种情况导致边缘节点不得不进行远距离的迁移和卸载，但受益于第3节提出的围绕计算资源的策略，边缘节点在任务处理时是将可用的计算资源作为迁移和卸载的中继点，并通过服务迁移和任务卸载使其存在时间、空间上重叠，因此该策略在发生远距离边缘间协作时，可以有效降低任务处理的延迟，但是边缘节点的数据量传输的距离没有太多变化，因此相比于系统平均延迟，系统的平均能耗在脱靶时代价更大。

5 结束语

针对服务请求高度多样且动态变化的情况，如何对计算、存储和带宽等资源限制的边缘节点实时服务配置与迁移，使网络的总体能耗以及请求延迟尽量最小化，本文提出了一种基于服务迁移和边缘协作的服务动态重配置策略，降低任务请求处理过程中的时延以及能耗。根据所提策略设置深度强化学习算法的状态空间、动作空间和奖励函数，并利用深度强化学习进行任务处理地点的决策，解决传统启发式算法由于复杂度过高无法在时延敏感的场景中使用的问题。为了验证本文提出策略的可行性和高效性，探索了2种不同的网络参数因子对该策略的影响，并且对比了2种传统的任务协作处理方式，实验结果表明，本文所提策略可有效降低系统任务处理延迟，并且一定程度上可以减小系统能耗。