频谱非对称包络调制的圆对称艾里光束的传播特性研究*

宁啸坤 耿滔

(上海市现代光学系统重点实验室,上海理工大学,上海 200093)

为了增强圆对称艾里光束的自聚焦能力,本文使用了非对称双曲正割函数对光束的频谱进行了包络调制研究,详细探讨了频谱中高、低频分量对自聚焦特性的影响.结果表明单纯增加频谱的高频分量,并不会使自聚焦能力持续增强,低频分量对光束的自聚焦特性同样起着不可或缺的作用.由于非对称包络可以灵活的调节高、低频分量的比重,因此调制效果要优于高通滤波和对称包络调制.当调制参数选取适当时,光束焦点峰值大幅增加,达到了调制前的3.4 倍,同时焦斑尺寸减小了23.6%.最后,本文对理论分析结果进行了实验验证,实验结果与理论结果相吻合,证明了频谱的非对称包络调制是一种高效且易于实现的调制方法.

1 引言

自2007 年首次实验产生有限能量的艾里光束以来[1,2],其无衍射、自加速等特性受到了研究者的极大关注,是光学领域的研究热点之一[3−5].随后,圆对称艾里光束(circular Airy beam,CAB)[6]、艾里阵列光束[7]、分数艾里光束[8]等新型艾里光束也被逐渐提出.其中,将一维艾里光束做径向对称处理获得的CAB 是一种特殊的自聚焦光束,其特点是在自由空间中传播时,在焦点前能保持着极低的光强分布,而到达焦点处时,其光强会突然提升至之前的数十倍甚至数百倍,因此又被称为突然自聚焦光束(abruptly autofocusing beam,AAB)[6].与普通聚焦光束相比,CAB 在焦点位置前能保持极低的光强分布,因此被用于激光手术治疗和光动力治疗等领域时,不会对其传播路径上的健康细胞造成损伤,从而能实现精准定点治疗的效果[9].CAB在焦点位置的光强发生突变,因此能产生一个极大的光学梯度力,在光学微操纵[10,11]等领域内有着极强的先天优势.近年来,Papazoglou 等[12,13]发现CAB 在非线性介质中可以产生与基波保持相同相位分布的高阶谐波,这种“相位记忆”特性在非线性光学领域有着广阔的应用前景,已被应用于“光子弹”和太赫兹辐射的产生[14,15].

对于上述应用而言,CAB 的突然自聚焦特性至关重要,因此如何尽量提升光束的自聚焦性能成为研究者关注的核心问题之一.Li 等通过在初始平面遮挡CAB 的主光环,提升了CAB 的自聚焦效率[16].随后,Jiang 等[17]提出了傅里叶空间频谱的高通滤波方法,发现比遮挡主光环能获得更好的结果.Zhong 等[18]在波前引入了角向调制来控制光束的自聚焦性能,但由于预期光束的结构远比CAB 复杂,实验中较难产生[19].Li 等[20]提出了使用部分相干性来调控CAB 的自聚焦性能.最近,我们提出了频谱振幅的包络线调制方法[21],在频谱空间引入了高斯对称包络调制,使得光束的焦点光强增强为原CAB 的2.9 倍.

频谱包络调制方法的优点在于能够灵活控制频谱的宽度和不同频段在频谱中的能量占比,且易于实验实现.为了便于计算,在前期的工作中我们仅使用了简单的对称高斯函数作为包络函数[21],然而对称包络调制无法有效的调节高、低频分量在频谱中的占比,因此不能充分发挥频谱包络调制方法的优点,而且无法很好的分析高、低频组分在自聚焦过程中的作用.

基于上述原因,为了分析频谱中高、低频组分对自聚焦特性的影响,并进一步提升光束的自聚焦性能,本文使用了非对称双曲正割函数对CAB 频谱进行了包络调制研究.通过改变调制参数,详细分析了频谱中高、低频组分对光束自聚焦特性的影响,并寻找到了合适的调制参数,使得调制效果明显优于对称包络调制.最后,本文利用傅里叶变换法实验产生了调制光束,验证了理论分析结果,发现实验结果与理论结果相吻合.

2 理论与分析

在柱坐标系中,CAB 初始面的光场分布可以表示为[6]:

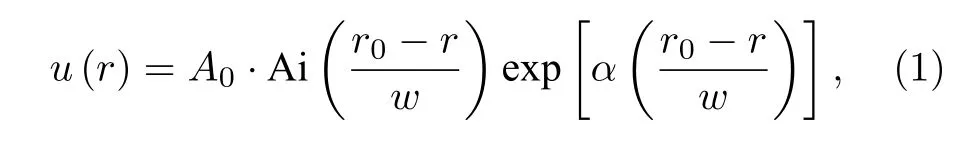
式中,A0为振幅常数,A i(·) 表示艾里函数,r0代表主光环的半径,w为比例因子,α为指数衰减因子(0<α<1).目前,CAB 的频谱还没有严格的解析表达式[22],通常使用傅里叶变换计算获得[23]:

式中,C表示振幅常数,以保持调制前后频谱能量守恒,EV(k) 是 频谱函数绝对值 |F(k)| 的包络函数.由于 |F(k)| 缺乏严格的解析表达式,EV(k) 只能通过数值计算获得,可以通过数值求解微分方程dF(k)/dk=0 寻找其极值点对应的kn值,下标n表示第n个极值点,然后利用线性插值的方法就可以得到EV(k) 近似值,如图1(b)所示.

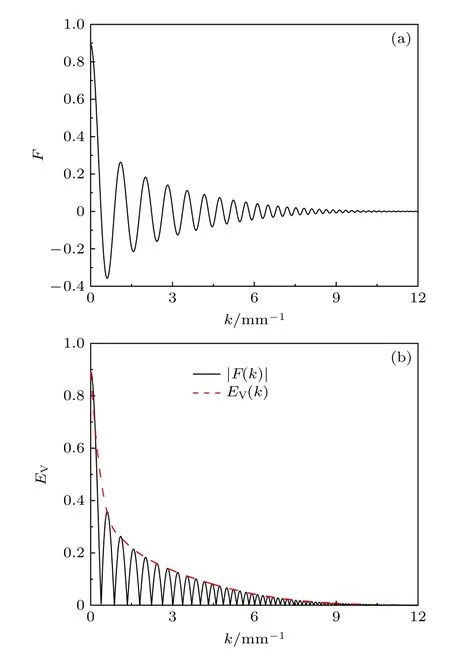
图1 参数 r0=1 mm ,w = 0.1 mm,α =0.1 时 (a) CAB的频谱 F (k) ;(b) CAB 频谱的绝对值 |F (k)| 及其包络曲线EV(k)Fig.1.Calculation results of (a) F (k) ,(b) |F (k)| and EV(k) with r0=1 mm ,w = 0.1 mm and α =0.1.

(3)式中,A HS(k) 是非对称双曲正割函数,其公式为

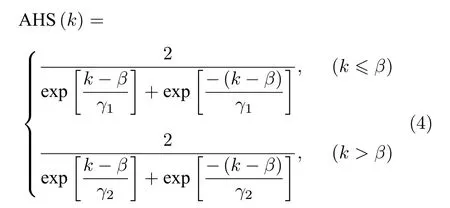
式中,β决定了包络函数的中心频率位置,如图2(a)所示,随着β增大,中心频段向高频方向移动.图2(b)给出了经图2(a)的频谱调制后,相应的初始面光强分布,从图中可以看到,随着β增大,初始面的峰值光强位置向外移动,由于要保持总光强不变,因此光强峰值随之降低.(4)式中,γ1,γ2可分别用于控制低频、高频组分的频谱的宽度,如图2(c)和图2(e)所示,图2(d)和图2(f)则分别给出了调制γ1,γ2后相对应的初始面光强分布.从图2(d)中可以看到,随着γ1的增大,由于低频组分的增加,初始面光环数量沿着中心方向增多;与此相对,随着γ2的增大,由于高频组分的增加,初始面光环数量背离中心方向增多,如图2(f)所示.由于初始面总光强保持不变,光强峰值随着光环数量的增多而降低.

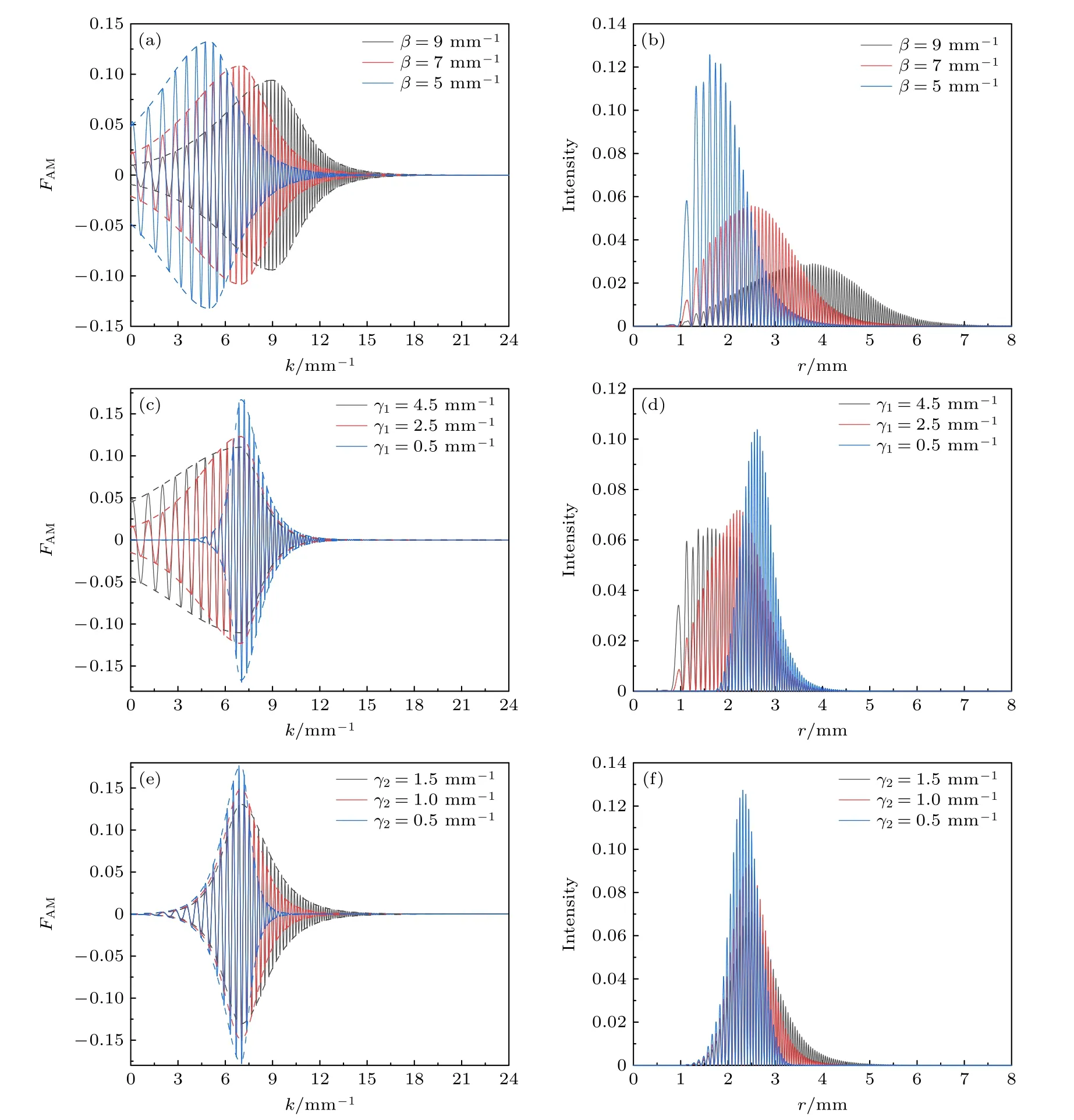
图2 不同调制参数的AMCAB 的频谱分布以及相对应的初始面光强分布 (a) γ1=3 mm−1,γ2=1.5 mm−1 保持不变,β 不同时的频谱分布及相对应的(b)初始面光强分布;(c) β =7 mm−1、γ2=1 mm−1 保持不变,γ1 不同时的频谱分布及相对应的(d)初始面光强分布;(e) β =7 mm−1,γ1=1 mm−1 保持不变,γ2 不同时的频谱分布及相对应的(f)初始面光强分布Fig.2.Spectrum distributions and corresponding intensity distributions of AMCAB at the initial plane with different parameters.(a) Spectrum distributions and (b) corresponding intensity distributions with different β when γ1=3 mm−1,γ2=1.5 mm−1 ;(c) spectrum distributions and (d) corresponding intensity distributions with different γ1 when β =7 mm−1,γ2=1 mm−1 ;(e) Spectrum distributions and (f) corresponding intensity distributions with different γ2 when β =7 mm−1,γ1=1 mm−1.

为了便于书写,本文将非对称包络调制后的CAB简称为AMCAB (asymmetric modulated circular Airy beam,AMCAB),将对称高斯函数包络调制后的CAB 简称为GCAB (Gaussian-modulated circular Airy beam).

图3(a)给出了CAB 的侧面光强分布,从图中可以看出,其能量占主导地位的内光环遵循抛物线轨迹向着中心光轴传播,但传播过程中有较多的能量弥散在空间中,此时CAB 的焦距约为656 mm.图3(b)给出了β=8.3 mm−1,γ1=5.5 mm−1,γ2=0.1 mm−1的AMCAB 的侧面光强分布,从图中可以看到AMCAB 与CAB 有类似的突然自聚焦特性,但聚焦前能量分散于各光环中,相比于CAB,传播过程中弥散在空间的能量明显减少,其焦距约为655 mm,与CAB 的焦距几乎相同.

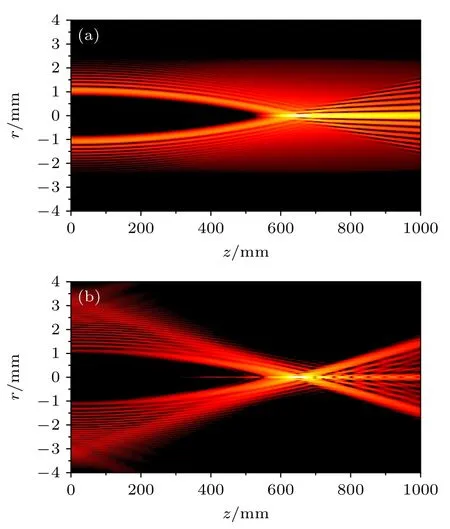
图3 CAB 和AMCAB 的侧面光强分布 (a) CAB;(b) β=8.3 mm−1 ,γ1=5.5 mm−1 ,γ2=0.1 mm−1 的AMCABFig.3.Propagation dynamics of CAB and AMCAB: (a)CAB;(b) AMCAB with β =8.3 mm−1 ,γ1=5.5 mm−1 and γ2=0.1 mm−1.

调制后AMCAB 的焦距变化可以由下式来表征:

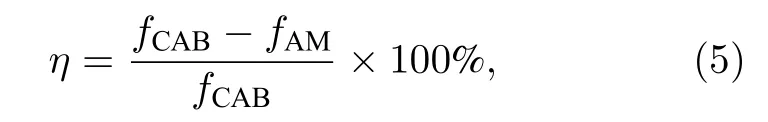
式中,fAM表示调制后AMCAB 的焦距,fCAB表示CAB 的焦距,由于本文不改变CAB 的原始参数,因此fCAB为常数保持不变,不同调制参数的相对焦距差如图4 所示.图4 的结果由遍历法逐点计算获得,从图中可以看到,随着β值的不断增大,AMCAB的焦距在递增,类似的,增大γ2也可以使AMCAB的焦距明显增大,这说明增加频谱中的高频分量将使得光束趋向于聚焦在更远的地方.γ1的变化对AMCAB 的焦距影响则相对较小,说明频谱中的低频分量对焦距的影响较小,这一结论可以解释为什么文献[17]中CAB 经过高通滤波后,光束的焦距能保持不变.

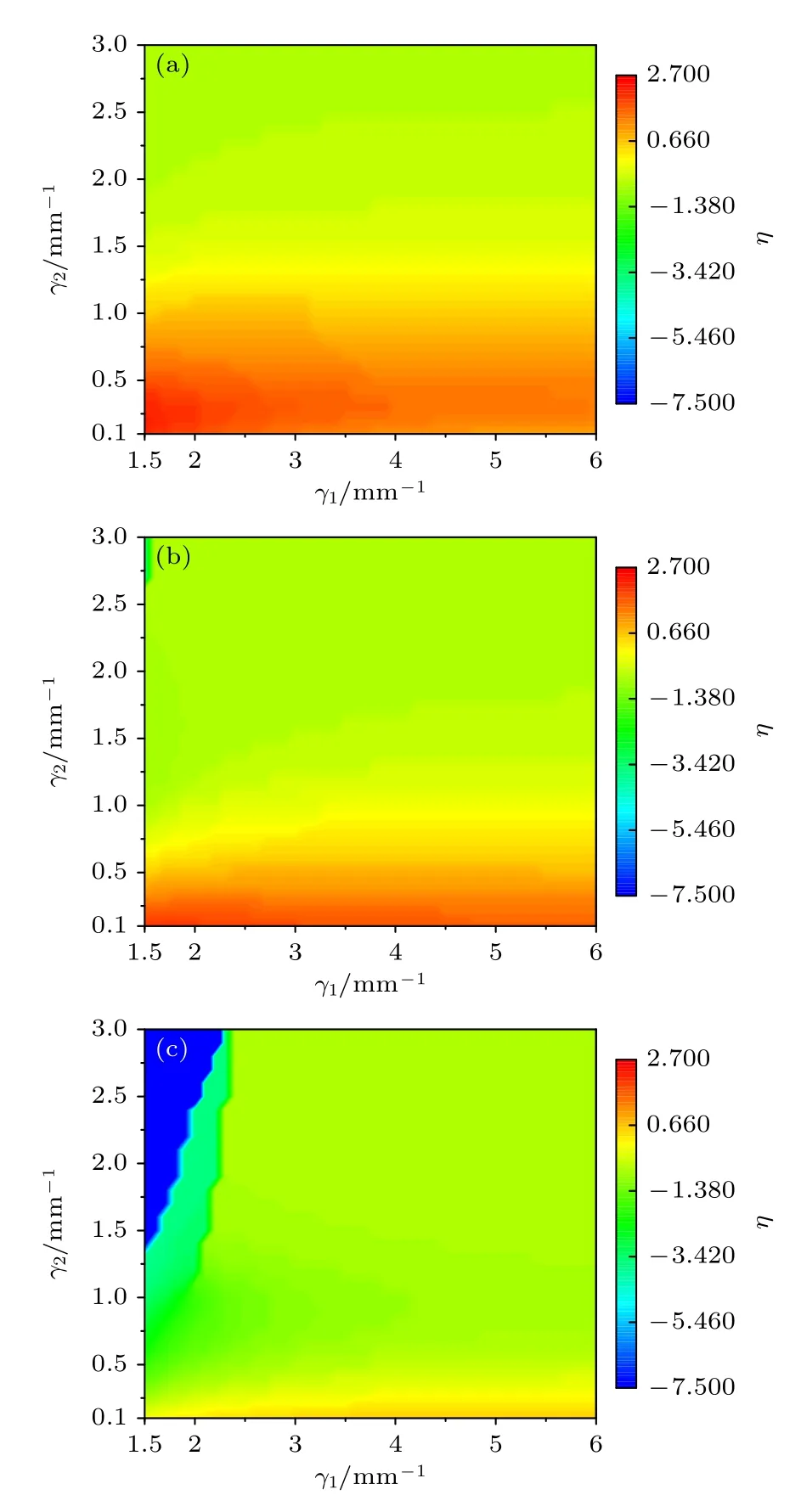
图4 β 不同时,AMCAB 和CAB 的相对焦距差 η 随 γ1,γ2 的变化情况 (a) β =6 mm−1 ;(b) β =7 mm−1 ;(c)β=8 mm−1Fig.4.The relative focal distance difference between the CAB and the AMCAB as a function of γ1 and γ2 with different β.(a) β =6 mm−1 ; (b) β =7 mm−1 ; (c) β=8 mm−1.

在实际应用中,焦点处的光强峰值是影响突然自聚焦光束应用价值的关键参数,图5 给出了调制参数不同时,AMCAB 的焦点峰值与CAB的焦点峰值之比(IAM)max/(ICAB)max,由于不改变CAB的原始参数,因此其中 (ICAB)max为常数保持不变.图5的结果由遍历法逐点计算获得,从图中可以看到,当β较小时,需要γ2较大才能获得较大的光强比值,如图5(a)所示,这是由于此时频谱的中心频段频率较低,因此需要增加较多的高频分量才能起到较好的调制效果.但持续增加γ2并不能使光强比值一直增大,当γ2超过某一阈值后,光强比值开始减小.图5 的中虚线为光强比值的极大值位置随γ1和γ2的变化曲线,可以清楚的看到,虚线随着β的增大快速向γ2减小的方向移动,表明γ2的阈值会随着β的增大急剧减小,因此在频谱中一直增加高频分量的比重并不能持续改善光束的聚焦能力,当高频分量过多时反而会起到反效果.另一方面,当β较小时,γ1对光强比值的影响很小,如图5(a)所示,这是由于此时频谱的中心频率较低,频谱整体处于低频,因此即使γ1很小,频谱中也不缺乏低频分量.但随着β的增大,γ1对光强比值的影响逐渐显现,此时需要γ1较大,才能获得较大的光强比值,如图5(d)所示.这说明低频分量对光束的自聚焦性能同样起着不可或缺的作用,单纯的滤除低频分量虽然对光束的自聚焦能力有一定的改善作用,但并不能获得最佳的调制效果,而是需要高、低频分量达到一个合适的配比.因此采用非对称包络调制的方法比高通滤波[17]和对称包络调制[21]更合理,经过仿真计算比较后,发现当调制参数的值分别为β=8.3 mm−1、γ1=5.5 mm−1、γ2=0.1 mm−1时,光强比达到最大值3.4,比GCAB 的最佳结果[21](光强比最大值2.9)提升了17%.

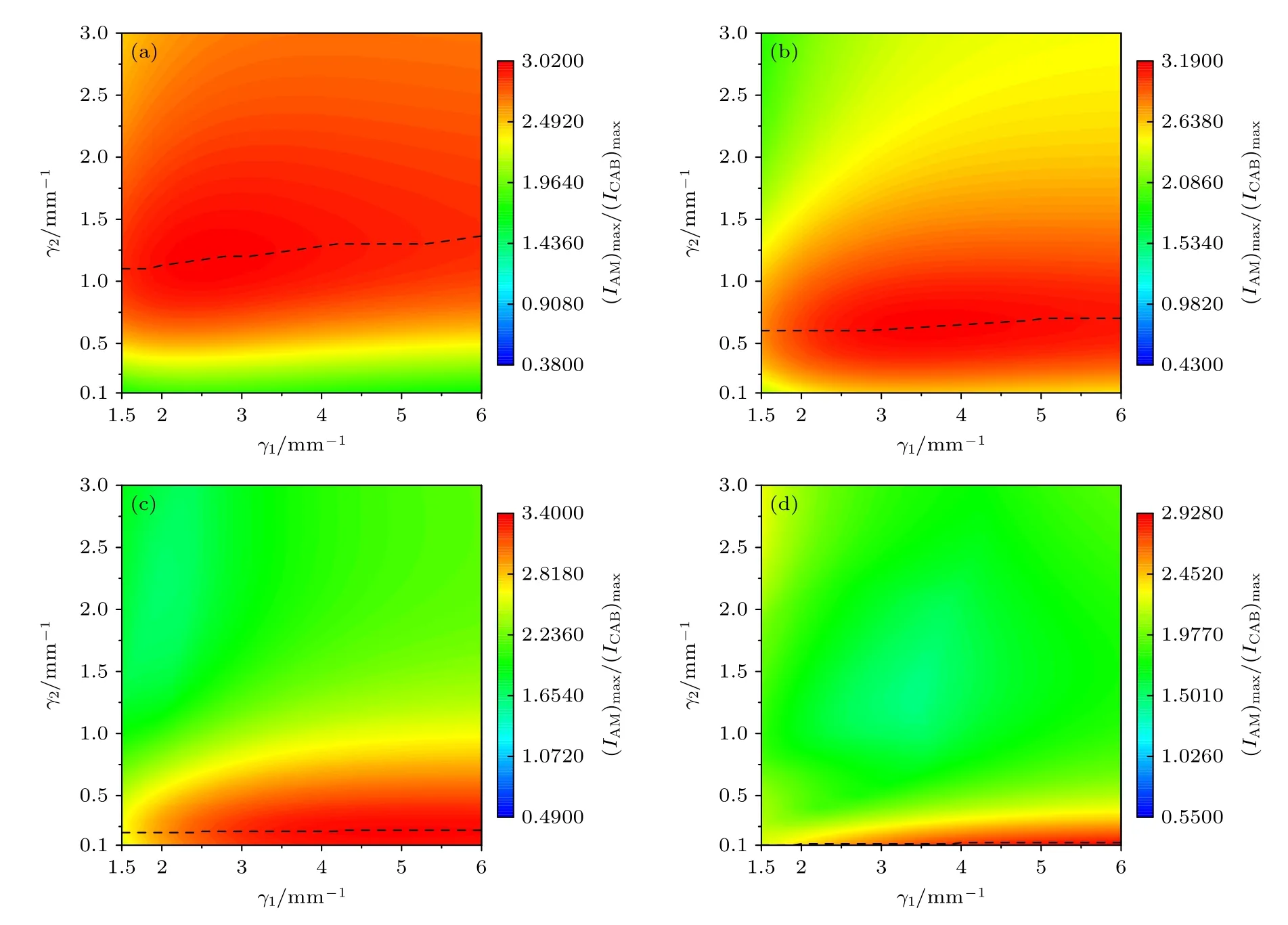
图5 β 不同时,AMCAB 和CAB 的焦点光强比值随 γ1 ,γ2 的变化情况,其中虚线为光强比值的极大值位置随 γ1 和 γ2 的变化曲线 (a) β =6 mm−1 ;(b) β =7 mm−1 ;(c) β =8 mm−1 ;(d) β=9 mm−1Fig.5.The maximum focal intensity contrast between the AMCAB and the CAB as a function of γ1 and γ2 with different β.Here,the dash lines show the positions of the maximum values as a function of γ1 and γ2.(a) β =6 mm−1 ;(b) β =7 mm−1 ;(c) β=8 mm−1 ;(d) β =9 mm−1.

焦斑尺寸是研究者关注的另一个问题,图6 给出了不同参数的AMCAB 的焦点光强分布,为了便于比较,图6 作了归一化处理.从图中可以看到,焦斑的半高全宽(full width at half maximum,FWHM)随着β增大而显著减小.在β不变的条件下,增大γ1会 使得焦斑略微增大;反之,增大γ2会使得焦斑略微减小.这说明包络后频谱的中心频率是影响焦斑大小的主要因素,在中心频率确定的条件下,频谱中低频与高频组分的比重对焦斑尺寸影响相对较小.

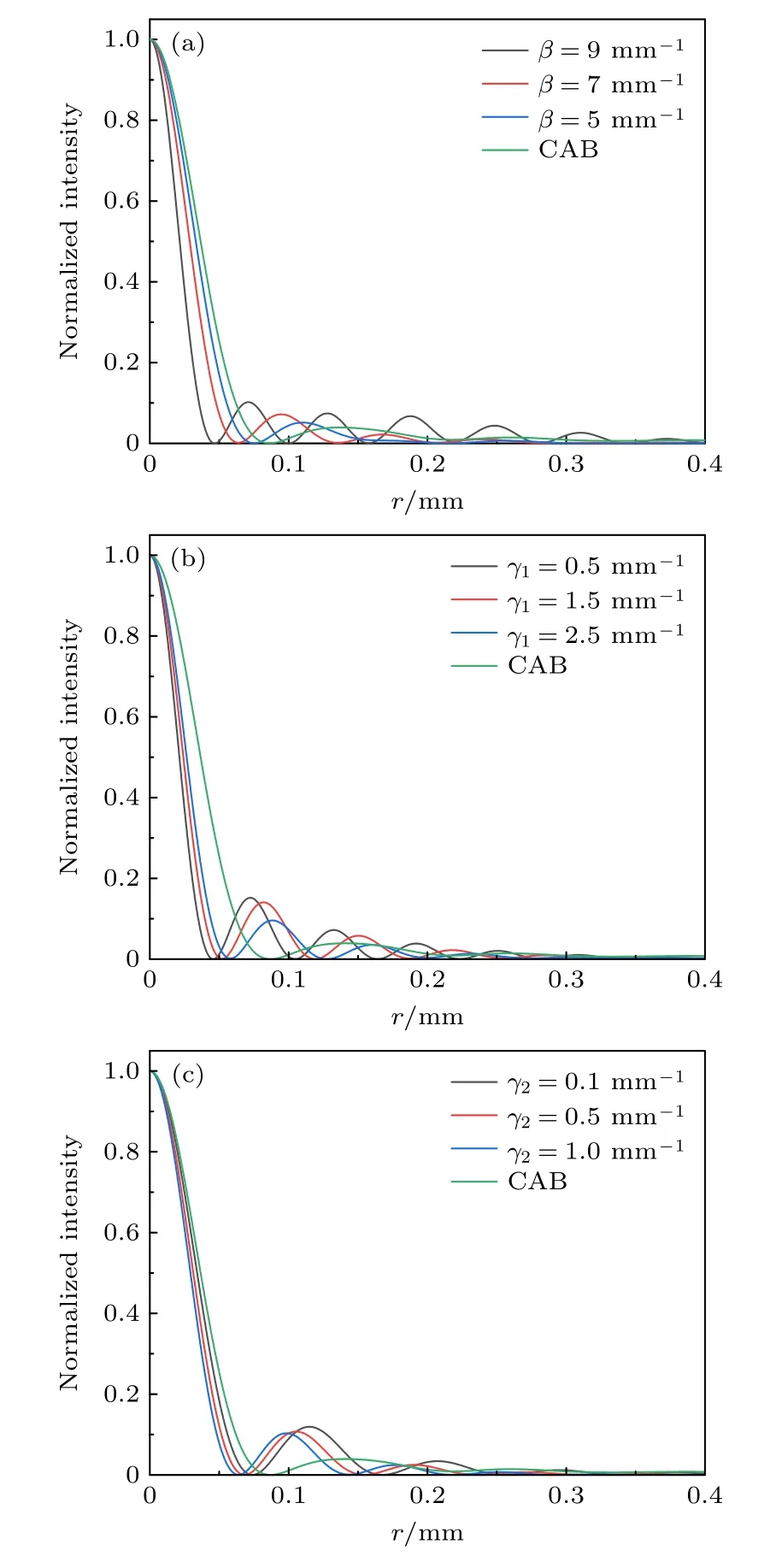
图6 不同参数的AMCAB 在焦平面上的归一化光强分布 (a) γ1=3 mm−1 ,γ2=1.5 mm−1 时,不同 β 的AMCAB;(b) β =7 mm−1,γ2=1 mm−1 时,不同 γ1 的AMCAB;(c) β =6 mm−1,γ1=1 mm−1 时,不同 γ2 的AMCAB.Fig.6.Normalized intensity distributions of AMCAB with different parameters at the focal plane:(a) AMCAB with different β when γ1=3 mm−1,γ2=1.5 mm−1 ;(b) AMCAB with different γ1 when β =7 mm−1 ,γ2=1 mm−1 ;(c) AMCAB with different γ2 when β =6 mm−1,γ1=1 mm−1.

CAB 的突然自聚焦特性可以用光强对比度IC=Imax(z)/Imax(0) 来衡量[6],其中Imax(z) 是光束传播过程中任意截面的最大光强,Imax(0) 是初始面最大光强.图7 给出了不同参数的AMCAB 沿z轴的IC分布结果,同时给了CAB 的结果便于比较.与CAB 类似,AMCAB 在自聚焦前都能保持极低的光强分布,在焦点处光强突然增强,表现出极强的突然自聚焦特性.未调制前,CAB 焦点处的光强峰值约为初始面的52 倍,即焦点处IC≈52,而经调制后AMCAB 的焦点处IC提升为几百乃至一千多倍,突然自聚焦能力得到大幅提升.这是因为与CAB 相比,一方面,AMCAB 的自聚焦能力增强,焦点光强峰值增大;而更重要的是,由于调制后中心频率的后移,初始面最大光强急剧减小,使得光强比值IC突增.从图中可以看到,焦点处IC受β和γ2的影响较大,随着β和γ2的 增大而增大,而受γ1的影响较小.这是因为初始面最大光强受β和γ2的影响较大,随着β和γ2的增大,其值持续减小,如图2(b)和图2(f)所示.

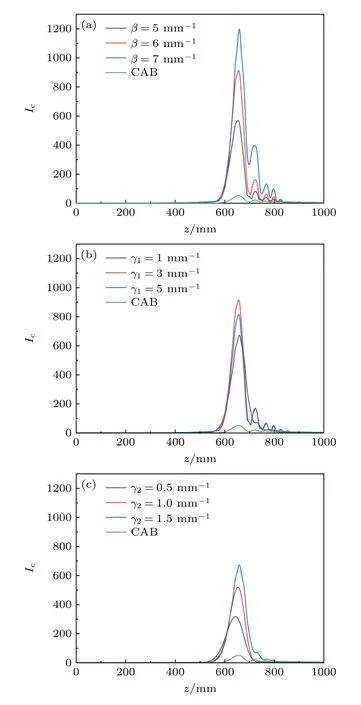
图7 不同参数的AMCAB 沿z 轴的 IC 分布仿真结果(a) γ1=3 mm−1 ,γ2=1.5 mm−1 时,不同 β 的AMCAB;(b) β =6 mm−1,γ2=1.5 mm−1 时,不 同 γ1 的AMCAB;(c) β =6 mm−1,γ1=1 mm−1 时,不同 γ2 的AMCAB.Fig.7.Simulated results of on-axis intensity contrast IC of AMCAB with different parameters.(a) AMCAB with different β when γ1=3 mm−1 ,γ2=1.5 mm−1 ;(b) AMCAB with different γ1 when β =6 mm−1,γ2=1.5 mm−1 ;(c) AMCAB with different γ2 when β =6 mm−1,γ1=1 mm−1.

从上述分析讨论可知,通过增大β,即增高中心频率的方法,可以获得更小的焦斑和更强的突然自聚焦性,但过大的β会使得焦点峰值光强减小,且使得初始面的光环分布过密,增加实验实现的难度.因此综合考虑,调制参数取β=8.3 mm−1,γ1=5.5 mm−1,γ2=0.1 mm−1时为最佳选择,表1 给出了在此参数下的调制结果,并同时列出了CAB 和对称包络的GCAB[21]最佳结果进行比较.从表中可以看到,相比对称包络,采用非对称包络调制使得各项指标都得到了较大幅度的提升,证明非对称包络调制的方法要明显优于对称包络调制.

表1 CAB 与GCAB,AMCAB 最佳调制结果的比较Table 1.The optimized results of GCAB and AMCAB,and the results of CAB are also presented for comparison.

3 实验结果

目前,研究者通常使用傅里叶变换法方法[9,21]来产生CAB,这种方法可以获得所需特定参数的光束,且光路简单,如图8 所示.AMCAB 基于频谱调制,因此可以使用相同的方法来产生,易于实验实现也是本方法的优点之一.本文使用了波长为632.8 nm 的氦氖激光器作为光源,光束经过半波片将偏振方向调整到与空间光调制器(SLM,Holoeye PLUTO-2)的工作方向平行,然后经透镜组与小孔整形扩束后入射到SLM 上.SLM 用于加载经相位编码后的频谱信息,位于一焦距为300 mm的傅里叶透镜的前焦面上,光束经SLM 反射后通过傅里叶透镜进行傅里叶变换.挡板位于傅里叶透镜的后焦面上,为一直径约1 mm 的不透明圆斑,用来遮挡光轴上的零级衍射光.光束在挡板后产生AMCAB,如图中虚线A位置所示.CCD 可沿光轴移动,用以记录AMCAB 在不同传播位置上的光强分布.虚线B和虚线C分别给出了AMCAB传播到400 mm 和焦点处的位置图示.

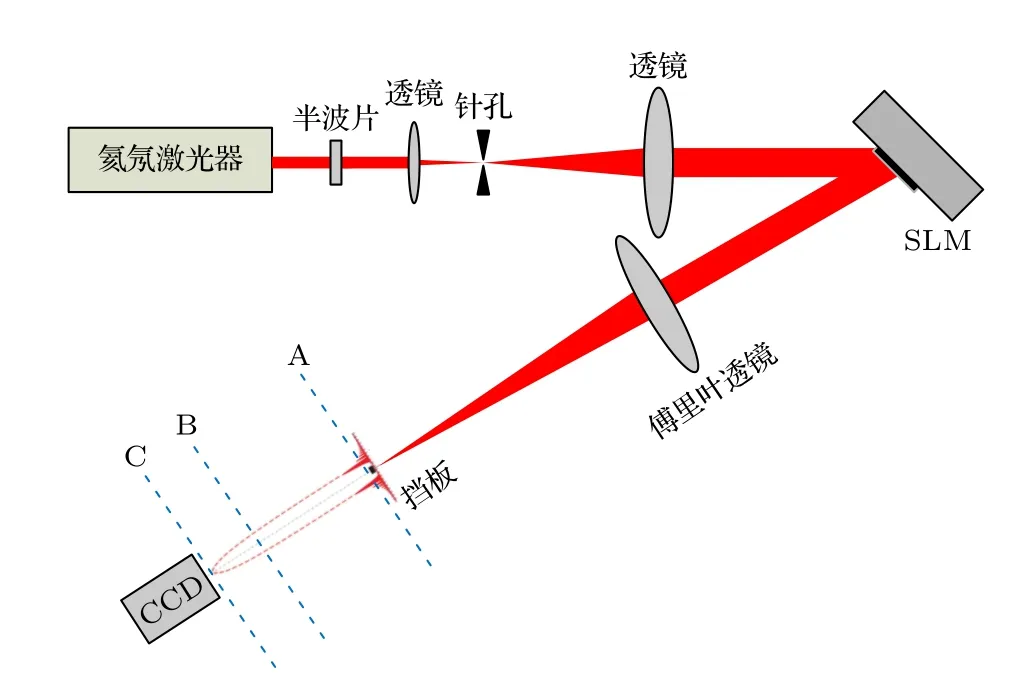
图8 实验光路示意图Fig.8.Diagram of experimental setup.

图9 给出了CAB 和不同调制参数的AMCAB在初始面的光强分布实验结果,以及各自相应的加载于SLM 上的相位分布图,测量位置如图8 中虚线A所示,为了便于比较,图中同时给出了相应的理论仿真结果并对光强最大值作了归一化处理.从图中可以看到,实验结果与理论仿真结果吻合得很好,证明非对称双曲正割包络确实能够有效地对CAB 的频谱进行调控,从而改变其初始面的光强分布.

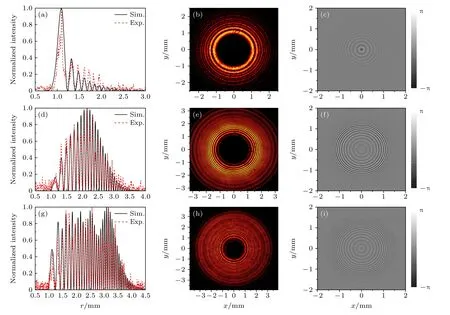
图9 初始面光强分布的实验(虚线)和仿真(实线)结果以及相应的加载于SLM 上的相位分布图 (a) CAB 的归一化径向光强分布和(b)二维光强分布实验结果以及(c)SLM 上加载的相位分布;(d) β =6 mm−1,γ1=2.3 mm−1 ,γ2=0.8 mm−1 时,AMCAB的归一化径向光强分布和(e)二维光强分布实验结果以及(f)SLM 上加载的相位分布;(g) β =8.3 mm−1 ,γ1=5.5 mm−1,γ2=0.1 mm−1时,AMCAB 的归一化径向光强分布和(h)二维光强分布实验结果以及(i) SLM 上加载的相位分布Fig.9.Phase masks on the SLM,experimental (dash line) and simulated (solid line) results of normalized intensity distributions profiles at initial plane:(a) Radial intensity distributions and (b) measured 2D intensity distributions of CAB,and (c) corresponding phase mask on the SLM;(d) radial intensity distributions and (e) measured 2D intensity distributions of AMCAB with β=6 mm−1 ,γ1=2.3 mm−1,γ2=0.8 mm−1,and (f) corresponding phase mask on the SLM;(g) radial intensity distributions and (h) measured 2D intensity distributions of AMCAB with β =8.3 mm−1 ,γ1=5.5 mm−1 ,γ2=0.1 mm−1,and (i) corresponding phase mask on the SLM.

为了进一步实验验证AMCAB 的传播特性,图10 给出了参数为β=8.3 mm−1,γ1=5.5 mm−1,γ2=0.1 mm−1的AMCAB 在z=400 mm (测量位置如图8 中虚线B 所示)和焦平面处(z=655 mm,测量位置如图8 中虚线C所示)的光强分布,其中Imax(0)为初始面光强峰值.从图中可以看到,调制后的AMCAB 在传播过程中仍然能保持很低的光强峰值,即使在比较靠近焦平面的400 mm 处,光强峰值才达到初始面光强峰值的3.2 倍.而在到达焦平面时,实验光强峰值由于实验误差略小于仿真结果,但光强峰值比值也达到了1300 倍,表明AMCAB 具有极强的突然自聚焦特性,与理论预期相一致.实验结果与理论计算结果不完全相符的原因主要有两个,1)数值计算的相位全息算法本身并不能完全精确地还原被编码的频谱信息,引入了计算误差;2)实验过程中不可避免的引入了实验误差,最终使得实验所得的光束与理论结果出现了微小的偏差.

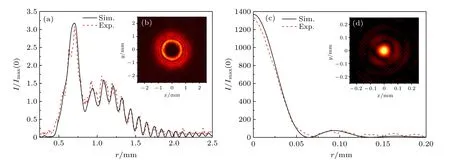
图10 参数 β =8.3 mm−1 ,γ1=5.5 mm−1 ,γ2=0.1 mm−1 时,AMCAB 在不同截面光强分布的实验(虚线)和仿真(实线)结果,其中 Imax(0) 为初始面光强峰值 (a) z =400 mm 处的径向光强比值分布和相应的(b)二维光强分布实验结果;(c)焦平面(z =655 mm)处的径向光强比值分布和相应的(d)二维光强分布实验结果Fig.10.Experimental (dash line) and simulated (solid line) results of intensity contrast I /Imax(0) of AMCAB with β =8.3 mm−1,γ1=5.5 mm−1,γ2=0.1 mm−1 at different propagation planes:(a) Radial intensity contrast and (b) corresponding measured 2D intensity distributions at z =400 mm ;(c) radial intensity contrast and (d) the corresponding measured 2D intensity distributions at the focal plane (z =655 mm).

4 结论

本文理论和实验研究了AMCAB 的自聚焦特性,发现通过改变3 个调制参数β,γ1和γ2的取值,可以调节AMCAB 的自聚焦特性,如焦距、焦斑尺寸、焦点光强等.通过增加频谱中的高频分量,可使得AMCAB 的焦距变大,而低频分量的变化对其焦距影响则较小.持续增加频谱中高频分量的比重,可以在焦点处获得更小的焦斑半径和更高的光强对比度,但过多的高频分量会使得焦点光强峰值减小,这说明为了获得最佳的自聚焦性能,低频分量也不可或缺.相比于使用对称包络调制的GCAB,非对称包络调制使得AMCAB 可以灵活地改变调制后频谱中高频与低频组分的占比,充分发挥了频谱包络调制方法的优点,因此调制效果显著优于GCAB 的结果.最后,对理论分析结果进行了实验验证,实验结果与理论结果吻合得很好,证明频谱的非对称包络调制是一种高效且易于实现的调制方法.